スポンサーリンク
交流回路の電力の計算(抵抗だけの回路)
※ページ内にPR・広告が含まれる場合があります。
正弦波交流電源に抵抗だけ接続されている次のような回路において、
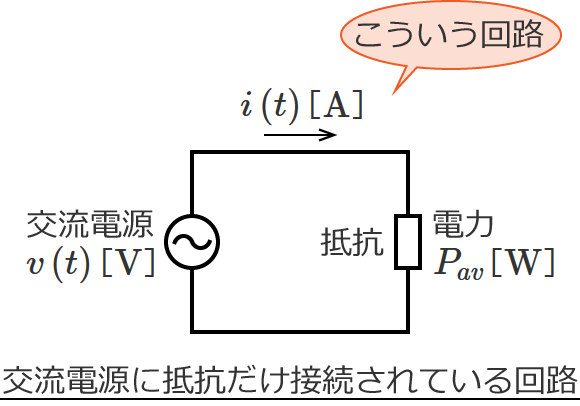
この回路の電力(平均電力)$P_{av}$ を、電圧の瞬時値 $v\left( t\right)$ と電流の瞬時値 $i\left( t\right)$ から求めてみます。
電圧の瞬時値 $v\left( t\right)$ と電流の瞬時値 $i\left( t\right)$ から電力(平均電力)$P_{av}$ を求めるときのざっくりとした計算手順は、次のようになります。
電力(平均電力)を求める計算手順
電圧の瞬時値と電流の瞬時値をかけて電力の瞬時値を求める
求めた電力の瞬時値を1周期の範囲で積分して平均する
手順はこれだけなのですが、計算の過程で三角関数の公式や積分を使ったりするので、途中の計算がちょっと大変だったりします。
積分を使わなくても電力(平均電力)を求めることはできます。詳細はページ下に記載の補足を参照してみてください。
では、電圧の瞬時値 $v\left( t\right)$ と電流の瞬時値 $i\left( t\right)$ から電力(平均電力)$P_{av}$ を計算してみます。
スポンサーリンク
負荷が抵抗だけの場合の交流回路の電力(平均電力)の計算
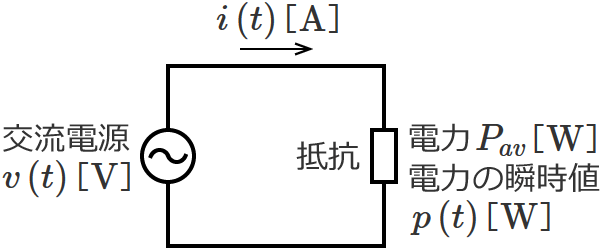
抵抗に接続されている正弦波交流電源の電圧の最大値を $V_m$[$\mathrm{V}$]、角周波数を $\omega$[$\mathrm{rad/s}$]、時間を $t$[$\mathrm{s}$]とすると、抵抗にかかる電圧の瞬時値 $v\left( t\right)$[$\mathrm{V}$]は、
$v\left( t\right) =V_m\sin\omega t$ [$\mathrm{V}$] …①
と表わせます。
またこのとき、負荷は抵抗だけ(つまり、電圧と電流に位相差がない)なので、抵抗に流れる電流の最大値を $I_m$[$\mathrm{A}$]とすると抵抗に流れる電流の瞬時値 $i\left( t\right)$[$\mathrm{A}$]は、
$i\left( t\right) =I_m\sin\omega t$ [$\mathrm{A}$] …②
と表わせます。
①は電圧の瞬時値 $v\left( t\right)$ 、②は電流の瞬時値 $i\left( t\right)$ なので、①と②をかけて電力の瞬時値 $p\left( t\right)$ は、
$p\left( t\right) =v\left( t\right)\times i\left( t\right)$ $=V_m\sin\omega t\times I_m\sin\omega t$ $=V_mI_m\sin^2\omega t$
$\therefore p\left( t\right) =V_mI_m\sin^2 \omega t$ …③
ここで、三角関数の公式(倍角の公式:$\cos 2\alpha =1-2\sin^2\alpha$ より、$\sin^2\alpha=\dfrac{1-\cos 2\alpha}{2}$ )を使うと③式は、
$p\left( t\right) =V_mI_m\sin^2 \omega t$ $=V_mI_m\dfrac{1-\cos 2\omega t}{2}$ $=\dfrac{V_mI_m}{2}\left( 1-\cos 2\omega t\right)$
$\therefore p\left( t\right) =\dfrac{V_mI_m}{2}\left( 1-\cos 2\omega t\right)$ [$\mathrm{W}$] …④ ($\Leftarrow$ 電力の瞬時値 $p\left( t\right)$ の式)
となり、この④式が電力の瞬時値 $p\left( t\right)$ の式になります。ちなみに、この④式の $p\left( t\right)$ を瞬時電力といいます。
電力の瞬時値 $p\left( t\right)$ が求められたので、次に、④式を1周期の範囲で積分して平均し、電力(平均電力)$P_{av}$ を求めます。電力(平均電力)$P_{av}$ は、
$P_{av}=\dfrac{1}{\frac{T}{2}}\displaystyle\int_0^\frac{T}{2} p\left( t\right)\, dt$ $=\dfrac{1}{\frac{T}{2}}\displaystyle\int_0^\frac{T}{2} \dfrac{V_mI_m}{2}\left( 1-\cos 2\omega t\right)\, dt$ …⑤
$v\left( t\right)$(または $i\left( t\right)$ )の周期を $T$ とすると、$p\left( t\right)$ の周期は $T/2$ になります。
ここで、$T=\dfrac{1}{f}=\dfrac{2\pi}{\omega}$( $\because \omega =2\pi f$ )より、$\dfrac{T}{2} =\dfrac{\pi}{\omega}$ なので、これを⑤式に代入すると、
$P_{av}=\dfrac{1}{\frac{\pi}{\omega}}\displaystyle\int_0^\frac{\pi}{\omega}\dfrac{V_mI_m}{2}\left( 1-\cos 2\omega t\right)\, dt$ …⑥
あとは、この⑥式を計算していきます。$\dfrac{V_mI_m}{2}$ は定数なので、積分の外に出します。
$P_{av}=\dfrac{1}{\frac{\pi}{\omega}}\cdot\dfrac{V_mI_m}{2}\displaystyle\int_0^\frac{\pi}{\omega}\left( 1-\cos 2\omega t\right)\, dt$
$=\dfrac{\omega V_mI_m}{2\pi}\displaystyle\int_0^\frac{\pi}{\omega}\left( 1-\cos 2\omega t\right)\, dt$
$=\dfrac{\omega V_mI_m}{2\pi}\left[ t-\dfrac{\sin 2\omega t}{2\omega}\right]_0^\frac{\pi}{\omega}$ ( $\because \displaystyle\int 1\, dt=t+C$、$\displaystyle\int\cos 2\omega t\, dt=\dfrac{\sin 2\omega t}{2\omega} +C$ )
$=\dfrac{\omega V_mI_m}{2\pi}\left\{\left(\dfrac{\pi}{\omega} -\dfrac{\sin\left( 2\omega\cdot\dfrac{\pi}{\omega}\right)}{2\omega}\right) -\left( 0-\dfrac{\sin\left( 2\omega\cdot 0\right)}{2\omega}\right)\right\}$
$=\dfrac{\omega V_mI_m}{2\pi}\left\{\left(\dfrac{\pi}{\omega} -\dfrac{\sin 2\pi}{2\omega}\right) -\left( -\dfrac{\sin 0}{2\omega}\right)\right\}$
$=\dfrac{\omega V_mI_m}{2\pi}\left\{\left(\dfrac{\pi}{\omega} -0\right) -\left( -0\right)\right\}$
$=\dfrac{\omega V_mI_m}{2\pi}\cdot\dfrac{\pi}{\omega} =\dfrac{V_mI_m}{2}$
$\therefore P_{av}=\dfrac{V_mI_m}{2}$ [$\mathrm{W}$] …⑦ ($\Leftarrow$ 電力(平均電力)$P_{av}$ の式)
となります。
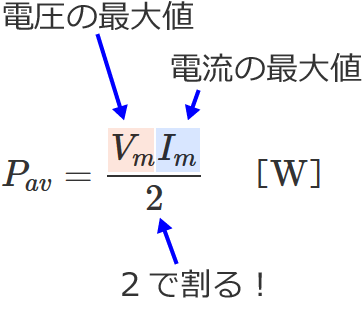
この⑦式が抵抗だけ接続されている場合の電力(平均電力)になり、抵抗だけ接続されている場合の電力(平均電力)$P_{av}$ は、
電圧の最大値 $V_m$ と電流の最大値 $I_m$ をかけて2で割った値
になります。
⑦式の電力の式についてもうちょっと考えてみる
ここで、⑦式についてもうちょっと考えてみます。
正弦波交流回路では、電圧の実効値を $V_r$ 、電流の実効値を $I_r$ とすると、
電圧の最大値 $V_m=\sqrt{2}\, V_r$ …⑧
電流の最大値 $I_m=\sqrt{2}\, I_r$ …⑨
と表わせるのでした。
なので、これら⑧と⑨を⑦式に代入してみると、
$P_{av}=\dfrac{V_mI_m}{2}=\dfrac{\sqrt{2}\, V_r\times\sqrt{2}\, I_r}{2}$ $=\dfrac{2\, V_rI_r}{2}$ $=V_rI_r$
$\therefore P_{av}=V_rI_r$ [$\mathrm{W}$]
となり、電圧と電流をかけただけのよく見る電力の式になります。(ただし、この式の電圧と電流は実効値ですよ。)
つまり、電圧と電流の最大値で電力を表わすならば、
$P_{av}=\dfrac{V_mI_m}{2}$ [$\mathrm{W}$]
電圧と電流の実効値で電力を表わすならば、
$P_{av}=V_rI_r$ [$\mathrm{W}$]
になるよ、ということです。

スポンサーリンク
スポンサーリンク
負荷が抵抗だけの場合の交流回路の電力の波形
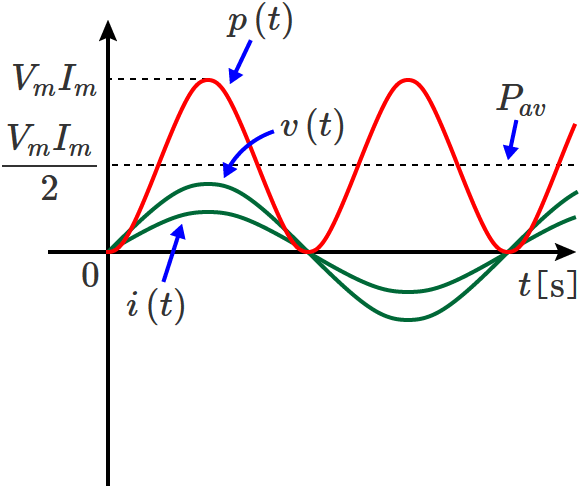
電圧 $v\left( t\right)$ 、電流 $i\left( t\right)$ 、電力 $p\left( t\right)$ の波形を書いてみると、次のようになります。
電圧と電流の波形
負荷が抵抗だけの回路なので、電圧 $v\left( t\right)$ と電流 $i\left( t\right)$ の波形は、位相のズレがない波形(時間的にズレていない波形)になります。
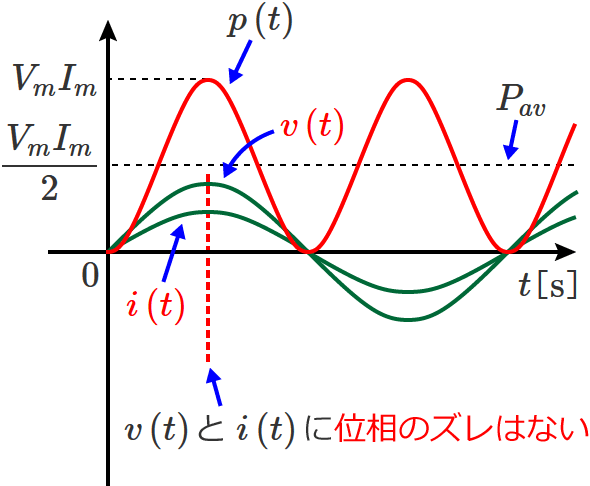
電力の波形
電力 $p\left( t\right)$ の波形は電力(平均電力)$P_{av}$ の値 $\dfrac{V_mI_m}{2}$ を中心として最大値が $V_mI_m$ 、最小値がゼロの正弦波状の波形になり、電力 $p\left( t\right)$ の周波数は電圧 $v\left( t\right)$(または電流 $i\left( t\right)$ )の周波数の2倍になります。
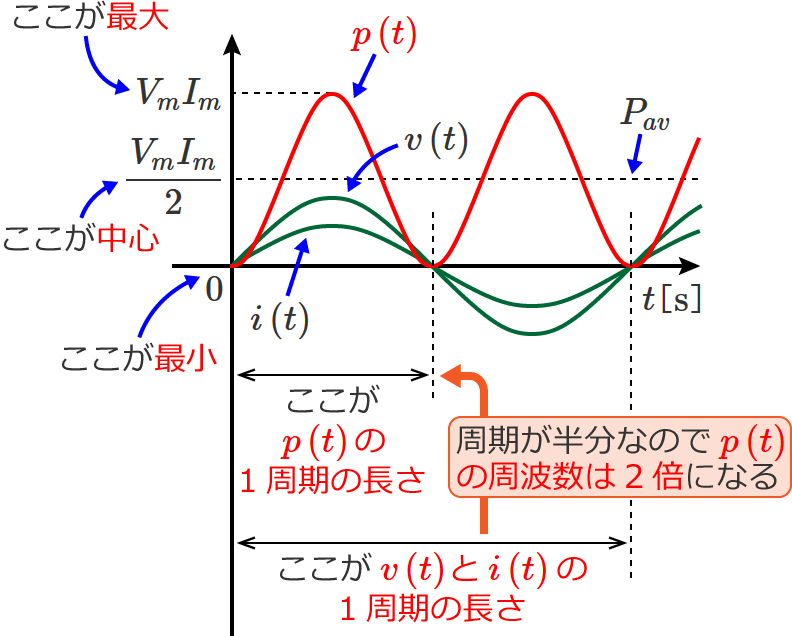
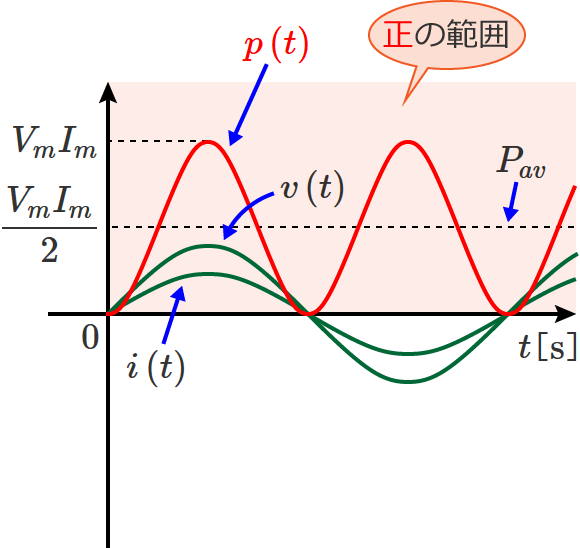
また、波形から分かるように、負荷が抵抗だけの回路の場合、電力の瞬時値 $p\left( t\right)$ は常に正の値になります。
電力 $p\left( t\right)$ の周波数は電圧 $v\left( t\right)$ の周波数の2倍になる
電圧の瞬時値 $v\left( t\right)$ の式は、$v\left( t\right) =V_m\sin\omega t$ です。
一方、電力の瞬時値 $p\left( t\right)$ の式は、$p\left( t\right) =\dfrac{V_mI_m}{2}\left( 1-\cos 2\omega t\right)$ です。
2つの式の $\sin$ と $\cos$ の中を見比べてみると、
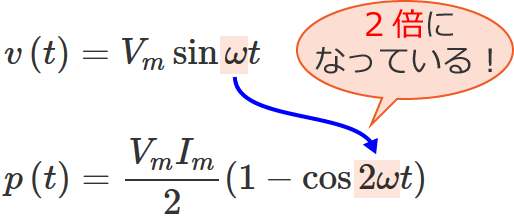
となっているので、電力 $p\left( t\right)$ の周波数は電圧 $v\left( t\right)$ の周波数の2倍になります。
なお、周波数が2倍になるということは、$T=\dfrac{1}{f}$ の関係から周期は半分(1/2倍)になることになります。
積分を使わないで電力(平均電力)$P_{av}$ を求める方法(その1)
このページでは、電力の瞬時値 $p\left( t\right)$ から電力(平均電力)$P_{av}$ を求めるときに積分を使いましたが、積分を使わなくても電力(平均電力)を求めることができます。
電力の瞬時値 $p\left( t\right)$ の式は、$p\left( t\right) =\dfrac{V_mI_m}{2}\left( 1-\cos 2\omega t\right)$ なので、これを次のように変形(展開)します。
$p\left( t\right) =\dfrac{V_mI_m}{2} -\dfrac{V_mI_m}{2}\cos 2\omega t$ …⑩
すると、⑩式の右辺の第2項は定数 $\dfrac{V_mI_m}{2}$ に $\cos 2\omega t$ をかけたものなので、第2項は平均するとゼロになる式になっています。(第1項は定数なので、平均しても同じ値 $\dfrac{V_mI_m}{2}$ になります。)
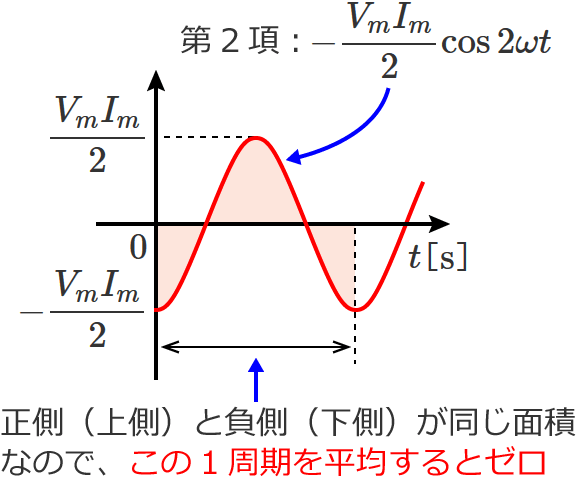
なので、第2項をゼロとすれば電力(平均電力)$P_{av}$ が求められ、 $\therefore P_{av}=\dfrac{V_mI_m}{2}$ となります。
積分を使わないで電力(平均電力)$P_{av}$ を求める方法(その2)
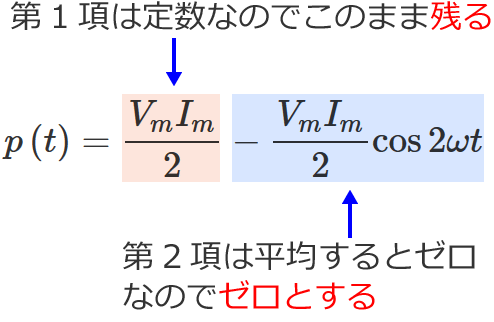
電力の瞬時値 $p\left( t\right)$ の波形のグラフが書ければ、その波形のグラフから電力(平均電力)$P_{av}$ が分かります。
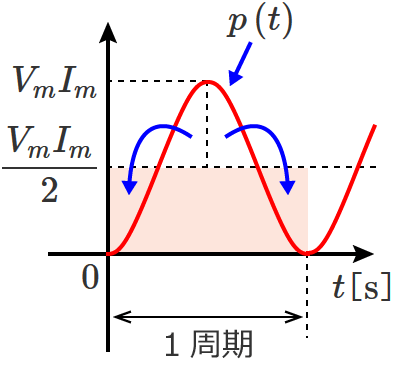
上の図の矢印のように $p\left( t\right)$ の上側の部分それぞれを左下と右下に移動すると、平均が $\dfrac{V_mI_m}{2}$ になることが分かる。
$\therefore P_{av}=\dfrac{V_mI_m}{2}$
- 電力の瞬時値: $p\left( t\right) =\dfrac{V_mI_m}{2}\left( 1-\cos 2\omega t\right)$ [$\mathrm{W}$]
- 電力(平均電力): $P_{av}=\dfrac{V_mI_m}{2}$ [$\mathrm{W}$]
- 電力の瞬時値(瞬時電力)$p\left( t\right)$ の周波数は、電圧 $v\left( t\right)$ の周波数の2倍になる(周期は1/2倍)
スポンサーリンク
スポンサーリンク
他の回路についても電力(平均電力)の計算をしていますので、それぞれ次のページを参考にしてみてください。
コイルだけの回路はこちら ⇒ 交流回路の電力の計算(コイルだけの回路)
コンデンサだけの回路はこちら ⇒ 交流回路の電力の計算(コンデンサだけの回路)
RL直列回路はこちら ⇒ 交流回路の電力の計算(RL直列回路)
RC直列回路はこちら ⇒ 交流回路の電力の計算(RC直列回路)
抵抗だけの回路の電圧と電流の計算とベクトル図については、こちらの交流回路の電圧と電流の計算とベクトル図(抵抗だけの回路)のページを参考にしてみてください。
位相と位相差については、こちらの交流回路の位相のページを参考にしてみてください。
RLC直列回路の電圧と電流の計算(電源の電圧を基準にした場合) ←BACK
NEXT→ 交流回路の電力の計算(コイルだけの回路)
スポンサーリンク
交流回路の電力の計算(抵抗だけの回路) 関連ページ
- インピーダンス
- インピーダンスについて解説しています。交流回路での電圧と電流の比をインピーダンスといい、インピーダンスの大きさは、交流電流の流れにくさを表わします。インピーダンスの求め方や、インピーダンス三角形、インピーダンス角などについても解説していますので参考にしてみてください。
- 複素インピーダンス
- 複素インピーダンスについて解説しています。複素数で表わされたインピーダンスを複素インピーダンスといい、複素インピーダンスの実部は抵抗、虚部はリアクタンスを表わします。いろいろな交流回路の複素インピーダンスの求め方などについても解説していますので参考にしてみてください。
- アドミタンス
- アドミタンスについて解説しています。インピーダンスの逆数をアドミタンスといい、アドミタンスの大きさは、交流電流の流れやすさを表わします。アドミタンスの求め方や、アドミタンス三角形、アドミタンス角などについても解説していますので参考にしてみてください。
- 複素アドミタンス
- 複素アドミタンスについて解説しています。複素数で表わされたアドミタンスを複素アドミタンスといい、複素アドミタンスの実部はコンダクタンス、虚部はサセプタンスを表わします。いろいろな交流回路の複素アドミタンスの求め方などについても解説していますので参考にしてみてください。
- 交流回路のインピーダンスの計算(素子が1個の場合)
- 素子(抵抗R、コイルL、コンデンサC)が1個の場合のインピーダンスについて解説しています。素子(R、L、C)が1個なので、計算というほどの計算もなく求められますが、とりあえずインピーダンスの計算の基礎なので・・・。
- 交流回路の合成インピーダンスの計算(素子が2個直列接続の場合)
- 素子(抵抗R、コイルL、コンデンサC)が2個直列接続された場合(RL直列回路、RC直列回路,LC直列回路)の合成インピーダンスを計算しています。LC直列回路の場合には、コイルLとコンデンサCのリアクタンスの大きさによって合成インピーダンスのベクトルの向きが変わるので気を付けましょう。
- 交流回路の合成インピーダンスの計算(素子が2個並列接続の場合)
- 素子(抵抗R、コイルL、コンデンサC)が2個並列接続された場合(RL並列回路、RC並列回路,LC並列回路)の合成インピーダンスを計算しています。LC並列回路の場合は、条件によって合成インピーダンスのベクトルの向きが変わるので気を付けましょう。各合成インピーダンスのベクトル図も書いていますので、参考にしてみてください。
- 交流回路の合成インピーダンスの計算(RLC直列回路)
- 素子(抵抗R、コイルL、コンデンサC)が3個直列接続された場合(RLC直列回路)の合成インピーダンスを計算しています。RLC直列回路の場合、コイルLとコンデンサCのリアクタンスの大きさが同じときには合成インピーダンスは抵抗Rだけになります。これはすごく大事なことなのでおぼえておきましょう!
- 交流回路の合成インピーダンスの計算(RLC並列回路)
- 素子(抵抗R、コイルL、コンデンサC)が3個並列接続された場合(RLC並列回路)の合成インピーダンスを計算しています。RLC並列回路の場合、周波数が反共振周波数のときコイルLとコンデンサCの並列回路部分が解放状態と同じになるため、合成インピーダンスは抵抗Rだけになります。
- RLC直列共振回路
- RLC直列共振回路について解説しています。RLC直列共振回路はフィルタ回路など電気で幅広く応用されている回路ですので、共振周波数など基本的なことだけでもおぼえておくようにしましょう。
- RLC並列共振回路
- RLC並列共振回路について解説しています。RLC並列共振回路などの共振回路は電気で幅広く応用されている回路ですので、共振周波数など基本的なことだけでもおぼえておくようにしましょう。
- 正弦波交流波形の実効値はなぜ最大値÷√2か?
- 正弦波交流波形の実効値を求めるときは最大値を√2で割ればいいですが、では、なぜ√2で割れば実効値になるのでしょうか?正弦波交流波形の実効値が最大値÷√2になることを計算で導いてみましたので参考にしてみてください。全波整流波形、半波整流波形、方形波、のこぎり波についても実効値を計算してみました。
- なぜコイルに流れる電流の位相は電圧より90°遅れるのか?
- コイルに流れる電流の位相は電圧よりも90°遅れますが、コイルの場合、なぜ電流が電圧よりも90°遅れ位相になるのかを計算で導いています。
- なぜコンデンサに流れる電流の位相は電圧より90°進むのか?
- コンデンサに流れる電流の位相は電圧よりも90°進みますが、コンデンサの場合、なぜ電流が電圧よりも90°進み位相になるのかを計算で導いています。
- 交流回路の電圧と電流の計算とベクトル図(抵抗だけの回路)
- 正弦波交流電源に抵抗だけ接続されている交流回路の回路に流れる電流と、抵抗にかかる電圧の計算方法について解説しています。電圧と電流のベクトル図の描き方についても解説していますので、交流回路の計算やベクトル図の描き方の参考にしてみてください。
- 交流回路の電圧と電流の計算とベクトル図(コイルだけの回路)
- 正弦波交流電源にコイルだけ接続されている交流回路の回路に流れる電流と、コイルにかかる電圧の計算方法について解説しています。電圧と電流のベクトル図の描き方についても解説していますので、交流回路の計算やベクトル図の描き方の参考にしてみてください。
- 交流回路の電圧と電流の計算とベクトル図(コンデンサだけの回路)
- 正弦波交流電源にコンデンサだけ接続されている交流回路の回路に流れる電流と、コンデンサにかかる電圧の計算方法について解説しています。電圧と電流のベクトル図の描き方についても解説していますので、交流回路の計算やベクトル図の描き方の参考にしてみてください。
- 交流回路の電圧と電流の計算とベクトル図(RL直列回路)
- RL直列回路(交流回路)の各素子にかかる電圧、直列接続全体にかかる電圧、位相差の計算方法について解説しています。RL直列回路の電圧と電流のベクトル図の描き方についても解説していますので、RL直列回路の計算やベクトル図の描き方の参考にしてみてください。
- 交流回路の電圧と電流の計算とベクトル図(RC直列回路)
- RC直列回路(交流回路)の各素子にかかる電圧、直列接続全体にかかる電圧、位相差の計算方法について解説しています。RC直列回路の電圧と電流のベクトル図の描き方についても解説していますので、RC直列回路の計算やベクトル図の描き方の参考にしてみてください。
- 交流回路の電圧と電流の計算とベクトル図(RLC直列回路)
- RLC直列回路(交流回路)の各素子にかかる電圧、直列接続全体にかかる電圧、位相差の計算方法について解説しています。RLC直列回路の電圧と電流のベクトル図の描き方についても解説していますので、RLC直列回路の計算やベクトル図の描き方の参考にしてみてください。
- 交流回路の電圧と電流の計算とベクトル図(RL並列回路)
- RL並列回路(交流回路)の各素子に流れる電流、回路全体に流れる電流、位相差の計算方法について解説しています。RL並列回路の電圧と電流のベクトル図の描き方についても解説していますので、RL並列回路の計算やベクトル図の描き方の参考にしてみてください。
- 交流回路の電圧と電流の計算とベクトル図(RC並列回路)
- RC並列回路(交流回路)の各素子に流れる電流、回路全体に流れる電流、位相差の計算方法について解説しています。RC並列回路の電圧と電流のベクトル図の描き方についても解説していますので、RC並列回路の計算やベクトル図の描き方の参考にしてみてください。
- 交流回路の電圧と電流の計算とベクトル図(LC並列回路)
- LC並列回路(交流回路)の各素子に流れる電流と、回路全体に流れる電流の計算方法について解説しています。LC並列回路の電圧と電流のベクトル図の描き方についても解説していますので、LC並列回路の計算やベクトル図の描き方の参考にしてみてください。
- 交流回路の電圧と電流の計算とベクトル図(RLC並列回路)
- RLC並列回路(交流回路)の各素子に流れる電流、回路全体に流れる電流、位相差の計算方法について解説しています。RLC並列回路の電圧と電流のベクトル図の描き方についても解説していますので、RLC並列回路の計算やベクトル図の描き方の参考にしてみてください。
- RL直列回路の電圧と電流の計算(電源の電圧を基準にした場合)
- RL直列回路の回路に流れる電流と各素子にかかる電圧を電源の電圧を基準にして計算していますので、RL直列回路の電圧と電流の計算方法の参考にしてみてください。
- RC直列回路の電圧と電流の計算(電源の電圧を基準にした場合)
- RC直列回路の回路に流れる電流と各素子にかかる電圧を電源の電圧を基準にして計算していますので、RC直列回路の電圧と電流の計算方法の参考にしてみてください。
- RLC直列回路の電圧と電流の計算(電源の電圧を基準にした場合)
- RLC直列回路の回路に流れる電流と各素子にかかる電圧を電源の電圧を基準にして計算していますので、RLC直列回路の電圧と電流の計算方法の参考にしてみてください。
- 交流回路の電力の計算(コイルだけの回路)
- 負荷がコイルだけの場合の交流回路の電力(瞬時電力、平均電力)の計算方法(求め方)、電力の波形などについて解説しています。
- 交流回路の電力の計算(コンデンサだけの回路)
- 負荷がコンデンサだけの場合の交流回路の電力(瞬時電力、平均電力)の計算方法(求め方)、電力の波形などについて解説しています。
- 交流回路の電力の計算(RL直列回路)
- RL直列回路の電力(瞬時電力、平均電力)の計算方法(求め方)、電力の波形などについて解説しています。
- 交流回路の電力の計算(RC直列回路)
- RC直列回路の電力(瞬時電力、平均電力)の計算方法(求め方)、電力の波形などについて解説しています。
- 有効・無効・皮相電力
- 交流回路には「有効電力」「無効電力」「皮相電力」の3種類の電力があります。それぞれの電力の求め方と、3つの電力の関係について解説しています。
- 力率とは?(力率と電力の関係)
- 交流回路の勉強をしていると「力率」がでてきますが、力率って何でしょうか?力率の式の表し方には色々ありますが、ここでは、力率と皮相電力、有効電力、無効電力の関係とその関係式などについて解説します。
- 力率とは?(力率と位相の関係)
- 交流回路の勉強をしていると「力率(cosΘ)」がでてきますが、力率って何でしょうか?力率の式の表し方には色々ありますが、ここでは、位相と力率の関係について抵抗、コイル、コンデンサの回路を例に解説しています。
- 波形の実効値、平均値、最大値、波形率、波高率の求め方
- 波形は色々ありますが、その波形の特性を表わす値として実効値、平均値、最大値、波形率、波高率などがあります。ここでは、波形の実効値、平均値、最大値、波形率、波高率の定義式、求め方について解説しています。
- 正弦波波形の実効値、平均値、最大値、波形率、波高率の計算方法
- 波形は色々ありますが、その波形の特性を表わす値として実効値、平均値、最大値、波形率、波高率などがあります。ここでは、正弦波波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。
- 全波整流波形の実効値、平均値、最大値、波形率、波高率の計算方法
- 波形は色々ありますが、その波形の特性を表わす値として実効値、平均値、最大値、波形率、波高率などがあります。ここでは、全波整流波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。
- 半波整流波形の実効値、平均値、最大値、波形率、波高率の計算方法
- 半波整流波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。波形の特性を表わす値として実効値、平均値、最大値、波形率、波高率などがありますが、これらは大事な値ですので、求め方、計算方法をおぼえておきましょう。
- 方形波波形の実効値、平均値、最大値、波形率、波高率の計算方法
- 方形波波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。方形波波形の場合、実効値と平均値と最大値が同じ値、波形率と波高率が同じ値になります。ちなみに、方形波と矩形波は同じです。
- のこぎり波波形の実効値、平均値、最大値、波形率、波高率の計算方法
- のこぎり波波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。のこぎり波波形の実効値と平均値を求めるためには、のこぎり波波形の式から考えないといけないので、他の波形よりも計算がちょっと大変です。
- 三相電力の公式はなぜ√3倍なのか?(三相電力の公式の導出)
- 三相電力の公式はP=√3VIcosφで表わされますが、なぜ√3倍になるのか?スター結線の場合とデルタ結線の場合それぞれについて、三相電力の公式を導出してみました。この三相電力の公式は電験三種の「理論」「電力」科目の問題を解くときに度々使われる基本的な公式ですのでおぼえておくようにしましょう。
- スター結線(Y結線)の線間電圧はなぜ相電圧の√3倍になるのか?
- スター結線(Y結線)されている三相交流回路の線間電圧は相電圧の√3倍になりますが、なぜ√3倍になるのか?スター結線のときの線間電圧と相電圧のベクトル図を求め、求めたベクトル図から√3倍になる理由について解説しています。
- デルタスター変換(Δ→Y変換)
- デルタスター変換(Δ→Y変換)について解説しています。デルタ結線(Δ結線)を等価なスター結線(Y結線)に変換するのをデルタスター変換(Δ→Y変換)といいます。デルタスター変換の式の導出方法についても解説していますので参考にしてみてください。
- スターデルタ変換(Y→Δ変換)
- スターデルタ変換(Y→Δ変換)について解説しています。スター結線(Y結線)を等価なデルタ結線(Δ結線)に変換するのをスターデルタ変換(Y→Δ変換)といいます。スターデルタ変換の式の導出方法についても解説していますので参考にしてみてください。
- 交流回路のテブナンの定理
- 交流回路のテブナンの定理(鳳-テブナンの定理)について解説しています。テブナンの定理を使った交流回路の計算方法や、交流回路のテブナンの定理の証明についても解説していますので参考にしてみてください。


