スポンサーリンク
交流回路の位相
※ページ内にPR・広告が含まれる場合があります。
またよく分からない言葉がでてきました。
位相?
直流回路の計算をするときには位相を考える必要はないのですが、交流回路の計算をするときには位相を考えなければならない場合があります。
このページでは、位相、位相差、位相の遅れ進みなどについて解説していますので、位相や位相差とは何か? 位相の遅れ進みとはどういうものか? などについて勉強してみましょう。
スポンサーリンク
位相とは?
位相は、波形の時間的なズレのことをいいます。(「時間的なズレ」とは、下の図でいう横方向(時間軸方向)のズレのことです。)
例えば、次のような電圧波形と電流波形があるとします。
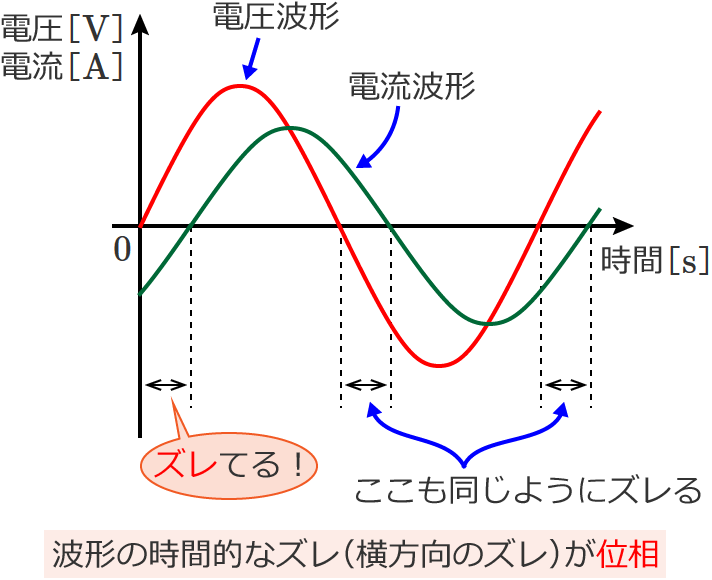
この図の「電圧波形」と「電流波形」を比べると、電流波形が電圧波形よりも右方向にズレてますよね?
このズレは2つの波形の位相に差がある(時間的なズレ方に差がある)ことにより生じるもので、この位相の差(時間的なズレの差)を位相差といいます。
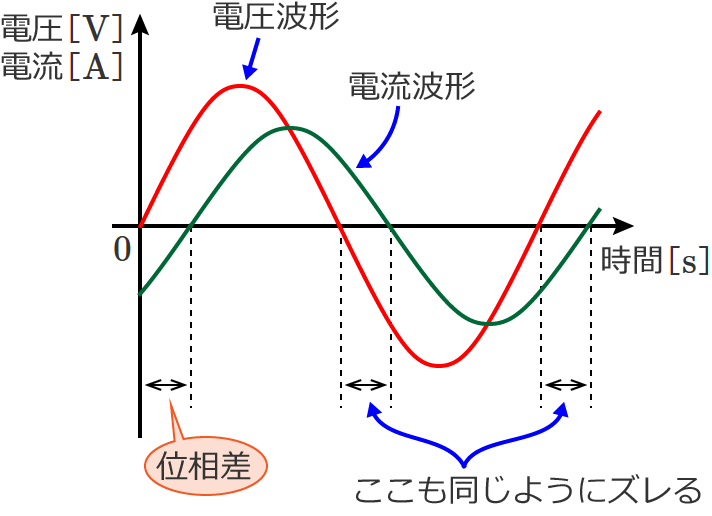
位相差は角度で表わされるので、位相差の単位は角度の単位と同じ「 ${}^\circ$ 」(度)になります。
また、位相には、波形のズレ方によって同位相、遅れ位相、進み位相があります。
次に、これら3つの位相(同位相、遅れ位相、進み位相)について、電圧波形と電流波形を例にして解説します。
同位相
同位相は「同相」ともいい、次のように電圧波形と電流波形にズレがないものをいいます。
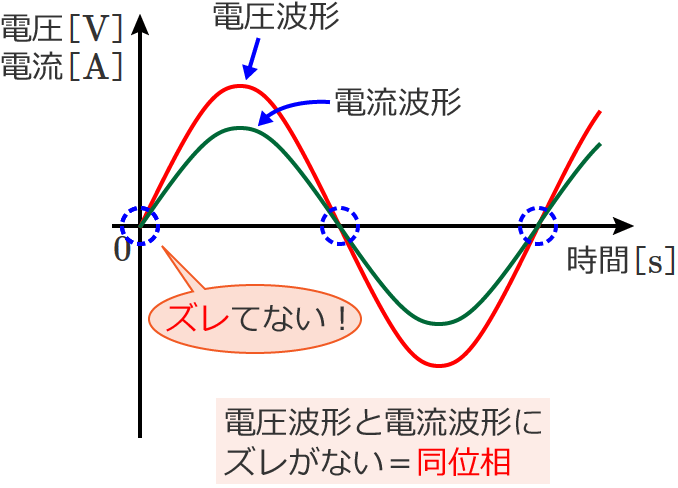
遅れ位相
遅れ位相は、次のように電圧波形に対して電流波形が右にズレているものをいいます。
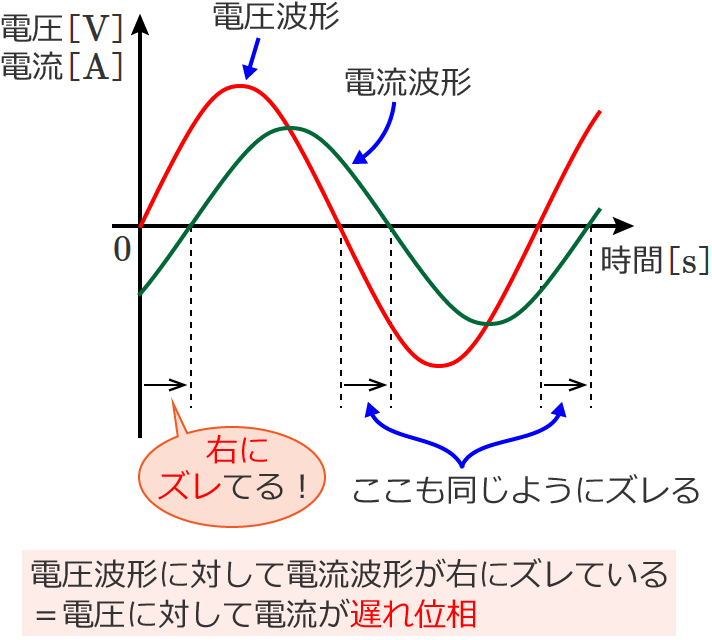
ここで注意してほしいのは、「遅れ位相」、「進み位相」を言う場合は、「○○に対して遅れ位相」とか「○○に対して進み位相」と言うということです。
つまり、位相の基準になるものは何か?を示して、何が遅れか? 進みか? ということです。
したがってこの場合、もし電流を基準にして電圧の位相をいえば、「電流に対して電圧は進み位相」ということになります。
ただ、一般的には「電圧を基準として電流のことを」いうことが多いので、「遅れ位相」といえば、ふつうは上の図のように「電圧に対して電流が右側にズレている波形」のことをいいます。
基準が何かを意識しないと、遅れ位相と進み位相がゴチャゴチャになるので注意してください。
進み位相
進み位相は、次のように電圧波形に対して電流波形が左にズレているものをいいます。
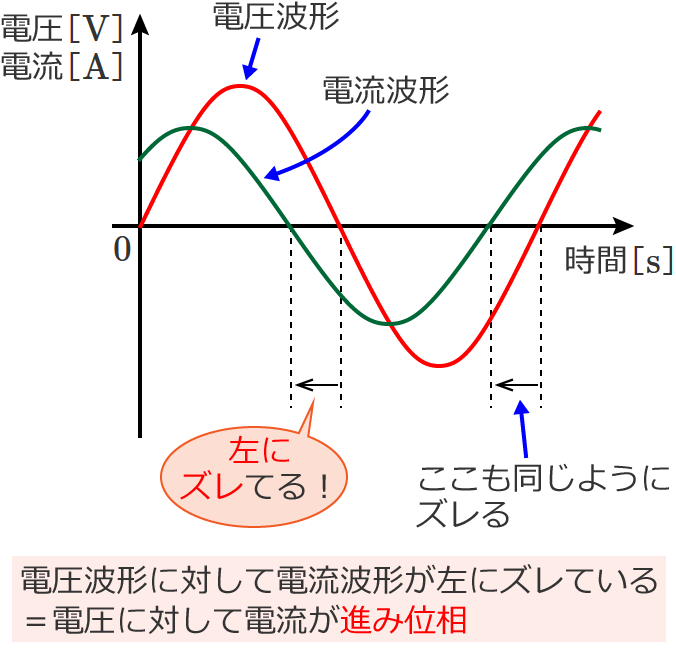
これも遅れ位相で説明したように、電流を基準にして電圧の位相をいえば、「電流に対して電圧は遅れ位相」ということになります。
以上が同位相、遅れ位相、進み位相の説明になりますが、位相は「ズレ」で、電流波形が右にズレていれば遅れ位相、電流波形が左にズレていれば進み位相とおぼえておけばいいでしょう。(ただし、位相の基準は気にしましょう。)
スポンサーリンク
スポンサーリンク
抵抗にかかる電圧と流れる電流の位相
次のように、交流電源に抵抗が接続された回路があるとします。
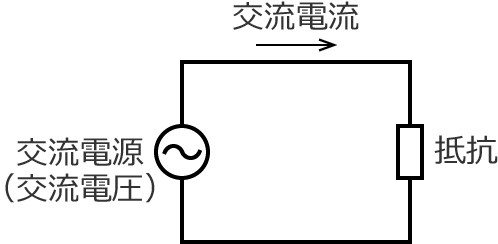
このとき、抵抗にかかる電圧の波形と抵抗に流れる電流の波形は次のようになり、電圧の波形と電流の波形にはズレがありません。
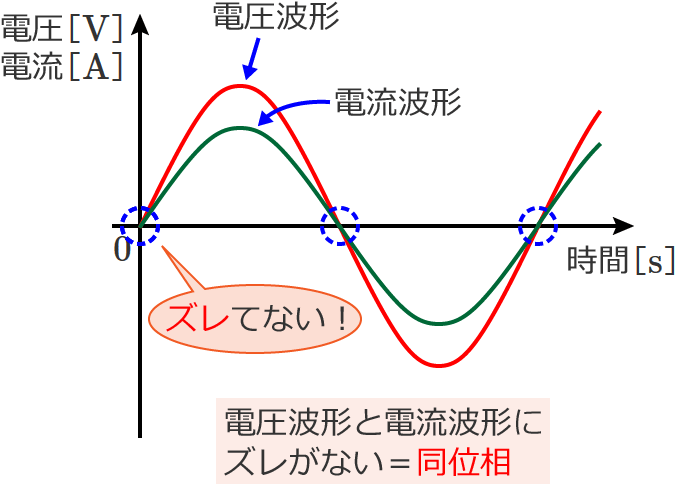
なので、抵抗の場合は、「電圧」と「電流」が同位相になります。(つまりこの場合、位相差は $0^\circ$ )
抵抗だけの回路の場合、同位相(電圧波形と電流波形にズレがない)になるので、基本的には直流回路と考え方は同じ(位相を考えなくて良い)になります。
コイルにかかる電圧と流れる電流の位相
ここまでは抵抗の話ばかりでしたが、電気回路、特に交流回路ではコイルというものとコンデンサというものがよく扱われます。
コイルって何?
コイルとは、簡単にいうと、電線をぐるぐる巻いたようなものです。
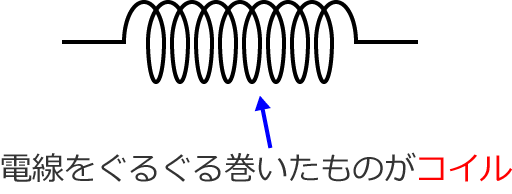
ちなみに、このコイルの中に鉄心(鉄の棒)を入れて、電池をつなぐと電磁石になります。小学校か中学校の理科の授業で実験したような…。
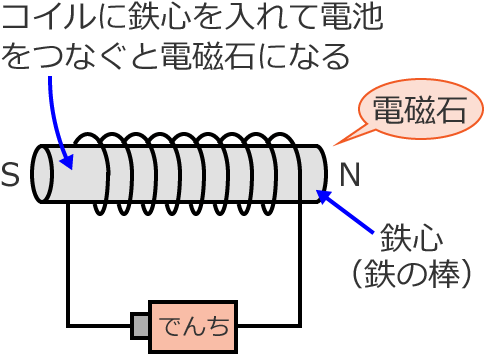
コイルとはこのようなものですが、このコイルに交流電源が接続された次のような回路があるとします。
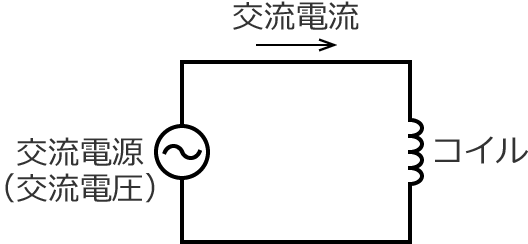
このとき、コイルにかかる電圧の波形とコイルに流れる電流の波形は次のようになり、電圧の波形に対して電流の波形は右に $90^\circ$ ズレます。
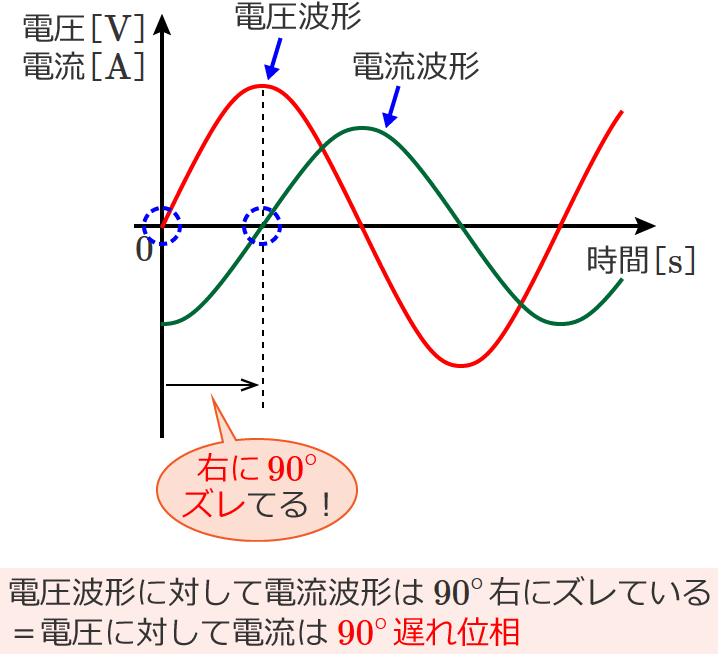
なので、コイルの場合は、「電圧」に対して「電流」が $\boldsymbol{90^\circ}$ 遅れ位相になります。
なぜ、コイルの場合の位相の大きさは90°になるのか?
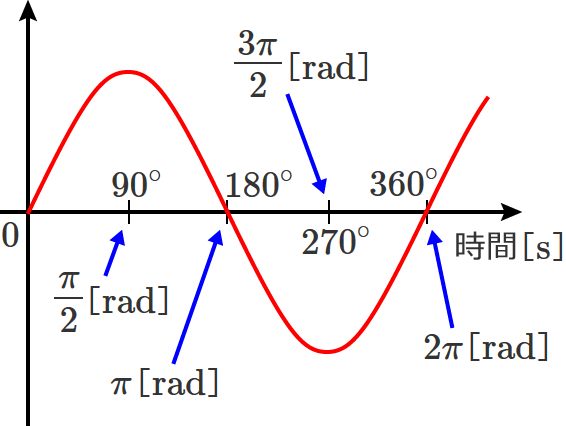
波 $1$ 個分の長さを角度で表わすと $360^\circ$ になります。(次の図は電圧波形について書いていますが、電流波形の場合でも波 $1$ 個分で $360^\circ$ になります。)
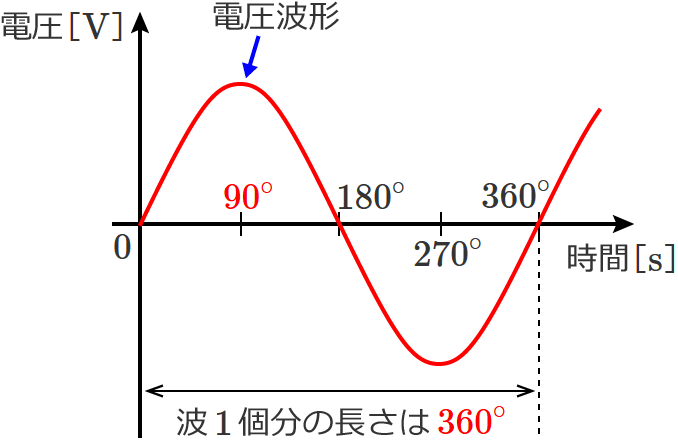
コイルの場合は、電圧波形に対して電流波形が波 $1$ 個分の $\dfrac{1}{4}$ 右にズレるので、$\dfrac{360^\circ}{4} =90^\circ$ 右にズレることになります。
ちょっと難しい計算(微分を使う)をすると $90^\circ$ ズレることを説明できるのですが、第二種電気工事士の学科試験では微分・積分は範囲外なので、ここでは説明しません。(コイルの場合に $90^\circ$ ズレる理由を知りたい方はなぜコイルに流れる電流の位相は電圧より90°遅れるのか?のページを参考にしてみてください。)
位相の単位
位相(角度)の単位には「 ${}^\circ$ 」(度)の他に「 $\mathrm{rad}$ 」(ラジアンと読む)もあります。
第二種電気工事士学科試験では「ラジアン」による出題はほとんどないのでここでは解説しませんが、位相の単位にはラジアンという単位もあることはおぼえておくといいと思います。
ちなみに、$360$[$\mathrm{°}$]=$2\pi$[$\mathrm{rad}$]になります。( $\pi$ って、円周率($=3.14\ldots$)のパイです。)
コンデンサにかかる電圧と流れる電流の位相
次は、コンデンサの場合です。
抵抗、コイルの他にコンデンサも交流回路でよく扱われます。
コンデンサって何?
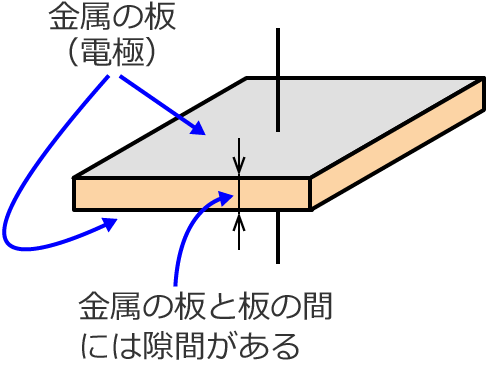
コンデンサとは、簡単にいうと、金属の板を2枚向かい合わせたようなものです。この金属の板は「電極」と呼ばれます。
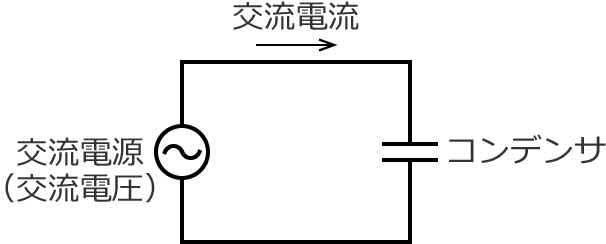
コンデンサはこのようなものですが、このコンデンサに交流電源が接続された次のような回路があるとします。
このとき、コンデンサにかかる電圧の波形とコンデンサに流れる電流の波形は次のようになり、電圧の波形に対して電流の波形は左に $90^\circ$ ズレます。
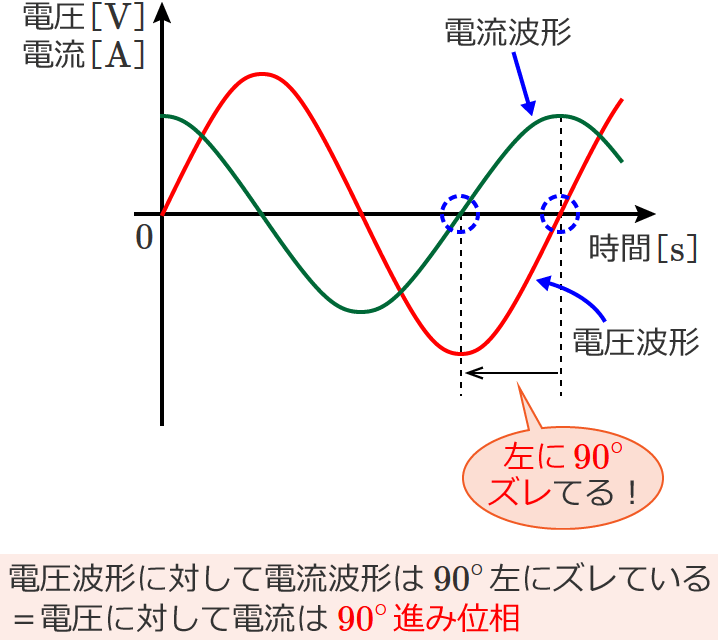
なので、コンデンサの場合は、「電圧」に対して「電流」が $\boldsymbol{90^\circ}$ 進み位相になります。
スポンサーリンク
スポンサーリンク
コンデンサの場合に $90^\circ$ ズレる理由を知りたい方はなぜコンデンサに流れる電流の位相は電圧より90°進むのか?のページを参考にしてみてください。ただし、このページでの計算については第二種電気工事士学科試験では出題されないので、ふ〜んって読んでみる程度でいいと思います。
正弦波交流波形 ←BACK
NEXT→ 交流回路のリアクタンス
スポンサーリンク
交流回路の位相 関連ページ
- 電圧・電流・抵抗
- 第二種電気工事士学科試験の「電気理論」の問題を解くためにおぼえておかなければならない「電圧・電流・抵抗」についてまとめています。「電圧・電流・抵抗」は電気の計算をするために一番初めに理解しておかなくてはならないとても重要な項目なので、しっかりと勉強しておきましょう。
- オームの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「オームの法則」についてまとめています。「オームの法則」は電気の計算をするときの一番基本的な法則になりますので、しっかり勉強しておきましょう。
- 電線の抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「電線の抵抗」についてまとめています。「電線の抵抗」は第二種電気工事士の学科試験でよく出題される重要な項目ですので、しっかり勉強しておきましょう。
- 直列接続と並列接続
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「直列接続と並列接続」についてまとめています。「直列接続と並列接続」は電気回路の基本になる接続方法です。
- 合成抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「合成抵抗」についてまとめています。第二種電気工事士の学科試験では、「合成抵抗」を求める問題がよく出題されています。
- キルヒホッフの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「キルヒホッフの法則」についてまとめています。「キルヒホッフの法則」は電気の計算をするときの重要な法則になりますので、しっかり勉強しておきましょう。
- 直流回路と交流回路
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路と交流回路」についてまとめています。交流回路の最大値と実効値の関係はとても重要で、学科試験でもたまに出題されています。
- 直流回路の計算(基本)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路の計算(基本)」についてまとめています。まずは簡単な直流回路の計算をできるようになりましょう。
- 直流回路の計算(分圧と分流)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「分圧」と「分流」についてまとめています。「分圧」と「分流」は電気回路の計算をするときの考え方の基本になります。
- 電力・電力量・発熱量
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「電力・電力量・発熱量」についてまとめています。電力、電力量、発熱量の違いとそれぞれの求め方をおぼえましょう。
- 正弦波交流波形
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときにおぼえておかなければならない「正弦波交流波形」についてまとめています。「正弦波交流」の最大値または実効値を求める問題は試験でも度々出題されていますので、最大値と実効値の関係式は必ずおぼえておきましょう。
- 交流回路のリアクタンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のリアクタンス」についてまとめています。コイルのリアクタンス(誘導性リアクタンス)とコンデンサのリアクタンス(容量性リアクタンス)の違いをおぼえておきましょう。
- 交流回路のインピーダンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のインピーダンス」についてまとめています。インピーダンスというとちょっとむずかしそうですが、おぼえると簡単です。
- 電気でよく使われる単位
- 第二種電気工事士学科試験の「電気理論」分野で出題される「電気でよく使われる単位」についてまとめています。「単位」は電気を勉強するときの基本中の基本になりますので、しっかりおぼえておきましょう。
- 電気でよく使われるギリシャ文字
- 第二種電気工事士学科試験の計算問題などや単位などで使用されるギリシャ文字の読み方と表わす意味についてまとめています。電気の世界に限らず理系の分野では、色々な量を表わしたり、単位の補助記号としてギリシャ文字が使用されますが、代表的なものだけでもおぼえておくようにしましょう。


