スポンサーリンク
電気のお勉強 交流回路
※ページ内にPR･広告が含まれる場合があります。
「交流回路」の関連記事のまとめページです。
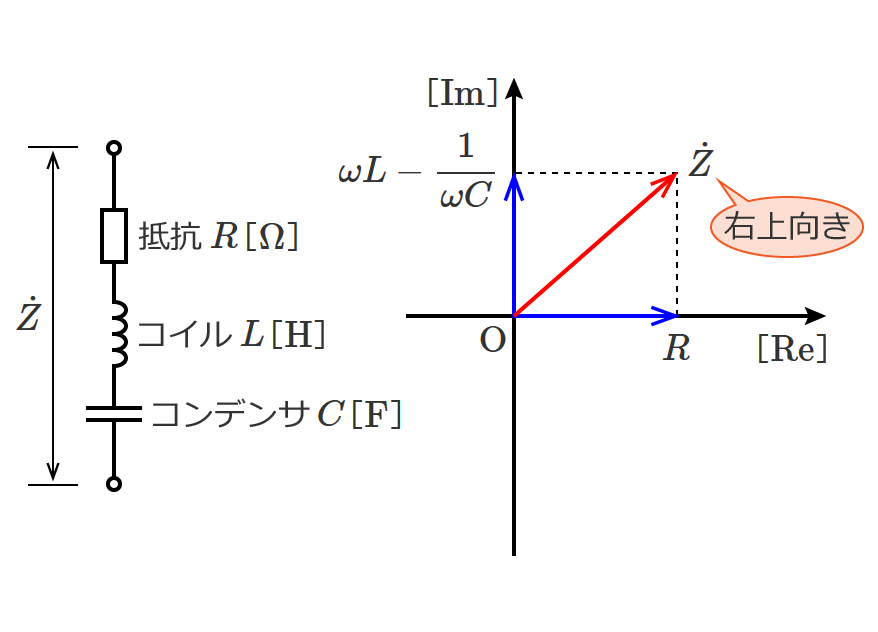
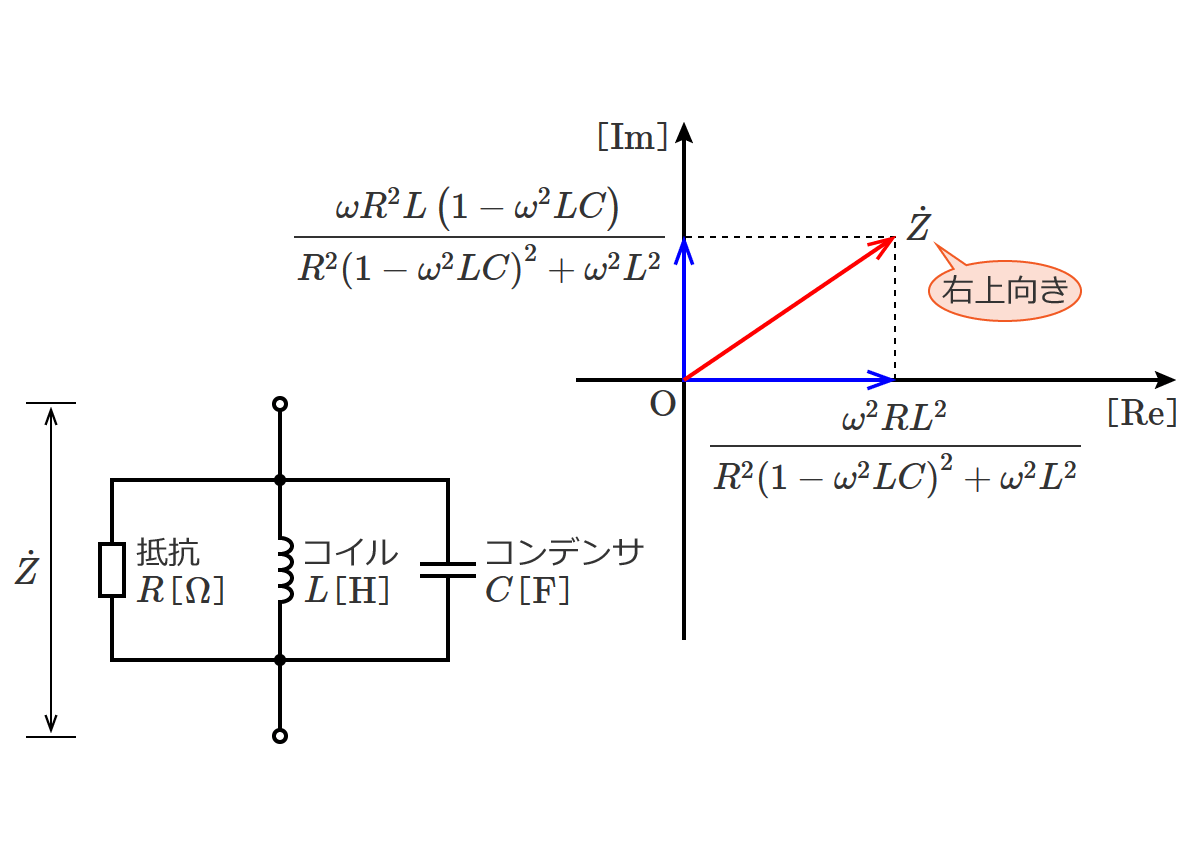
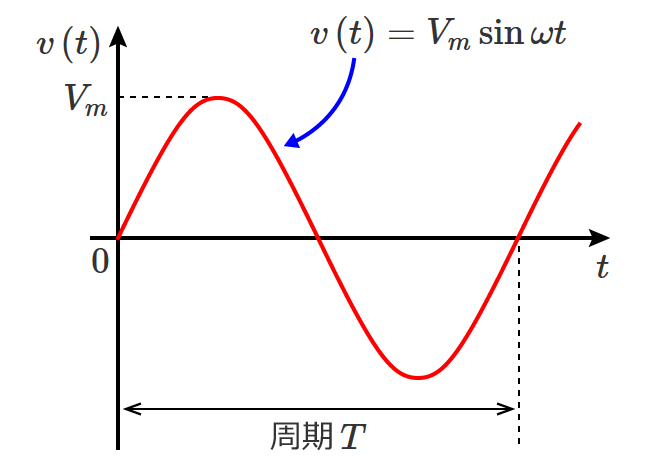
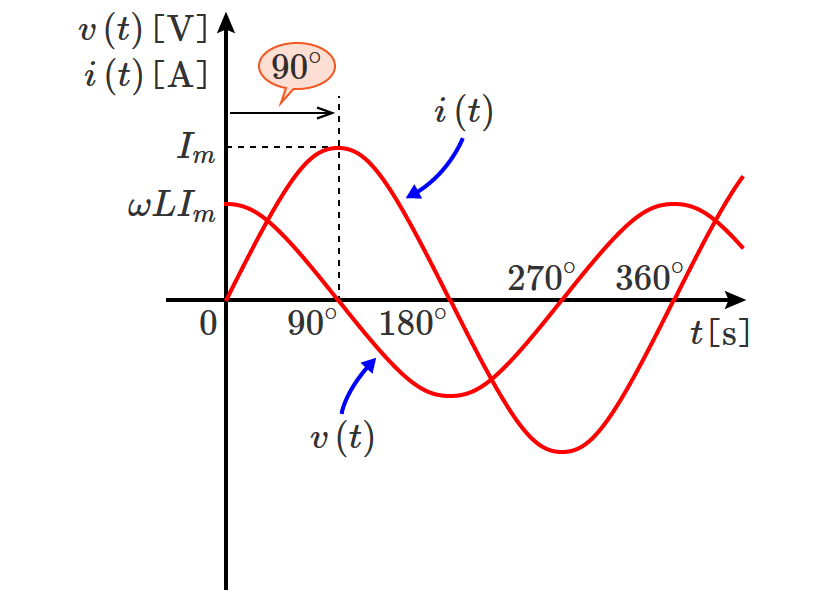
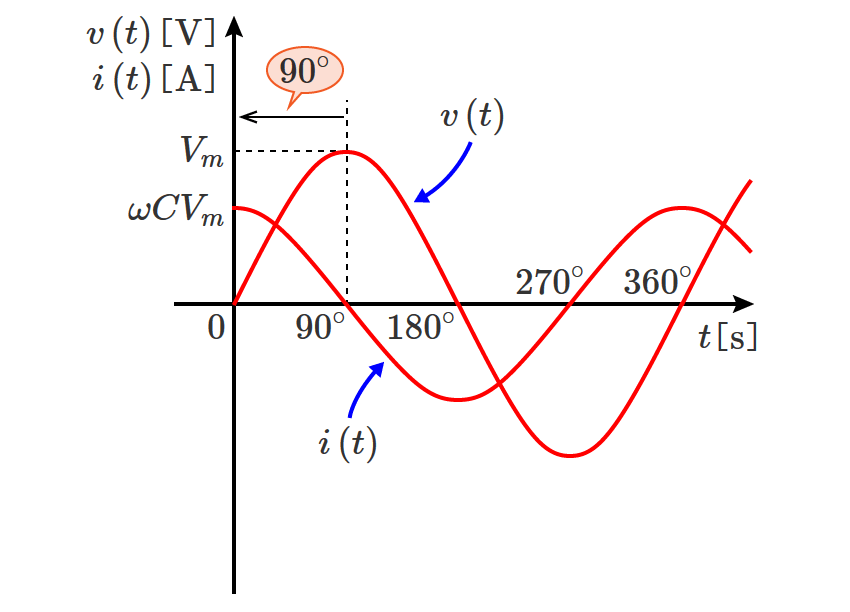
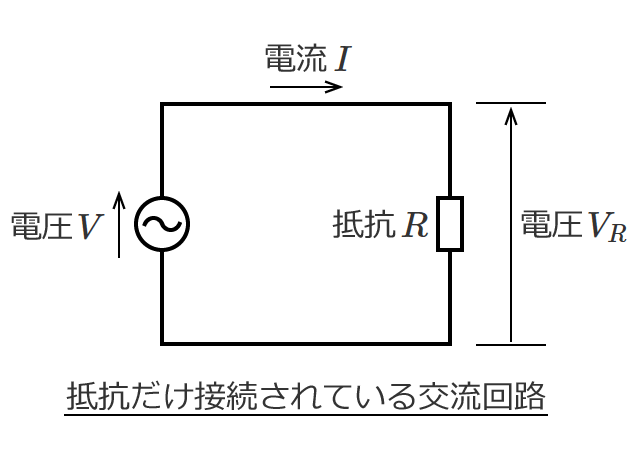
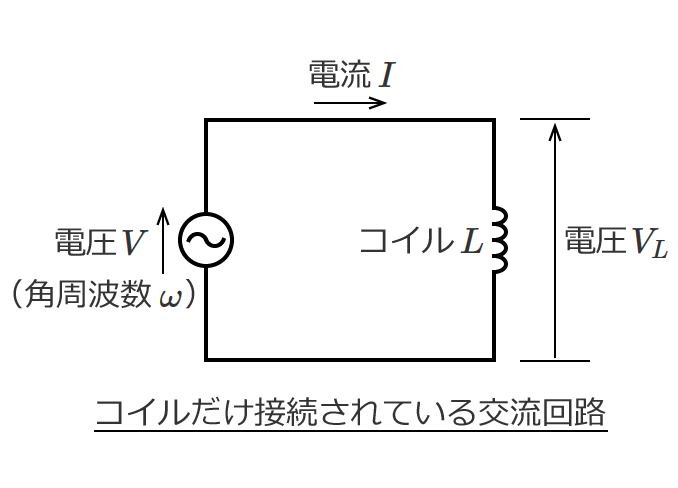
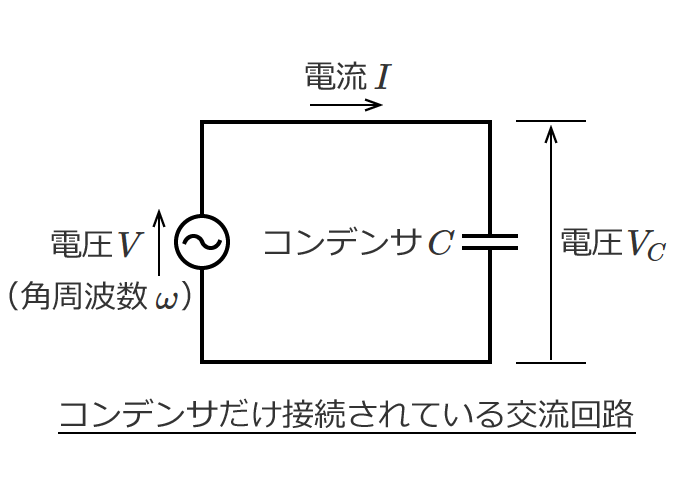
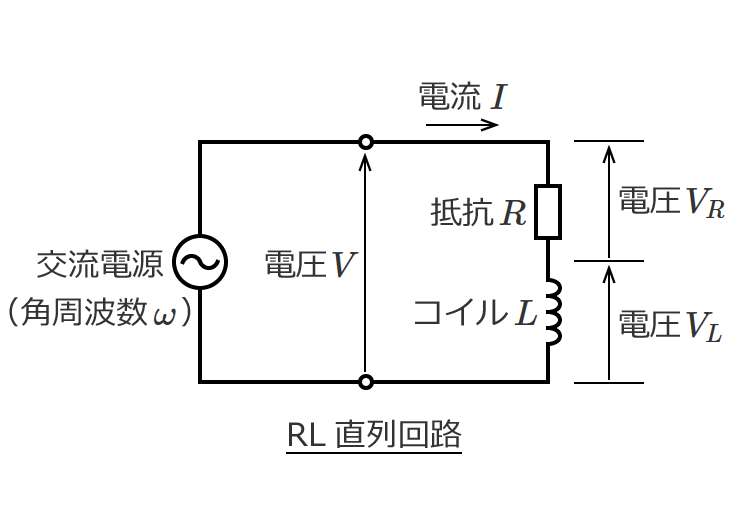
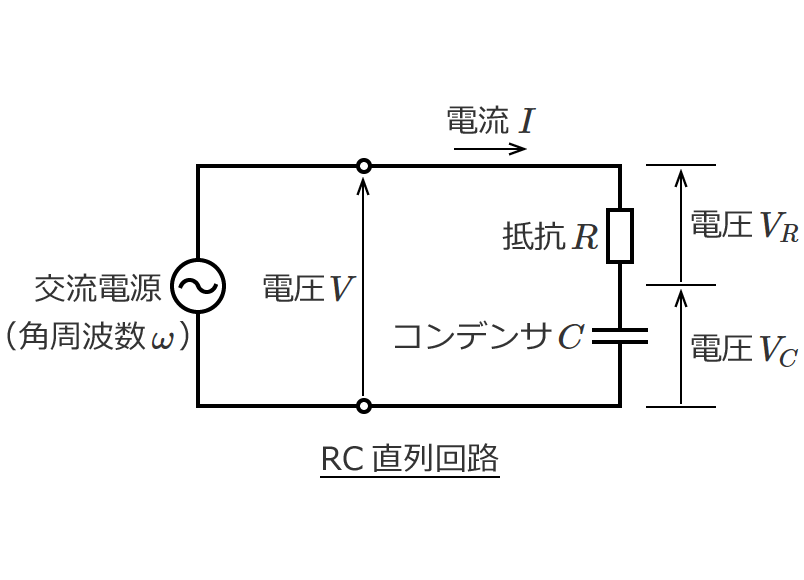
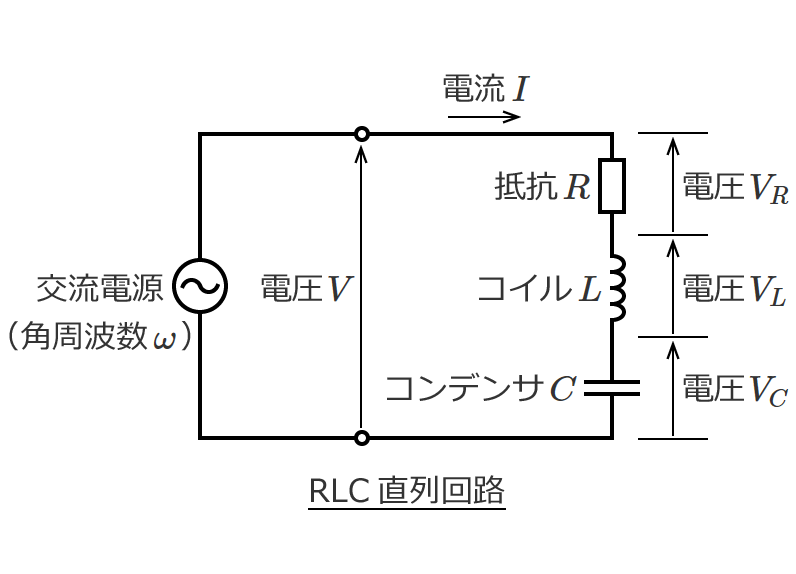
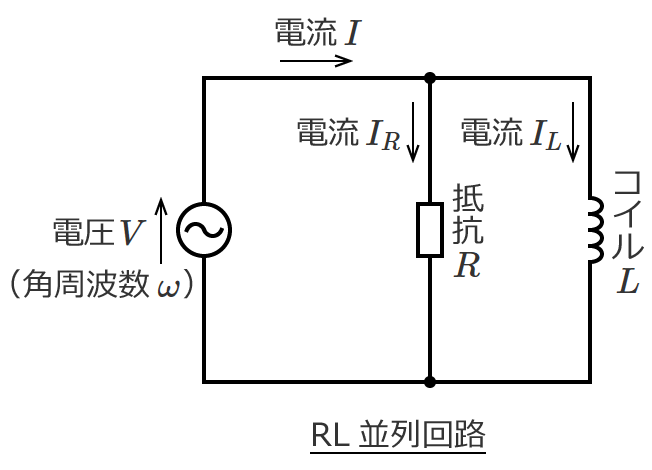
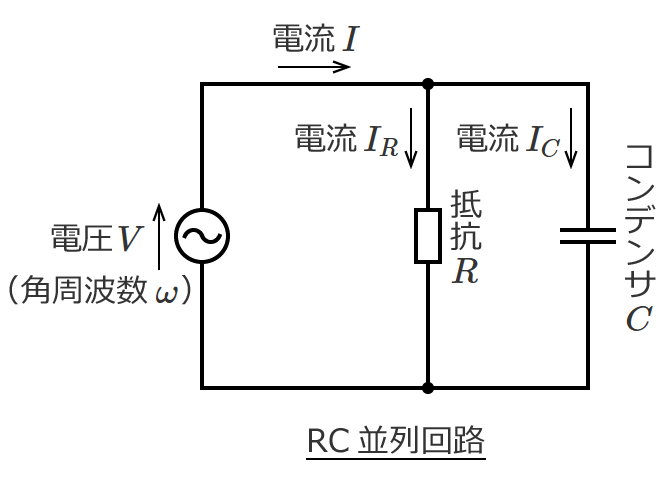
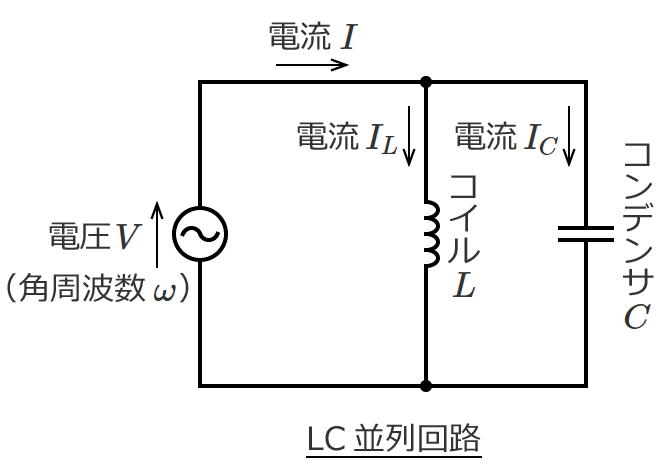
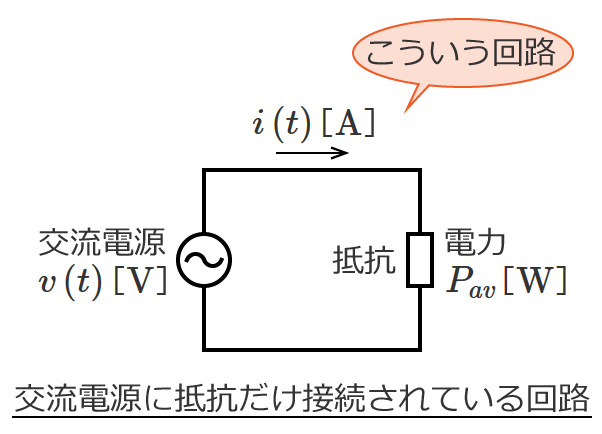
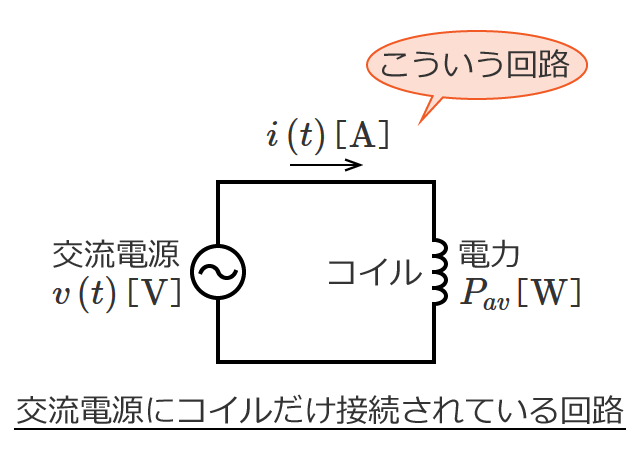
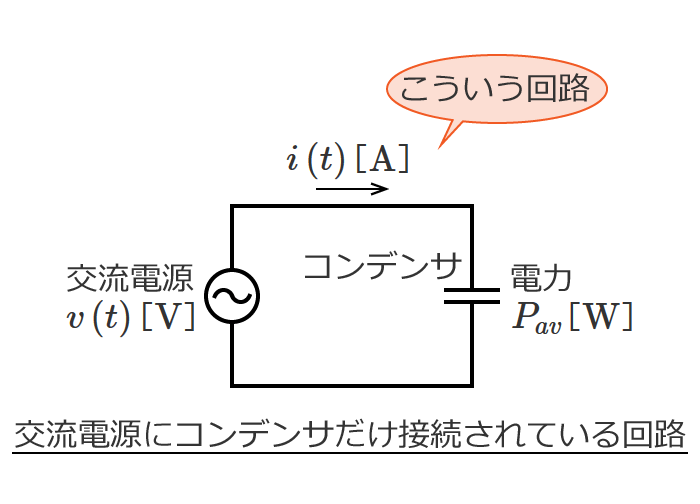
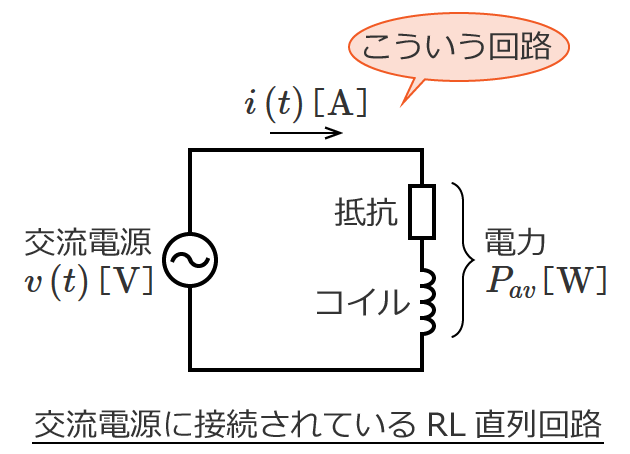
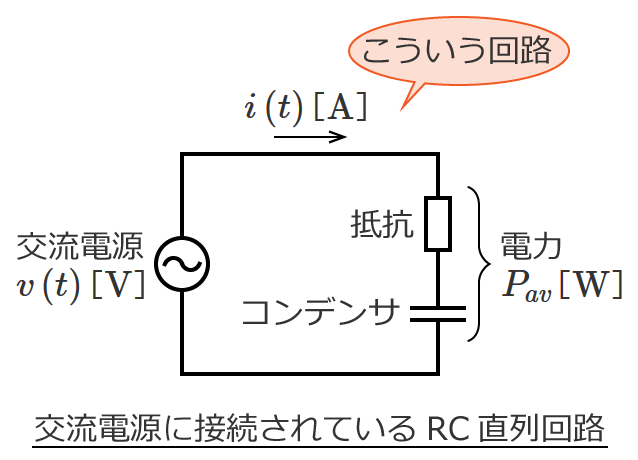
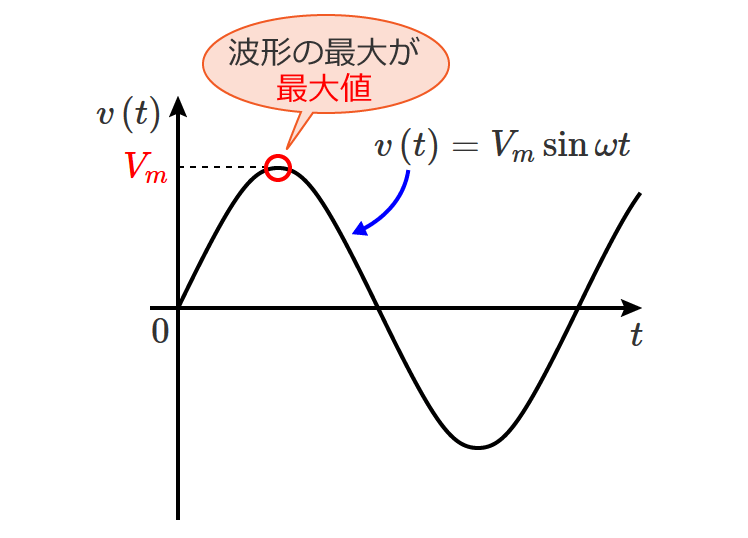
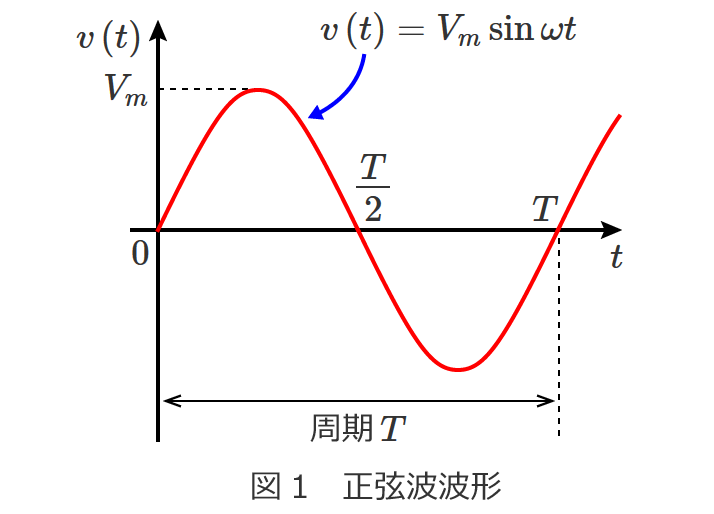
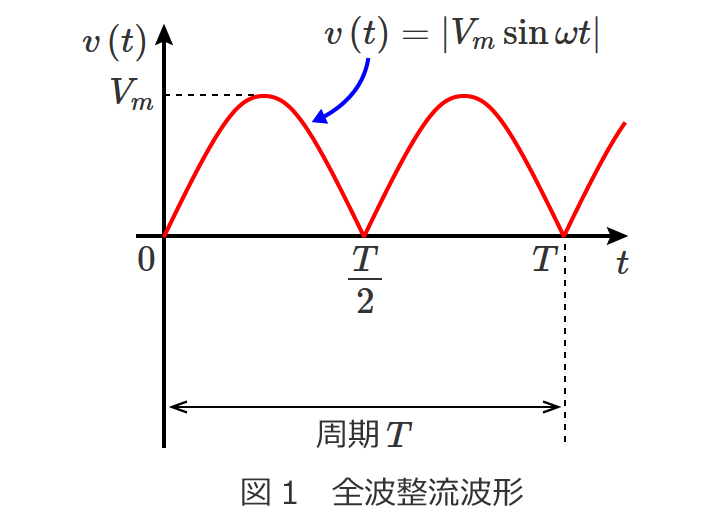
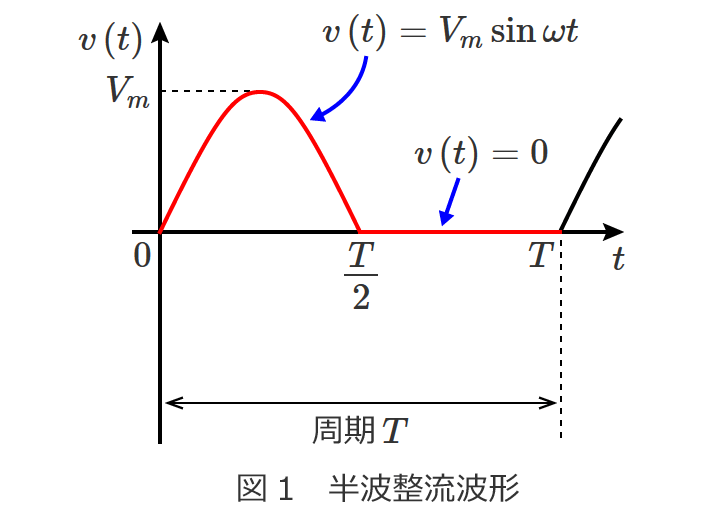
直流回路の場合、回路素子として抵抗だけを考えればいい問題がほとんどですが、交流回路の問題になると回路素子としてコイルとコンデンサが含まれてきます。
交流回路の計算では、
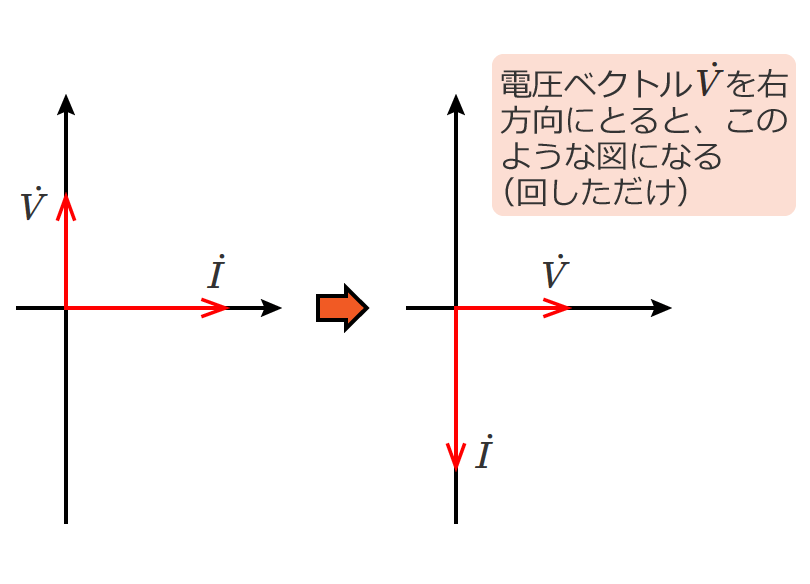
- 位相
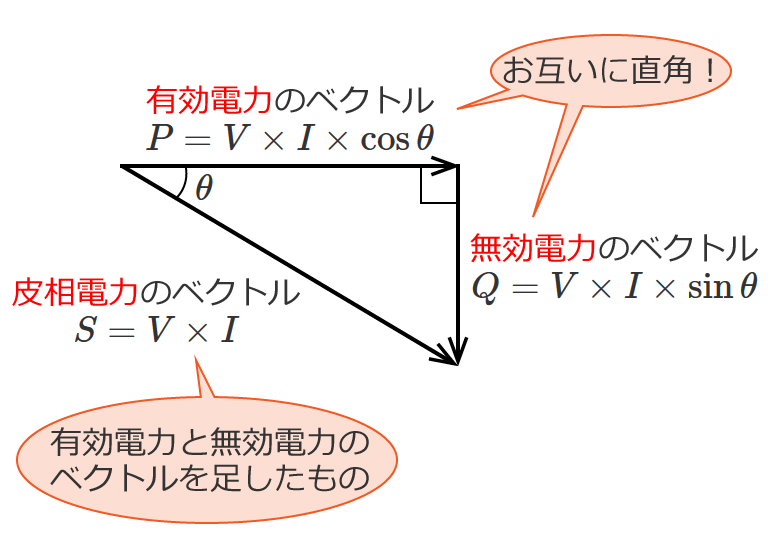
- 力率
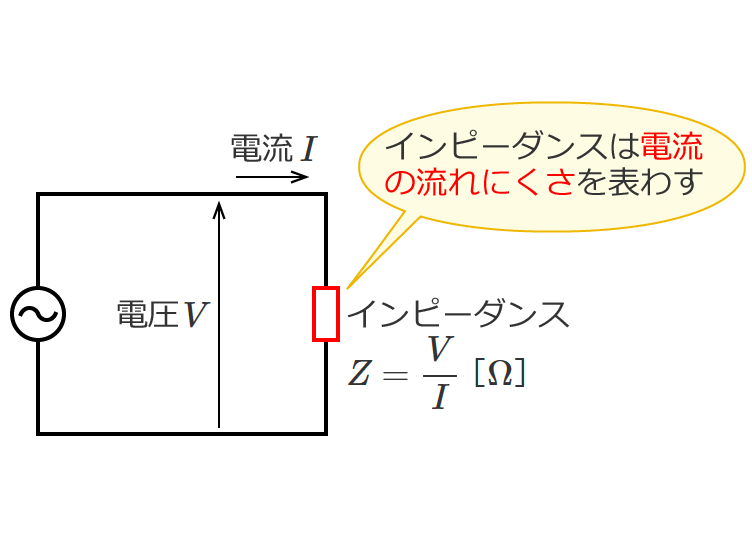
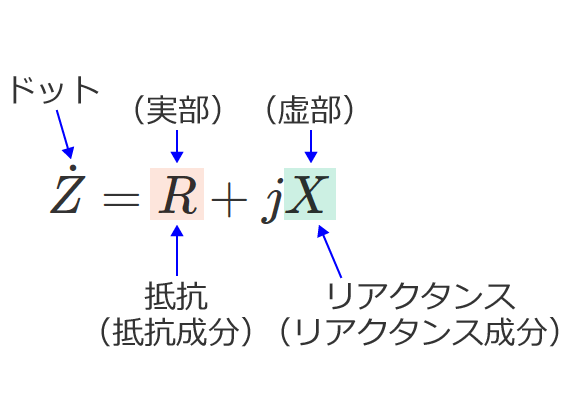
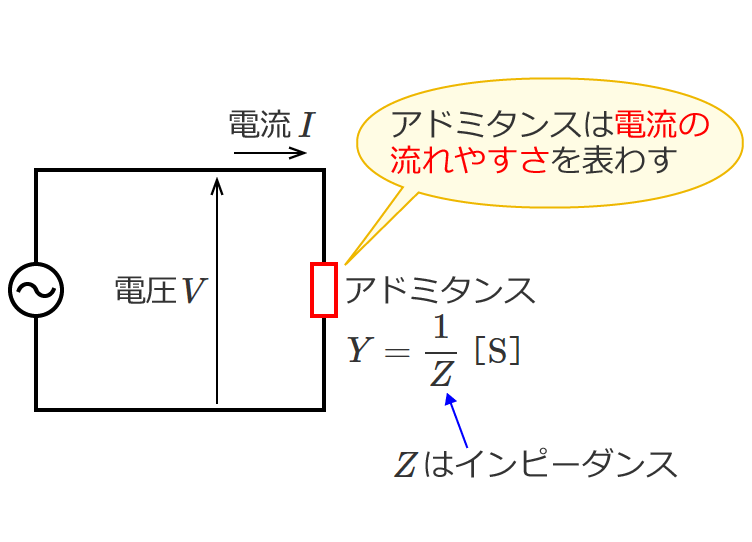
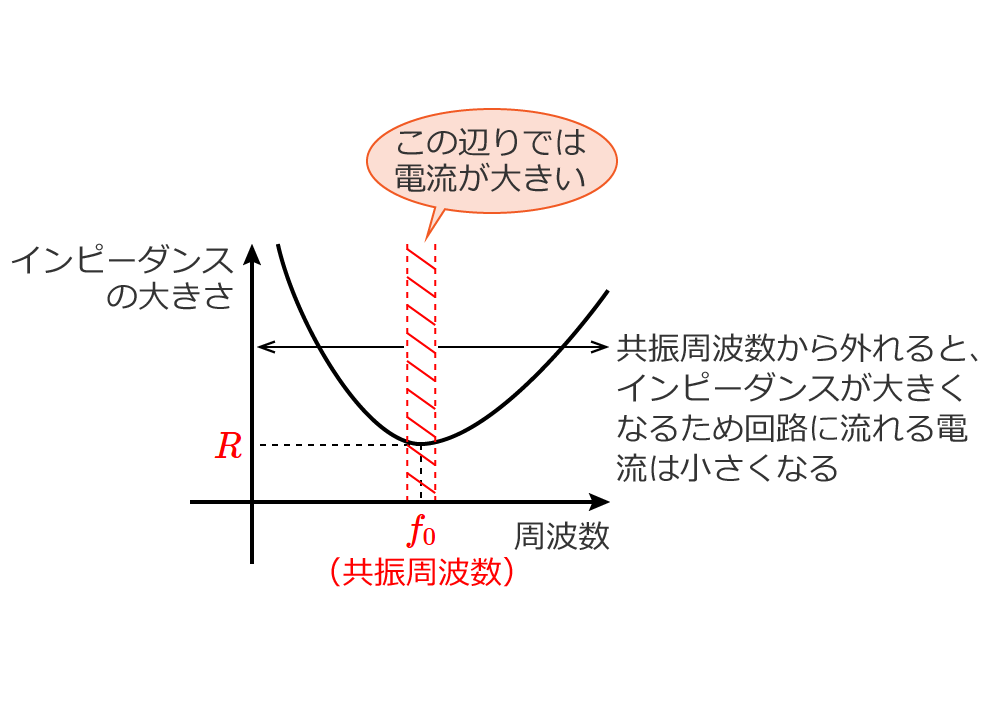
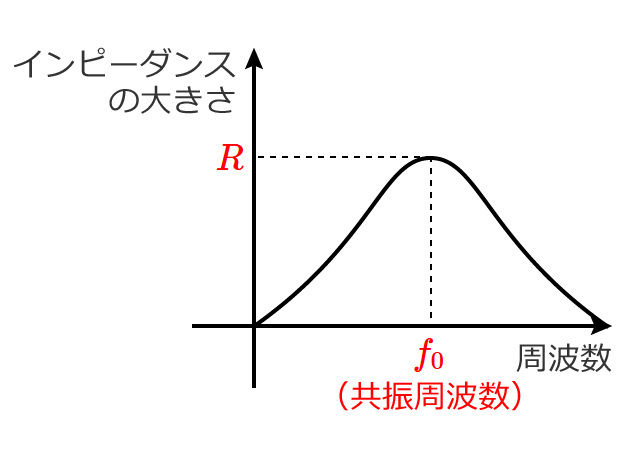
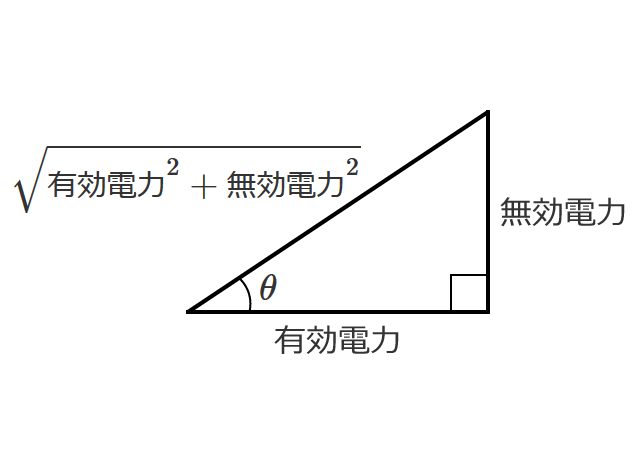
- インピーダンス
など直流回路では扱わないものがありますが、回路の計算の基本となる電圧や電流を求める計算方法は直流回路の計算方法がベースになります。
スポンサーリンク
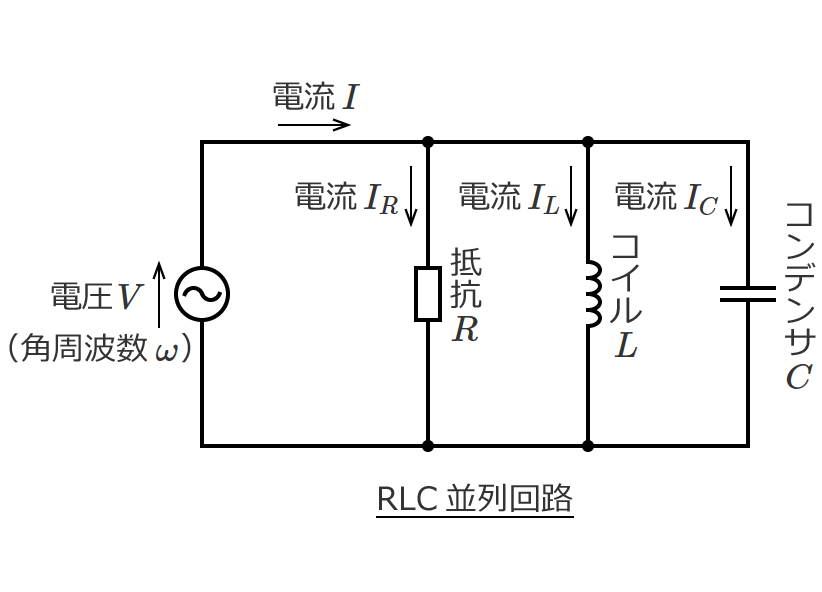
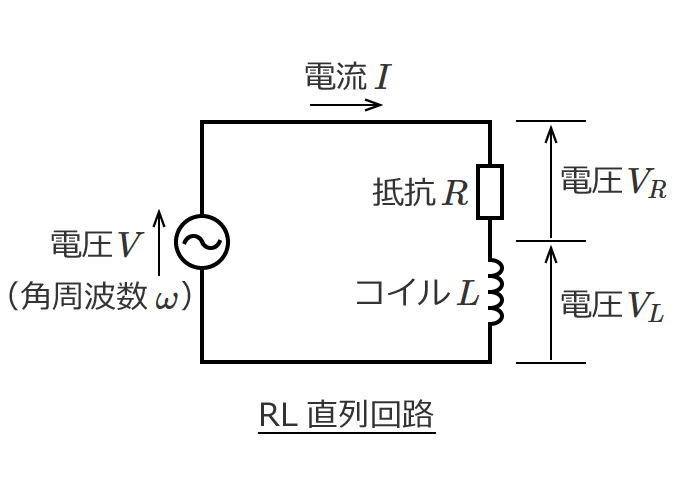
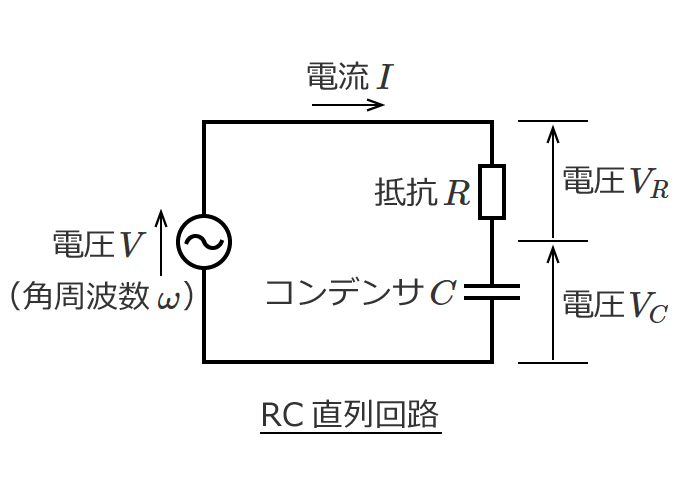
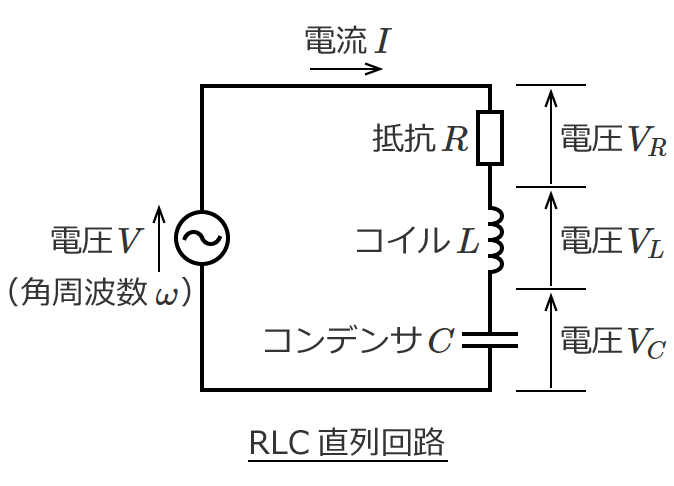
電気のお勉強 交流回路 関連記事一覧
交流回路での電圧と電流の比をインピーダンスといい、インピーダンスの大きさは、交流回路の電流の流れにくさを表わします。インピーダンスを表わす量記号には「 $Z$ 」が使われ、インピーダンスの単位は直流回路の抵抗と同じ「 $\Omega$ 」（オーム）になります。インピーダンスの大きさは電流の流れにくさ...
次のように複素数で表わされたインピーダンスを複素インピーダンスといい、複素インピーダンスの単位は抵抗と同じ「 $\Omega$ 」（オーム）になります。$\dot{Z} =R+jX$ ［$\Omega$］ …① （複素インピーダンス）複素インピーダンスは、単にインピーダンスとも呼ばれます...
インピーダンスの逆数をアドミタンスといい、アドミタンスの大きさは、交流回路の電流の流れやすさを表わします。アドミタンスを表わす量記号には「 $Y$ 」が使われ、アドミタンスの単位はコンダクタンスと同じ「 $\mathrm{S}$ 」（ジーメンスと読む）になります。抵抗の逆数をコンダクタンスといいます...
次のように複素数で表わされたアドミタンスを複素アドミタンスといい、複素アドミタンスは複素インピーダンスの逆数になります。複素アドミタンスの単位はコンダクタンスと同じ「 $\mathrm{S}$ 」（ジーメンスと読む）になります。$\dot{Y} =G+jB$ ［$\mathrm{S}$］ …]...
回路の素子（抵抗 $R$ 、コイル $L$ 、コンデンサ $C$ ）が1個の場合のインピーダンスを計算してみます。素子（ $R$ 、$L$ 、$C$ ）が1個の場合なので計算というほどの計算でもありませんが、インピーダンスを求める計算の基礎の基礎なのでとりあえず…。（ここでつまずいちゃダメですよ。）...
回路の素子（抵抗 $R$ 、コイル $L$ 、コンデンサ $C$ ）が2個直列接続されている場合の合成インピーダンスを計算してみます。抵抗RとコイルLの直列回路の合成インピーダンス（RL直列回路）RL直列回路の合成インピーダンスRL直列回路は、抵抗 $R$ とコイル $L$ が直列に接続された回路で...
回路の素子（抵抗 $R$ 、コイル $L$ 、コンデンサ $C$ ）が2個並列接続されている場合の合成インピーダンスを計算してみます。抵抗RとコイルLの並列回路の合成インピーダンス（RL並列回路）RL並列回路の合成インピーダンスRL並列回路は、抵抗 $R$ とコイル $L$ が並列に接続された回路で...
回路の素子が3個（抵抗 $R$ 、コイル $L$ 、コンデンサ $C$ ）直列接続されたRLC直列回路の合成インピーダンスを計算してみます。抵抗RとコイルLとコンデンサCの直列回路の合成インピーダンス（RLC直列回路）RLC直列回路の合成インピーダンスRLC直列回路は、抵抗 $R$ とコイル $L$...
回路の素子が3個（抵抗 $R$ 、コイル $L$ 、コンデンサ $C$ ）並列接続されたRLC並列回路の合成インピーダンスを計算してみます。抵抗RとコイルLとコンデンサCの並列回路の合成インピーダンス（RLC並列回路）RLC並列回路の合成インピーダンスRLC並列回路は、抵抗 $R$ とコイル $L$...
RLC直列共振回路って何？交流回路でRLC直列共振回路というのがあります。このRLC直列共振回路とはどんな回路なのでしょうか？RLC直列共振回路の回路図を書いてみると、次のような回路になります。あれ？ 抵抗 $R$ 、コイル $L$ 、コンデンサ $C$ を直列にただ接続しただけのRLC直列回路と同...
RLC並列共振回路って何？交流回路でRLC並列共振回路というのがあります。このRLC並列共振回路とはどんな回路なのでしょうか？RLC並列共振回路の回路図を書いてみると、次のような回路になります。あれ？ 抵抗 $R$ 、コイル $L$ 、コンデンサ $C$ を並列にただ接続しただけのRLC並列回路と同...
正弦波交流波形の実効値と最大値の関係はよく知られているように、実効値＝最大値÷$\sqrt{2}$という関係になります。これはみなさんもよく知っていることかと思いますが、では、なぜ、最大値を $\sqrt{2}$ で割れば実効値になるのでしょうか？これは、次の実効値の定義式を使って、正弦波交流波形の...
コイルに正弦波交流電圧をかけると、電流の位相は電圧に対して90°遅れ位相になります。コイルの場合、なぜ電流が90°遅れ位相になるのか計算から導出してみます。次の図のように、正弦波交流電圧 $v \left( t \right)$ にコイル $L$ が接続された回路を考えます。このとき、回路に流れる電...
コンデンサに正弦波交流電圧をかけると、電流の位相は電圧に対して90°進み位相になります。コンデンサの場合、なぜ電流が90°進み位相になるのか計算から導出してみます。次の図のように、正弦波交流電圧 $v \left( t \right)$ にコンデンサ $C$ が接続された回路を考えます。このとき、回...
電圧 $\dot{V}$［$\mathrm{V}$］の正弦波交流電源に、$R$［$\Omega$］の抵抗が接続されている次のような交流回路があるとします。この交流回路において、正弦波交流電源の電圧を $\dot{V} =V$（ $\dot{V} =V+j\, 0$ ）［$\mathrm{V}$］とし...
電圧 $\dot{V}$［$\mathrm{V}$］の正弦波交流電源に、インダクタンス $L$［$\mathrm{H}$］のコイルが接続されている次のような交流回路があるとします。この交流回路において、正弦波交流電源の電圧を $\dot{V} =V$（ $\dot{V} =V+j\, 0$ ）［$\...
電圧 $\dot{V}$［$\mathrm{V}$］の正弦波交流電源に、静電容量 $C$［$\mathrm{F}$］のコンデンサが接続されている次のような交流回路があるとします。この交流回路において、正弦波交流電源の電圧を $\dot{V} =V$（ $\dot{V} =V+j\, 0$ ）［$\m...
正弦波交流電源に、$R$［$\Omega$］の抵抗とインダクタンス $L$［$\mathrm{H}$］のコイルが直列に接続されている次のようなRL直列回路があるとします。図のように、抵抗（ $R$ ）とコイル（ $L$ ）が直列に接続されている回路をRL直列回路といいます。このRL直列回路において、...
正弦波交流電源に、$R$［$\Omega$］の抵抗と静電容量 $C$［$\mathrm{F}$］のコンデンサが直列に接続されている次のようなRC直列回路があるとします。図のように、抵抗（ $R$ ）とコンデンサ（ $C$ ）が直列に接続されている回路をRC直列回路といいます。このRC直列回路において...
正弦波交流電源に、$R$［$\Omega$］の抵抗、インダクタンス $L$［$\mathrm{H}$］のコイル、静電容量 $C$［$\mathrm{F}$］のコンデンサが直列に接続されている次のようなRLC直列回路があるとします。図のように、抵抗（ $R$ ）、コイル（ $L$ ）、コンデンサ（ $...
電圧 $\dot{V}$［$\mathrm{V}$］の正弦波交流電源に、$R$［$\Omega$］の抵抗とインダクタンス $L$［$\mathrm{H}$］のコイルが並列に接続されている次のようなRL並列回路があるとします。図のように、抵抗（ $R$ ）とコイル（ $L$ ）が並列に接続されている回...
電圧 $\dot{V}$［$\mathrm{V}$］の正弦波交流電源に、$R$［$\Omega$］の抵抗と静電容量 $C$［$\mathrm{F}$］のコンデンサが並列に接続されている次のようなRC並列回路があるとします。図のように、抵抗（ $R$ ）とコンデンサ（ $C$ ）が並列に接続されている...
電圧 $\dot{V}$［$\mathrm{V}$］の正弦波交流電源に、インダクタンス $L$［$\mathrm{H}$］のコイルと静電容量 $C$［$\mathrm{F}$］のコンデンサが並列に接続されている次のようなLC並列回路があるとします。図のように、コイル（ $L$ ）とコンデンサ（ $C...
電圧 $\dot{V}$［$\mathrm{V}$］の正弦波交流電源に、$R$［$\Omega$］の抵抗、インダクタンス $L$［$\mathrm{H}$］のコイル、静電容量 $C$［$\mathrm{F}$］のコンデンサが並列に接続されている次のようなRLC並列回路があるとします。図のように、抵抗...
電圧 $\dot{V}$［$\mathrm{V}$］の正弦波交流電源に、$R$［$\Omega$］の抵抗とインダクタンス $L$［$\mathrm{H}$］のコイルが直列に接続されている次のようなRL直列回路があるとします。図のように、抵抗（ $R$ ）とコイル（ $L$ ）が直列に接続されている回...
電圧 $\dot{V}$［$\mathrm{V}$］の正弦波交流電源に、$R$［$\Omega$］の抵抗と静電容量 $C$［$\mathrm{F}$］のコンデンサが直列に接続されている次のようなRC直列回路があるとします。図のように、抵抗（ $R$ ）とコンデンサ（ $C$ ）が直列に接続されている...
電圧 $\dot{V}$［$\mathrm{V}$］の正弦波交流電源に、$R$［$\Omega$］の抵抗、インダクタンス $L$［$\mathrm{H}$］のコイル、静電容量 $C$［$\mathrm{F}$］のコンデンサが直列に接続されている次のようなRLC直列回路があるとします。図のように、抵抗...
正弦波交流電源に抵抗だけ接続されている次のような回路において、この回路の電力（平均電力）$P_{av}$ を、電圧の瞬時値 $v\left( t\right)$ と電流の瞬時値 $i\left( t\right)$ から求めてみます。電力（平均電力）$P_{av}$ を求める計算手順電圧の瞬時値 $...
正弦波交流電源にコイルだけ接続されている次のような回路において、この回路の電力（平均電力）$P_{av}$ を、電圧の瞬時値 $v\left( t\right)$ と電流の瞬時値 $i\left( t\right)$ から求めてみます。電力（平均電力）$P_{av}$ を求める計算手順電圧の瞬時値 ...
正弦波交流電源にコンデンサだけ接続されている次のような回路において、この回路の電力（平均電力）$P_{av}$ を、電圧の瞬時値 $v\left( t\right)$ と電流の瞬時値 $i\left( t\right)$ から求めてみます。電力（平均電力）$P_{av}$ を求める計算手順電圧の瞬時...
正弦波交流電源に抵抗とコイルが直列に接続されている次のような回路（RL直列回路）において、この回路の電力（平均電力）$P_{av}$ を、電圧の瞬時値 $v\left( t\right)$ と電流の瞬時値 $i\left( t\right)$ から求めてみます。電力（平均電力）$P_{av}$ を求...
正弦波交流電源に抵抗とコンデンサが直列に接続されている次のような回路（RC直列回路）において、この回路の電力（平均電力）$P_{av}$ を、電圧の瞬時値 $v\left( t\right)$ と電流の瞬時値 $i\left( t\right)$ から求めてみます。電力（平均電力）$P_{av}$ ...
交流回路の電力には有効電力、無効電力、皮相電力の3種類の電力があります。直流回路で電力を求めるときには電圧と電流をそのままかけるだけですが、交流回路の場合には電力が3種類もあるので、どの電力を求めるかで求める式も違います。（って、ものが違えば求める式も違うよね。）ここでは、有効電力、無効電力、皮相電...
力率って何でしょうか？交流回路の勉強をしていると力率という言葉がでてきます。力率は「力」と「率」を合わせた言葉ですが、電気の世界では、「力」は、ま〜、「電力」ですね。それから、「率」は一般的に「割合」のことを言います。つまり、力率は「電力の割合」ということになります。（ちょっと、こじつけ？）それで、...
またまた、力率って何でしょうか？力率と電力の関係については、力率とは？（力率と電力の関係）のページで解説しましたが、ここでは、力率と位相（位相差）の関係について説明します。力率は、電圧と電流の位相差を $\theta$ とすると、次のように表わされます。力率：$\cos\theta$ …①...
波形の実効値、平均値、波形率、波高率には、それぞれの値を求めるための定義式があり、対象の波形の式を $v\left( t\right)$ 、周期を $T$ とすると、それぞれ次のようになります。実効値の定義式： $V_{rms}=\sqrt{\dfrac{1}{T}\displaystyle\int...
正弦波波形の実効値、平均値、最大値、波形率、波高率を求めてみます。正弦波波形は図1のような波形になるので、この波形を与える式を$v\left( t\right) =V_m\sin\omega t$とし、波形の周期を $T$ として、実効値から順番に計算して求めてみます。正弦波波形の実効値の計算正弦波...
全波整流波形の実効値、平均値、最大値、波形率、波高率を求めてみます。全波整流波形は図1のような波形になるので、この波形を与える式を$v\left( t\right) =|V_m\sin\omega t|$とし、波形の周期を $T$ として、実効値から順番に計算して求めてみます。全波整流波形の実効値の...
半波整流波形の実効値、平均値、最大値、波形率、波高率を求めてみます。半波整流波形は図1のような波形になるので、この波形を与える式（1周期分）を$v\left( t\right) =\begin{cases} V_m\sin\omega t & \left( 0\leqq t\lt\dfrac{T}{...
方形波波形の実効値、平均値、最大値、波形率、波高率を求めてみます。次の図1のような方形波波形を考え、この波形を与える式（1周期分）を$v\left( t\right) =\begin{cases} V_m & \left( 0\leqq t\lt\dfrac{T}{2}\right) \\ -V_m...
のこぎり波（三角波）波形の実効値、平均値、最大値、波形率、波高率を求めてみます。のこぎり波波形の場合、実効値、平均値を求めるためには初めにのこぎり波波形の式を求めなければならないので、ちょっと（けっこう？）めんどくさいですよ…。次の図1のようなのこぎり波波形を考えます。（図1ののこぎり波波形の最大値...
三相電力の公式三相電力の公式は、次の①式で表わされますよね？$P_{3l}=\sqrt{3}V_lI_l\cos\theta$ …①（ $P_{3l}$：三相電力、$V_l$：線間電圧、$I_l$：線電流、$\cos\theta$：力率 ）それで、この①式は三相電...
スター結線（Y結線）の線間電圧と相電圧の関係式スター結線（Y結線）されている三相交流回路の線間電圧と相電圧の関係は、線間電圧 $=\sqrt{3} \ \times$ 相電圧 …①となり、この関係式はスター結線（Y結線）の三相交流回路を考えるときによく使われていて、ほぼ公式みたいなもので...
次の左の図のような接続をデルタ結線（$\Delta$結線）、右の図のような接続をスター結線（$\mathrm{Y}$結線）といいます。デルタ結線（$\Delta$結線）は、三角結線とも呼ばれます。また、スター結線（$\mathrm{Y}$結線）は、ワイ結線、または星形結線とも呼ばれます。このデルタ結...
次の左の図のような接続をスター結線（$\mathrm{Y}$結線）、右の図のような接続をデルタ結線（$\Delta$結線）といいます。スター結線（$\mathrm{Y}$結線）は、ワイ結線、または星形結線とも呼ばれます。また、デルタ結線（$\Delta$結線）は、三角結線とも呼ばれます。このスター結...
テブナンの定理（鳳-テブナンの定理）は等価電圧源の定理とも呼ばれ、電源を含む回路において、ある特定の素子に流れる電流を求めたいときに有用な定理です。例えば、次のような電源を含む回路があって、この回路の端子 $\mathrm{a}$-$\mathrm{b}$ 間に接続されているインピーダンス $\do...
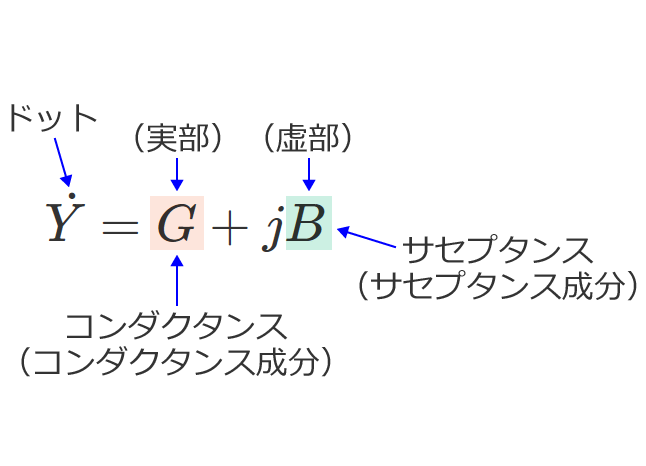
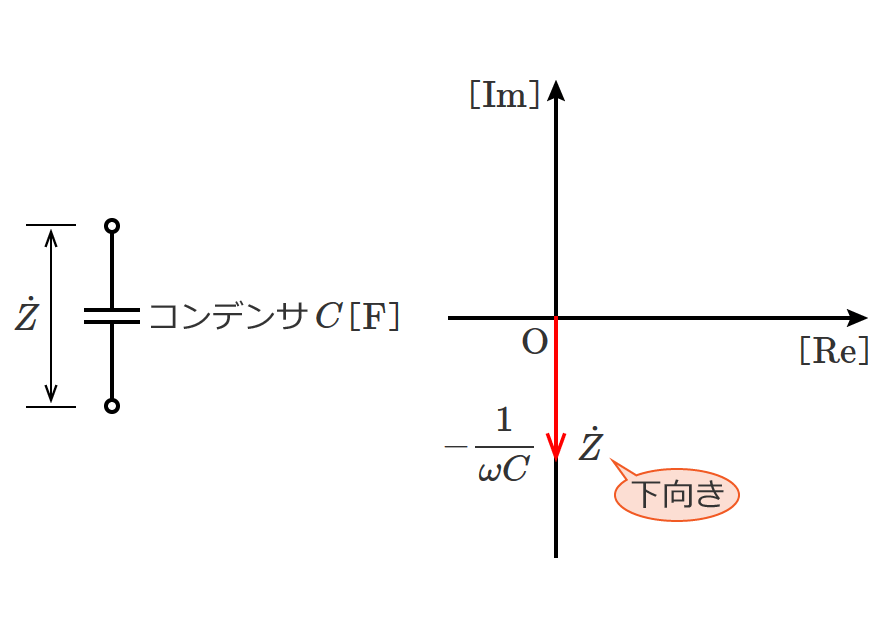
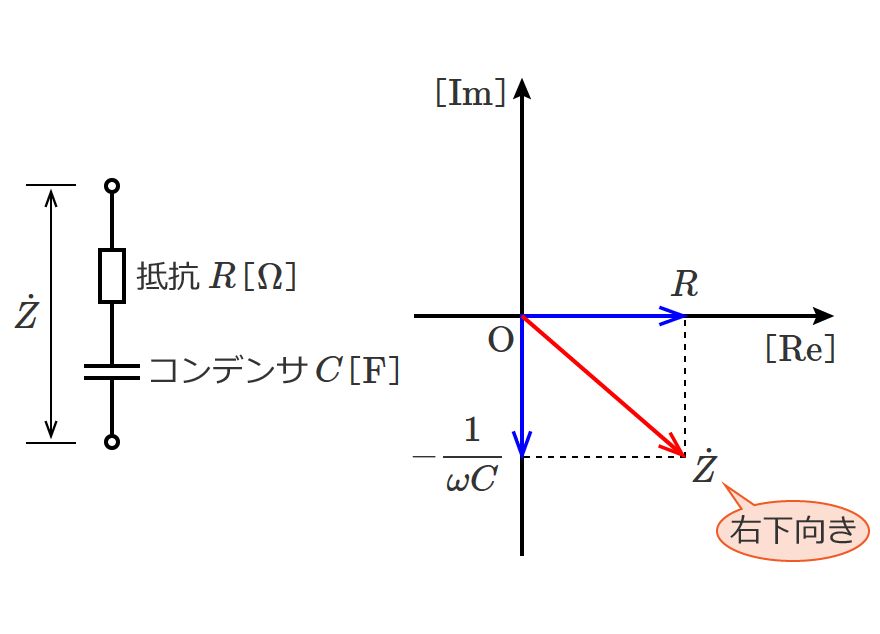
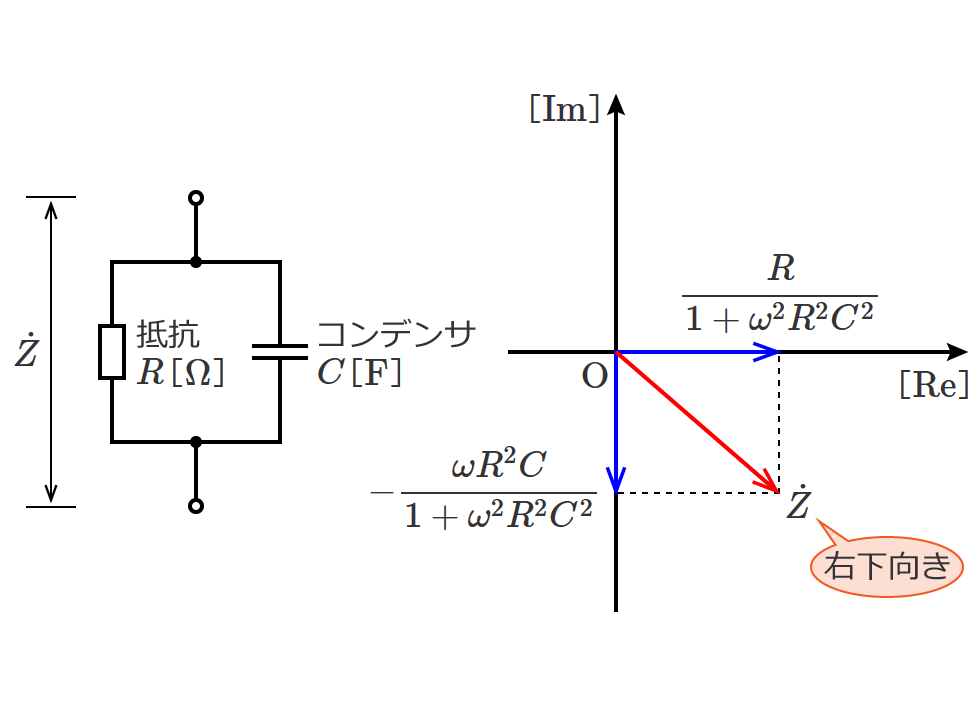
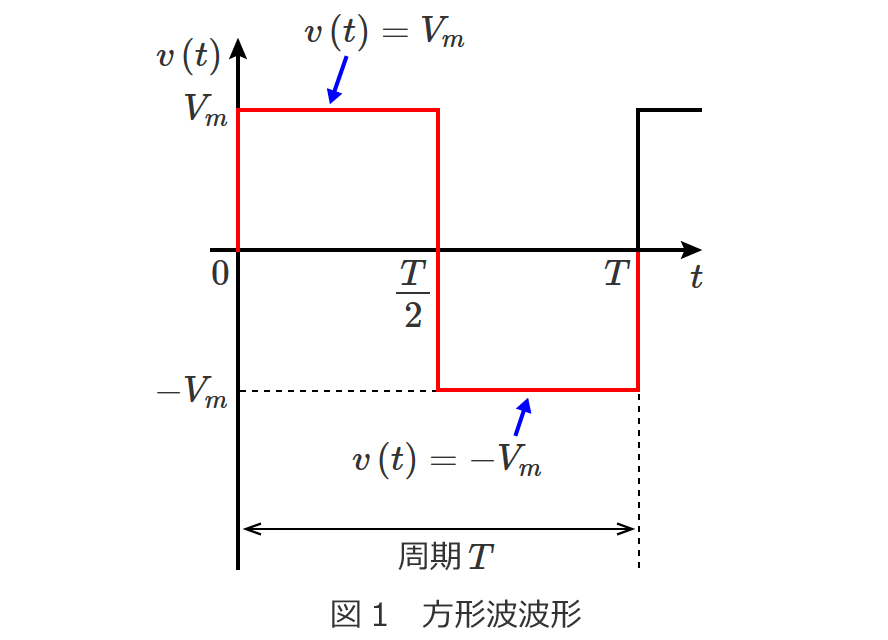
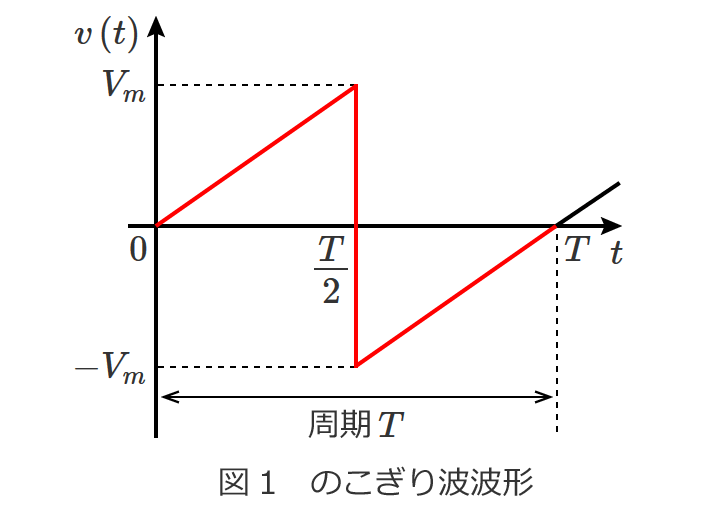
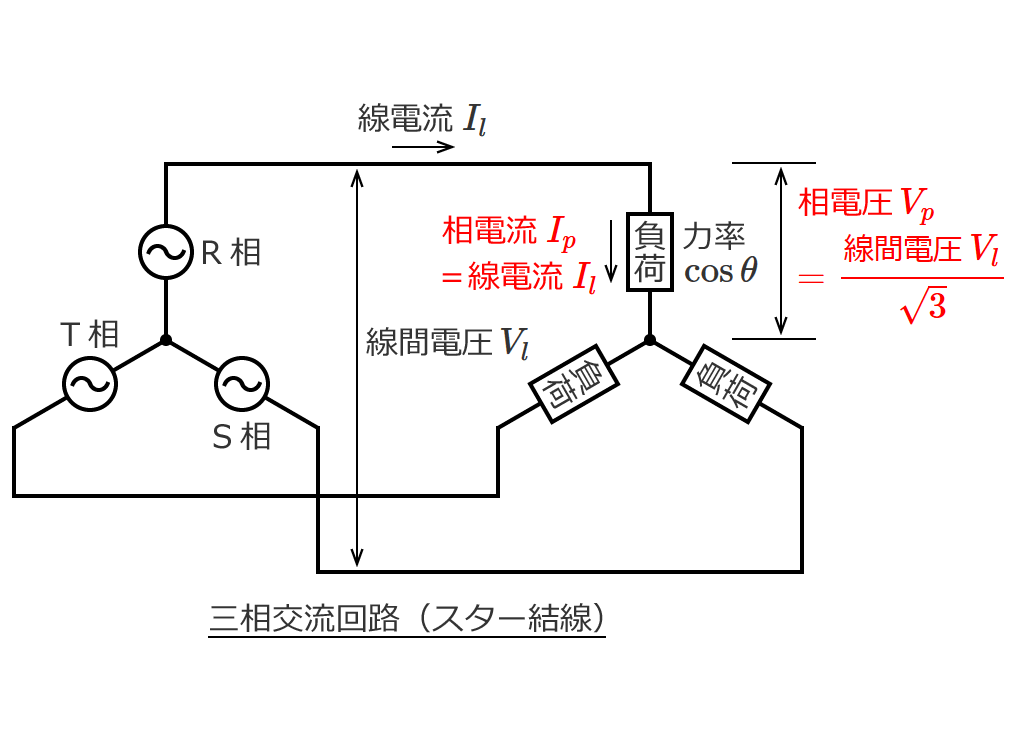
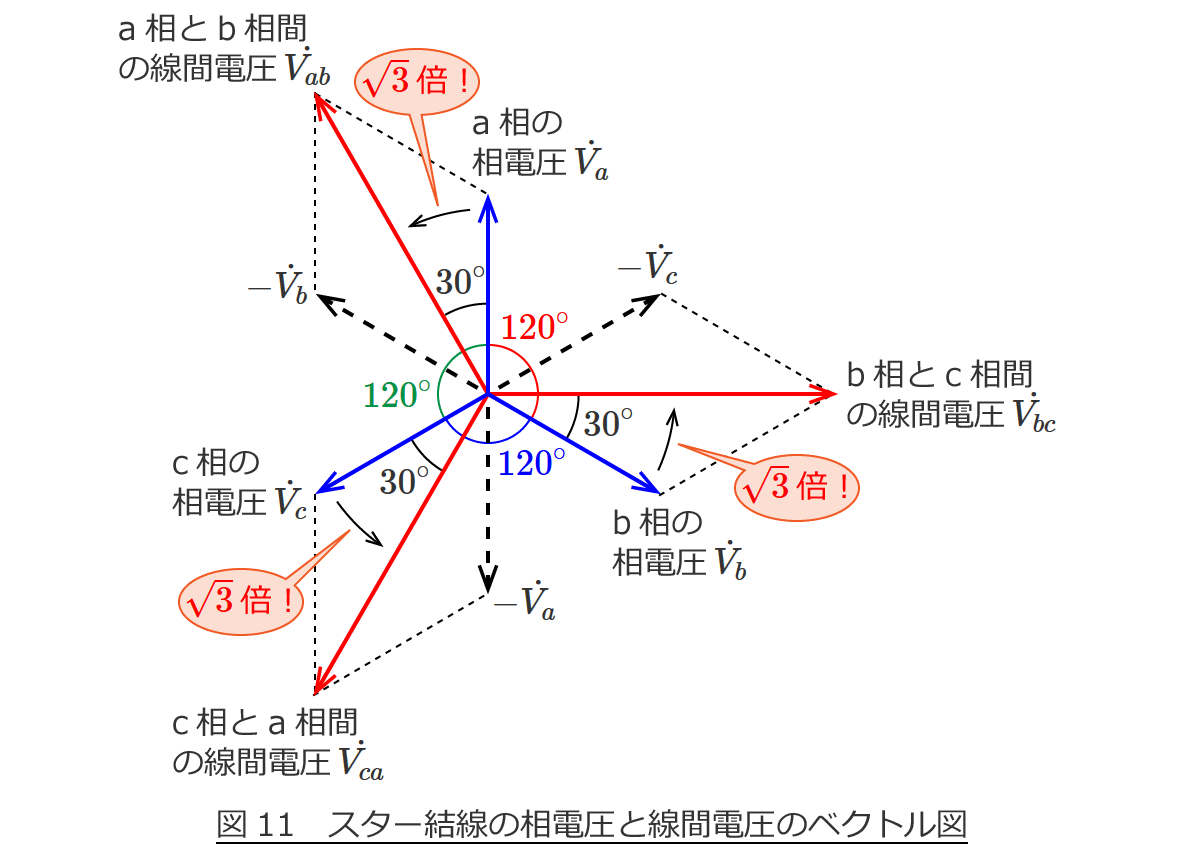
スポンサーリンク
