スポンサーリンク
テブナンの定理
※ページ内にPR・広告が含まれる場合があります。
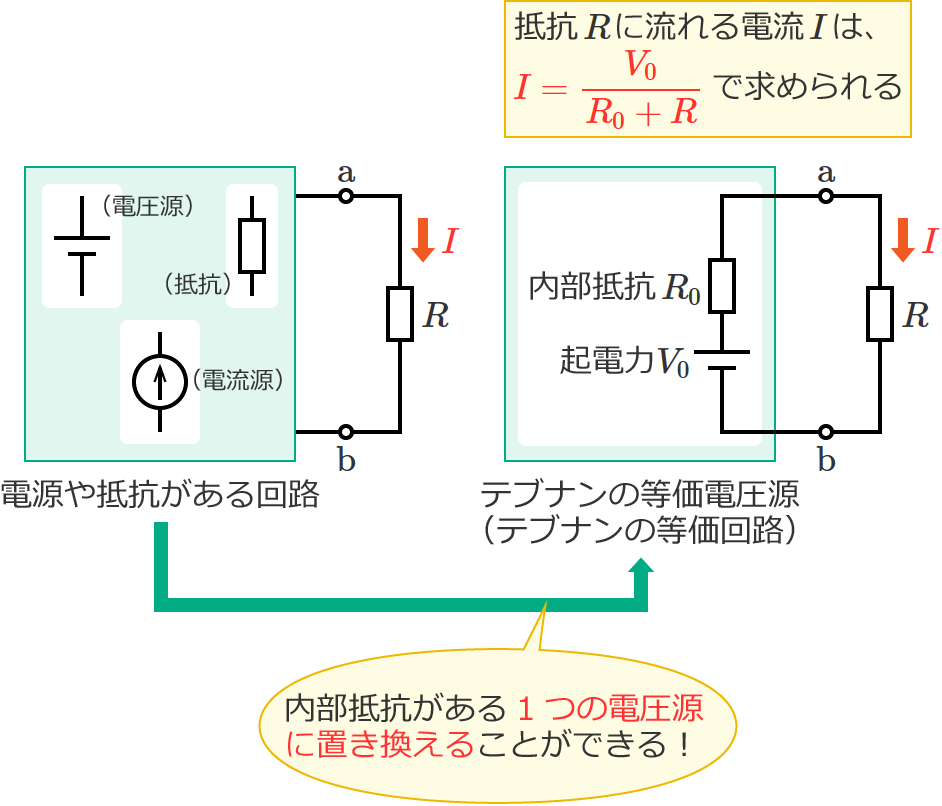
テブナンの定理(鳳-テブナンの定理)は等価電圧源の定理とも呼ばれ、電源を含む回路において、ある特定の素子に流れる電流を求めたいときに有用な定理です。
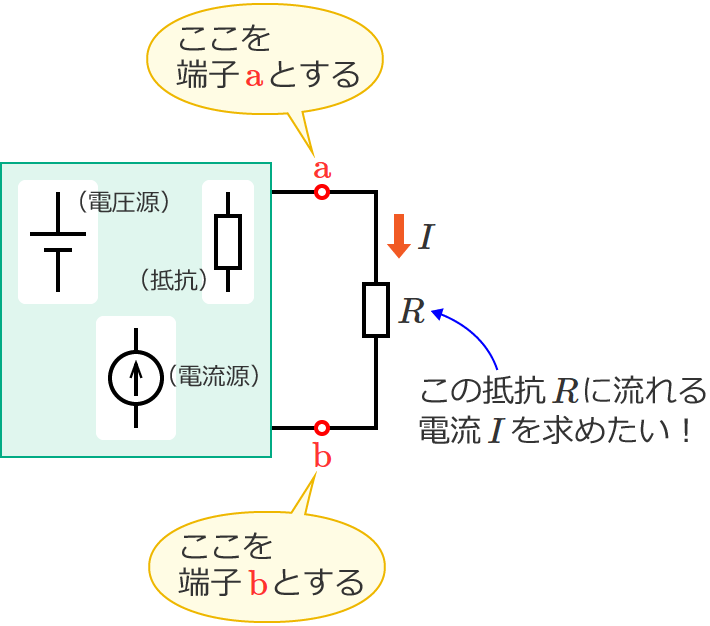
例えば、次のような電源を含む回路があって、この回路の端子 $\mathrm{a}$-$\mathrm{b}$ 間に接続されている抵抗 $R$[$\Omega$]に流れる電流 $I$[$\mathrm{A}$]を求めたいとします。
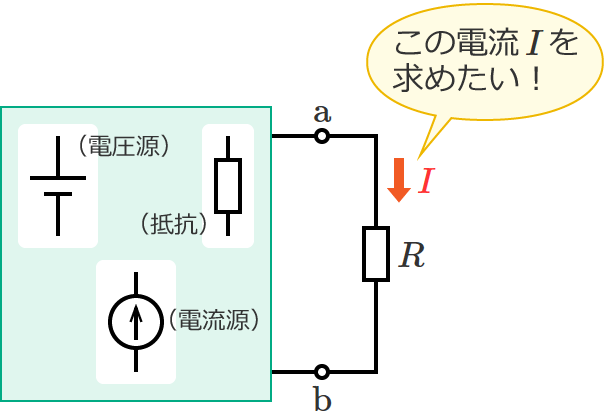
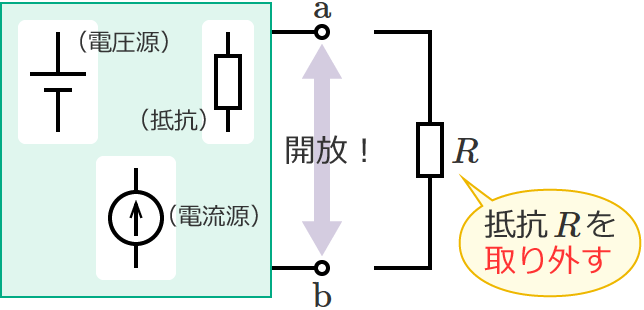
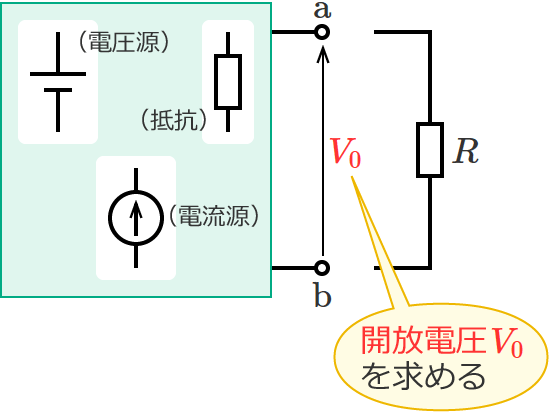
このとき、抵抗 $R$ を取り外した状態での端子 $\mathrm{a}$-$\mathrm{b}$ 間に現れる電圧(開放電圧)を $V_0$[$\mathrm{V}$]、
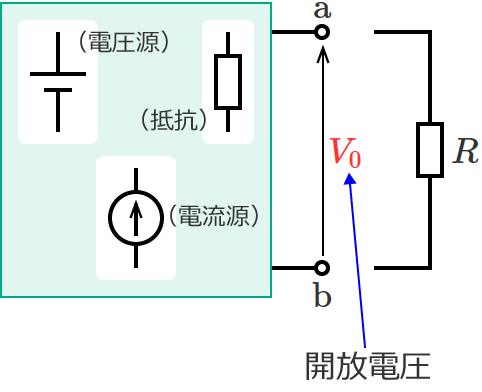
抵抗 $R$ を取り外した状態での端子 $\mathrm{a}$-$\mathrm{b}$ 間の合成抵抗を $R_0$[$\Omega$]とすると、
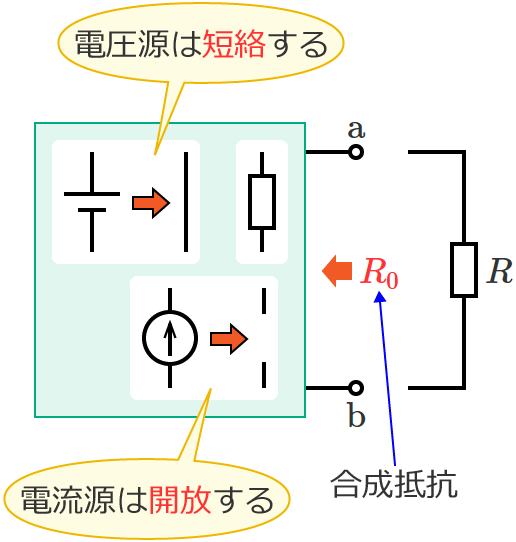
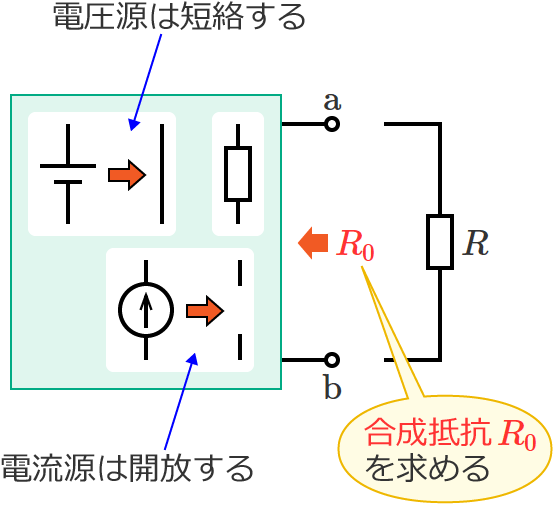
端子 $\mathrm{a}$-$\mathrm{b}$ 間の合成抵抗 $R_0$ を求めるときは、電圧源は短絡、電流源は開放します。
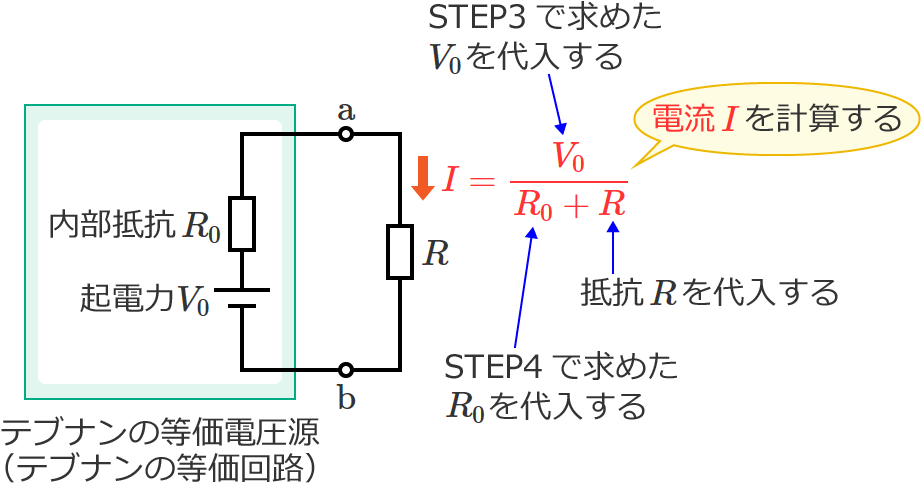
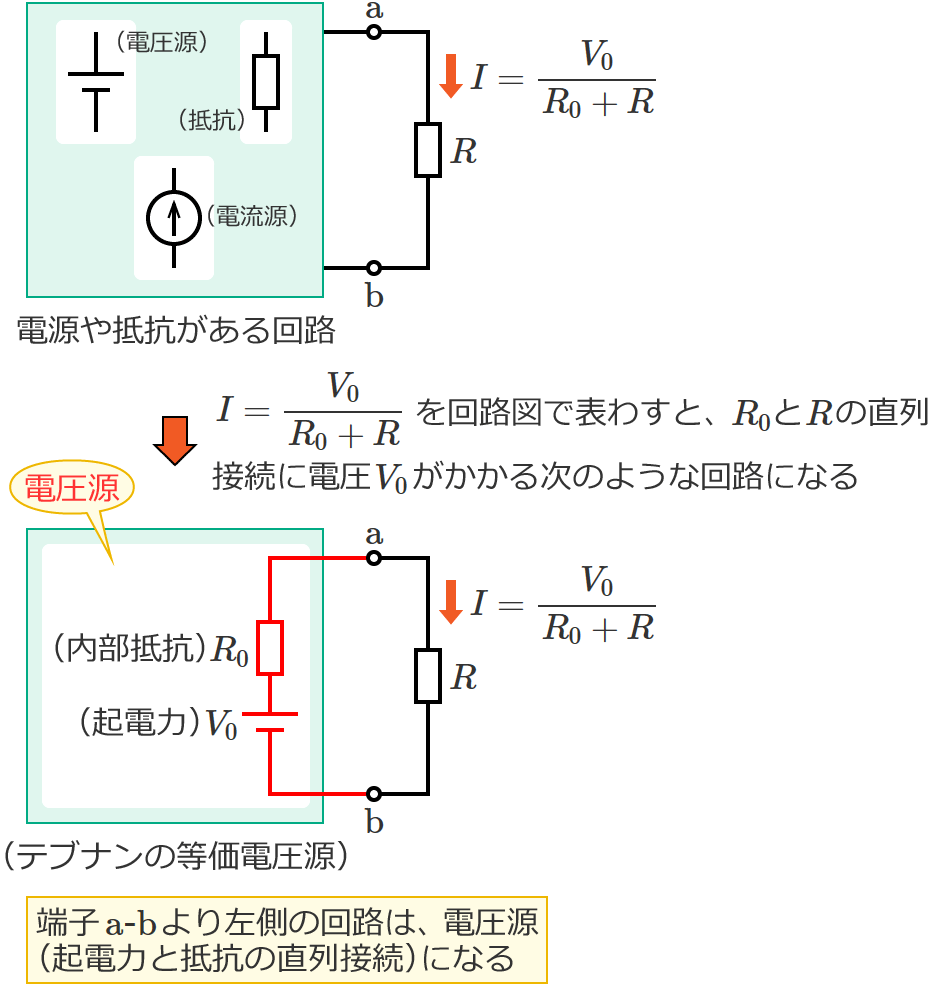
端子 $\mathrm{a}$-$\mathrm{b}$ より左側の回路は、起電力が $V_0$ で内部抵抗が $R_0$ の電圧源に置き換える(等価変換する)ことができ、
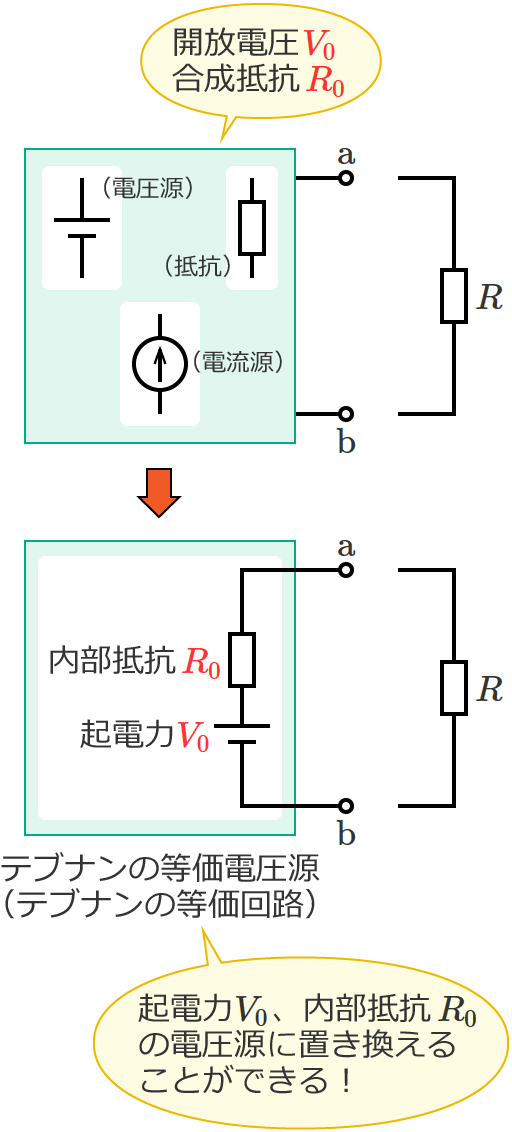
この置き換えた電圧源を、テブナンの等価電圧源とか、テブナンの等価回路といいます。
抵抗 $R$ に流れる電流 $I$ は、次の式で求めることができます。
$I=\dfrac{V_0}{R_0+R}$ …① (テブナンの定理の式)
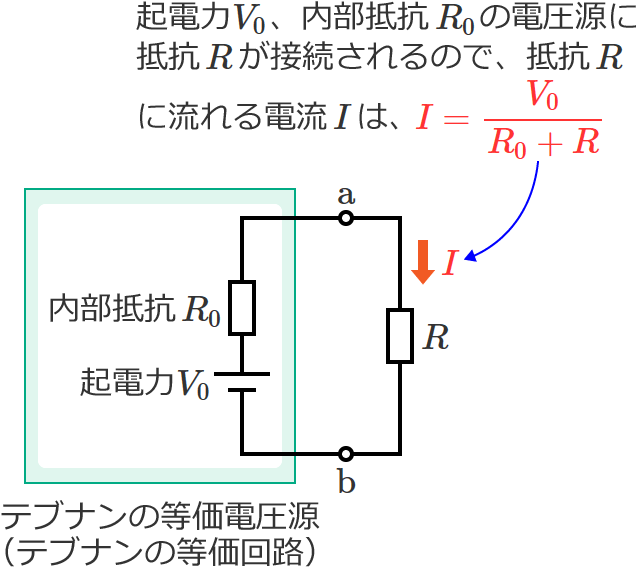
これがテブナンの定理で、テブナンの定理を使うと、電流を求めたいところの特定の素子を除いた部分の回路(この場合、端子 $\mathrm{a}$-$\mathrm{b}$ より左側の回路)を内部抵抗がある1つの電圧源で等価的に置き換えることができるので、複雑な回路であっても回路を単純化して電流の計算をできるようになります。
スポンサーリンク
テブナンの定理による電流の求め方を整理すると、次のような手順(STEP1〜STEP5)になります。
STEP3とSTEP4の順番は逆でもかまいません。
以上のような手順で、抵抗 $R$ に流れる電流 $I$ を求めることができます。
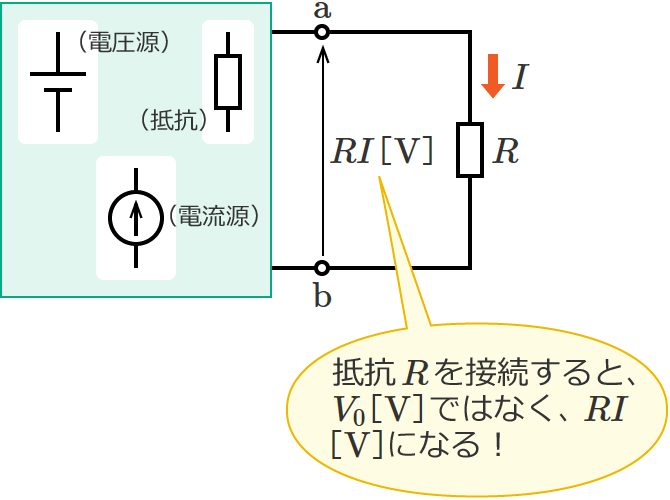
ちなみにちょっと補足すると、STEP3で求めた開放電圧は $V_0$[$\mathrm{V}$]ですが、この電圧 $V_0$[$\mathrm{V}$]は抵抗 $R$ を接続して抵抗 $R$ に電流が流れている状態での抵抗 $R$ の両端にかかる電圧(=端子 $\mathrm{a}$-$\mathrm{b}$ 間の電圧)とは異なります。抵抗 $R$ を接続して抵抗 $R$ に電流が流れている状態での抵抗 $R$ にかかる電圧は、$V_0$[$\mathrm{V}$]ではなく $RI$[$\mathrm{V}$]になるので注意しましょう。
では続いて、テブナンの定理の問題でよくある回路を例にして、抵抗に流れる電流を求めてみましょう。
いくつか計算してみるとテブナンの定理に慣れてきて、計算のやり方をおぼえられるようになりますよ!
このページではテブナンの定理を直流回路(電源は直流電源、素子は抵抗のみ)で解説していますが、テブナンの定理は交流回路でも成り立つ定理です。交流回路のテブナンの定理については、こちらの交流回路のテブナンの定理のページを参考にしてみてください。
スポンサーリンク
スポンサーリンク
テブナンの定理による電流の計算
ここでは、
- 電源が1つ、抵抗が3つある回路
- 電源が2つ、抵抗が3つある回路
- ブリッジ回路
の3つの回路について、テブナンの定理を用いて抵抗に流れる電流を求めてみます。
電源が1つ、抵抗が3つある回路
テブナンの定理を用いて、次の回路の抵抗 $R_3$ に流れる電流 $I$ を先ほどのSTEP1〜5の手順に従って求めてみます。
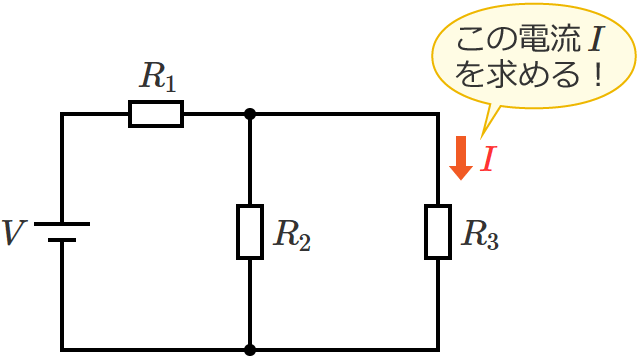
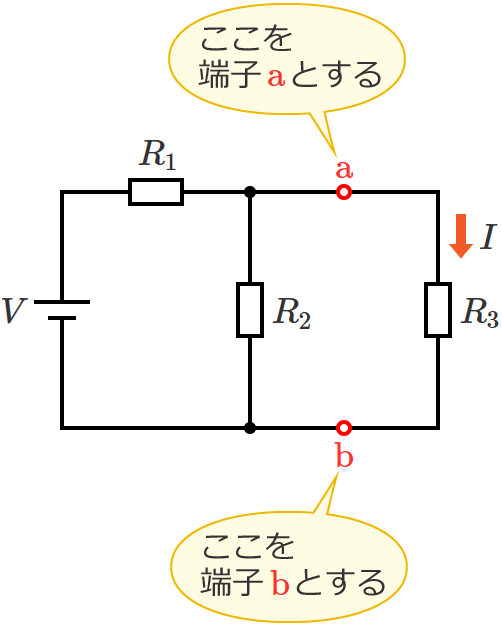
抵抗 $R_3$ に流れる電流を求めたいので、抵抗 $R_3$ の両端を端子「$\mathrm{a}$」「$\mathrm{b}$」とします。
抵抗 $R_3$ を取り外して、端子 $\mathrm{a}$-$\mathrm{b}$ 間を開放状態にします。
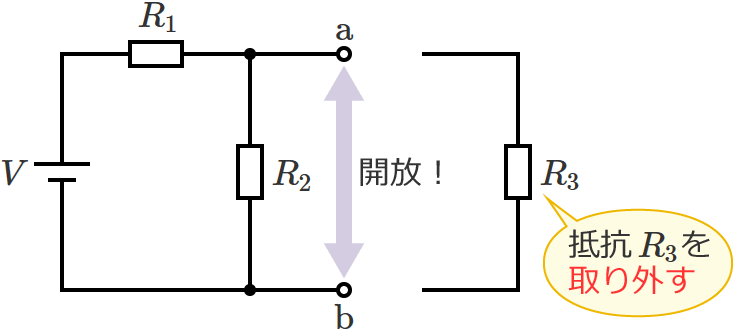
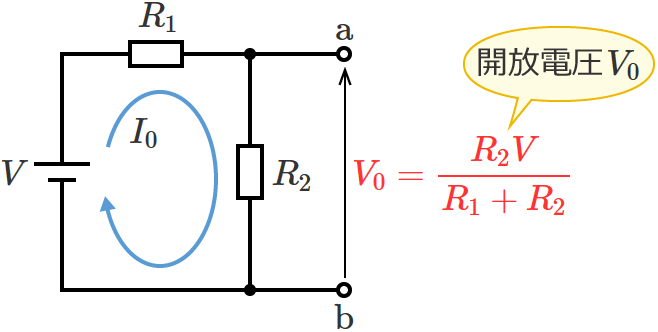
抵抗 $R_3$ を取り外したときの回路は、次のように電圧 $V$[$\mathrm{V}$]の電源に $R_1$[$\Omega$]と$R_2$[$\Omega$]の抵抗が直列接続された回路になるので、
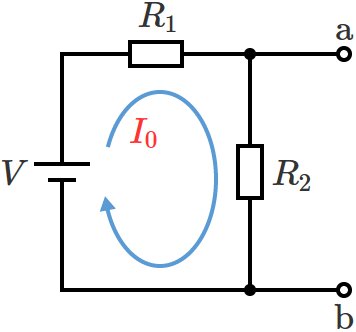
この回路に流れる電流 $I_0$[$\mathrm{A}$]はオームの法則より、
$I_0=\dfrac{V}{R_1+R_2}$
となります。なので、端子 $\mathrm{a}$-$\mathrm{b}$ 間の電圧(開放電圧)$V_0$ はオームの法則より、
$V_0=R_2I_0=R_2\times\dfrac{V}{R_1+R_2}$
$\therefore V_0=\dfrac{R_2V}{R_1+R_2}$ (開放電圧 $V_0$ )
となります。
ちなみに、端子 $\mathrm{a}$-$\mathrm{b}$ 間の電圧(開放電圧)$V_0$ は、分圧の公式を使って、
$V_0=V\times\dfrac{R_2}{R_1+R_2}$
$\therefore V_0=\dfrac{R_2V}{R_1+R_2}$ (開放電圧 $V_0$ )
と求めることもできます。
電圧源は短絡し、電流源は開放して回路内のすべての電源を取り除くと、回路は次のようになります。
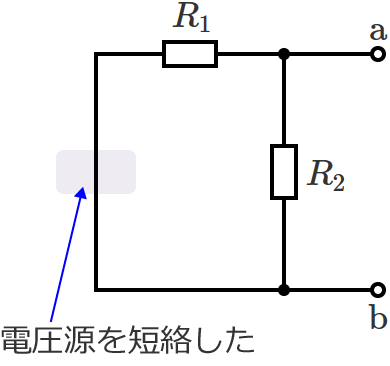
この回路の電源は電圧源だけなので、電圧源を短絡します。
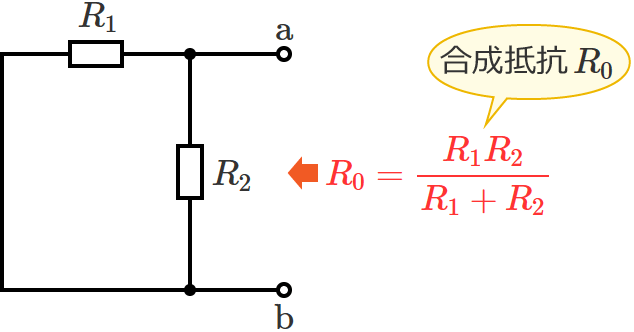
電源を取り除くと抵抗 $R_1$ と抵抗 $R_2$ が並列に接続された回路になっているので、端子 $\mathrm{a}$-$\mathrm{b}$ からみた回路の合成抵抗 $R_0$ は和分の積で、
$\therefore R_0=\dfrac{R_1R_2}{R_1+R_2}$ (合成抵抗 $R_0$ )
となります。
STEP3で求めた開放電圧 $V_0$ とSTEP4で求めた合成抵抗 $R_0$ は、
$V_0=\dfrac{R_2V}{R_1+R_2}$
$R_0=\dfrac{R_1R_2}{R_1+R_2}$
で、端子 $\mathrm{a}$-$\mathrm{b}$ 間の抵抗は $R_3$ なので、これらをテブナンの定理の式(①式)に代入すると、
$I=\dfrac{V_0}{R_0+R_3} =\dfrac{\dfrac{R_2V}{R_1+R_2}}{\dfrac{R_1R_2}{R_1+R_2} +R_3}$
$=\dfrac{\dfrac{R_2V}{R_1+R_2}}{\dfrac{R_1R_2+R_3\left( R_1+R_2\right)}{R_1+R_2}}$
$=\dfrac{R_2V}{R_1R_2+R_3R_1+R_3R_2}$
$\therefore I=\dfrac{R_2V}{R_1R_2+R_2R_3+R_3R_1}$ (抵抗 $R_3$ に流れる電流 $I$ )
となり、この電流 $I$ が抵抗 $R_3$ に流れる電流になります。
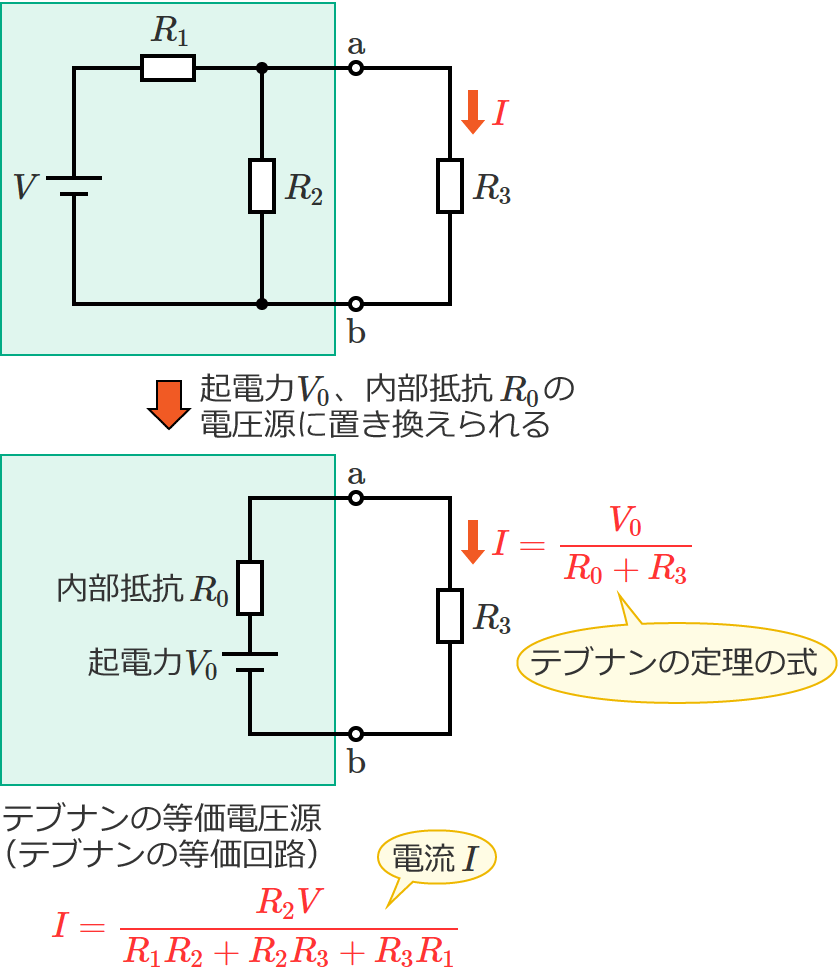
以上で、「電源が1つ、抵抗が3つある回路」の抵抗 $R_3$ に流れる電流 $I$ が求められました。
この回路は複雑な回路ではないので、そんなに難しくはないですね。
次は、電源が2つある回路の計算です。電源が2つあるのでちょっとだけ難しくなりますよ、ちょっとだけ。
電源が2つ、抵抗が3つある回路
テブナンの定理を用いて、次の回路の抵抗 $R_3$ に流れる電流 $I$ を求めてみます。
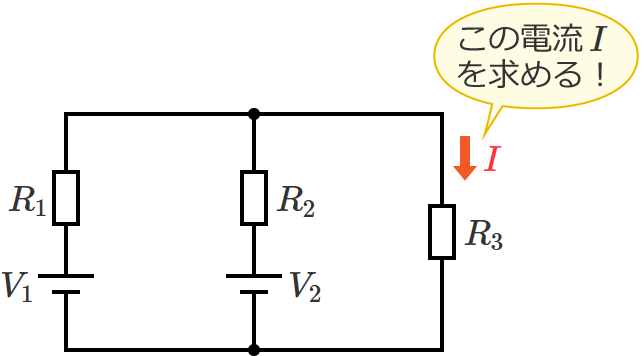
抵抗 $R_3$ に流れる電流を求めたいので、抵抗 $R_3$ の両端を端子「$\mathrm{a}$」「$\mathrm{b}$」とします。
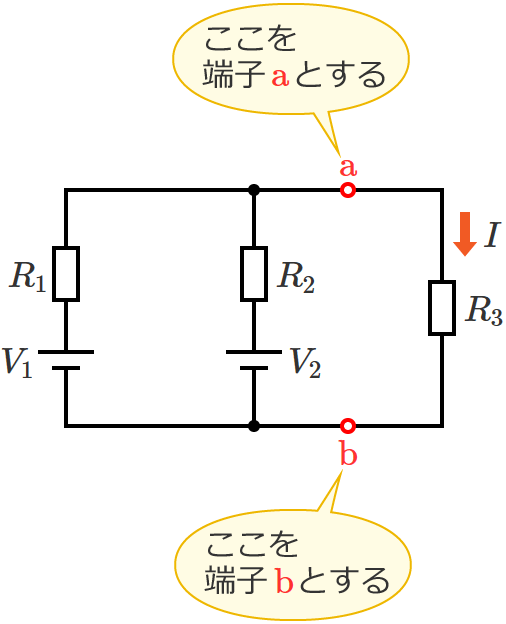
抵抗 $R_3$ を取り外して、端子 $\mathrm{a}$-$\mathrm{b}$ 間を開放状態にします。
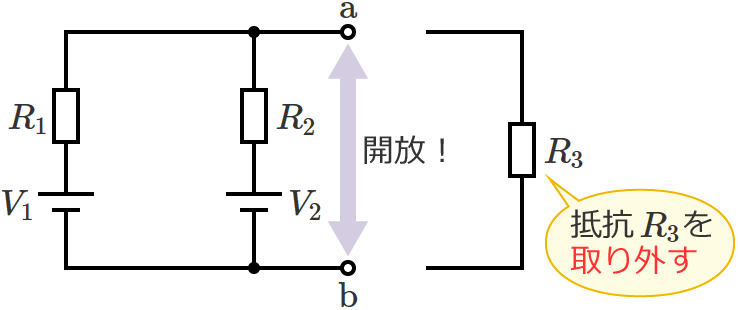
抵抗 $R_3$ を取り外したときの回路はSTEP2より次のようになり、この回路において、次のように右回り(時計回り)の電流 $I_0$ が流れるものと仮定すると、
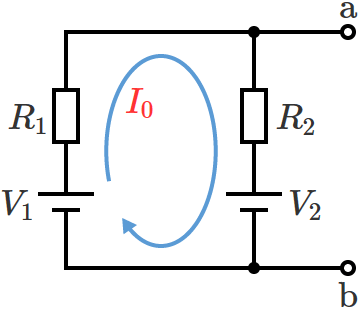
キルヒホッフの法則(キルヒホッフの第二法則)より、電流 $I_0$ は次のようになります。
$V_1-V_2=R_1I_0+R_2I_0$ (キルヒホッフの第二法則より)
$V_1-V_2=\left( R_1+R_2\right) I_0$
$\therefore I_0=\dfrac{V_1-V_2}{R_1+R_2}$
したがって、抵抗 $R_1$ での電圧降下は $R_1I_0=\dfrac{R_1\left( V_1-V_2\right)}{R_1+R_2}$[$\mathrm{V}$]となるので、端子 $\mathrm{a}$-$\mathrm{b}$ 間の電圧(開放電圧)$V_0$ は、
$V_0=V_1-R_1I_0$ …②
$=V_1-\dfrac{R_1\left( V_1-V_2\right)}{R_1+R_2}$
$=\dfrac{V_1\left( R_1+R_2\right) -R_1\left( V_1-V_2\right)}{R_1+R_2}$
$=\dfrac{R_1V_1+R_2V_1-R_1V_1+R_1V_2}{R_1+R_2}$
$=\dfrac{R_2V_1+R_1V_2}{R_1+R_2}$
$\therefore V_0=\dfrac{R_2V_1+R_1V_2}{R_1+R_2}$ (開放電圧 $V_0$ )
となります。
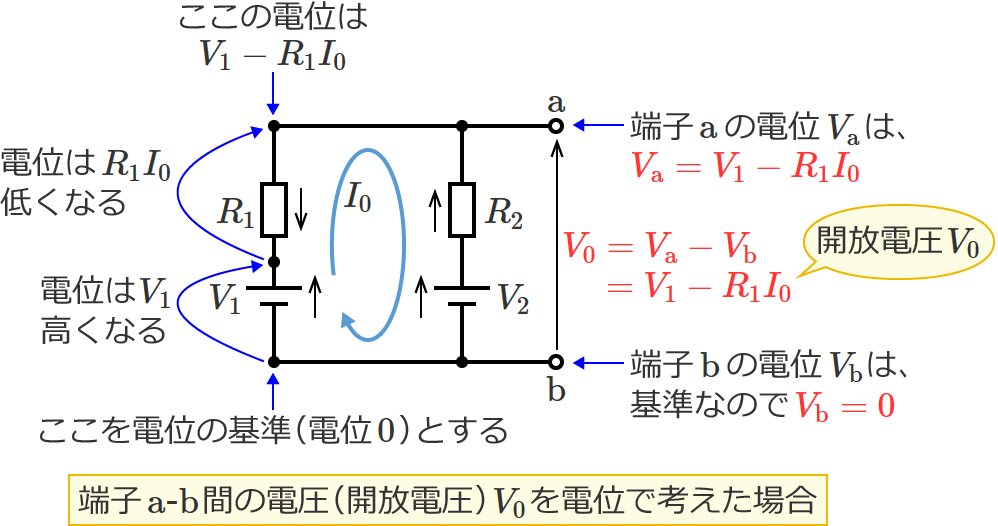
ちなみに、②式( $V_0=V_1-R_1I_0$ )は「 $V_1$ と $R_1$ の直列接続側」で考えた場合の式ですが、「 $V_2$ と $R_2$ の直列接続側」で考えた場合は次の③式のようになります。(どちら側で考えても、計算結果は同じになります。)
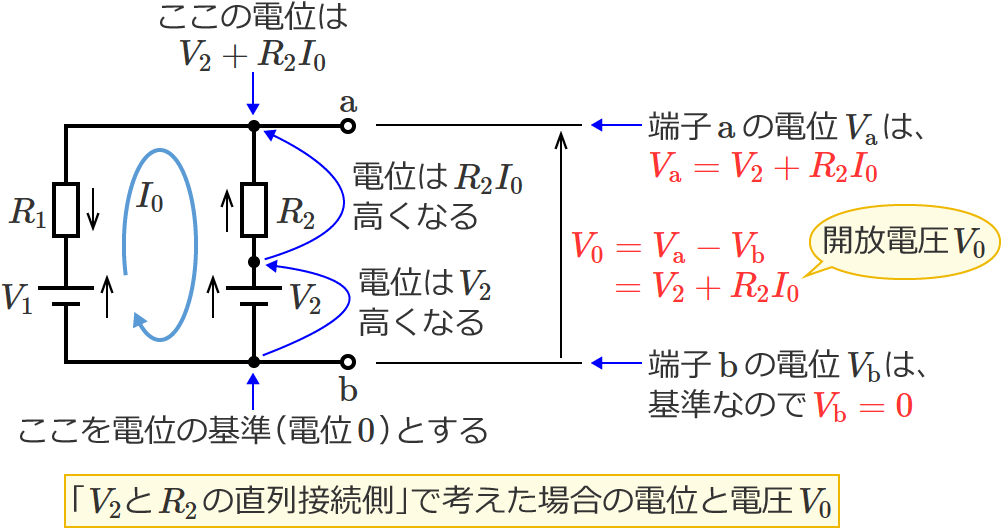
$V_0=V_2+R_2I_0$ …③
$=V_2+R_2\cdot\dfrac{V_1-V_2}{R_1+R_2}$
$=V_2+\dfrac{R_2\left( V_1-V_2\right)}{R_1+R_2}$
$=\dfrac{V_2\left( R_1+R_2\right) +R_2\left( V_1-V_2\right)}{R_1+R_2}$
$=\dfrac{R_1V_2+R_2V_2+R_2V_1-R_2V_2}{R_1+R_2}$
$=\dfrac{R_1V_2+R_2V_1}{R_1+R_2}$
$\therefore V_0=\dfrac{R_2V_1+R_1V_2}{R_1+R_2}$ (開放電圧 $V_0$ )
電圧源は短絡し、電流源は開放して回路内のすべての電源を取り除くと、回路は次のようになります。
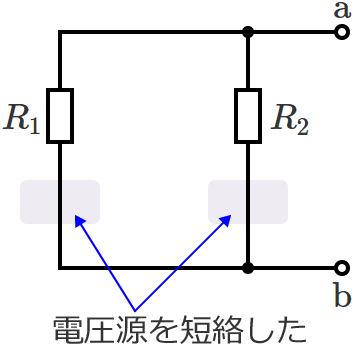
この回路の電源は電圧源だけなので、電圧源を短絡します。
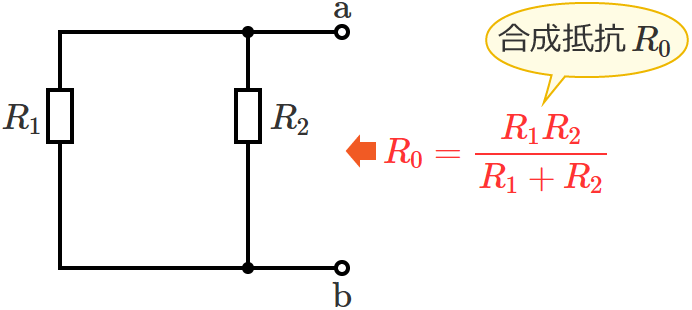
電源を取り除くと抵抗 $R_1$ と抵抗 $R_2$ が並列に接続された回路になっているので、端子 $\mathrm{a}$-$\mathrm{b}$ からみた回路の合成抵抗 $R_0$ は和分の積で、
$\therefore R_0=\dfrac{R_1R_2}{R_1+R_2}$ (合成抵抗 $R_0$ )
となります。
STEP3で求めた開放電圧 $V_0$ とSTEP4で求めた合成抵抗 $R_0$ は、
$V_0=\dfrac{R_2V_1+R_1V_2}{R_1+R_2}$
$R_0=\dfrac{R_1R_2}{R_1+R_2}$
で、端子 $\mathrm{a}$-$\mathrm{b}$ 間の抵抗は $R_3$ なので、これらをテブナンの定理の式(①式)に代入すると、
$I=\dfrac{V_0}{R_0+R_3} =\dfrac{\dfrac{R_2V_1+R_1V_2}{R_1+R_2}}{\dfrac{R_1R_2}{R_1+R_2} +R_3}$
$=\dfrac{\dfrac{R_2V_1+R_1V_2}{R_1+R_2}}{\dfrac{R_1R_2+R_3\left( R_1+R_2\right)}{R_1+R_2}}$
$=\dfrac{R_2V_1+R_1V_2}{R_1R_2+R_3R_1+R_3R_2}$
$\therefore I=\dfrac{R_2V_1+R_1V_2}{R_1R_2+R_2R_3+R_3R_1}$ (抵抗 $R_3$ に流れる電流 $I$ )
となり、この電流 $I$ が抵抗 $R_3$ に流れる電流になります。
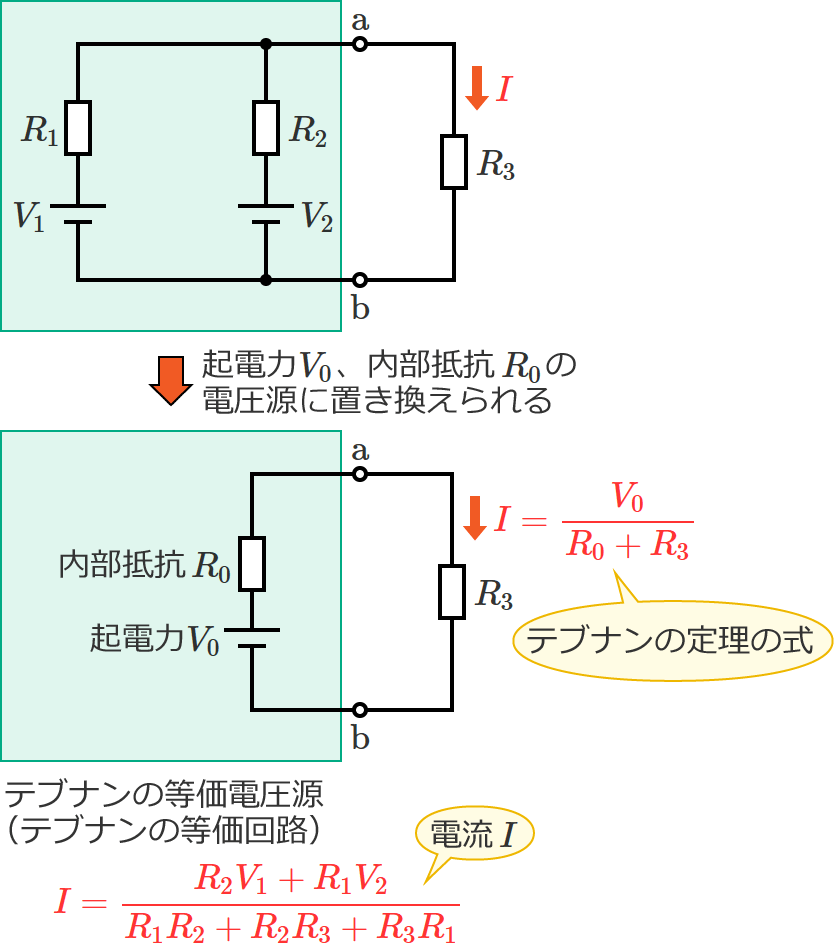
以上で、「電源が2つ、抵抗が3つある回路」の抵抗 $R_3$ に流れる電流 $I$ が求められました。
次は、ブリッジ回路の計算です。解き方はそんなに難しくないのですが、抵抗の数が増えるので式が少し複雑になります。
ブリッジ回路
テブナンの定理を用いて、次のブリッジ回路の抵抗 $R_5$ に流れる電流 $I$ を求めてみます。
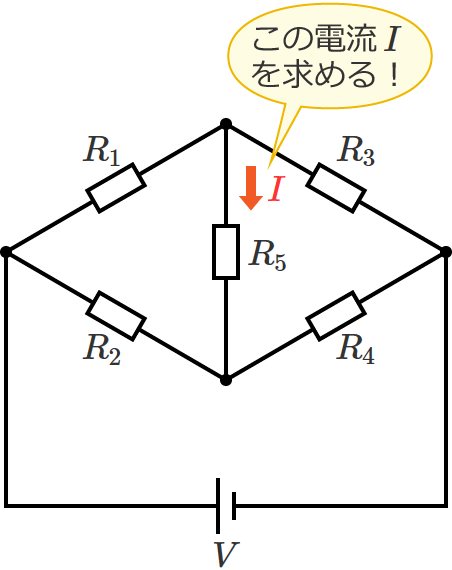
抵抗 $R_5$ に流れる電流を求めたいので、抵抗 $R_5$ の両端を端子「$\mathrm{a}$」「$\mathrm{b}$」とします。
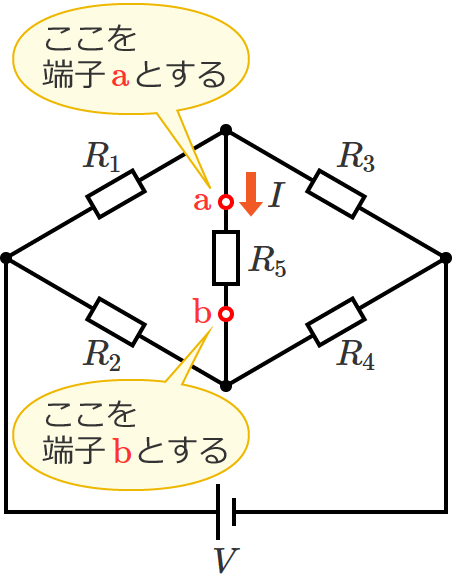
抵抗 $R_5$ を取り外して、端子 $\mathrm{a}$-$\mathrm{b}$ 間を開放状態にします。
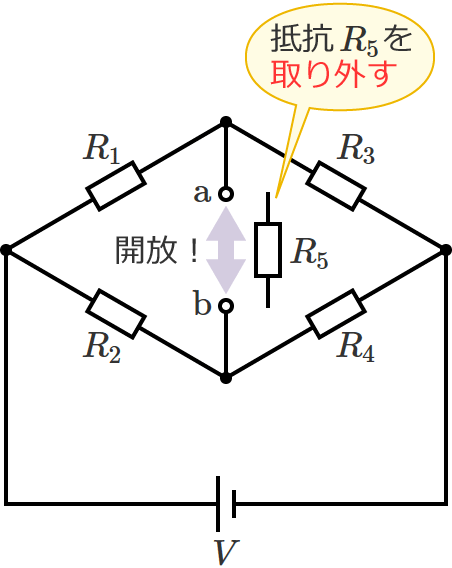
抵抗 $R_5$ を取り外したときの回路はSTEP2より次のようになります。
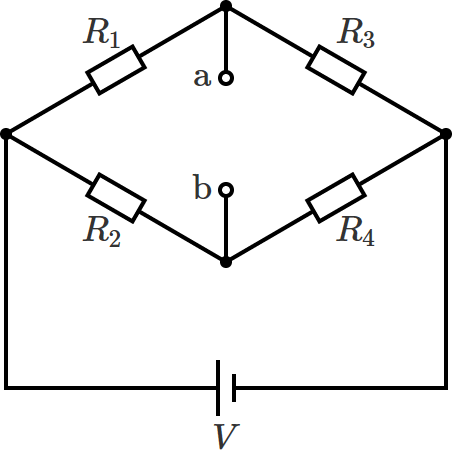
この回路において、電源のマイナス側を電位の基準(電位 $0\,\mathrm{V}$ )とし、端子 $\mathrm{a}$ での電位を $V_{\mathrm{a}}$[$\mathrm{V}$]、端子 $\mathrm{b}$ での電位を $V_{\mathrm{b}}$[$\mathrm{V}$]とすると、
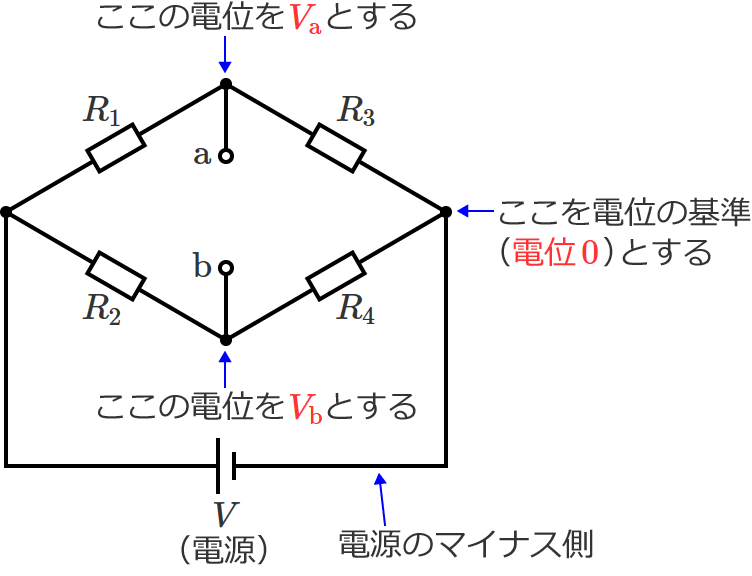
電位 $V_{\mathrm{a}}$ と電位 $V_{\mathrm{b}}$ は、それぞれ次のようになります。
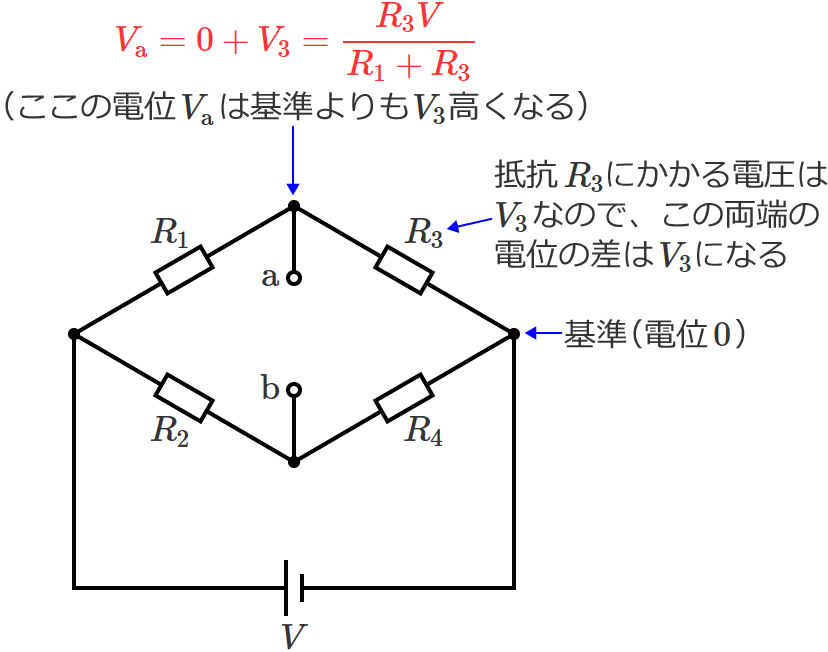
電位 $V_{\mathrm{a}}$
電源電圧 $V$ が抵抗 $R_1$ と抵抗 $R_3$ に分圧されるので、分圧の公式より抵抗 $R_3$ にかかる電圧 $V_3$[$\mathrm{V}$]を求めると、
$V_3=V\times\dfrac{R_3}{R_1+R_3}$ (分圧の公式より)
$\therefore V_3=\dfrac{R_3V}{R_1+R_3}$
となります。したがって、電源のマイナス側を電位の基準(電位 $0\,\mathrm{V}$ )としたときの電位 $V_{\mathrm{a}}$ は、次のようになります。
$V_{\mathrm{a}} =0+V_3=\dfrac{R_3V}{R_1+R_3}$
$\therefore V_{\mathrm{a}} =\dfrac{R_3V}{R_1+R_3}$ …④ (電位 $V_{\mathrm{a}}$ )
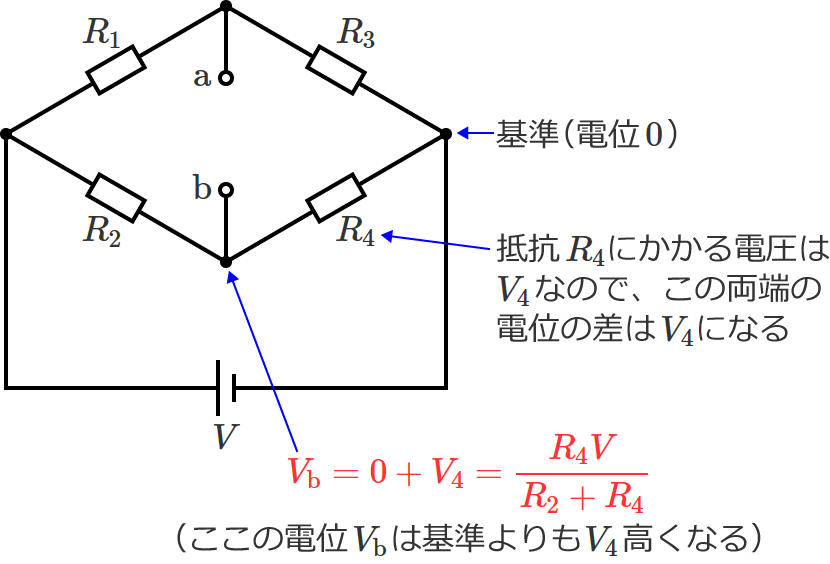
電位 $V_{\mathrm{b}}$
電源電圧 $V$ が抵抗 $R_2$ と抵抗 $R_4$ に分圧されるので、分圧の公式より抵抗 $R_4$ にかかる電圧 $V_4$[$\mathrm{V}$]を求めると、
$V_4=V\times\dfrac{R_4}{R_2+R_4}$ (分圧の公式より)
$\therefore V_4=\dfrac{R_4V}{R_2+R_4}$
となります。したがって、電源のマイナス側を電位の基準(電位 $0\,\mathrm{V}$ )としたときの電位 $V_{\mathrm{b}}$ は、次のようになります。
$V_{\mathrm{b}} =0+V_4=\dfrac{R_4V}{R_2+R_4}$
$\therefore V_{\mathrm{b}} =\dfrac{R_4V}{R_2+R_4}$ …⑤ (電位 $V_{\mathrm{b}}$ )
以上で求めた $V_{\mathrm{a}}$ と $V_{\mathrm{b}}$ の電位差 $V_{\mathrm{a}} -V_{\mathrm{b}}$ が端子 $\mathrm{a}$-$\mathrm{b}$ 間の電圧(開放電圧)$V_0$ になるので、端子 $\mathrm{a}$-$\mathrm{b}$ 間の電圧(開放電圧)$V_0$ は、
$V_0=V_{\mathrm{a}} -V_{\mathrm{b}}$
$=\dfrac{R_3V}{R_1+R_3} -\dfrac{R_4V}{R_2+R_4}$
$=\dfrac{R_3\left( R_2+R_4\right) -R_4\left( R_1+R_3\right)}{\left( R_1+R_3\right) \left( R_2+R_4\right)} V$
$=\dfrac{R_2R_3+R_3R_4-R_1R_4-R_3R_4}{\left( R_1+R_3\right) \left( R_2+R_4\right)} V$
$=\dfrac{R_2R_3-R_1R_4}{\left( R_1+R_3\right) \left( R_2+R_4\right)} V$
$\therefore V_0=\dfrac{R_2R_3-R_1R_4}{\left( R_1+R_3\right) \left( R_2+R_4\right)} V$ (開放電圧 $V_0$ )
となります。
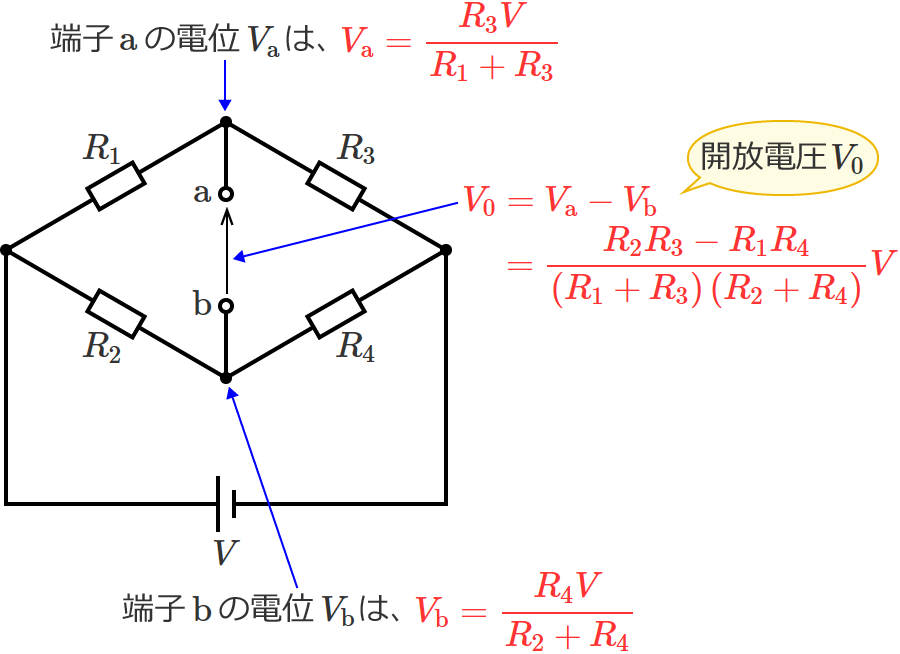
電位と電位の差が電位差、つまり電圧になります。電位と電位差については、こちらの電位と電位差のページを参考にしてみてください。
電圧源は短絡し、電流源は開放して回路内のすべての電源を取り除くと、回路は次のようになります。
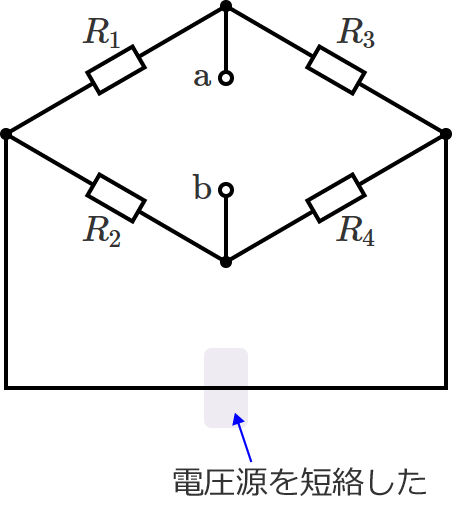
この回路の電源は電圧源だけなので、電圧源を短絡します。
このままの回路だとちょっと分かりにくいので、回路が分かりやすくなるように変形します。
まず、端子 $\mathrm{a}$ を上に、端子 $\mathrm{b}$ を下に移動します。
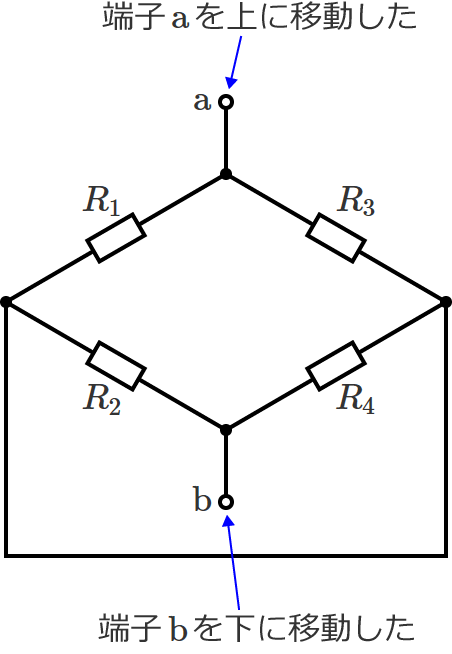
回路の両端を短絡している線(もともと電源があったところ)を、次のようにまっすぐにします。
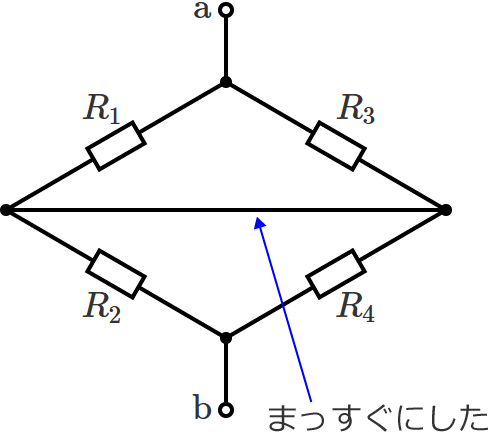
もうちょっと見やすくします。
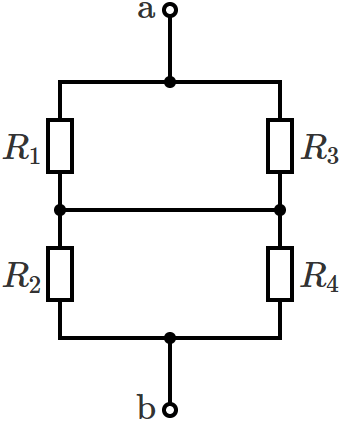
抵抗の接続が分かりやすくなるように真中の短絡されているところを描き直すと、回路は次のようになります。
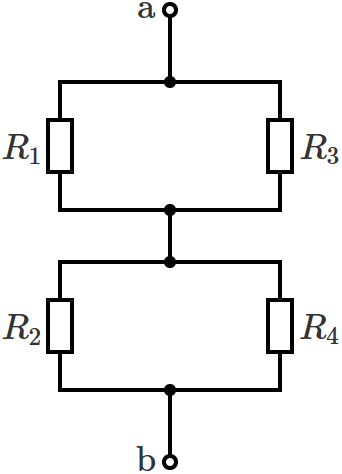
この図より回路は、「抵抗 $R_1$ と抵抗 $R_3$ の並列接続」と「抵抗 $R_2$ と抵抗 $R_4$ の並列接続」が直列に接続された回路になっているので、端子 $\mathrm{a}$-$\mathrm{b}$ からみた回路の合成抵抗 $R_0$ は、
$R_0=\dfrac{R_1R_3}{R_1+R_3} +\dfrac{R_2R_4}{R_2+R_4}$
$=\dfrac{R_1R_3\left( R_2+R_4\right) +R_2R_4\left( R_1+R_3\right)}{\left(R_1+R_3\right)\left(R_2+R_4\right)}$
$\therefore R_0=\dfrac{R_1R_3\left( R_2+R_4\right) +R_2R_4\left( R_1+R_3\right)}{\left(R_1+R_3\right)\left(R_2+R_4\right)}$ (合成抵抗 $R_0$ )
となります。
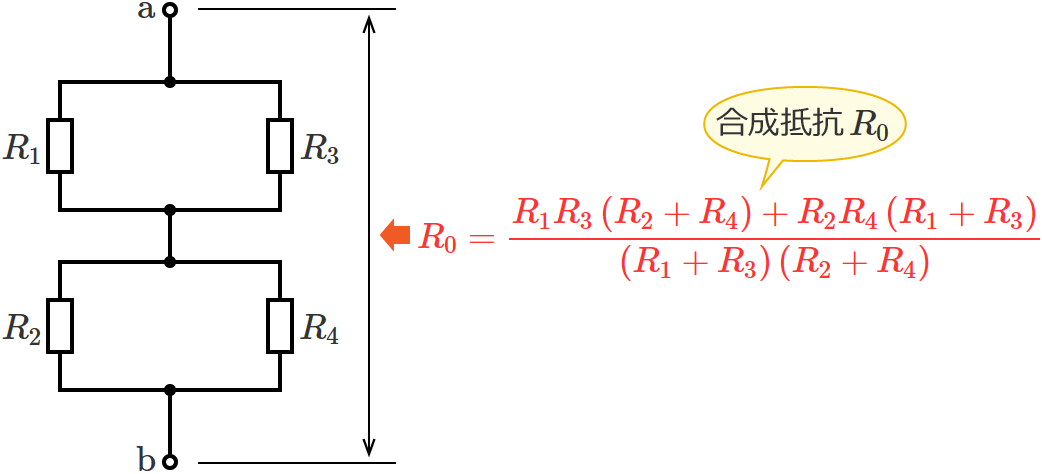
STEP3で求めた開放電圧 $V_0$ とSTEP4で求めた合成抵抗 $R_0$ は、
$V_0=\dfrac{R_2R_3-R_1R_4}{\left( R_1+R_3\right) \left( R_2+R_4\right)} V$
$R_0=\dfrac{R_1R_3\left( R_2+R_4\right) +R_2R_4\left( R_1+R_3\right)}{\left(R_1+R_3\right)\left(R_2+R_4\right)}$
で、端子 $\mathrm{a}$-$\mathrm{b}$ 間の抵抗は $R_5$ なので、これらをテブナンの定理の式(①式)に代入すると、
$I=\dfrac{V_0}{R_0+R_5}$
$=\dfrac{\dfrac{R_2R_3-R_1R_4}{\left( R_1+R_3\right) \left( R_2+R_4\right)} V}{\dfrac{R_1R_3\left( R_2+R_4\right) +R_2R_4\left( R_1+R_3\right)}{\left( R_1+R_3\right) \left(R_2+R_4\right)} +R_5}$
$=\dfrac{R_2R_3-R_1R_4}{R_1R_3\left( R_2+R_4\right) +R_2R_4\left( R_1+R_3\right) +R_5\left( R_1+R_3\right) \left( R_2+R_4\right)} V$
$\therefore I=\dfrac{R_2R_3-R_1R_4}{R_1R_3\left( R_2+R_4\right) +R_2R_4\left( R_1+R_3\right) +R_5\left( R_1+R_3\right) \left( R_2+R_4\right)} V$ (抵抗 $R_5$ に流れる電流 $I$ )
となり、この電流 $I$ が抵抗 $R_5$ に流れる電流になります。
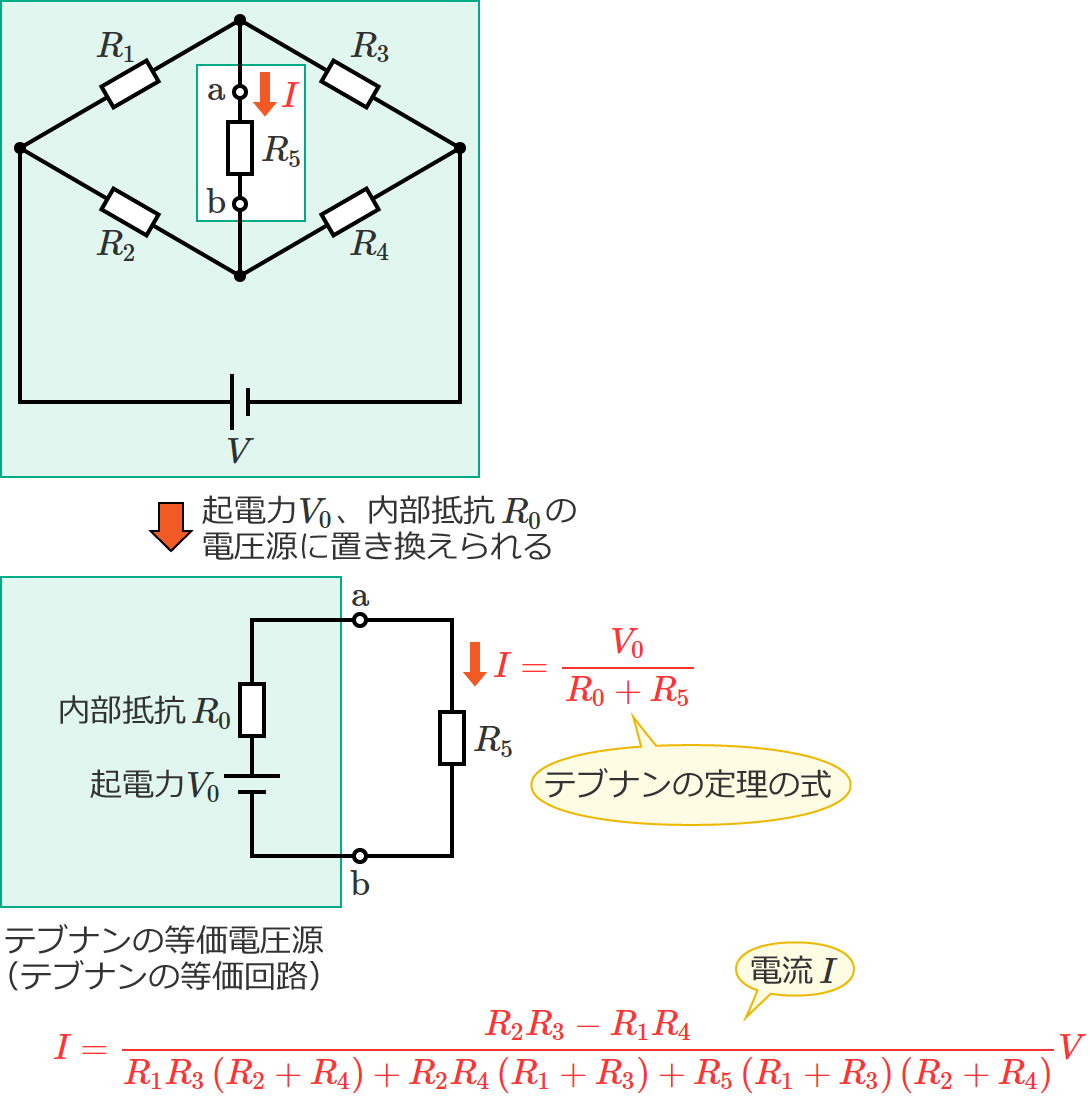
以上で、ブリッジ回路の抵抗 $R_5$ に流れる電流 $I$ が求められました。
続いて、テブナンの定理を証明してみます。
テブナンの定理の証明
重ね合わせの理を用いて、テブナンの定理の証明をしてみます。
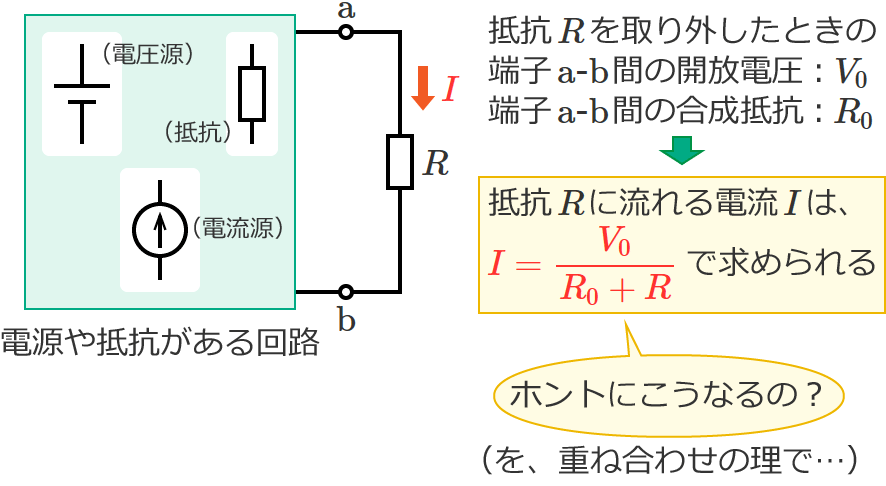
次の図2のような電源を含む回路があるとして、この回路の抵抗 $R$ を取り外したときの端子 $\mathrm{a}$-$\mathrm{b}$ 間の開放電圧は $V_0$ 、端子 $\mathrm{a}$-$\mathrm{b}$ 間の合成抵抗は $R_0$ であるものとします。
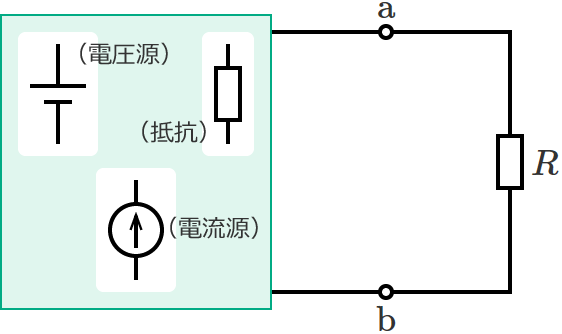
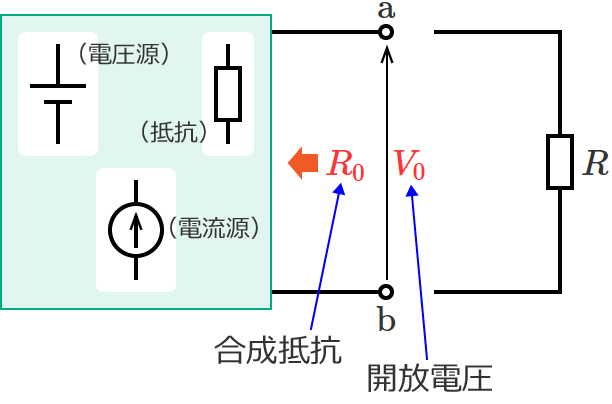
端子 $\mathrm{a}$-$\mathrm{b}$ 間の合成抵抗 $R_0$ は、抵抗 $R$ を取り外して、電圧源を短絡し、電流源を開放したときの合成抵抗です。
この回路の端子 $\mathrm{a}$-$\mathrm{b}$ 間に、電圧 $V_0$ の電圧源(端子 $\mathrm{a}$-$\mathrm{b}$ 間の開放電圧と同じ電圧の電圧源)を2つ互いに逆向きになるように追加(接続)します。
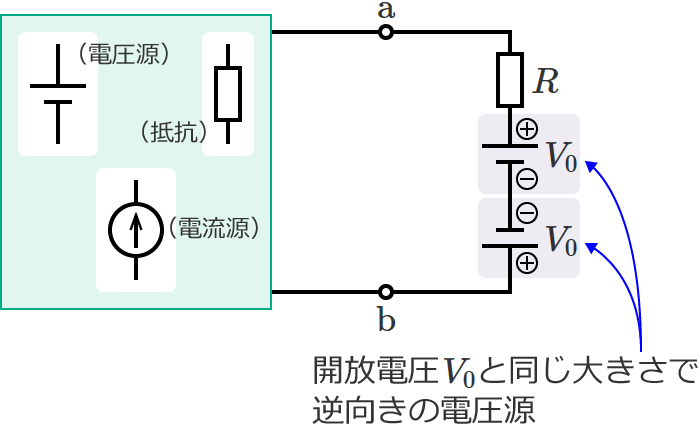
追加した2つの電圧源は電圧の大きさが同じで互いに逆向きなので、2つの電圧源による電圧は打ち消されます。そのため、この追加した2つの電圧源は、回路の電圧や電流に影響を与えません。
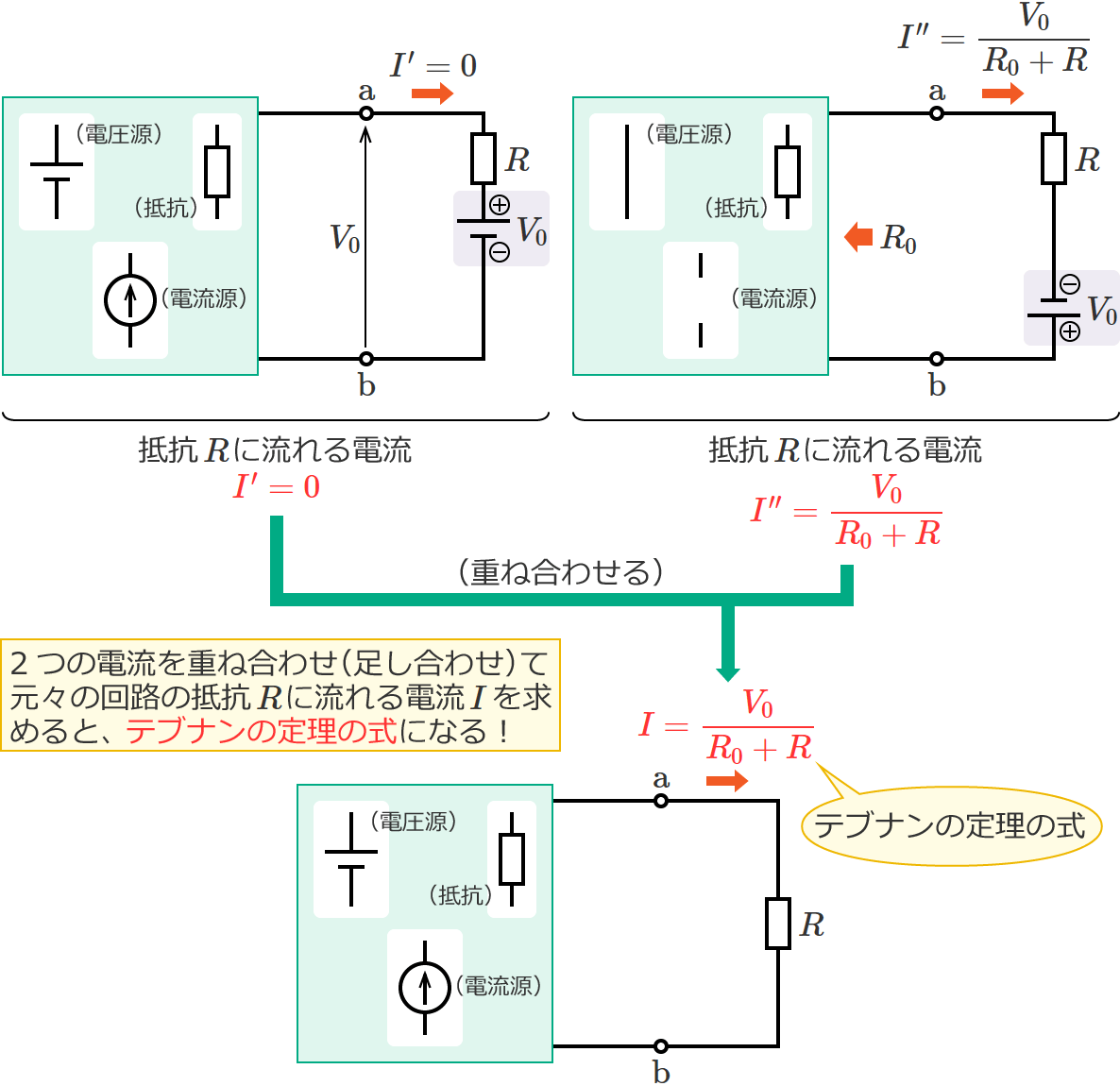
抵抗 $R$ に流れる電流 $I$ を重ね合わせの理により求めるため、図3の回路から次の2つの回路(図4と図5)をつくります。図4は追加した下側の電圧源だけを取り除いた回路で、図5は追加した下側の電圧源だけを残して他の電源を取り除いた回路です。
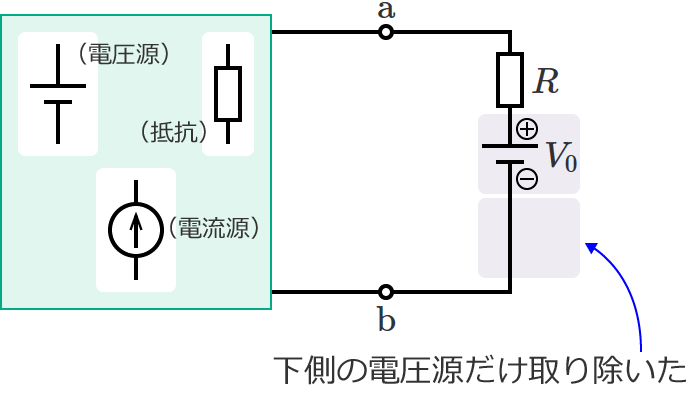
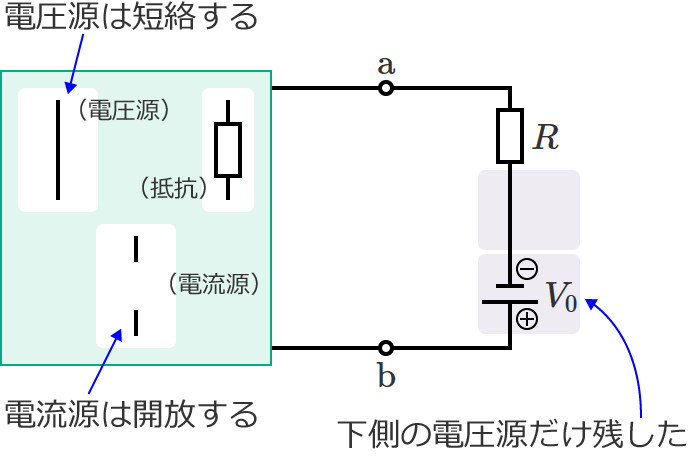
重ね合わせの理の場合も、電源を取り除くときはテブナンの定理と同じように、電圧源は短絡し、電流源は開放します。
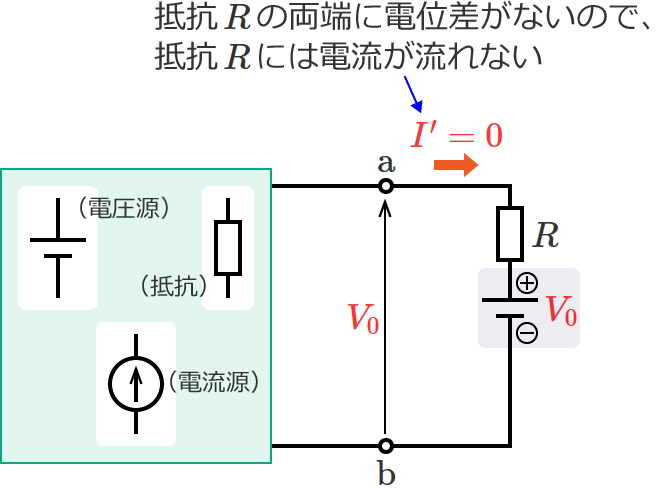
図4の回路では、端子 $\mathrm{a}$-$\mathrm{b}$ 間の開放電圧 $V_0$ と同じ大きさで逆向きの電圧源が接続されているので、抵抗 $R$ には電流が流れません。したがって、図4の回路の抵抗 $R$ に流れる電流 $I^\prime$[$\mathrm{A}$] は、
$\therefore I^\prime =0$ …⑥
となります。
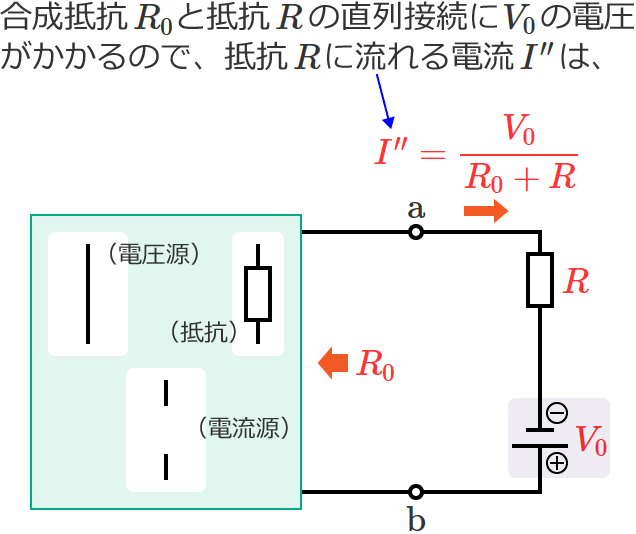
また、図5の回路では、抵抗 $R$ を取り外したときの端子 $\mathrm{a}$-$\mathrm{b}$ 間の合成抵抗が $R_0$ なので、図5の回路の抵抗 $R$ に流れる電流 $I^{\prime\prime}$[$\mathrm{A}$] は、
$\therefore I^{\prime\prime} =\dfrac{V_0}{R_0+R}$ …⑦
となります。
以上で求めた⑥と⑦の電流を重ね合わせると抵抗 $R$ に流れる電流 $I$ になるので、⑥と⑦を足し合わせて電流 $I$ を求めると、
$I=I^\prime +I^{\prime\prime} =0+\dfrac{V_0}{R_0+R}$
$\therefore I=\dfrac{V_0}{R_0+R}$ (電流 $I$ )
となり、重ね合わせの理により求めた電流 $I$ は、テブナンの定理の式と同じ式になります。(証明終わり)
ちなみに、抵抗 $R$ に流れる電流が $I=\dfrac{V_0}{R_0+R}$ で表わせられるということは、端子 $\mathrm{a}$-$\mathrm{b}$ より左側の回路は、次のように「内部抵抗がある1つの電圧源」(テブナンの等価電圧源)で等価的に置き換えることができるということも示しています。
テブナンの定理はおぼえておくとなにかと役に立つ定理ですので、テブナンの定理の使い方はおぼえておくようにしましょう!
- テブナンの定理は、電源を含む回路において、ある特定の素子に流れる電流を求めたいときに有用な定理
- 開放電圧 $V_0$ と開放した端子間の合成抵抗 $R_0$(電圧源は短絡し、電流源は開放する)が分かれば、$I=\dfrac{V_0}{R_0+R}$ で抵抗 $R$ に流れる電流 $I$ を求められる

スポンサーリンク
スポンサーリンク
このページでは直流回路でテブナンの定理を解説しましたが、テブナンの定理は交流回路でも成り立ちます。交流回路でのテブナンの定理の解説については、こちらの交流回路のテブナンの定理のページを参考にしてみてください。
また、テブナンの定理は回路を「電圧源」に置き換える定理ですが、電圧源ではなく「電流源」に置き換える定理をノートンの定理といいます。ノートンの定理については、こちらのノートンの定理のページを参考にしてみてください。
スポンサーリンク
テブナンの定理 関連ページ
- 合成抵抗の求め方(計算方法)
- 合成抵抗の計算は直流回路、交流回路の計算をするときの基本になります。合成抵抗の計算は複雑そうに思えますが、基本的には、抵抗が2個の場合の直列接続または並列接続の合成抵抗の求め方さえ分かっていれば、ほとんどの回路の合成抵抗を求めることができます。
- 短絡されている抵抗がある場合の合成抵抗の求め方
- 短絡されている抵抗がある場合の合成抵抗の求め方について解説しています。回路に短絡されている抵抗があるんだけど、どうやって合成抵抗を求めるの?なんてときに参考にしてみてください。
- 重ね合わせの理
- 重ね合わせの理について解説しています。重ね合わせの理は、重ね合わせの定理、重ねの理とも呼ばれ、回路に電源が複数ある場合によく使われる定理です。電圧源が2つある回路や、電圧源と電流源が混在した回路などの重ね合わせの理を使った計算方法についても解説していますので参考にしてみてください。
- ノートンの定理
- ノートンの定理について解説しています。ノートンの定理は等価電流源の定理とも呼ばれ、回路の特定の素子にかかる電圧を求めるときに有用な定理です。ノートンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。
- ミルマンの定理
- ミルマンの定理について解説しています。ミルマンの定理は全電圧の定理とも呼ばれ、抵抗と電源の直列接続が複数並列に接続されている回路の端子電圧を求めたいときに有用な定理です。ミルマンの定理の式の導出方法や、ミルマンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。
- 分圧の法則による直流回路の計算
- 分圧の法則を使った直流回路の計算方法の例です。分圧の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。
- 分流の法則による直流回路の計算
- 分流の法則を使った直流回路の計算方法の例です。分流の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。
- ループ解析(基本)
- 直流回路の計算をするときによく使われる「ループ解析」の方法と基本的な手順について解説しています。ループ解析はキルヒホッフの第二法則(電圧則)を応用した電気回路の計算方法です。
- 電圧源と電流源の等価変換
- 電圧源と電流源の等価変換について解説しています。電圧源と電流源が等価になるための条件や、電圧源から電流源、電流源から電圧源への等価変換のやり方などについて解説していますので参考にしてみてください。
- 電源から供給できる最大電力(最大有能電力)
- 電源から供給できる最大電力(最大有能電力)について解説しています。内部抵抗をもつ電源は、負荷に供給できる電力に上限(限界)があります。電源からの供給電力が最大になるための条件や、負荷に供給できる電源の最大電力(最大有能電力)などについて解説していますので、参考にしてみてください。
- コンデンサの静電容量と電荷の計算の基本(直列接続と並列接続)
- コンデンサの静電容量と電荷の計算の基本についてまとめています。コンデンサの計算は、コンデンサ2個を直列接続または並列接続したときの考え方と計算方法が基本になります。
- 合成静電容量の求め方(計算方法)
- 合成静電容量の計算は直流回路、交流回路の計算をするときの基本になります。合成静電容量の計算は複雑そうに思えますが、基本的には、コンデンサが2個の場合の直列接続または並列接続の合成静電容量の求め方さえ分かっていれば、ほとんどの回路の合成静電容量を求めることができます。
- ジュール熱とジュールの法則
- 抵抗や金属などの導体に電流が流れたときに発生するジュール熱と、ジュールの法則について解説しています。ジュール熱が発生する理由(原理)についても解説していますので、ジュール熱・ジュールの法則の勉強の参考にしてみてください。


