電気のお勉強｜直流回路｜合成抵抗の求め方（計算方法）

スポンサーリンク

合成抵抗の計算は直流回路、交流回路の計算をするときの基本になります。

 

合成抵抗の計算は、抵抗の数が多くなると複雑そうに思えてしまいますが、基本的には、抵抗が2個の場合の直列接続または並列接続の合成抵抗の求め方さえ分かっていれば、ほとんどの回路の合成抵抗を求めることができます。

 

回路が複雑になると計算は多少大変になることもありますが、求め方（考え方）はけっこう単純だったりします。

 

それでは、合成抵抗を求めるときの基本になる「合成抵抗の公式」からいってみましょう！

 

スポンサーリンク

 

合成抵抗の計算をするためには、まず初めに合成抵抗の公式をおぼえておかなければなりません。

 

合成抵抗の公式には、抵抗が直列接続のときの合成抵抗を求める公式と、抵抗が並列接続のときの合成抵抗を求める公式があります。

 

抵抗が直列接続のときの合成抵抗の公式

次の図のように、抵抗が $n$ 個直列接続されている回路があるとします。

 

 

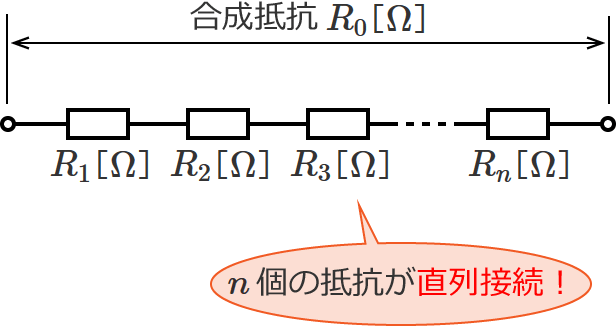
この回路の合成抵抗 $R_0$［$ \mathrm{\Omega} $］を求める公式は、次のようになります。

 

 

直列接続の場合は、並んでいる抵抗をただ足していくだけです。

 

また、この式をみると分かるように、直列接続の場合は抵抗の値が大きくなればなるほど、抵抗の数が増えれば増えるほど合成抵抗の大きさも大きくなります。

 

直列接続の合成抵抗は、ただ足すだけなので簡単ですね！

 

抵抗が並列接続のときの合成抵抗の公式

次は並列接続です。

 

次の図のように、抵抗が $n$ 個並列接続されている回路があるとします。

 

 

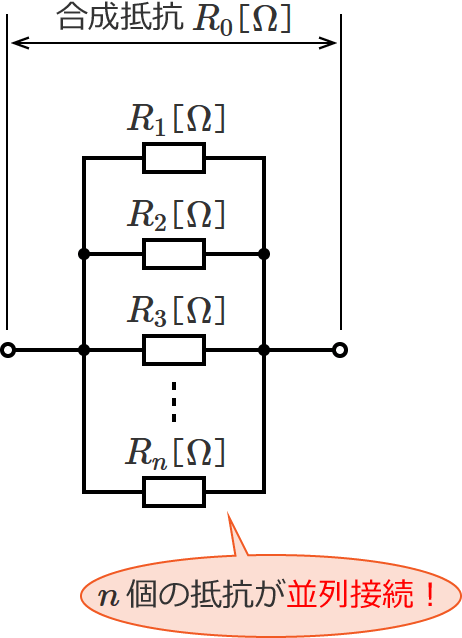
この回路の合成抵抗 $R_0$［$ \mathrm{\Omega} $］を求める公式は、次のようになります。

 

 

この式も先ほどの直列接続の公式と同じように、ただ足しているように見えますが、何か違いますよね？

 

抵抗の値をひっくり返したもの（逆数）を足しています。

 

この抵抗の逆数はコンダクタンスといって、電流の流れやすさを表わすものです。

 

つまり、コンダクタンス（抵抗の逆数）が大きいと電流が流れやすく、コンダクタンスが小さいと電流が流れにくい、ということになります。

 

ちょっと思い出してみると、抵抗は電流の流れにくさを表わすものでしたよね？

 

その抵抗の逆数をとっているので、意味が反対のものになっているということですね。

 

 

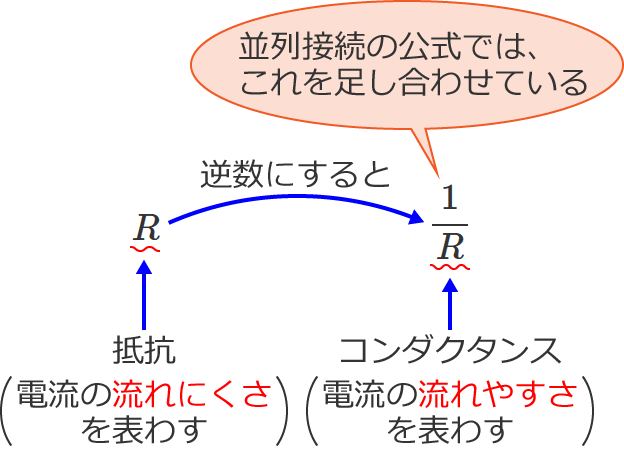
このように、並列接続のときは抵抗の逆数（コンダクタンス）を足して合成抵抗を求めます。

 

ここでちょっと注意ですが、並列接続された抵抗の合成抵抗を求めるときに和分の積がよく使われます。和分の積は、並列接続された抵抗が2つのときに使える公式で、抵抗が3つ以上のときは使えません。つまり、

 

 

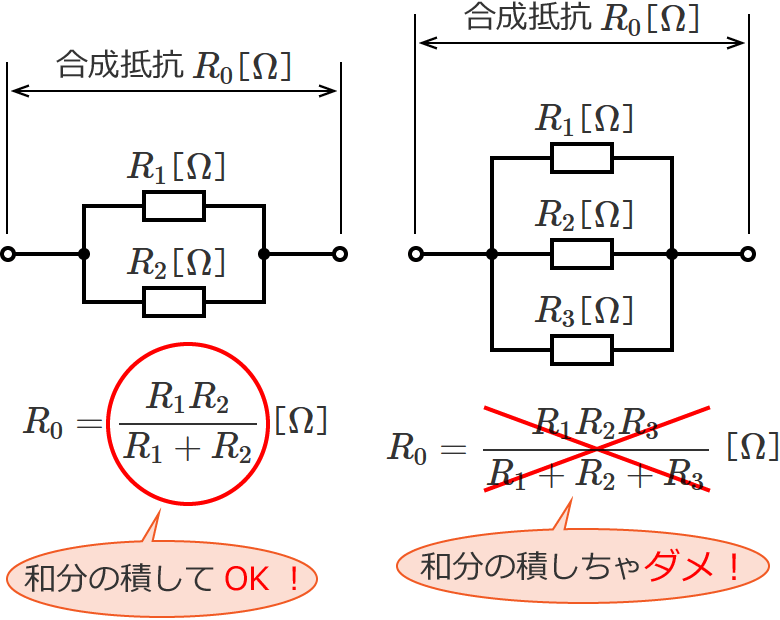
ということになります。間違っておぼえてしまっている人が多いので注意しましょう！

 

ちなみに、和分の積は、

 

並列接続の合成抵抗の公式： $\dfrac{1}{R_0} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} + \cdots + \dfrac{1}{R_n}$

 

を、抵抗2個だけで考えたときの式そのまんまなんです。抵抗2個だけだと、

 

$\dfrac{1}{R_0} = \dfrac{1}{R_1} + \dfrac{1}{R_2}$　、　$\dfrac{1}{R_0} = \dfrac{R_1 + R_2}{R_1 \times R_2}$

 

分母と分子をひっくり返して、　$\therefore R_0 = \dfrac{R_1 \times R_2}{R_1 + R_2}$

 

ねっ？　和分の積になっていますよね。

 

それから、もう一つ気を付けてほしいのは、並列接続の公式を使うときに右辺だけを計算して合成抵抗だ！としないようにしましょう。

 

 

公式の左辺も逆数になっているので、右辺を計算した後にひっくり返さなければなりません。

 

 

つまり、並列接続の合成抵抗の公式を $R_0 = \cdots$ で書くならば、

 

 

となります。

 

ここまでで、直列接続と並列接続の合成抵抗を求める公式が分かったと思うので、次は公式を使って色々な回路の合成抵抗を計算してみます？

 

 

まずは抵抗1個の場合です。

 

って、1個だと合成しようがないですね…

 

ま〜、とりあえず。

 

抵抗1個直列接続の場合

抵抗が1個だけなので、回路は次のようになります。

 

 

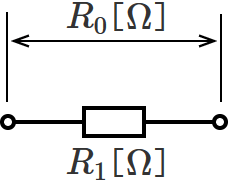
直列接続の合成抵抗の公式にあてはめてみます。

 

 

で、でました！

 

抵抗1個並列接続の場合

抵抗が1個だけなので、回路は次のようになります。

 

 

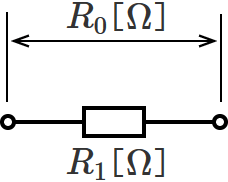
並列接続の合成抵抗の公式にあてはめてみます。

 

$\dfrac{1}{R_0} = \dfrac{1}{R_1}$

 

両辺の分母と分子をひっくり返します。

 

 

で、で、でちゃいました！

 

抵抗1個の場合は、直列接続も並列接続も同じになります。というより、抵抗1個の場合を直列接続とか並列接続って言うのも変なんですけどね。（ふつうは言いません。）
元の回路が同じなので、当然、求めたものも同じになります。

抵抗が2個の場合です。

 

抵抗が2個の場合が合成抵抗を求めるときの一番の基礎になるので、ここでつまずかないようにしましょう。

 

これさえおぼえておけば、ほとんどの合成抵抗の問題は解けます。

 

抵抗2個直列接続の場合

抵抗2個が直列接続なので、次のような回路になります。

 

 

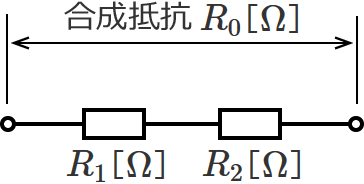
直列接続の合成抵抗の公式にあてはめてみます。

 

 

公式からそのままで導かれましたね。

 

直列接続は簡単です。

 

抵抗2個並列接続の場合

抵抗2個が並列接続なので、次のような回路になります。

 

 

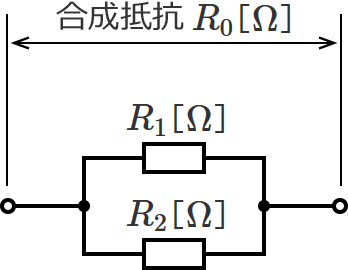
並列接続の合成抵抗の公式にあてはめてみます。抵抗の逆数を足していけばよかったですね。

 

$\dfrac{1}{R_0} = \dfrac{1}{R_1} + \dfrac{1}{R_2}$

 

あとはこれを計算して、$R_0 = \cdots$ という式にします。

 

$\dfrac{1}{R_0} = \dfrac{R_1 + R_2}{R_1 \times R_2}$　、ひっくり返して、

 

 

ちゃんと和分の積になりました。

 

抵抗が3個の場合です。

 

このあたりから計算がちょっと大変になってきますが、計算がちょっと大変（めんどくさい）になるだけで、考え方はむずかしくないですよ。

 

抵抗3個直列接続の場合

抵抗3個が直列接続なので、次のような回路になります。

 

 

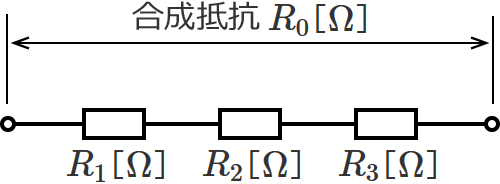
直列接続の合成抵抗の公式にあてはめてみます。

 

 

直列接続の場合は公式そのまんまなので、何個になっても簡単ですね。

 

抵抗3個並列接続の場合

抵抗3個が並列接続なので、次のような回路になります。

 

 

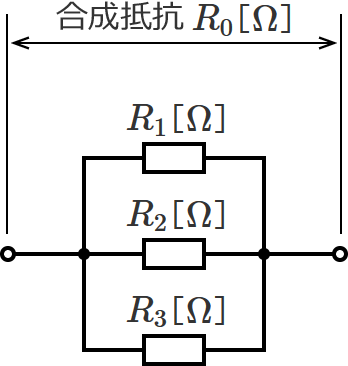
並列接続の合成抵抗の公式にあてはめてみます。

 

$\dfrac{1}{R_0} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3}$

 

あら、ちょっとめんどくさそう。計算します。

 

$\dfrac{1}{R_0} = \dfrac{R_2 R_3 + R_1 R_3 + R_1 R_2}{R_1 \times R_2 \times R_3}$　、ひっくり返して、

 

 

あ、そんなにめんどくさいことはありませんでした。

 

ここで①式を見てほしいのですが、並列接続の合成抵抗の公式のところで「抵抗が3つ以上並列接続されているときには和分の積は使えません。」と書きましたが、①式をみると、やっぱり和分の積にはなっていないですよね！

 

抵抗3個並列接続の場合の別解

抵抗3個が並列接続のときの回路は、和分の積だけを使って解くこともできます。

 

 

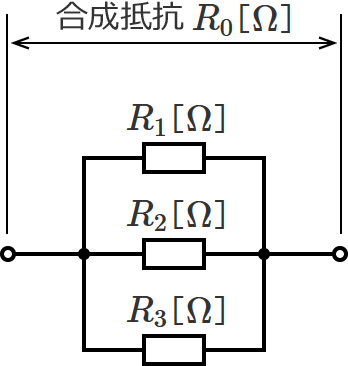
この回路をよ〜く見てみると、これは抵抗2個が並列に接続された回路に、さらに抵抗1個が並列に接続された回路に見えてきます。

 

 

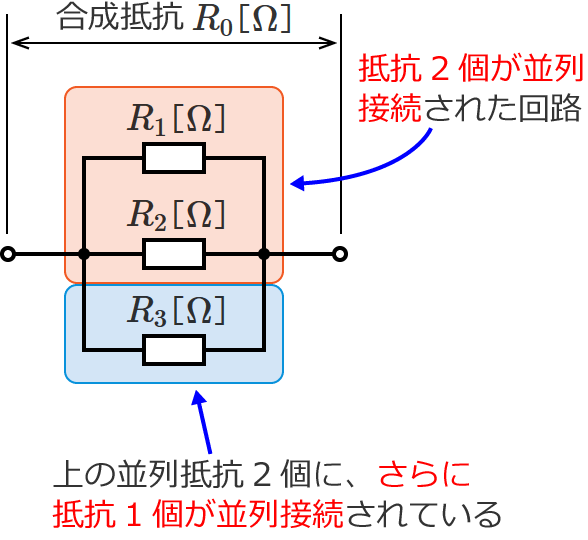
なので、$R_1$ と $R_2$ の抵抗を和分の積で合成してしまえば、2個の抵抗を1個の抵抗にすることができますね。

 

 

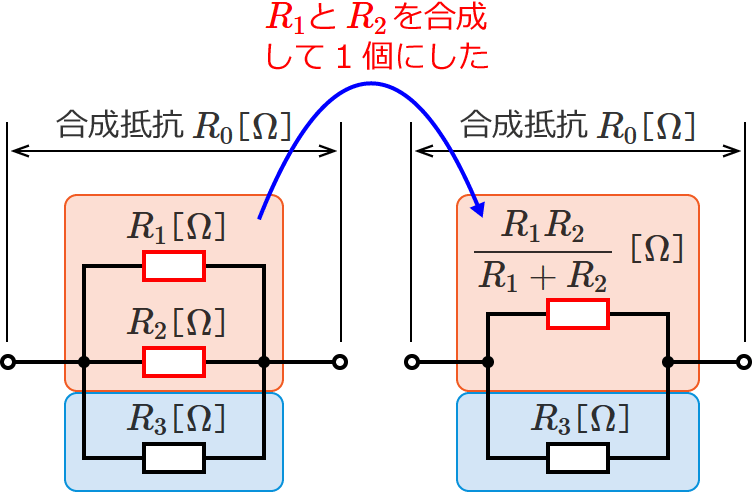
あとは抵抗2個の並列接続なので、これも和分の積して合成します。

 

$R_0 = \dfrac{\dfrac{R_1 R_2}{R_1 + R_2} \times R_3}{\dfrac{R_1 R_2}{R_1 + R_2} + R_3}$ $= \dfrac{\dfrac{R_1 R_2 R_3}{R_1 + R_2}}{\dfrac{R_1 R_2 + R_3 \left( R_1 + R_2 \right)}{R_1 + R_2}}$ $= \dfrac{R_1 R_2 R_3}{R_1 R_2 + R_3 R_1 + R_3 R_2}$

 

 

 

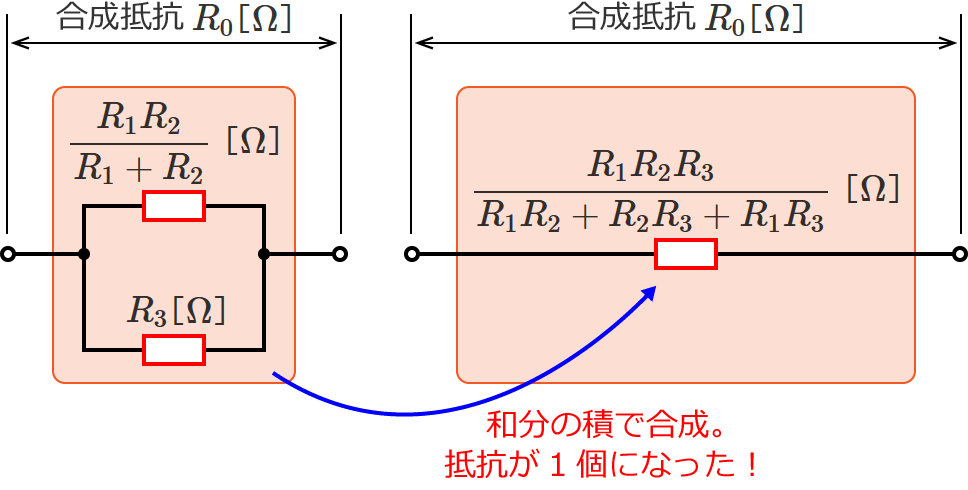
①と②は同じ結果になりました。

 

このように、和分の積だけを使っても合成抵抗を求めることができます。

 

抵抗2個並列接続とそれに直列接続1個の場合

抵抗2個が並列接続で、その並列接続された抵抗に、さらに直列に抵抗を1個接続するので回路は次のようになります。

 

 

この回路の場合、ここまでで計算してきたように公式にそのままあてはめることはできませんね。

 

合成抵抗を求めるときの考え方の基本は、とにかく回路を簡単にしていくことです。（回路を簡単にしていくという意味は、抵抗の数を減らしていくということです。）

 

では、この回路をどうやって簡単にしていけばいいでしょうか？

 

上の回路図をじ〜っと見てみましょう。

 

すると、おやっ？　っと、たぶん気付きます。

 

回路の左側は抵抗2個の並列接続になっていますよね？

 

 

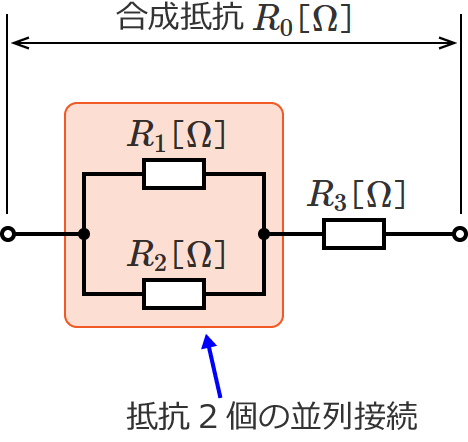
ということは、この2個並列接続された抵抗を合成してしまえば、2個の抵抗を1個の抵抗にすることができます。

 

$R_1$ と $R_2$ の2個の抵抗の並列接続なので和分の積で、えぃっ！と求めてしまいましょう。すると、次のようになります。

 

 

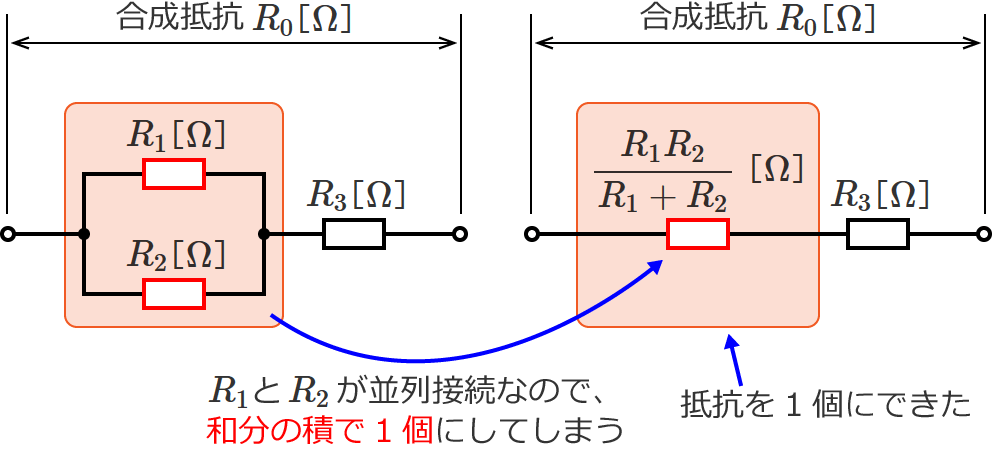
これで、並列接続されている2個の抵抗 $R_1$ と $R_2$ が1個になって、2個直列接続の回路になりました。

 

あとは抵抗2個の直列接続の回路なので、残りの抵抗2個を足せばいいですね。

 

$R_0 = \dfrac{R_1 R_2}{R_1 + R_2} + R_3$ $= \dfrac{R_1 R_2 + R_3 \left( R_1 + R_2 \right)}{R_1 + R_2}$ $= \dfrac{R_1 R_2 + R_3 R_1 + R_3 R_2}{R_1 + R_2}$

 

 

 

これで合成抵抗が求められました。

 

 

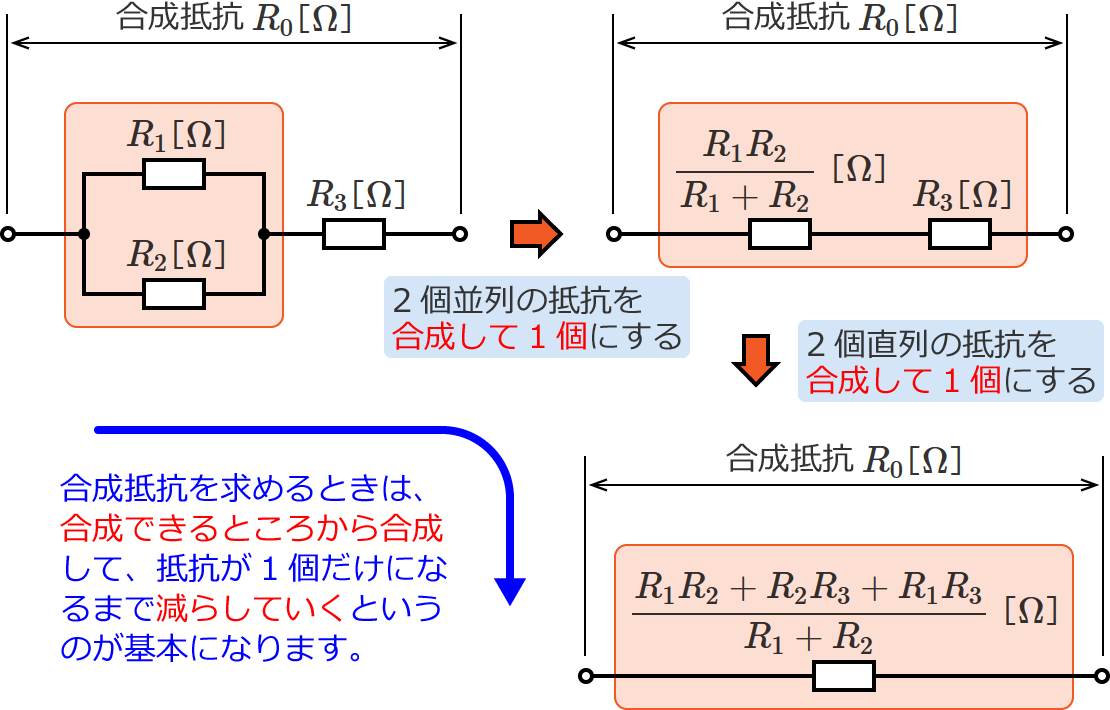
合成抵抗を求めるときは、とにかく回路を簡単にしていくというのが基本で、並列2個を1個に、直列は1個にまとめて・・・という繰り返しで求めていきます。

 

 

抵抗が短絡されている場合の合成抵抗の求め方については、こちらの短絡されている抵抗がある場合の合成抵抗の求め方のページを参考にしてみてください。

 

合成抵抗を求めるときと合成静電容量を求めるときでは求め方（和分の積か？足すだけか？）が直列接続と並列接続で逆になります。合成静電容量の求め方については、合成静電容量の求め方（計算方法）のページを参考にしてみてください。

 

回路の直列接続と並列接続については、こちらの直列接続と並列接続のページを参考にしてみてください。

電気のお勉強のＴＯＰ　←BACK

NEXT→　短絡されている抵抗がある場合の合成抵抗の求め方

スポンサーリンク

合成抵抗の求め方（計算方法）　関連ページ

短絡されている抵抗がある場合の合成抵抗の求め方

短絡されている抵抗がある場合の合成抵抗の求め方について解説しています。回路に短絡されている抵抗があるんだけど、どうやって合成抵抗を求めるの？なんてときに参考にしてみてください。

重ね合わせの理

重ね合わせの理について解説しています。重ね合わせの理は、重ね合わせの定理、重ねの理とも呼ばれ、回路に電源が複数ある場合によく使われる定理です。電圧源が2つある回路や、電圧源と電流源が混在した回路などの重ね合わせの理を使った計算方法についても解説していますので参考にしてみてください。

テブナンの定理

テブナンの定理（鳳-テブナンの定理）について解説しています。テブナンの定理は等価電圧源の定理とも呼ばれ、回路の特定の素子に流れる電流を求めるときに有用な定理です。テブナンの定理を使った回路の計算方法や、テブナンの定理の証明についても解説していますので参考にしてみてください。

ノートンの定理

ノートンの定理について解説しています。ノートンの定理は等価電流源の定理とも呼ばれ、回路の特定の素子にかかる電圧を求めるときに有用な定理です。ノートンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。

ミルマンの定理

ミルマンの定理について解説しています。ミルマンの定理は全電圧の定理とも呼ばれ、抵抗と電源の直列接続が複数並列に接続されている回路の端子電圧を求めたいときに有用な定理です。ミルマンの定理の式の導出方法や、ミルマンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。

分圧の法則による直流回路の計算

分圧の法則を使った直流回路の計算方法の例です。分圧の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。

分流の法則による直流回路の計算

分流の法則を使った直流回路の計算方法の例です。分流の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。

ループ解析（基本）

直流回路の計算をするときによく使われる「ループ解析」の方法と基本的な手順について解説しています。ループ解析はキルヒホッフの第二法則（電圧則）を応用した電気回路の計算方法です。

電圧源と電流源の等価変換

電圧源と電流源の等価変換について解説しています。電圧源と電流源が等価になるための条件や、電圧源から電流源、電流源から電圧源への等価変換のやり方などについて解説していますので参考にしてみてください。

電源から供給できる最大電力（最大有能電力）

電源から供給できる最大電力（最大有能電力）について解説しています。内部抵抗をもつ電源は、負荷に供給できる電力に上限（限界）があります。電源からの供給電力が最大になるための条件や、負荷に供給できる電源の最大電力（最大有能電力）などについて解説していますので、参考にしてみてください。

コンデンサの静電容量と電荷の計算の基本（直列接続と並列接続）

コンデンサの静電容量と電荷の計算の基本についてまとめています。コンデンサの計算は、コンデンサ2個を直列接続または並列接続したときの考え方と計算方法が基本になります。

合成静電容量の求め方（計算方法）

合成静電容量の計算は直流回路、交流回路の計算をするときの基本になります。合成静電容量の計算は複雑そうに思えますが、基本的には、コンデンサが2個の場合の直列接続または並列接続の合成静電容量の求め方さえ分かっていれば、ほとんどの回路の合成静電容量を求めることができます。

ジュール熱とジュールの法則

抵抗や金属などの導体に電流が流れたときに発生するジュール熱と、ジュールの法則について解説しています。ジュール熱が発生する理由（原理）についても解説していますので、ジュール熱・ジュールの法則の勉強の参考にしてみてください。