ジュール熱とジュールの法則

※ページ内にPR･広告が含まれる場合があります。

次のように、抵抗に電池を接続してみます。

抵抗に電池をつないだ電気回路

すると、抵抗に電圧がかかるので、抵抗には電流が流れます。

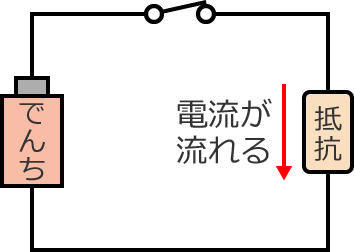
抵抗に電流が流れる

そして、この抵抗を触ってみると…

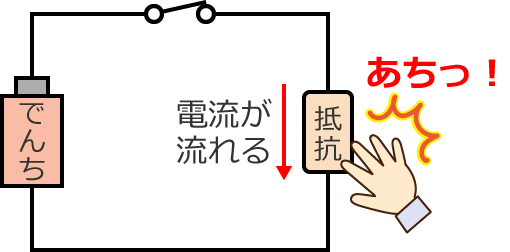
抵抗を触ると熱い

となります。

この「あちっ！」っとなるのは、

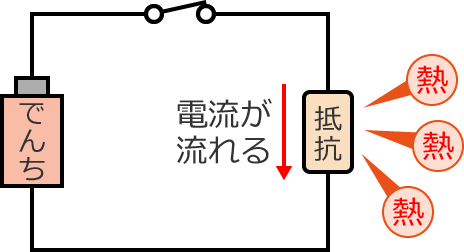
抵抗に電流が流れると、抵抗から熱が発生する

からなんです。（抵抗を触ってみたら熱かった！なんて経験したことないでしょうか？）

抵抗から熱が発生する

電流が流れることによって熱が発生するのは抵抗だけではなく、金属（例えば、電線）などでも熱が発生します。（電線にも抵抗はあるので、電線も抵抗といえば抵抗ですが…。）

細い電線に大きな電流を流してみると…

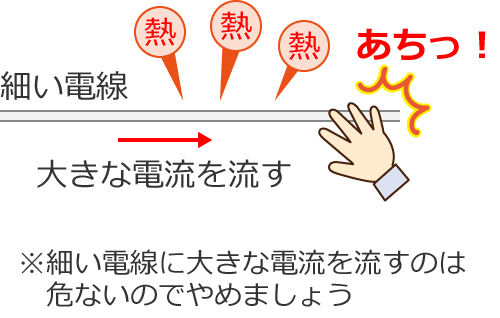
細い電線に大きな電流を流すと熱い

となります。

このように、抵抗や金属などの導体に電流が流れると、導体から熱が発生します。

この導体から発生する熱をジュール熱といいます。

ジュール熱

電気をよく通すものを導体、ほとんど通さないものを絶縁体（または不導体）といいます。導体と絶縁体については、こちらの導体と絶縁体（不導体）のページを参考にしてみてください。

ジュール熱はなぜ発生するのか？

ジュール熱はなぜ発生するのでしょうか？

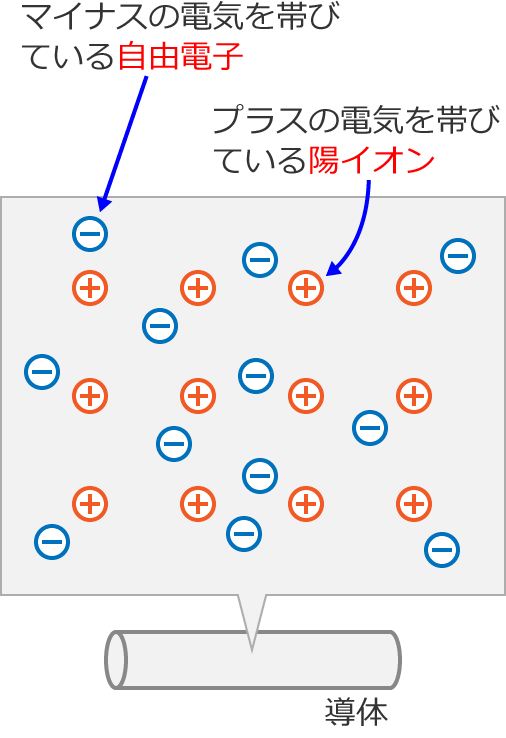
例えば、次のようなある導体があるとします。

導体の中には、プラスの電荷をもつ陽イオンと、自由に動き回ることができるマイナスの電荷をもつ自由電子が存在しています。

陽イオンと自由電子

この導体に電池をつなぐと導体には電場ができるので、マイナスの電荷をもつ自由電子は電場から力を受けて、電池のプラス側の方向に向かって加速（移動）します。

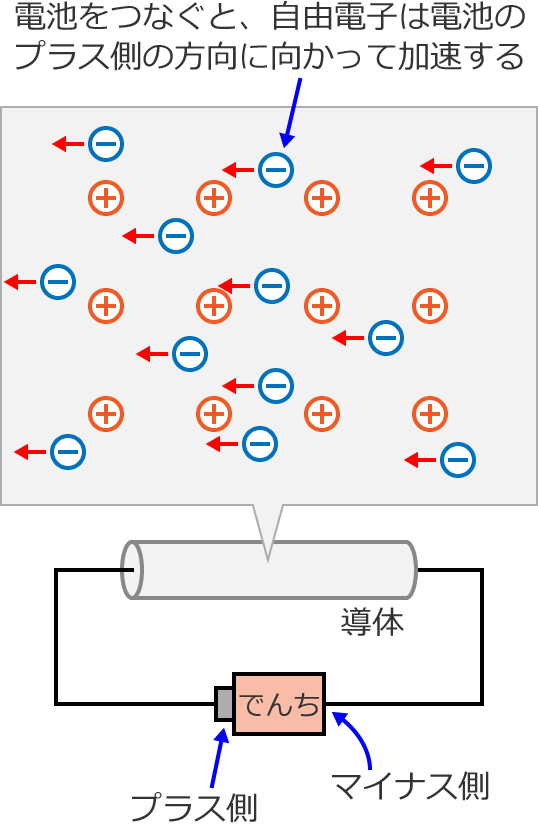
自由電子は電池のプラス側に移動する

電荷に力を及ぼす空間を電場（または電界）といいます。

このとき、導体中には陽イオンがあるので、電池のプラス側に向かって移動している自由電子は、

陽イオンに衝突 …
電池のプラス側に向かって加速…
陽イオンに衝突 …
電池のプラス側に向かって加速…

と、衝突と加速を繰り返しながら移動していきます。

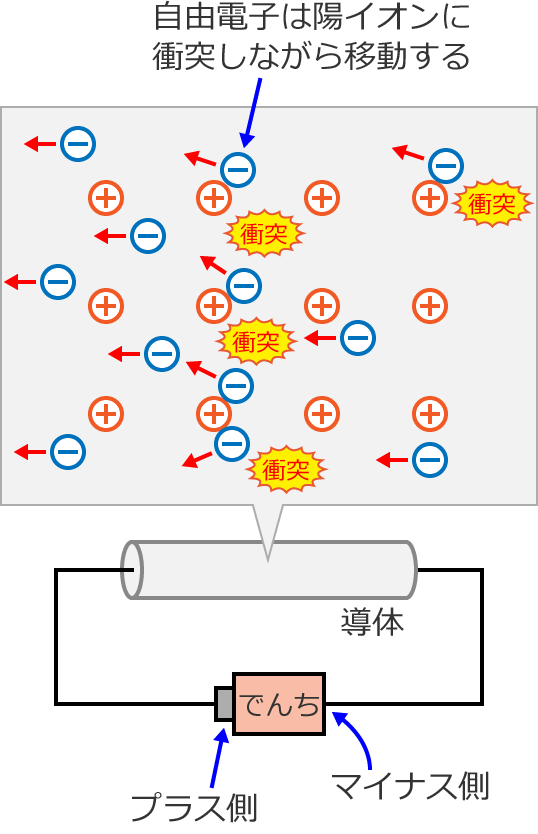
陽イオンに衝突しながら移動する

すると、自由電子と衝突した陽イオンの熱運動が激しくなるので、導体の温度が上昇し、導体から熱が発生します。

この熱がジュール熱です。

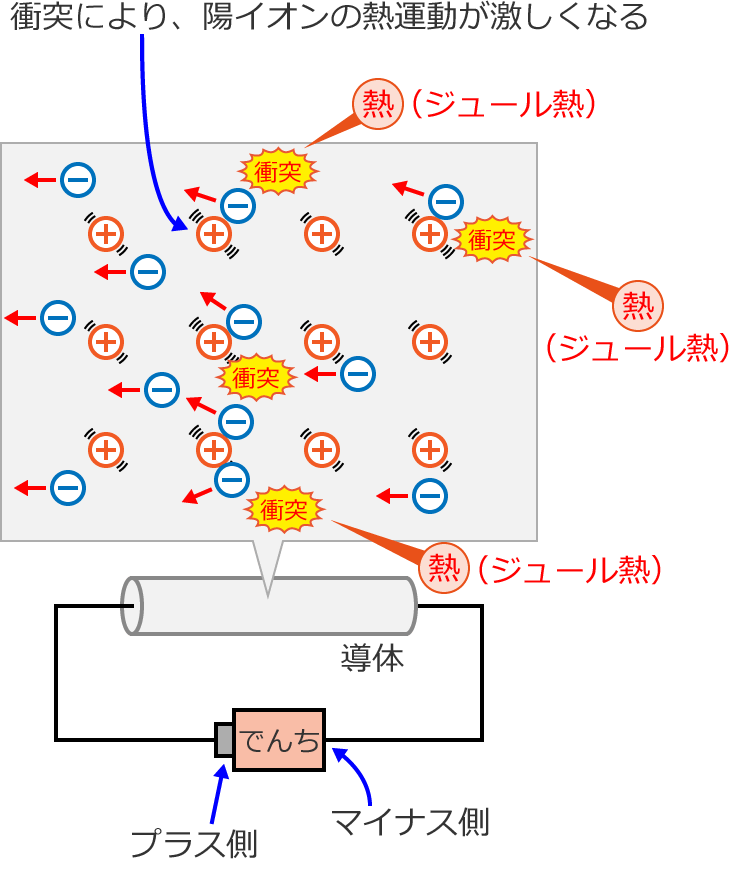
ジュール熱の発生原理

つまり、ジュール熱は、電場から力を受けて加速した自由電子が陽イオンと衝突し、陽イオンの熱運動が激しくなることによって発生するということです。

ジュールの法則

導体に流れる電流を $I$［$\mathrm{A}$］、導体の抵抗を $R$［$\Omega$］、導体に電流が流れる時間を $t$［$\mathrm{s}$］とすると、

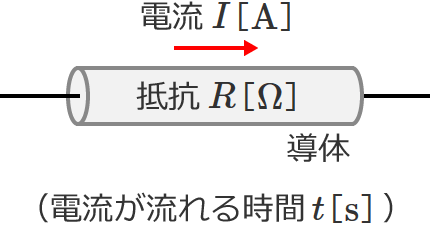
電流が流れる導体

導体から発生するジュール熱 $Q$［$\mathrm{J}$］は、

$Q=I^2Rt$　［$\mathrm{J}$］　…①

と表わされ、

ジュール熱は「電流の2乗」と「抵抗」の積に比例

します。これをジュールの法則といいます。

ジュール熱の単位は「$\mathrm{J}$」で、ジュールと読みます。

なお、ジュールの法則の式（①式）は、オームの法則を使うと、

$V=IR$（オームの法則）より、

$Q=I^2Rt=IR\cdot It=VIt$

$\therefore Q=VIt$　［$\mathrm{J}$］

$I=\dfrac{V}{R}$（オームの法則）より、

$Q=I^2Rt=\left(\dfrac{V}{R}\right)^2\cdot Rt=\dfrac{V^2}{R^2} Rt$ $=\dfrac{V^2}{R}t$

$\therefore Q=\dfrac{V^2}{R} t$　［$\mathrm{J}$］

とも表わすことができるので、

$Q=I^2Rt=VIt=\dfrac{V^2}{R} t$　［$\mathrm{J}$］　…②

となります。

②式よりジュール熱は、「電流と抵抗と時間」または「電圧と電流と時間」または「電圧と抵抗と時間」のいずれかが分かれば求められるので、ジュール熱の計算をするときは、場合に応じて②式の3つの式を使い分けましょう。

ジュール熱はこんなところで利用されています

通常、電気回路から熱が発生するのはよろしくありませんが（というか、できるだけ熱は発生させたくない）、

電気回路からは熱が発生する

モノによっては、電気エネルギーを熱エネルギーに変えてその熱を利用したい場合もあります。

例えば、電気ポットはお湯を沸かすのに熱が必要なので、その熱にジュール熱を利用しています。

電気ポット

電気ポットの他には、トースター、炊飯器、電気ストーブ、ドライヤーなどもジュール熱を利用しています。

トースターと炊飯器

電気ストーブとドライヤー

このようにジュール熱は、熱を必要とする家電製品など色々なところで利用されています。

ジュール熱とジュールの法則のまとめ

導体に電流が流れることによって発生する熱をジュール熱という
ジュール熱は「電流の2乗」と「抵抗」の積に比例する（ジュールの法則）
ジュールの法則（式）：$Q=I^2Rt=VIt=\dfrac{V^2}{R} t$　［$\mathrm{J}$］

電場（電界）中の電子が受ける力や運動については、こちらの電界中の電子の運動のページを参考にしてみてください。

合成静電容量の求め方（計算方法）　←BACK

NEXT→　電気のお勉強のＴＯＰ

ジュール熱とジュールの法則　関連ページ

合成抵抗の求め方（計算方法）: 合成抵抗の計算は直流回路、交流回路の計算をするときの基本になります。合成抵抗の計算は複雑そうに思えますが、基本的には、抵抗が2個の場合の直列接続または並列接続の合成抵抗の求め方さえ分かっていれば、ほとんどの回路の合成抵抗を求めることができます。
短絡されている抵抗がある場合の合成抵抗の求め方: 短絡されている抵抗がある場合の合成抵抗の求め方について解説しています。回路に短絡されている抵抗があるんだけど、どうやって合成抵抗を求めるの？なんてときに参考にしてみてください。
重ね合わせの理: 重ね合わせの理について解説しています。重ね合わせの理は、重ね合わせの定理、重ねの理とも呼ばれ、回路に電源が複数ある場合によく使われる定理です。電圧源が2つある回路や、電圧源と電流源が混在した回路などの重ね合わせの理を使った計算方法についても解説していますので参考にしてみてください。
テブナンの定理: テブナンの定理（鳳-テブナンの定理）について解説しています。テブナンの定理は等価電圧源の定理とも呼ばれ、回路の特定の素子に流れる電流を求めるときに有用な定理です。テブナンの定理を使った回路の計算方法や、テブナンの定理の証明についても解説していますので参考にしてみてください。
ノートンの定理: ノートンの定理について解説しています。ノートンの定理は等価電流源の定理とも呼ばれ、回路の特定の素子にかかる電圧を求めるときに有用な定理です。ノートンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。
ミルマンの定理: ミルマンの定理について解説しています。ミルマンの定理は全電圧の定理とも呼ばれ、抵抗と電源の直列接続が複数並列に接続されている回路の端子電圧を求めたいときに有用な定理です。ミルマンの定理の式の導出方法や、ミルマンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。
分圧の法則による直流回路の計算: 分圧の法則を使った直流回路の計算方法の例です。分圧の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。
分流の法則による直流回路の計算: 分流の法則を使った直流回路の計算方法の例です。分流の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。
ループ解析（基本）: 直流回路の計算をするときによく使われる「ループ解析」の方法と基本的な手順について解説しています。ループ解析はキルヒホッフの第二法則（電圧則）を応用した電気回路の計算方法です。
電圧源と電流源の等価変換: 電圧源と電流源の等価変換について解説しています。電圧源と電流源が等価になるための条件や、電圧源から電流源、電流源から電圧源への等価変換のやり方などについて解説していますので参考にしてみてください。
電源から供給できる最大電力（最大有能電力）: 電源から供給できる最大電力（最大有能電力）について解説しています。内部抵抗をもつ電源は、負荷に供給できる電力に上限（限界）があります。電源からの供給電力が最大になるための条件や、負荷に供給できる電源の最大電力（最大有能電力）などについて解説していますので、参考にしてみてください。
コンデンサの静電容量と電荷の計算の基本（直列接続と並列接続）: コンデンサの静電容量と電荷の計算の基本についてまとめています。コンデンサの計算は、コンデンサ2個を直列接続または並列接続したときの考え方と計算方法が基本になります。
合成静電容量の求め方（計算方法）: 合成静電容量の計算は直流回路、交流回路の計算をするときの基本になります。合成静電容量の計算は複雑そうに思えますが、基本的には、コンデンサが2個の場合の直列接続または並列接続の合成静電容量の求め方さえ分かっていれば、ほとんどの回路の合成静電容量を求めることができます。

電気のお勉強｜ジュール熱とジュールの法則