スポンサーリンク



短絡されている抵抗がある場合の合成抵抗の求め方

※ページ内にPR･広告が含まれる場合があります。

次のように、3つの抵抗（ $R_1$ 、$R_2$ 、$R_3$ ）でできている回路があるとして、

 

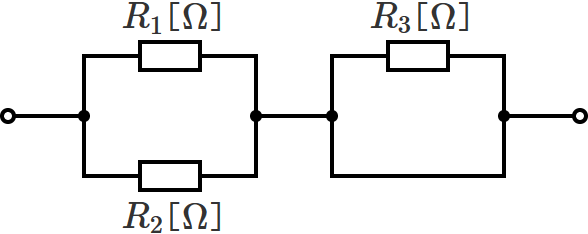
3つの抵抗でできている回路

 

この回路の合成抵抗を求めてみましょう。

 

合成抵抗を求めるときは、基本的に、

  • 2つ並列接続の抵抗は和分の積で1つにする
  • 直列接続の抵抗はただ足して1つにする

としていくと求められるのですが…

 

この回路をよく見ると、

 

抵抗 $R_3$ が短絡されてるし！

 

どうやって合成抵抗を求めるの？

 

みたいな回路になっています。（みたいなというか、そういう回路）

 

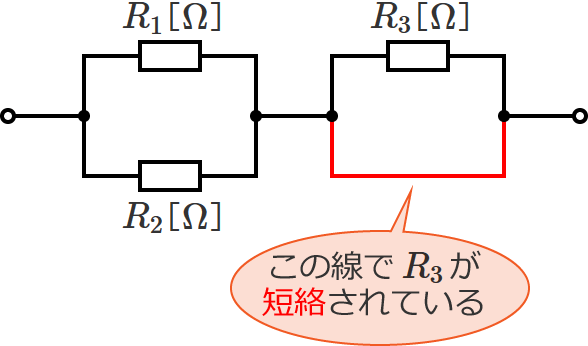
短絡されている抵抗がある回路

 

こんなときは、

 

短絡されている抵抗を無視する

 

または、

 

抵抗を短絡している線（電線）を $0\,\Omega$ の抵抗と考える

 

とすると、合成抵抗を求めることができます。

 

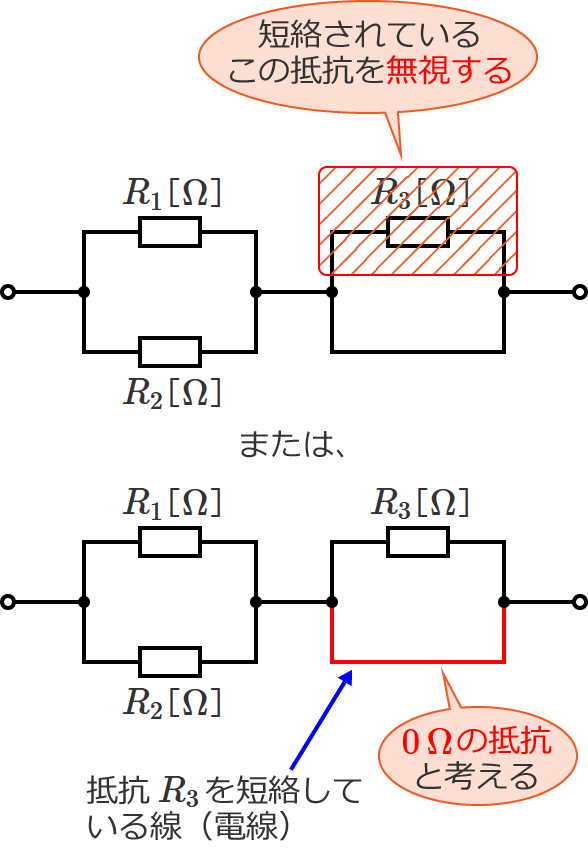
短絡されている抵抗がある場合の合成抵抗の求め方

 

このページでは、「短絡されている抵抗を無視する方法」と「抵抗を短絡している電線を $0\,\Omega$ の抵抗と考える方法」の2つの方法について解説していますので、短絡されている抵抗がある回路の合成抵抗を求めるときの参考にしてみてください。

 

スポンサーリンク

 

短絡されている抵抗を無視して合成抵抗を求める方法

次の回路の合成抵抗を、「短絡されている抵抗を無視する方法」で求めてみます。

 

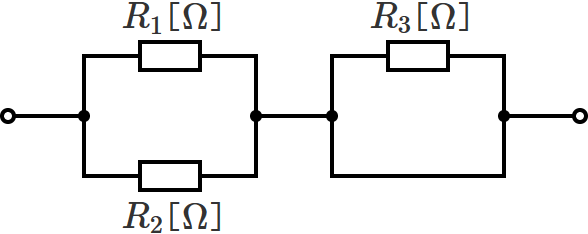
短絡されている抵抗がある回路

 

この回路の右側を見てみると、「抵抗 $R_3$ 」と「電線（線）」が並列に接続されているので、この回路は、電線で抵抗 $R_3$ が短絡されている回路になっています。

 

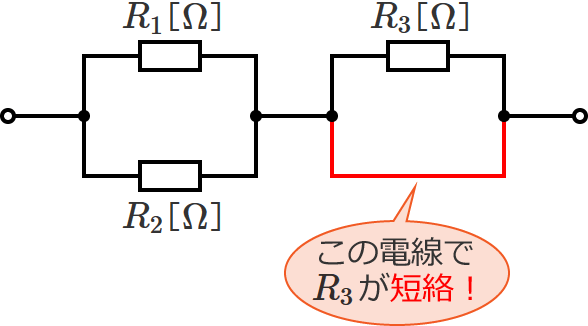
電線で抵抗R3が短絡されている

 

抵抗が短絡されているときは、短絡されている抵抗は無視して考えることができるので、

 

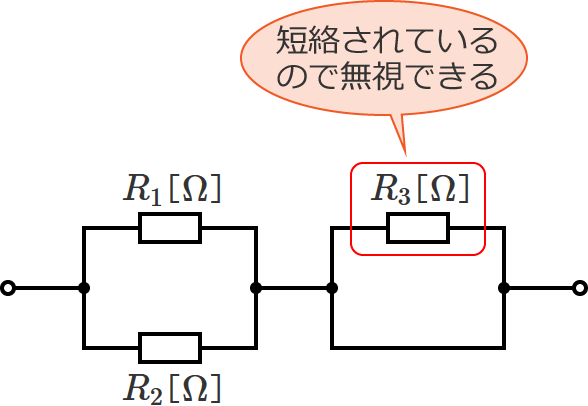
短絡されている抵抗は無視できる

 

抵抗 $R_3$ を取り除くと、回路は次のようになります。

 

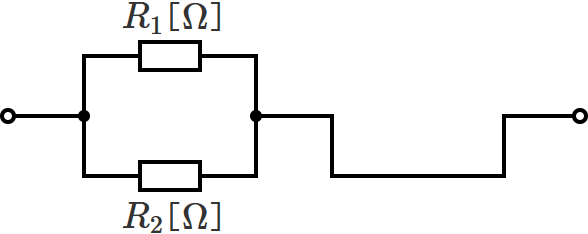
抵抗R3を取り除いた回路

 

すると、抵抗 $R_1$ と $R_2$ が並列接続されている回路になるので、あとは抵抗 $R_1$ と $R_2$ の合成抵抗を求めるだけです。

 

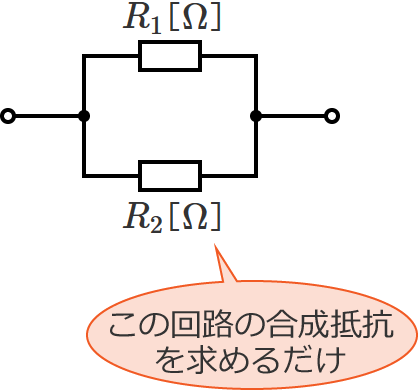
2つの抵抗を並列接続した回路

 

和分の積を使って抵抗 $R_1$ と $R_2$ の合成抵抗 $R$ を求めると、

 

$\therefore R=\dfrac{R_1R_2}{R_1+R_2}$　［$\Omega$］

 

となり、これが回路全体の合成抵抗になります。

 

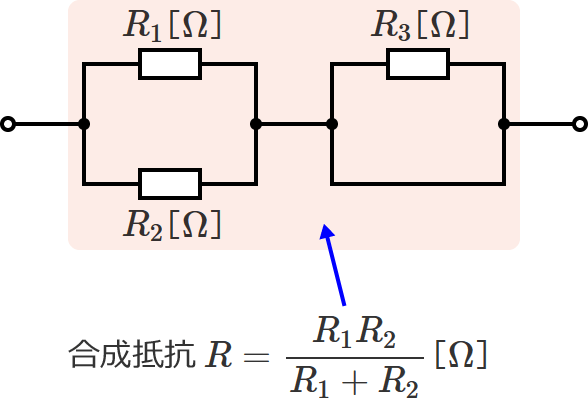
回路の合成抵抗

 

以上のように、短絡されている抵抗がある場合には、短絡されている抵抗を無視して計算する（取り除いて計算する）と合成抵抗を求めることができます。

 

短絡されている抵抗を無視できるのはなぜか？

なぜ、短絡されている抵抗を無視できるのでしょうか？

 

この理由は、回路に流れる電流について考えてみると分かります。

 

次のように回路に直流電源をつなぎ、回路全体に流れる電流を $I$ とします。

 

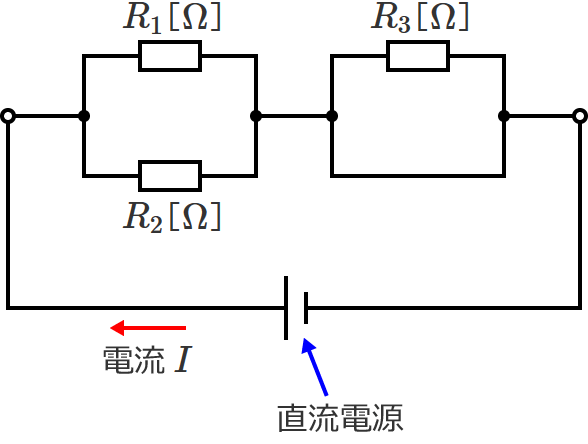
抵抗回路に直流電源をつないだ回路

 

このとき、電流 $I$ は、回路の左側では抵抗 $R_1$ と $R_2$ に分流しますが、回路の右側ではどう流れるでしょうか？

 

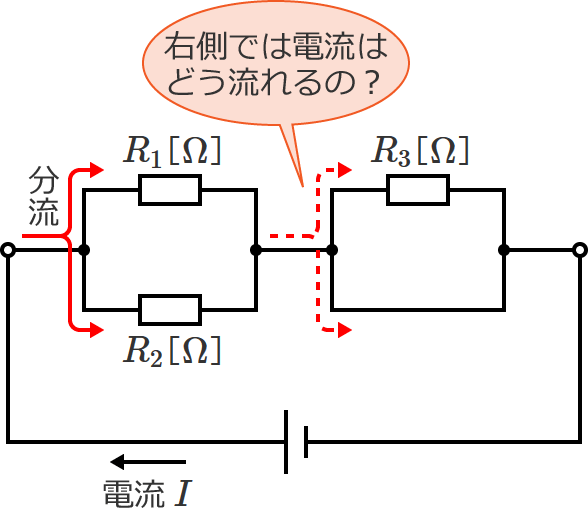
抵抗が短絡されている回路の右側では電流はどう流れるか

 

ここで、回路の右側の電線の抵抗の大きさは無視できるくらい小さいものとして（電線の抵抗の大きさを $0\,\Omega$ と考える）、抵抗 $R_3$ に流れる電流 $I_3$ を計算してみると、

 

$I_3=I\times\dfrac{\text{電線の抵抗}}{R_3+\text{電線の抵抗}}$ $=I\times\dfrac{0}{R_3+0}$ $=\dfrac{0}{R_3}$ $=0$

 

$\therefore I_3=0$　［$\mathrm{A}$］

 

となります。

 

また、電線に流れる電流を計算してみると、

 

電線に流れる電流 $=I\times\dfrac{R_3}{R_3+\text{電線の抵抗}}$ $=I\times\dfrac{R_3}{R_3+0}$ $=I\times\dfrac{R_3}{R_3}$ $=I$

 

$\therefore$ 電線に流れる電流 $=I$　［$\mathrm{A}$］

 

となります。

 

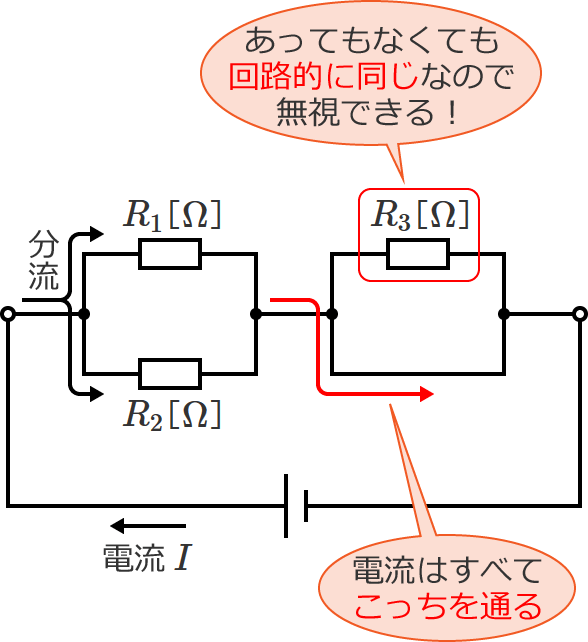
つまり、抵抗の大きさが $0\,\Omega$ の電線で抵抗を短絡すると、抵抗には電流が流れず、電流はすべて電線の方を通ることになります。

 

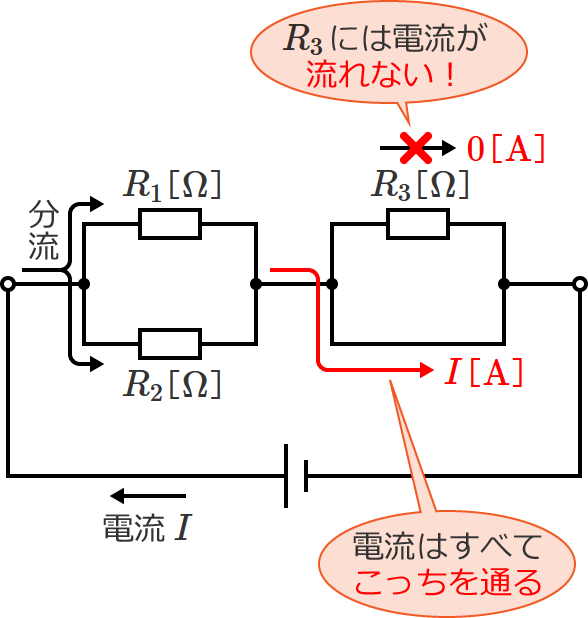
電流はすべて短絡している電線の方を通る

 

なので、短絡されていて電流が流れない抵抗は、あってもなくても回路的に同じなので、無視して考えることができるんです。

 

短絡されていて電流が流れない抵抗は無視できる

 

スポンサーリンク

スポンサーリンク


 

短絡している電線を0Ωの抵抗と考えて合成抵抗を求める方法

次の回路の合成抵抗を、「短絡している電線を $0\,\Omega$ の抵抗と考える方法」で求めてみます。

 

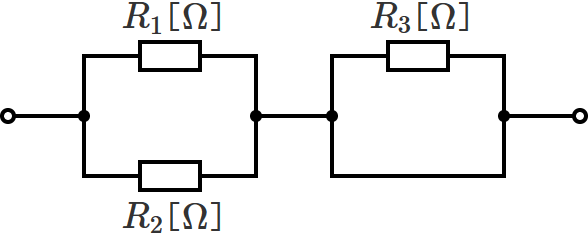
短絡されている抵抗がある回路

 

電気回路の計算をするときには、ふつう、電線の抵抗の大きさは $0\,\Omega$ と考えて計算するので、短絡している電線部分を $0\,\Omega$ の抵抗と考えます。

 

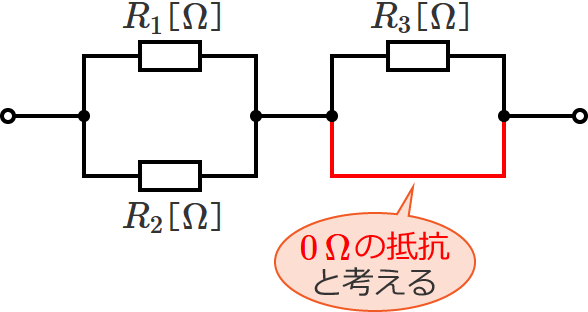
短絡している電線部分を0Ωと考える

 

すると、回路は次のようになります。

 

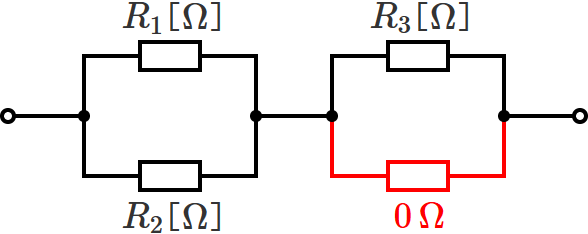
短絡している電線部分を0Ωの抵抗にした回路

 

あとは、この回路の合成抵抗を計算するだけです。

 

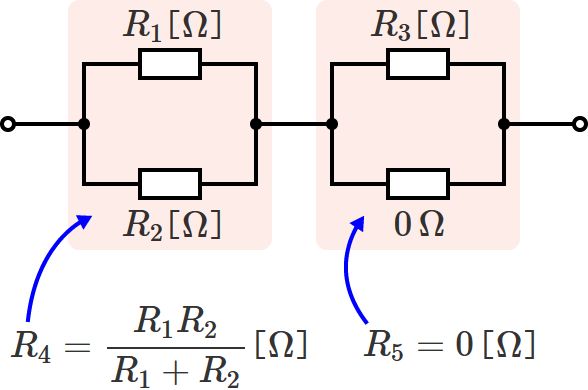
回路の左側の2つの合成抵抗を $R_4$ とすると、$R_4$ は和分の積を使って、

 

$\therefore R_4=\dfrac{R_1R_2}{R_1+R_2}$　［$\Omega$］　…①

 

となります。

 

また、回路の右側の2つの合成抵抗を $R_5$ とすると、$R_5$ は、

 

$R_5=\dfrac{R_3\times\text{電線の抵抗}}{R_3+\text{電線の抵抗}} =\dfrac{R_3\times0}{R_3+0}$ $=\dfrac{0}{R_3}$ $=0$

 

$\therefore R_5=0$　［$\Omega$］　…②

 

となります。

 

R4とR5の合成抵抗値

 

したがって、回路全体の合成抵抗 $R$ は、①と②を足して、

 

$R=R_4+R_5=\dfrac{R_1R_2}{R_1+R_2} +0$ $=\dfrac{R_1R_2}{R_1+R_2}$

 

$\therefore R=\dfrac{R_1R_2}{R_1+R_2}$　［$\Omega$］

 

となります。

 

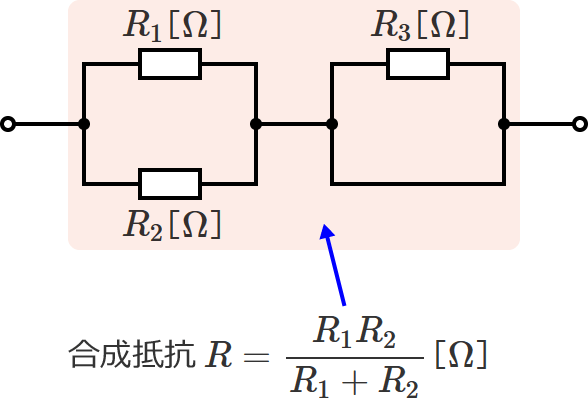
回路の合成抵抗

 

以上のように、短絡されている抵抗がある場合には、短絡している電線の抵抗を $0\,\Omega$ とすると合成抵抗を求めることができます。

 

短絡されている抵抗がある場合の合成抵抗の求め方のまとめ

短絡されている抵抗がある場合の合成抵抗は、次のようにすると求めることができる。

  • 短絡されている抵抗を無視して合成抵抗を計算する

または、

  • 短絡している電線の抵抗を $0\,\Omega$ として合成抵抗を計算する

 

スポンサーリンク

スポンサーリンク


 

合成抵抗の求め方の基本については、こちらの合成抵抗の求め方のページを参考にしてみてください。

 

短絡って？という方は、こちらの短絡（ショート）のページを参考にしてみてください。



スポンサーリンク


短絡されている抵抗がある場合の合成抵抗の求め方　関連ページ

合成抵抗の求め方（計算方法）
合成抵抗の計算は直流回路、交流回路の計算をするときの基本になります。合成抵抗の計算は複雑そうに思えますが、基本的には、抵抗が2個の場合の直列接続または並列接続の合成抵抗の求め方さえ分かっていれば、ほとんどの回路の合成抵抗を求めることができます。
重ね合わせの理
重ね合わせの理について解説しています。重ね合わせの理は、重ね合わせの定理、重ねの理とも呼ばれ、回路に電源が複数ある場合によく使われる定理です。電圧源が2つある回路や、電圧源と電流源が混在した回路などの重ね合わせの理を使った計算方法についても解説していますので参考にしてみてください。
テブナンの定理
テブナンの定理（鳳-テブナンの定理）について解説しています。テブナンの定理は等価電圧源の定理とも呼ばれ、回路の特定の素子に流れる電流を求めるときに有用な定理です。テブナンの定理を使った回路の計算方法や、テブナンの定理の証明についても解説していますので参考にしてみてください。
ノートンの定理
ノートンの定理について解説しています。ノートンの定理は等価電流源の定理とも呼ばれ、回路の特定の素子にかかる電圧を求めるときに有用な定理です。ノートンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。
ミルマンの定理
ミルマンの定理について解説しています。ミルマンの定理は全電圧の定理とも呼ばれ、抵抗と電源の直列接続が複数並列に接続されている回路の端子電圧を求めたいときに有用な定理です。ミルマンの定理の式の導出方法や、ミルマンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。
分圧の法則による直流回路の計算
分圧の法則を使った直流回路の計算方法の例です。分圧の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。
分流の法則による直流回路の計算
分流の法則を使った直流回路の計算方法の例です。分流の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。
ループ解析（基本）
直流回路の計算をするときによく使われる「ループ解析」の方法と基本的な手順について解説しています。ループ解析はキルヒホッフの第二法則（電圧則）を応用した電気回路の計算方法です。
電圧源と電流源の等価変換
電圧源と電流源の等価変換について解説しています。電圧源と電流源が等価になるための条件や、電圧源から電流源、電流源から電圧源への等価変換のやり方などについて解説していますので参考にしてみてください。
電源から供給できる最大電力（最大有能電力）
電源から供給できる最大電力（最大有能電力）について解説しています。内部抵抗をもつ電源は、負荷に供給できる電力に上限（限界）があります。電源からの供給電力が最大になるための条件や、負荷に供給できる電源の最大電力（最大有能電力）などについて解説していますので、参考にしてみてください。
コンデンサの静電容量と電荷の計算の基本（直列接続と並列接続）
コンデンサの静電容量と電荷の計算の基本についてまとめています。コンデンサの計算は、コンデンサ2個を直列接続または並列接続したときの考え方と計算方法が基本になります。
合成静電容量の求め方（計算方法）
合成静電容量の計算は直流回路、交流回路の計算をするときの基本になります。合成静電容量の計算は複雑そうに思えますが、基本的には、コンデンサが2個の場合の直列接続または並列接続の合成静電容量の求め方さえ分かっていれば、ほとんどの回路の合成静電容量を求めることができます。
ジュール熱とジュールの法則
抵抗や金属などの導体に電流が流れたときに発生するジュール熱と、ジュールの法則について解説しています。ジュール熱が発生する理由（原理）についても解説していますので、ジュール熱・ジュールの法則の勉強の参考にしてみてください。