スポンサーリンク
ノートンの定理
※ページ内にPR・広告が含まれる場合があります。
ノートンの定理(ノルトンの定理)は等価電流源の定理とも呼ばれ、電源を含む回路において、ある特定の素子にかかる電圧を求めたいときに有用な定理です。
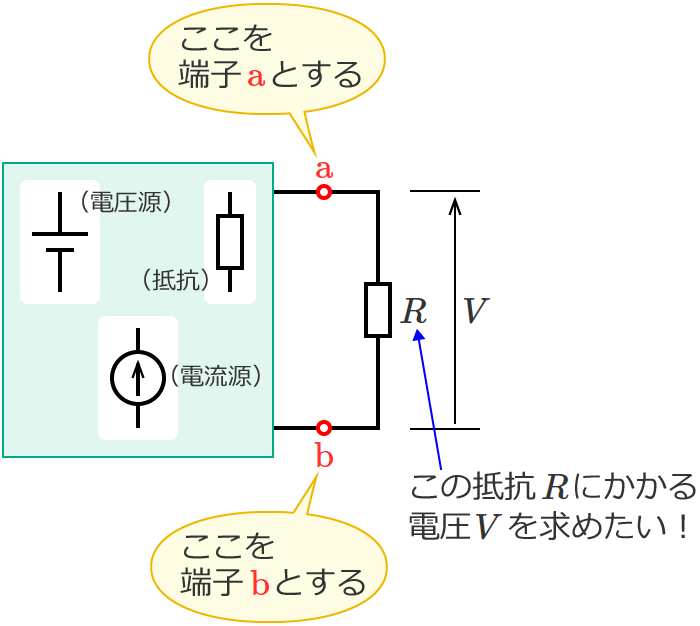
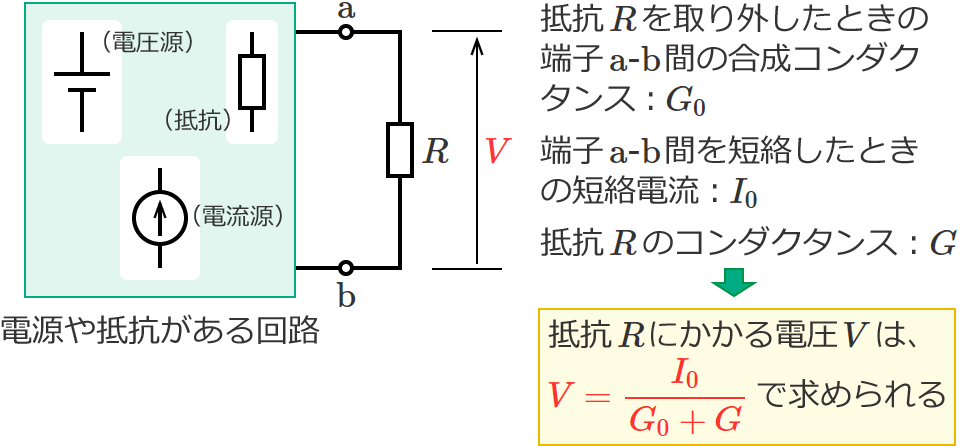
例えば、次のような電源を含む回路があって、この回路の端子 $\mathrm{a}$-$\mathrm{b}$ 間に接続されている抵抗 $R$[$\Omega$] にかかる電圧 $V$[$\mathrm{V}$]を求めたいとします。
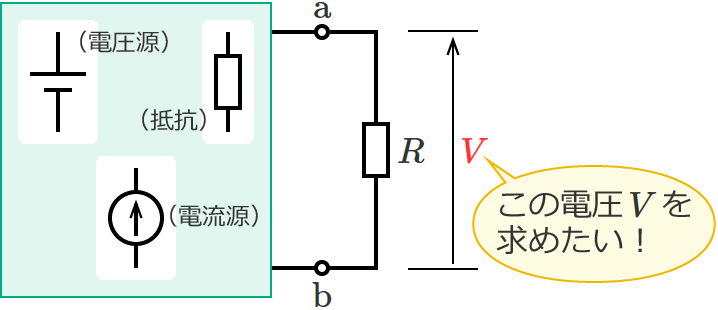
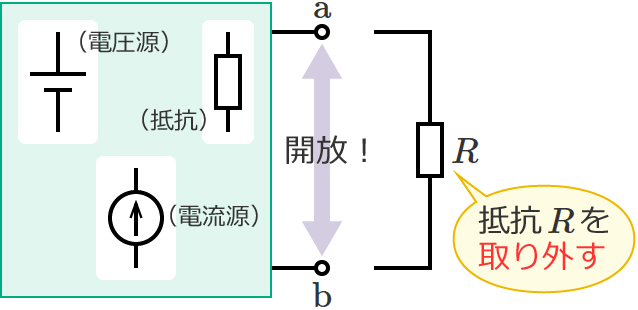
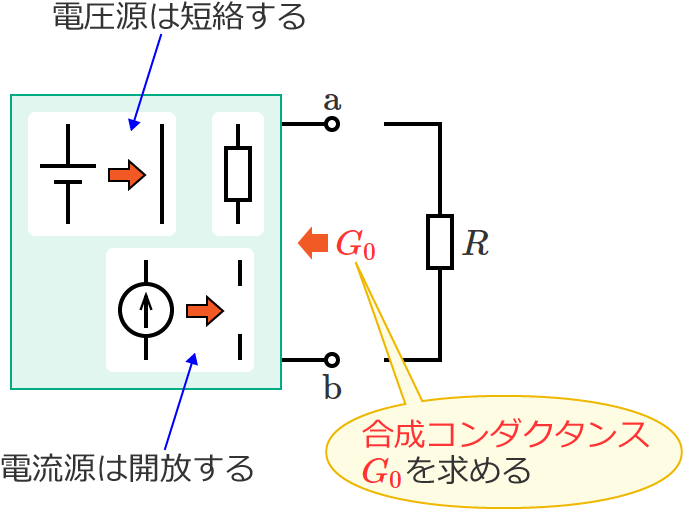
このとき、抵抗 $R$ を取り外して端子 $\mathrm{a}$-$\mathrm{b}$ 間を開放状態にしたときの端子 $\mathrm{a}$-$\mathrm{b}$ 間の合成コンダクタンスを $G_0$[$\mathrm{S}$]、
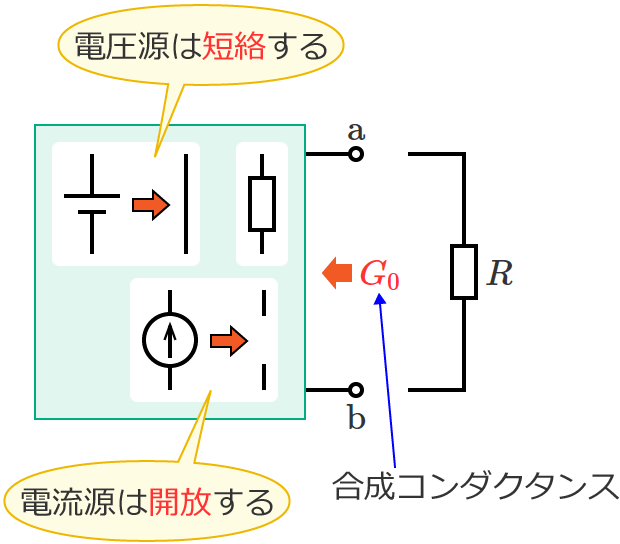
端子 $\mathrm{a}$-$\mathrm{b}$ 間の合成コンダクタンス $G_0$ を求めるときは、電圧源は短絡、電流源は開放します。
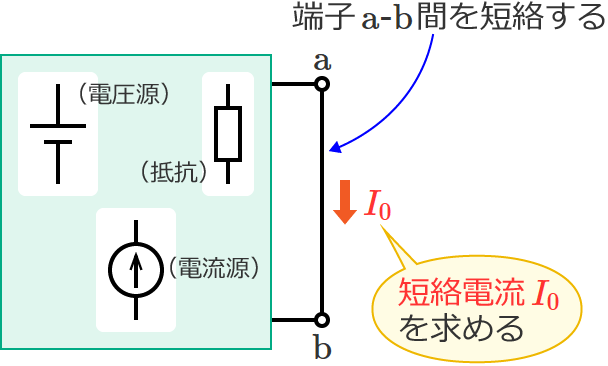
端子 $\mathrm{a}$-$\mathrm{b}$ 間を短絡したときの端子 $\mathrm{a}$-$\mathrm{b}$ 間に流れる電流(短絡電流)を $I_0$[$\mathrm{A}$]とすると、
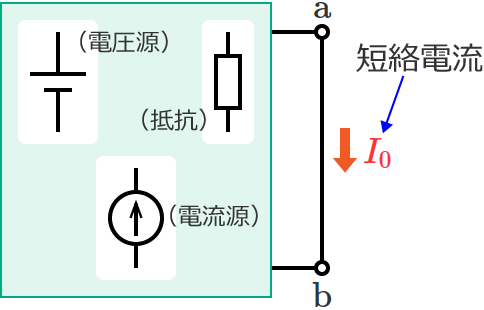
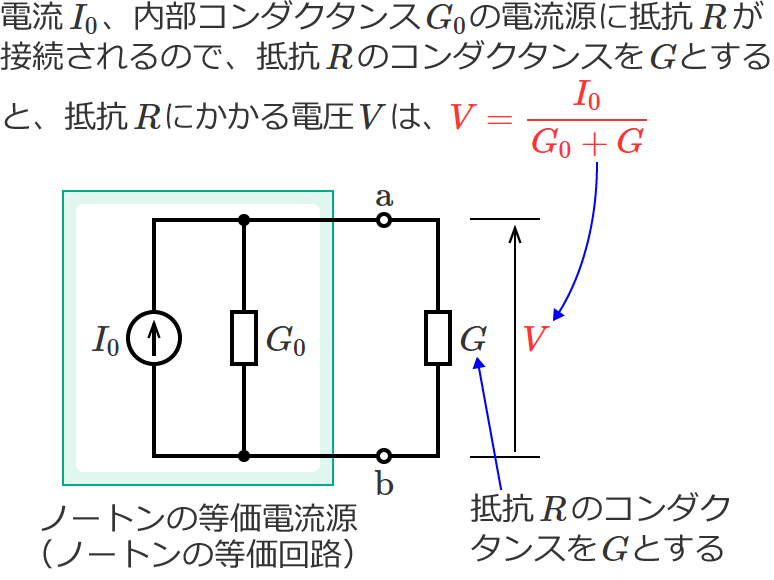
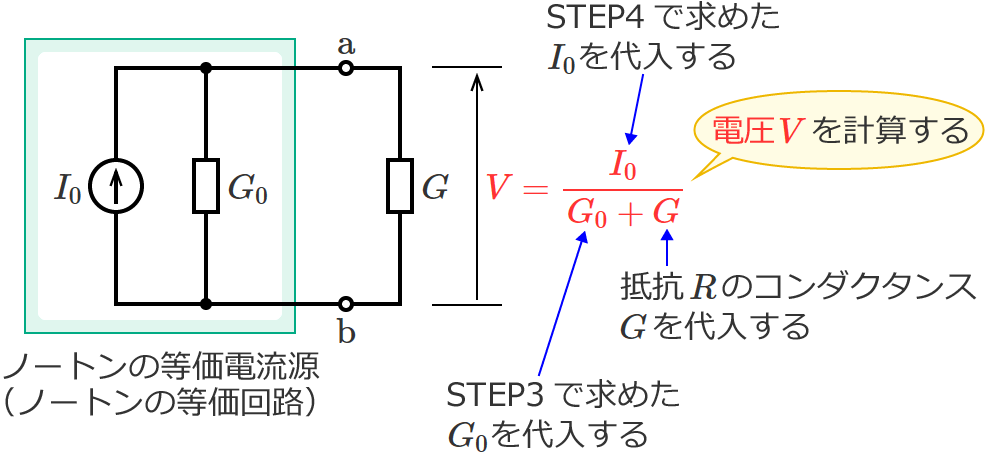
端子 $\mathrm{a}$-$\mathrm{b}$ より左側の回路は、電流が $I_0$ で内部コンダクタンスが $G_0$ の電流源に置き換える(等価変換する)ことができ、
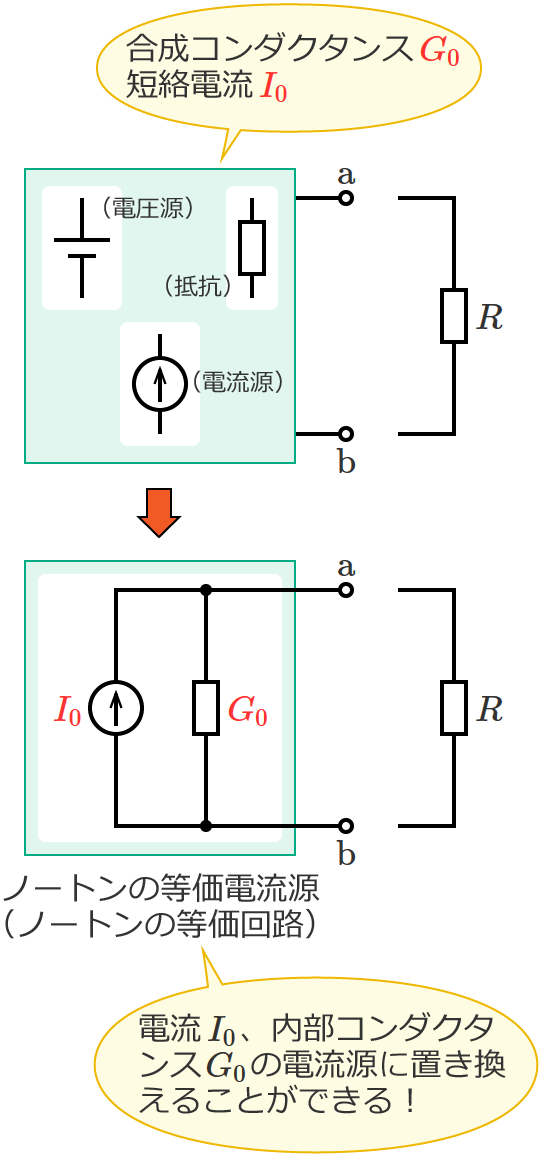
この置き換えた電流源を、ノートンの等価電流源とか、ノートンの等価回路といいます。
抵抗 $R$ にかかる電圧 $V$ は、抵抗 $R$ のコンダクタンスを $G$[$\mathrm{S}$]とすると、次の式で求めることができます。
$V=\dfrac{I_0}{G_0+G}$ …① (ノートンの定理の式)
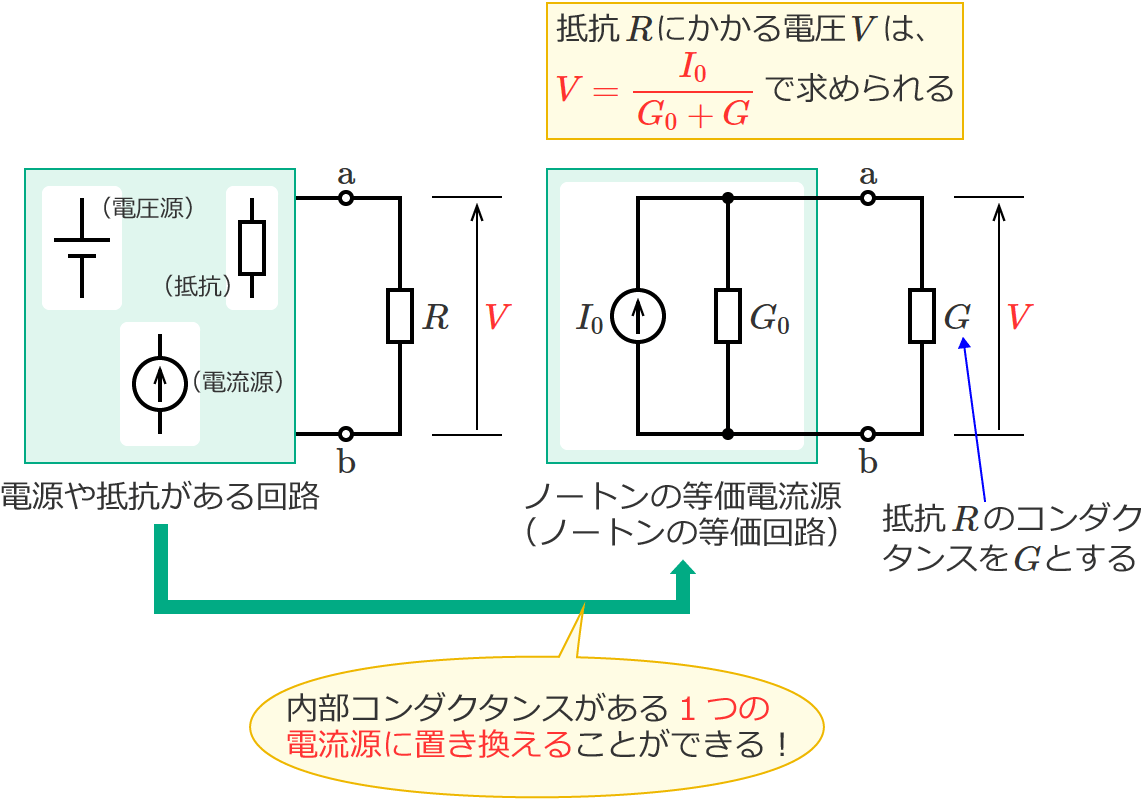
これがノートンの定理で、ノートンの定理を使うと、電圧を求めたいところの特定の素子を除いた部分の回路(この場合、端子 $\mathrm{a}$-$\mathrm{b}$ より左側の回路)を内部コンダクタンスがある1つの電流源で等価的に置き換えることができるので、複雑な回路であっても回路を単純化して電圧の計算をできるようになります。
スポンサーリンク
ノートンの定理による電圧の求め方を整理すると、次のような手順(STEP1〜STEP5)になります。
以上のような手順で、抵抗 $R$ にかかる電圧 $V$ を求めることができます。
では続いて、ノートンの定理の問題でよくある簡単な回路を例にして、抵抗にかかる電圧を求めてみましょう。
このページではノートンの定理を直流回路(電源は直流電源、素子は抵抗のみ)で解説していますが、ノートンの定理は交流回路でも成り立つ定理です。
スポンサーリンク
スポンサーリンク
ノートンの定理による電圧の計算
ここでは、
- 電源が1つ、抵抗が3つある回路
- 電源が2つ、抵抗が3つある回路
の2つの回路について、ノートンの定理を用いて抵抗にかかる電圧を求めてみます。
電源が1つ、抵抗が3つある回路
ノートンの定理を用いて、次の回路の抵抗 $R_3$ にかかる電圧 $V_3$ を先ほどのSTEP1〜5の手順に従って求めてみます。
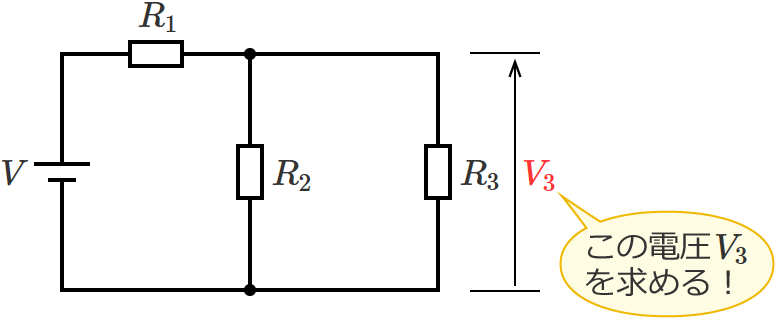
抵抗 $R_3$ にかかる電圧を求めたいので、抵抗 $R_3$ の両端を端子「$\mathrm{a}$」「$\mathrm{b}$」とします。
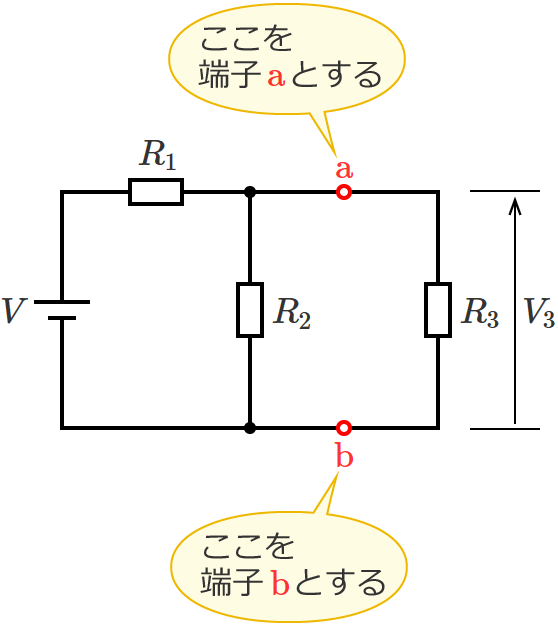
抵抗 $R_3$ を取り外して、端子 $\mathrm{a}$-$\mathrm{b}$ 間を開放状態にします。
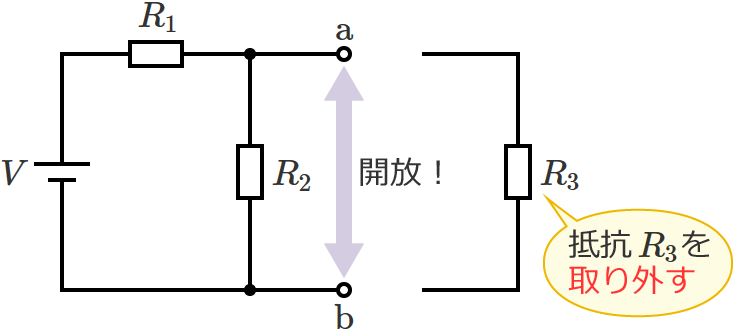
電圧源は短絡し、電流源は開放して回路内のすべての電源を取り除くと、回路は次のようになります。
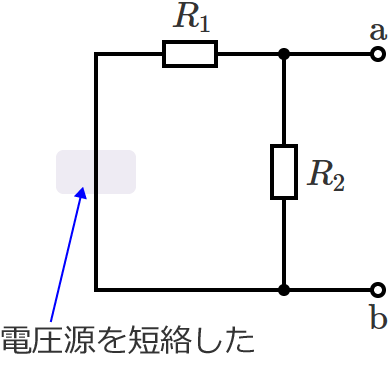
この回路の電源は電圧源だけなので、電圧源を短絡します。
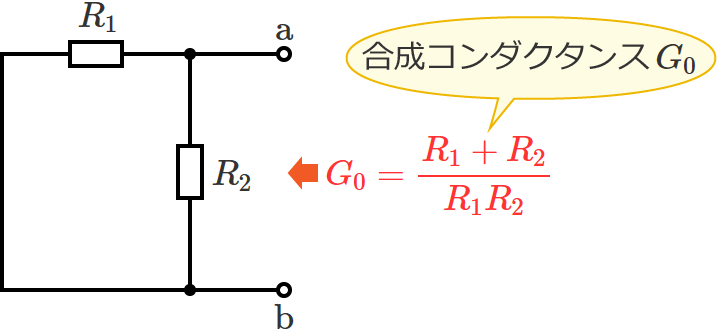
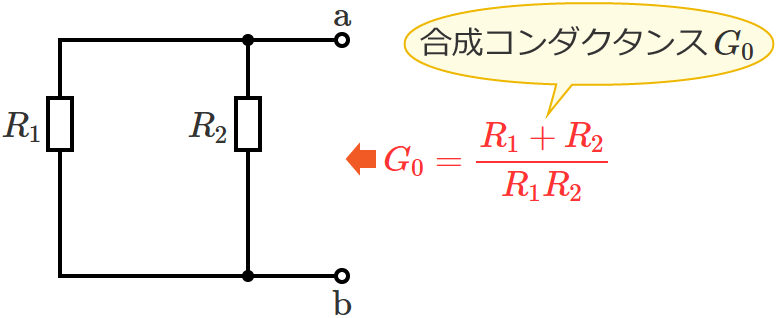
電源を取り除くと抵抗 $R_1$ と抵抗 $R_2$ が並列に接続された回路になっているので、端子 $\mathrm{a}$-$\mathrm{b}$ からみた回路の合成コンダクタンス $G_0$ は、
$G_0=\dfrac{1}{R_1} +\dfrac{1}{R_2} =\dfrac{R_2+R_1}{R_1R_2}$
$\therefore G_0=\dfrac{R_1+R_2}{R_1R_2}$ (合成コンダクタンス $G_0$ )
となります。
抵抗の逆数がコンダクタンスになるので、抵抗 $R_1$ のコンダクタンスは $\dfrac{1}{R_1}$ 、抵抗 $R_2$ のコンダクタンスは $\dfrac{1}{R_2}$ になります。並列接続の合成コンダクタンスは、コンダクタンスをただ単に足すだけで求められるので、抵抗 $R_1$ と抵抗 $R_2$ の合成コンダクタンス $G_0$ は、$G_0=\dfrac{1}{R_1} +\dfrac{1}{R_2}$ となります。
端子 $\mathrm{a}$-$\mathrm{b}$ 間を短絡したときの回路は次のような回路になり、

この回路の抵抗 $R_1$ を通った電流は、抵抗 $R_2$ には流れず、すべて端子 $\mathrm{a}$-$\mathrm{b}$ 間の方に流れます。
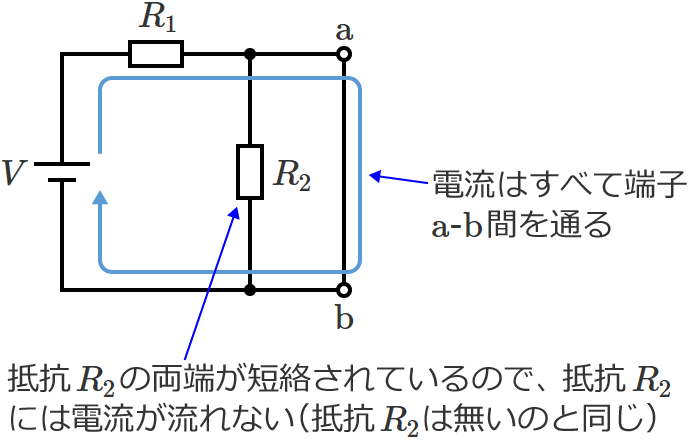
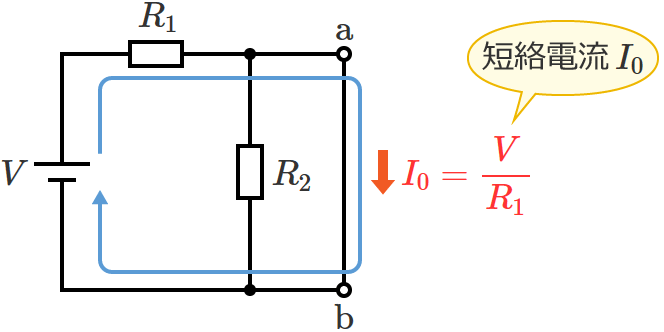
なので、短絡した端子 $\mathrm{a}$-$\mathrm{b}$ 間に流れる電流(短絡電流)$I_0$ はオームの法則より、
$\therefore I_0=\dfrac{V}{R_1}$ (短絡電流 $I_0$ )
となります。
STEP3で求めた合成コンダクタンス $G_0$ とSTEP4で求めた短絡電流 $I_0$ は、
$G_0=\dfrac{R_1+R_2}{R_1R_2}$
$I_0=\dfrac{V}{R_1}$
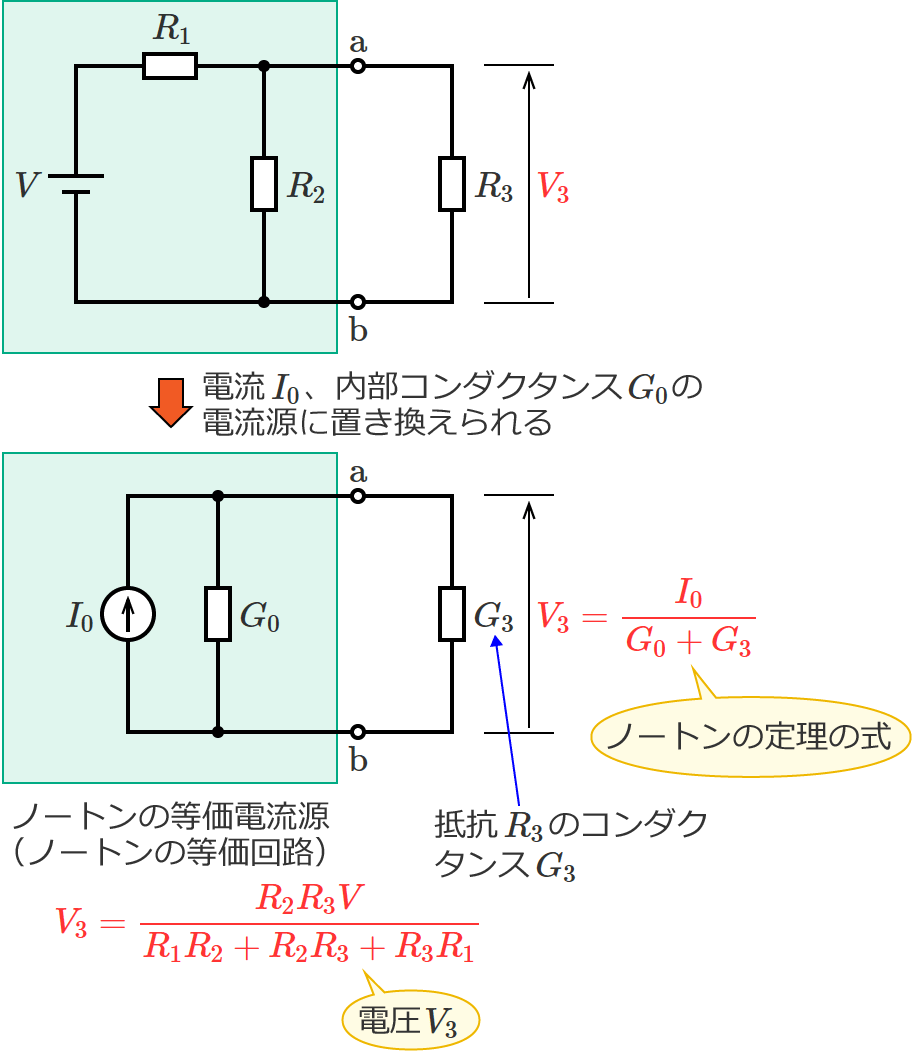
で、端子 $\mathrm{a}$-$\mathrm{b}$ 間の抵抗 $R_3$ のコンダクタンス $G_3$ は $G_3=\dfrac{1}{R_3}$ なので、これらをノートンの定理の式(①式)に代入すると、
$V_3=\dfrac{I_0}{G_0+G_3} =\dfrac{\dfrac{V}{R_1}}{\dfrac{R_1+R_2}{R_1R_2} +\dfrac{1}{R_3}}$
$=\dfrac{\dfrac{V}{R_1}}{\dfrac{\left( R_1+R_2\right) R_3+R_1R_2}{R_1R_2R_3}}$
$=\dfrac{R_2R_3V}{\left( R_1+R_2\right) R_3+R_1R_2}$ (分母と分子に $R_1R_2R_3$ をかけた)
$=\dfrac{R_2R_3V}{R_1R_3+R_2R_3+R_1R_2}$
$\therefore V_3=\dfrac{R_2R_3V}{R_1R_2+R_2R_3+R_3R_1}$ (抵抗 $R_3$ にかかる電圧 $V_3$ )
となり、この電圧 $V_3$ が抵抗 $R_3$ にかかる電圧になります。
以上で、「電源が1つ、抵抗が3つある回路」の抵抗 $R_3$ にかかる電圧 $V_3$ が求められました。
この回路は複雑な回路ではないので、そんなに難しくはないですね。
次は、電源が2つある回路の計算です。電源が2つあるのでちょっとだけ難しくなりますよ、ちょっとだけ。
電源が2つ、抵抗が3つある回路
ノートンの定理を用いて、次の回路の抵抗 $R_3$ にかかる電圧 $V_3$ を求めてみます。
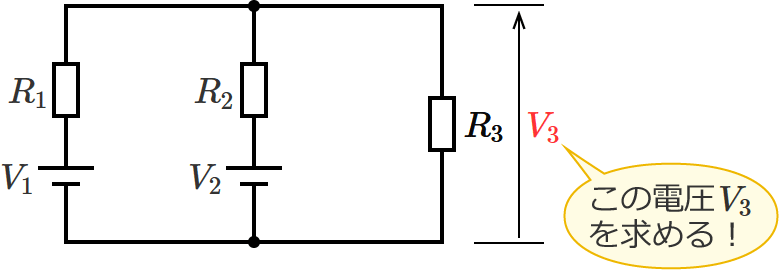
抵抗 $R_3$ にかかる電圧を求めたいので、抵抗 $R_3$ の両端を端子「$\mathrm{a}$」「$\mathrm{b}$」とします。
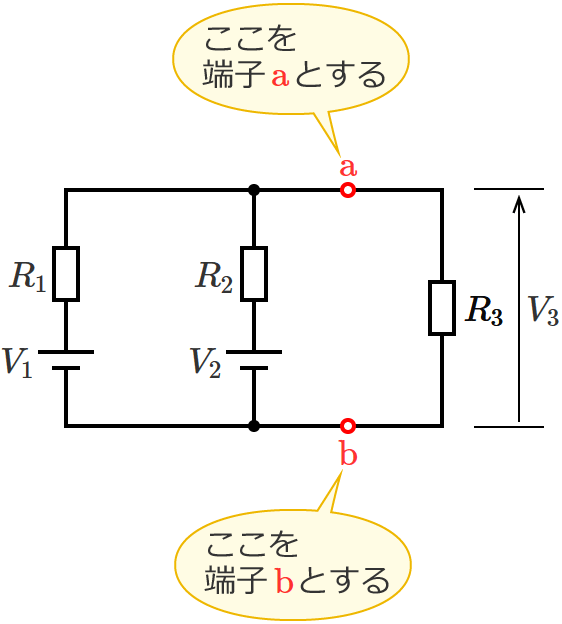
抵抗 $R_3$ を取り外して、端子 $\mathrm{a}$-$\mathrm{b}$ 間を開放状態にします。
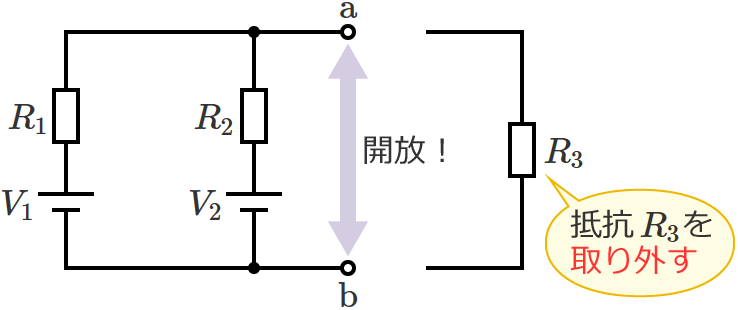
電圧源は短絡し、電流源は開放して回路内のすべての電源を取り除くと、回路は次のようになります。
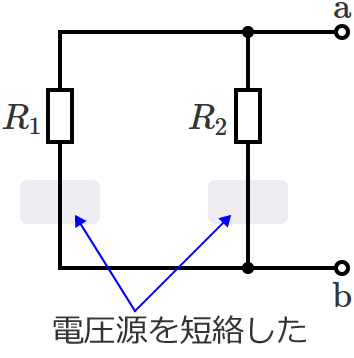
この回路の電源は電圧源だけなので、電圧源を短絡します。
電源を取り除くと抵抗 $R_1$ と抵抗 $R_2$ が並列に接続された回路になっているので、端子 $\mathrm{a}$-$\mathrm{b}$ からみた回路の合成コンダクタンス $G_0$ は、
$G_0=\dfrac{1}{R_1} +\dfrac{1}{R_2} =\dfrac{R_2+R_1}{R_1R_2}$
$\therefore G_0=\dfrac{R_1+R_2}{R_1R_2}$ (合成コンダクタンス $G_0$ )
となります。
端子 $\mathrm{a}$-$\mathrm{b}$ 間を短絡したときの回路は次のようになり、
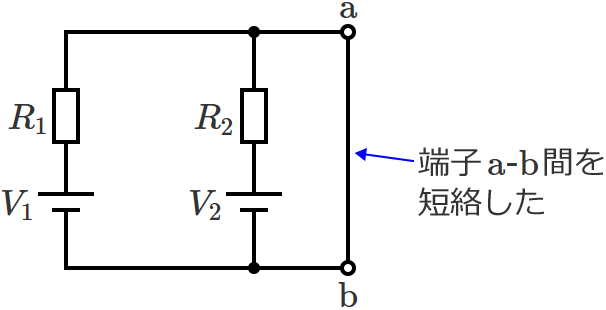
この回路の端子 $\mathrm{a}$-$\mathrm{b}$ 間に流れる電流(短絡電流)$I_0$ は、重ね合わせの理を使うと次のように求められます。
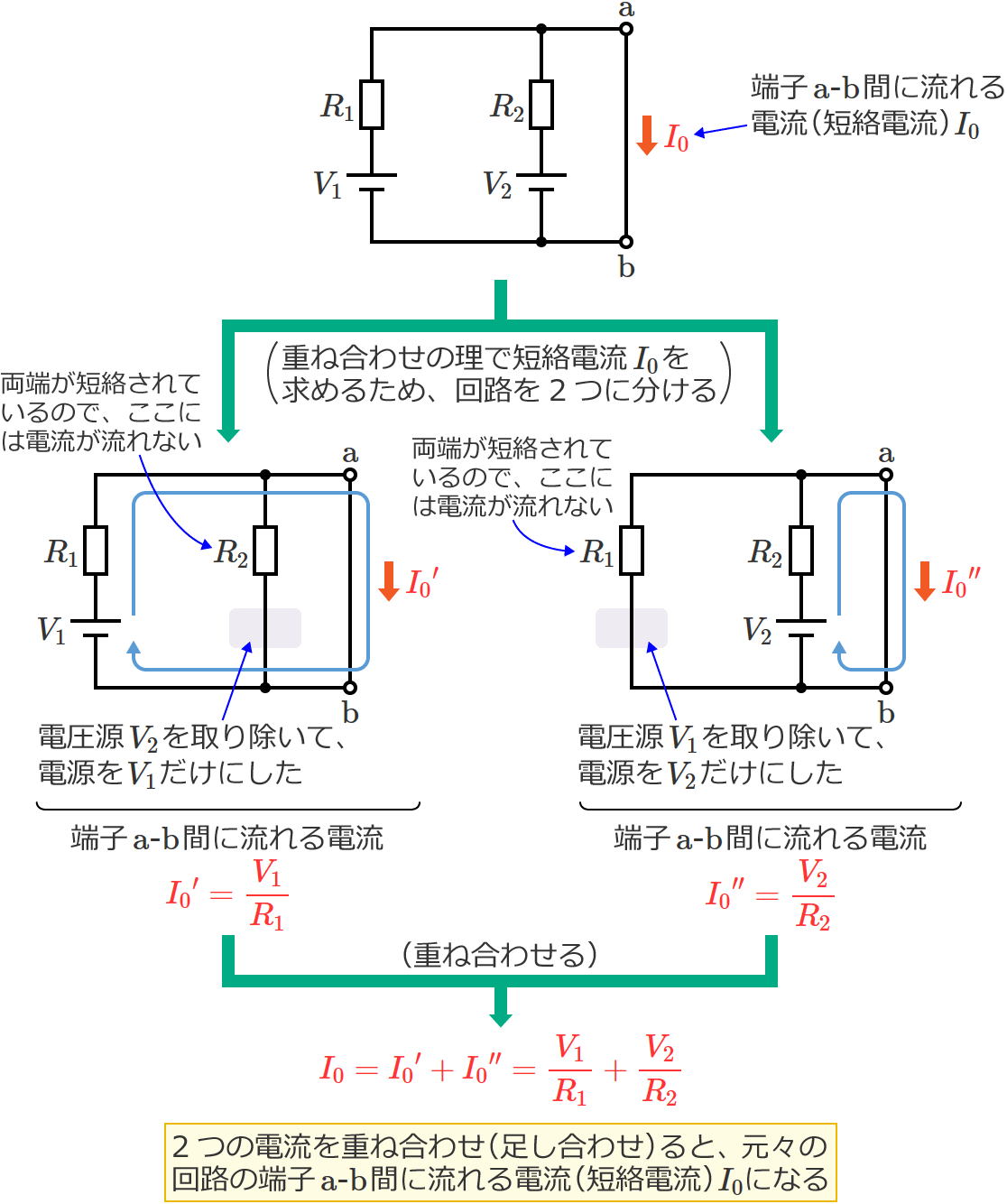
$I_0={I_0}^\prime +{I_0}^{\prime\prime}$
$=\dfrac{V_1}{R_1} +\dfrac{V_2}{R_2} =\dfrac{R_2V_1+R_1V_2}{R_1R_2}$
$\therefore I_0=\dfrac{R_2V_1+R_1V_2}{R_1R_2}$ (短絡電流 $I_0$ )
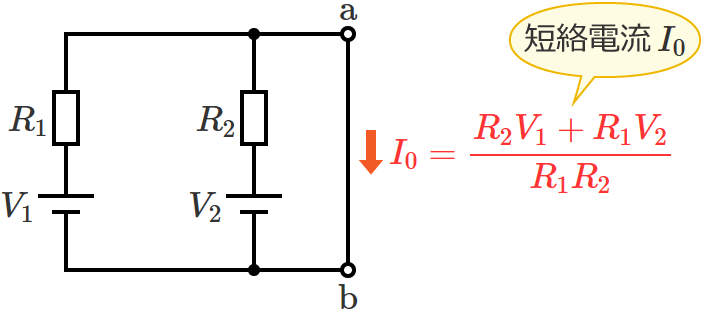
STEP3で求めた合成コンダクタンス $G_0$ とSTEP4で求めた短絡電流 $I_0$ は、
$G_0=\dfrac{R_1+R_2}{R_1R_2}$
$I_0=\dfrac{R_2V_1+R_1V_2}{R_1R_2}$
で、端子 $\mathrm{a}$-$\mathrm{b}$ 間の抵抗 $R_3$ のコンダクタンス $G_3$ は $G_3=\dfrac{1}{R_3}$ なので、これらをノートンの定理の式(①式)に代入すると、
$V_3=\dfrac{I_0}{G_0+G_3} =\dfrac{\dfrac{R_2V_1+R_1V_2}{R_1R_2}}{\dfrac{R_1+R_2}{R_1R_2} +\dfrac{1}{R_3}}$
$=\dfrac{\dfrac{R_2V_1+R_1V_2}{R_1R_2}}{\dfrac{\left( R_1+R_2\right) R_3+R_1R_2}{R_1R_2R_3}}$
$=\dfrac{\left( R_2V_1+R_1V_2\right) R_3}{\left( R_1+R_2\right) R_3+R_1R_2}$ (分母と分子に $R_1R_2R_3$ をかけた)
$=\dfrac{R_2R_3V_1+R_1R_3V_2}{R_1R_3+R_2R_3+R_1R_2}$
$\therefore V_3=\dfrac{R_2R_3V_1+R_1R_3V_2}{R_1R_2+R_2R_3+R_3R_1}$ (抵抗 $R_3$ にかかる電圧 $V_3$ )
となり、この電圧 $V_3$ が抵抗 $R_3$ にかかる電圧になります。
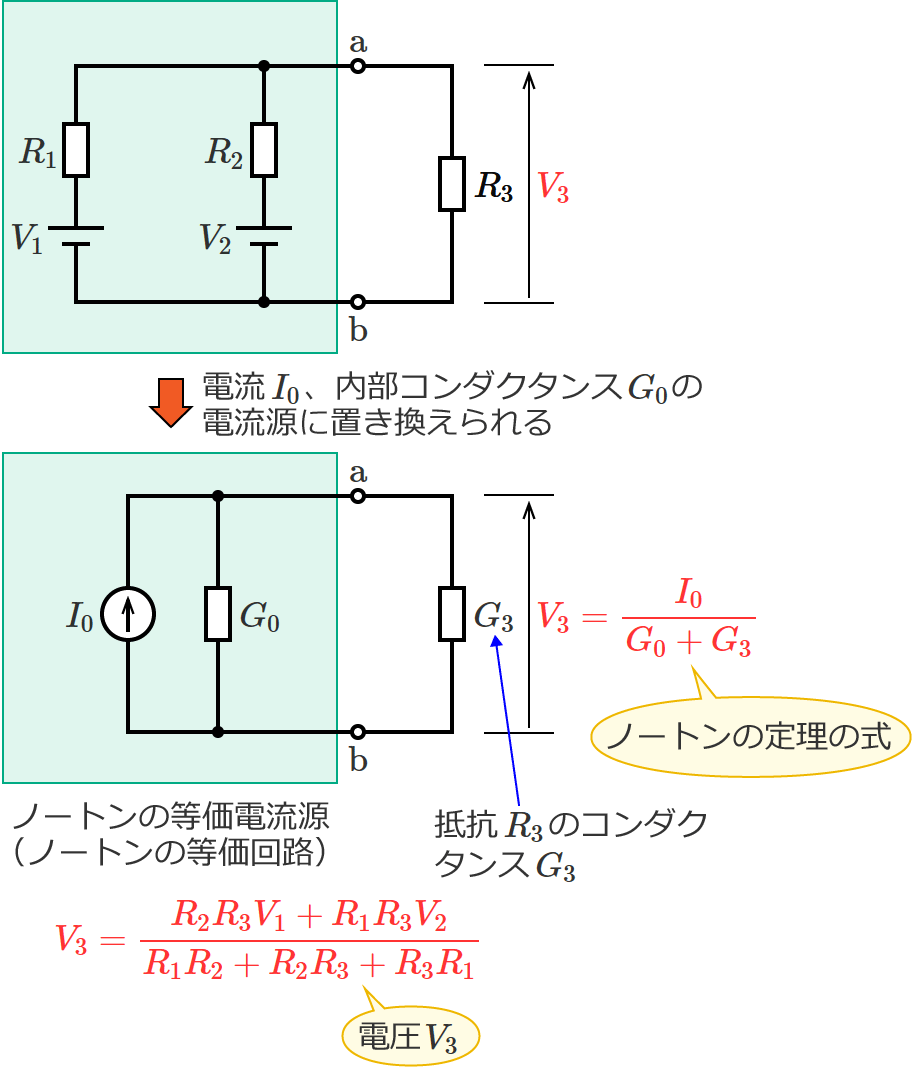
以上で、「電源が2つ、抵抗が3つある回路」の抵抗 $R_3$ にかかる電圧 $V_3$ が求められました。
ノートンの定理はおぼえておくとなにかと役に立つ定理ですので、ノートンの定理の使い方はおぼえておくようにしましょう!
- ノートンの定理は、電源を含む回路において、ある特定の素子にかかる電圧を求めたいときに有用な定理
- 端子間を開放したときの合成コンダクタンス $G_0$(電圧源は短絡し、電流源は開放する)と端子間を短絡したときの短絡電流 $I_0$ が分かれば、$V=\dfrac{I_0}{G_0+G}$ で抵抗 $R$ にかかる電圧 $V$ を求められる
スポンサーリンク
スポンサーリンク
ノートンの定理は回路を「電流源」に置き換える定理ですが、電流源ではなく「電圧源」に置き換える定理をテブナンの定理といいます。テブナンの定理については、こちらのテブナンの定理のページを参考にしてみてください。
スポンサーリンク
ノートンの定理 関連ページ
- 合成抵抗の求め方(計算方法)
- 合成抵抗の計算は直流回路、交流回路の計算をするときの基本になります。合成抵抗の計算は複雑そうに思えますが、基本的には、抵抗が2個の場合の直列接続または並列接続の合成抵抗の求め方さえ分かっていれば、ほとんどの回路の合成抵抗を求めることができます。
- 短絡されている抵抗がある場合の合成抵抗の求め方
- 短絡されている抵抗がある場合の合成抵抗の求め方について解説しています。回路に短絡されている抵抗があるんだけど、どうやって合成抵抗を求めるの?なんてときに参考にしてみてください。
- 重ね合わせの理
- 重ね合わせの理について解説しています。重ね合わせの理は、重ね合わせの定理、重ねの理とも呼ばれ、回路に電源が複数ある場合によく使われる定理です。電圧源が2つある回路や、電圧源と電流源が混在した回路などの重ね合わせの理を使った計算方法についても解説していますので参考にしてみてください。
- テブナンの定理
- テブナンの定理(鳳-テブナンの定理)について解説しています。テブナンの定理は等価電圧源の定理とも呼ばれ、回路の特定の素子に流れる電流を求めるときに有用な定理です。テブナンの定理を使った回路の計算方法や、テブナンの定理の証明についても解説していますので参考にしてみてください。
- ミルマンの定理
- ミルマンの定理について解説しています。ミルマンの定理は全電圧の定理とも呼ばれ、抵抗と電源の直列接続が複数並列に接続されている回路の端子電圧を求めたいときに有用な定理です。ミルマンの定理の式の導出方法や、ミルマンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。
- 分圧の法則による直流回路の計算
- 分圧の法則を使った直流回路の計算方法の例です。分圧の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。
- 分流の法則による直流回路の計算
- 分流の法則を使った直流回路の計算方法の例です。分流の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。
- ループ解析(基本)
- 直流回路の計算をするときによく使われる「ループ解析」の方法と基本的な手順について解説しています。ループ解析はキルヒホッフの第二法則(電圧則)を応用した電気回路の計算方法です。
- 電圧源と電流源の等価変換
- 電圧源と電流源の等価変換について解説しています。電圧源と電流源が等価になるための条件や、電圧源から電流源、電流源から電圧源への等価変換のやり方などについて解説していますので参考にしてみてください。
- 電源から供給できる最大電力(最大有能電力)
- 電源から供給できる最大電力(最大有能電力)について解説しています。内部抵抗をもつ電源は、負荷に供給できる電力に上限(限界)があります。電源からの供給電力が最大になるための条件や、負荷に供給できる電源の最大電力(最大有能電力)などについて解説していますので、参考にしてみてください。
- コンデンサの静電容量と電荷の計算の基本(直列接続と並列接続)
- コンデンサの静電容量と電荷の計算の基本についてまとめています。コンデンサの計算は、コンデンサ2個を直列接続または並列接続したときの考え方と計算方法が基本になります。
- 合成静電容量の求め方(計算方法)
- 合成静電容量の計算は直流回路、交流回路の計算をするときの基本になります。合成静電容量の計算は複雑そうに思えますが、基本的には、コンデンサが2個の場合の直列接続または並列接続の合成静電容量の求め方さえ分かっていれば、ほとんどの回路の合成静電容量を求めることができます。
- ジュール熱とジュールの法則
- 抵抗や金属などの導体に電流が流れたときに発生するジュール熱と、ジュールの法則について解説しています。ジュール熱が発生する理由(原理)についても解説していますので、ジュール熱・ジュールの法則の勉強の参考にしてみてください。


