スポンサーリンク
重ね合わせの理
※ページ内にPR・広告が含まれる場合があります。
重ね合わせの理は、「電源を複数含む回路の任意の部分の電流(または電圧)は、複数の電源それぞれを単独で存在させた場合の電流(または電圧)を重ね合わせたもの(足し合わせたもの)に等しい」という定理です。
重ね合わせの理は、重ね合わせの定理、重ねの理などとも呼ばれています。
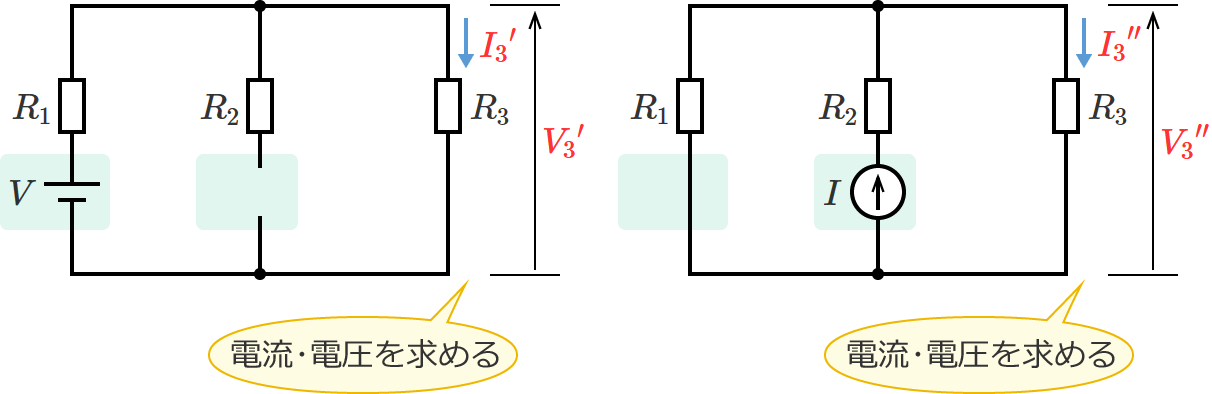
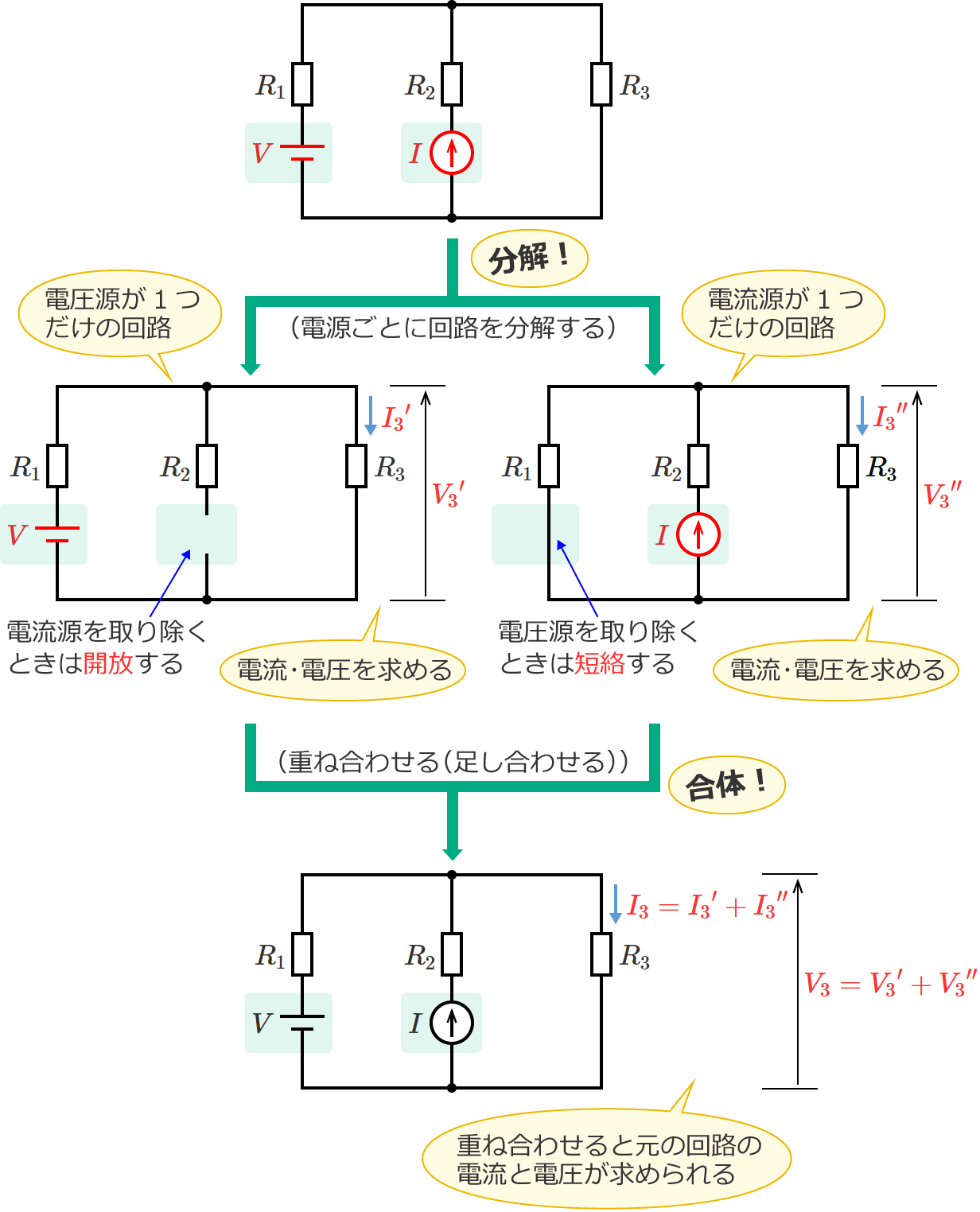
例えば、次の図1のように電源が2つ(電圧源 $V$ と電流源 $I$ )ある回路があるとして、この回路からそれぞれの電源が単独で存在する回路(図1の回路を電源ごとに分解した回路)をつくると、次の図2と図3のようになります。
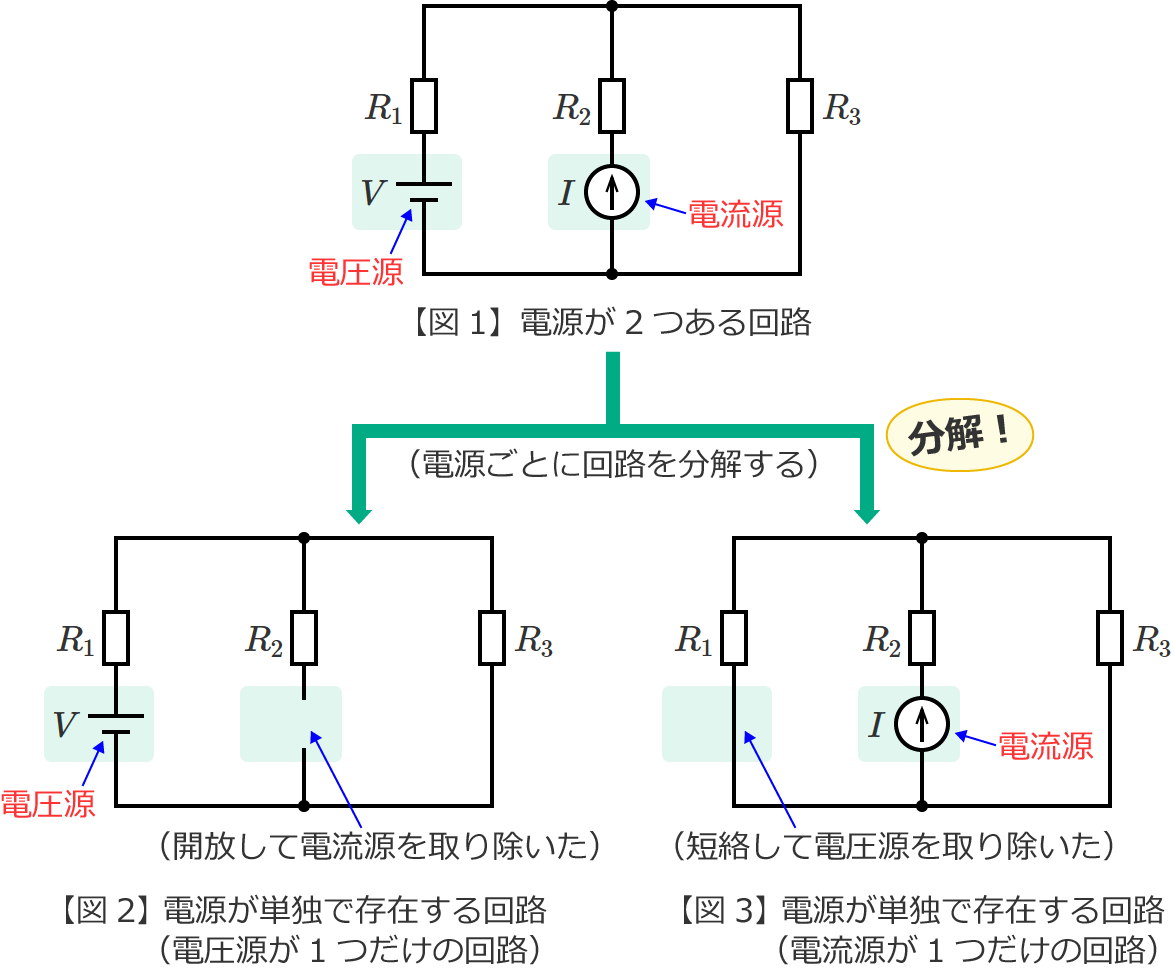
電源が単独で存在する回路(電源ごとに分解した回路)をつくるために残す電源以外の電源を取り除くときは、取り除く電源が電圧源の場合には取り除く電圧源のところを短絡し、取り除く電源が電流源の場合には取り除く電流源のところを開放します。
このとき、図2の回路の抵抗 $R_3$ に流れる電流を ${I_3}^\prime$ 、図2の回路の抵抗 $R_3$ にかかる電圧を ${V_3}^\prime$ とし、図3の回路の抵抗 $R_3$ に流れる電流を ${I_3}^{\prime\prime}$ 、図3の回路の抵抗 $R_3$ にかかる電圧を ${V_3}^{\prime\prime}$ とすると、
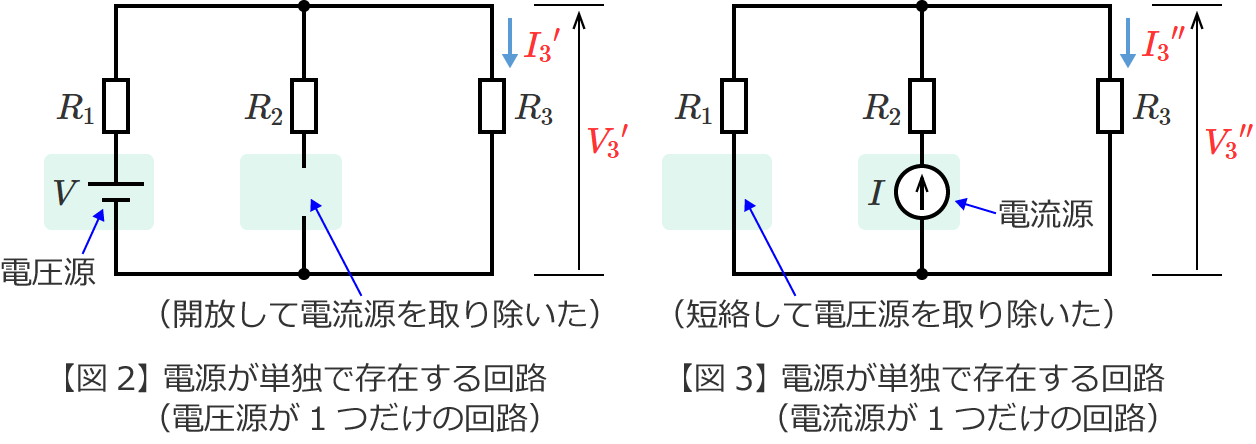
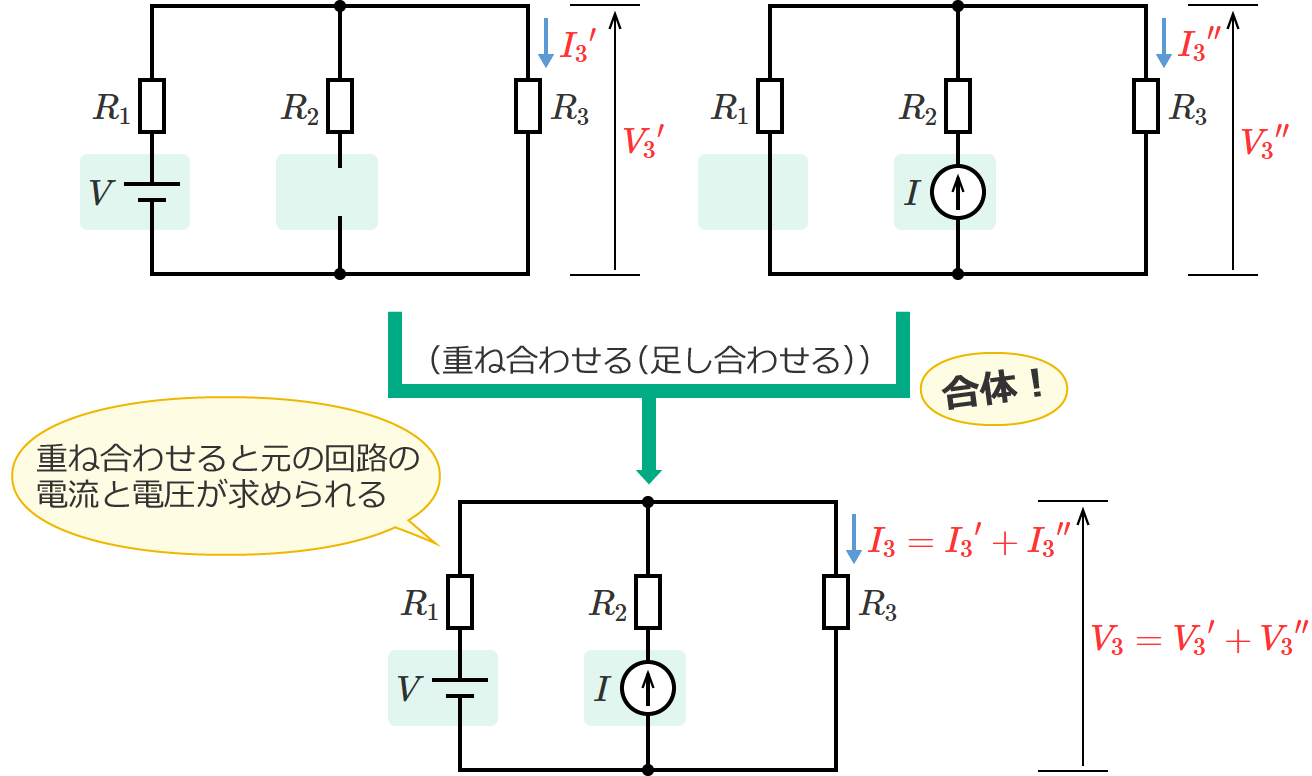
元の回路(図1)の抵抗 $R_3$ に流れる電流 $I_3$ は、図2と図3の回路の抵抗 $R_3$ に流れる電流 ${I_3}^\prime$ と ${I_3}^{\prime\prime}$ を重ね合わせて(足し合わせて)、
$I_3={I_3}^\prime +{I_3}^{\prime\prime}$ (図1の回路の抵抗 $R_3$ に流れる電流 $I_3$ )
となり、元の回路(図1)の抵抗 $R_3$ にかかる電圧 $V_3$ は、図2と図3の回路の抵抗 $R_3$ にかかる電圧 ${V_3}^\prime$ と ${V_3}^{\prime\prime}$ を重ね合わせて(足し合わせて)、
$V_3={V_3}^\prime +{V_3}^{\prime\prime}$ (図1の回路の抵抗 $R_3$ にかかる電圧 $V_3$ )
となります。
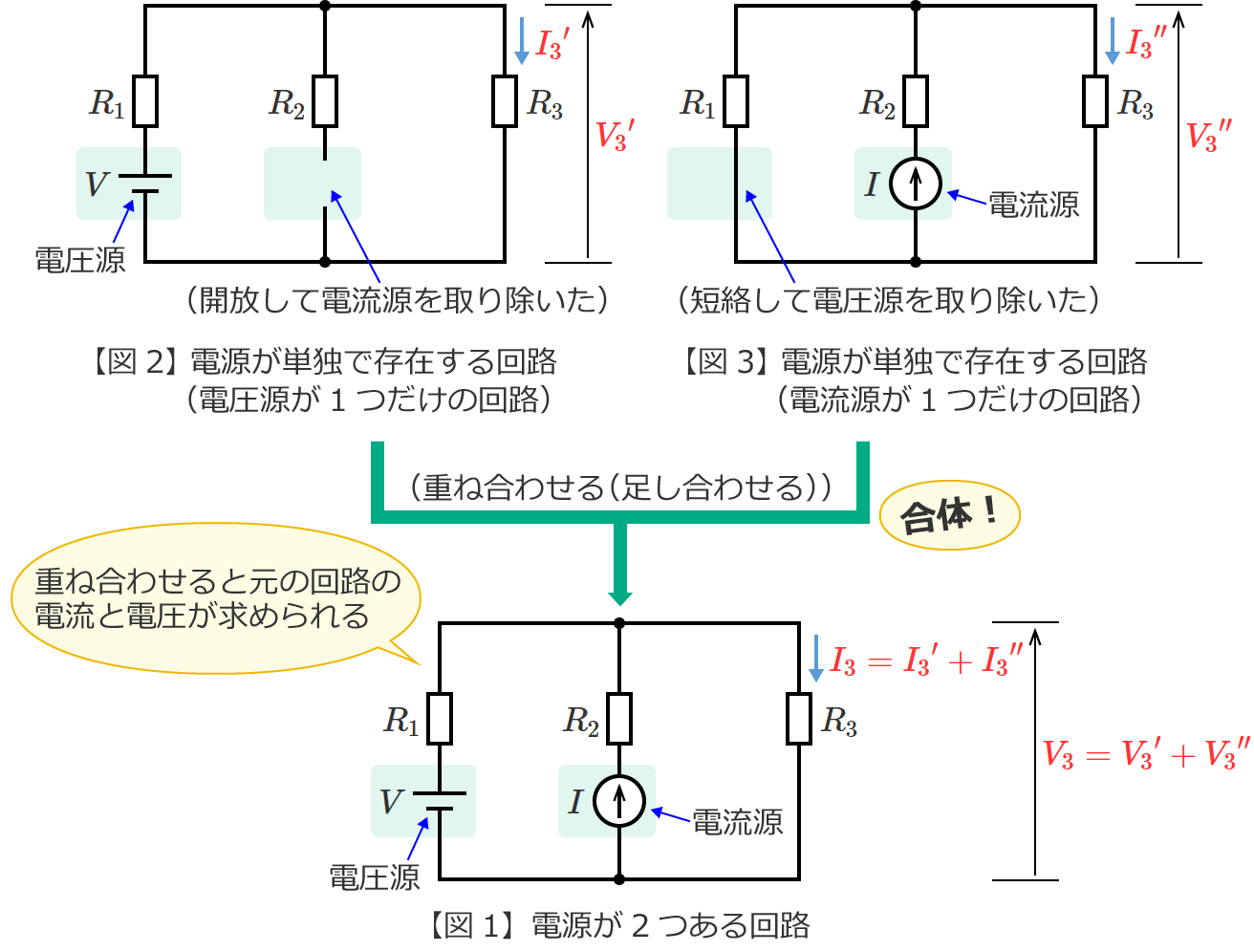
重ね合わせの理を使うと、このように電源を1つだけにして回路の計算ができるので、回路に複数の電源がある場合には、キルヒホッフの法則などの他の計算方法を使うよりも、重ね合わせの理を使った方が回路の計算を簡単にできる場合があります。(計算が簡単になるかどうかは、回路によります。)
スポンサーリンク
重ね合わせの理による回路の計算手順を整理すると、次のような手順(STEP1〜STEP3)になります。
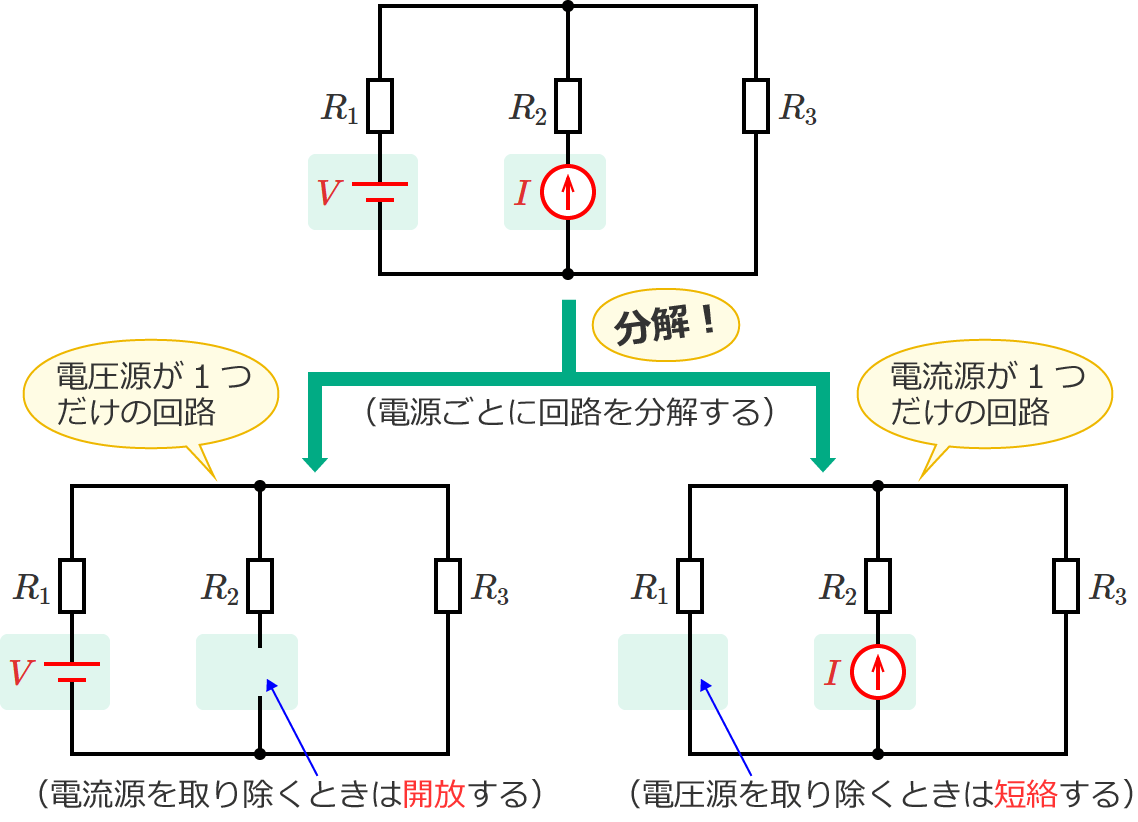
分解される回路の個数は、電源の個数が2つなら2つ、電源の個数が3つなら3つというように、基本的には電源の個数と同じになります。ここでは、電圧源が1つ、電流源が1つの回路を例にして解説しているので、分解される回路の個数は「2」になります。
以上のような手順で、重ね合わせの理による回路の計算ができます。
では続いて、重ね合わせの理の問題でよくある回路を例にして、重ね合わせの理による回路の計算をしてみましょう。
いくつか計算してみると重ね合わせの理に慣れてきて、計算のやり方をおぼえられるようになりますよ!
このページでは重ね合わせの理を直流回路(電源は直流電源、素子は抵抗のみ)で解説していますが、重ね合わせの理は交流回路でも成り立つ定理です。
スポンサーリンク
スポンサーリンク
重ね合わせの理による回路の計算
ここでは、
- 電圧源が2つ(直列)、抵抗が1つある回路
- 電流源が2つ(並列)、抵抗が1つある回路
- 電圧源が2つ(並列)、抵抗が3つある回路
- 電圧源と電流源が混在している回路
の4つの回路について、重ね合わせの理を用いて回路の計算をしてみます。
電圧源が2つ(直列)、抵抗が1つある回路
重ね合わせの理を用いて、次の回路の抵抗 $R$[$\Omega$]に流れる電流 $I$[$\mathrm{A}$]を先ほどのSTEP1〜3の手順に従って求めてみます。
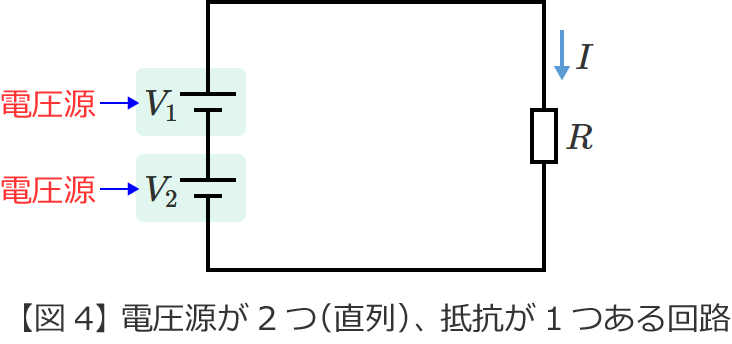
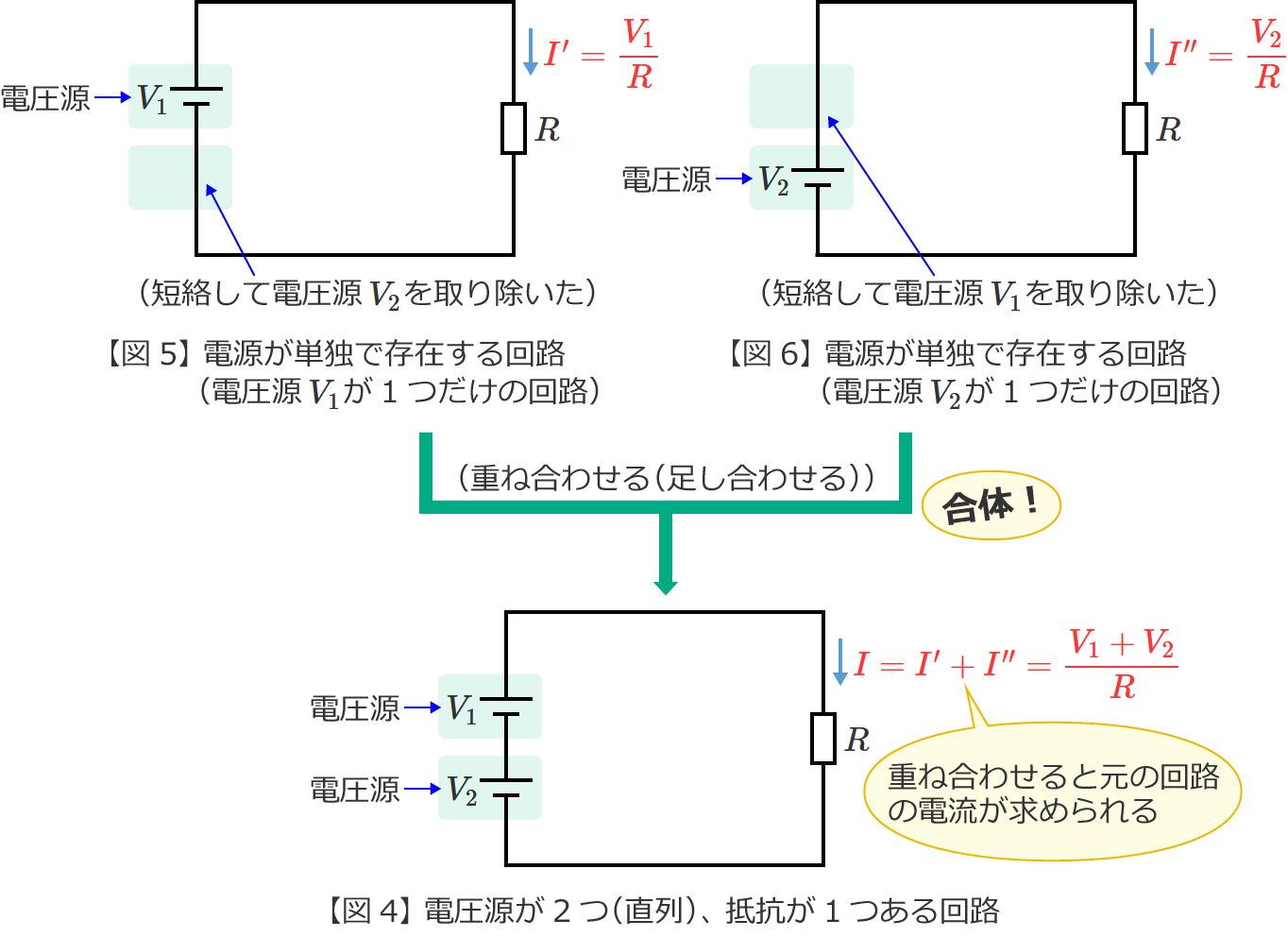
図4の回路からそれぞれの電源が単独で存在する場合の回路(図4の回路を電源ごとに分解した回路)をつくると、次の図5(電圧源 $V_1$ が単独で存在する回路)と図6(電圧源 $V_2$ が単独で存在する回路)のようになります。
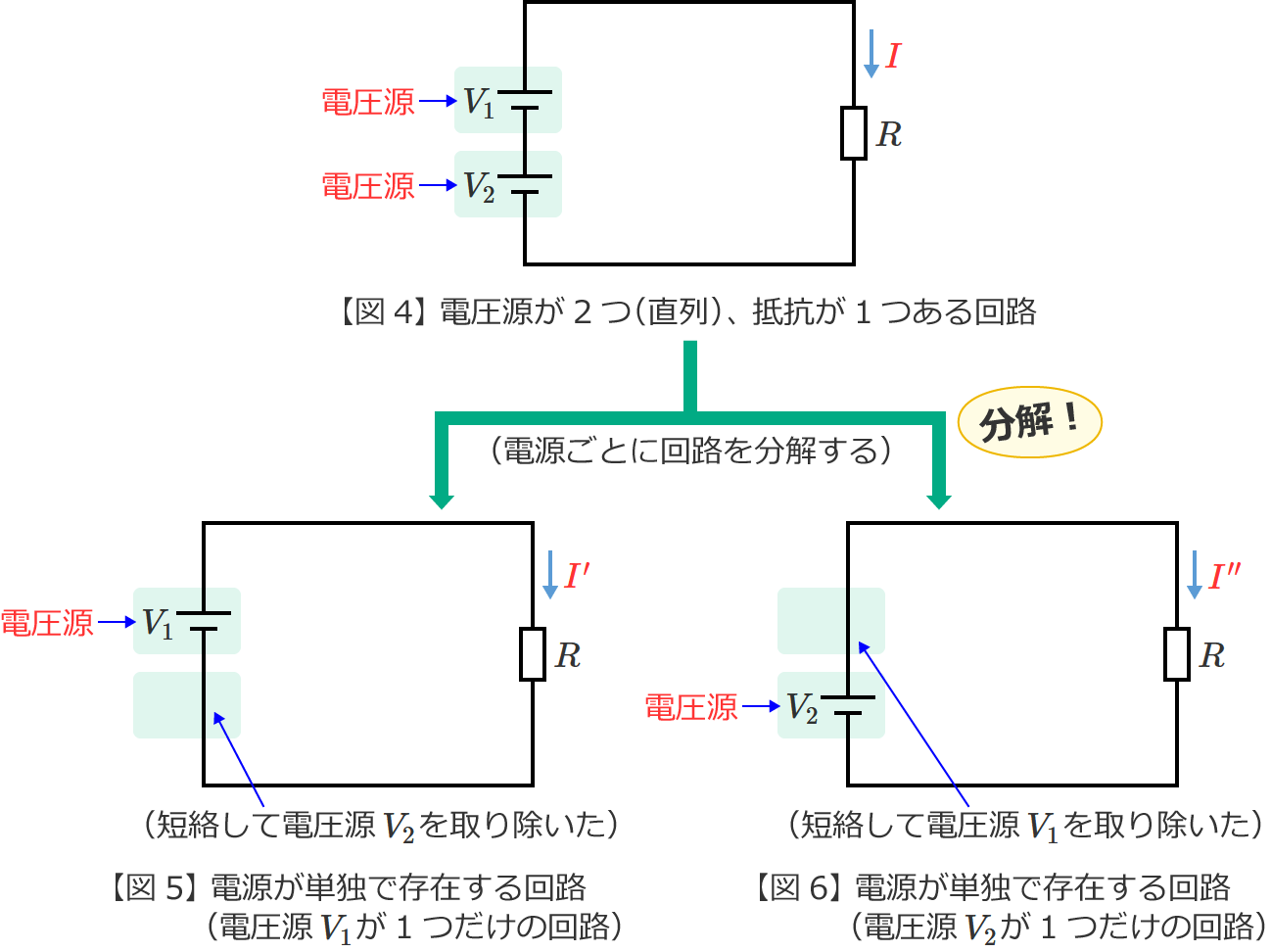
図5の回路の抵抗 $R$ に流れる電流 ${I}^\prime$ は、オームの法則より、
${I}^\prime =\dfrac{V_1}{R}$ (図5の回路の電流 ${I}^\prime$ )
となります。
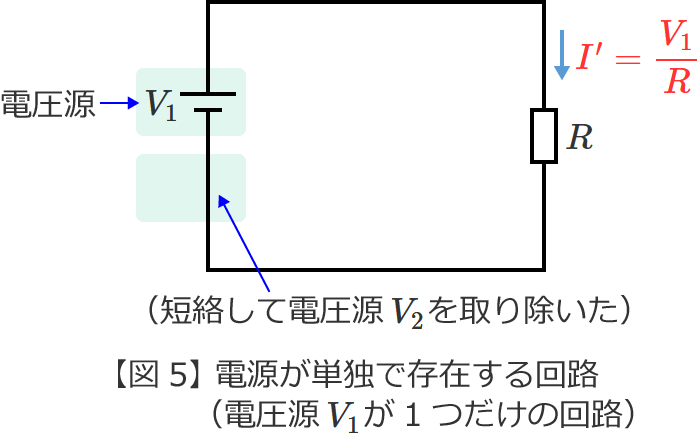
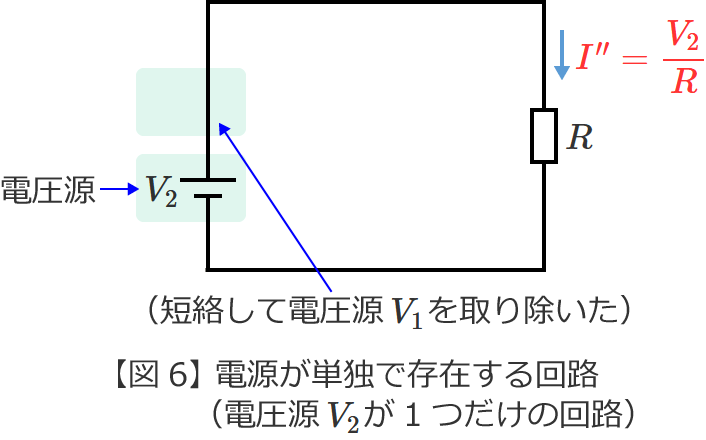
また、図6の回路の抵抗 $R$ に流れる電流 ${I}^{\prime\prime}$ は、こちらもオームの法則より、
${I}^{\prime\prime} =\dfrac{V_2}{R}$ (図6の回路の電流 ${I}^{\prime\prime}$ )
となります。
STEP2で求めた電流 ${I}^\prime$ は ${I}^\prime =\dfrac{V_1}{R}$ 、電流 ${I}^{\prime\prime}$ は ${I}^{\prime\prime} =\dfrac{V_2}{R}$ でしたので、これらを重ね合わせて(足し合わせて)元の回路(図4)の抵抗 $R$ に流れる電流 $I$ を求めると、
${I}={I}^\prime +{I}^{\prime\prime}$ (電流 ${I}^\prime$ と ${I}^{\prime\prime}$ を重ね合わせた )
$=\dfrac{V_1}{R} +\dfrac{V_2}{R}$
$\therefore I=\dfrac{V_1+V_2}{R}$ (図4の回路の電流 $I$ )
となります。
以上で、「電圧源が2つ(直列)、抵抗が1つある回路」(図4)の抵抗 $R$ に流れる電流 $I$ が求められました。
ちなみに、この回路の電流 $I$ は、重ね合わせの理を使わずに次のように単純にオームの法則で解いた方が計算が早くて簡単です。
図4の回路は、電圧 $V_1+V_2$ の電源(電圧源)に抵抗 $R$ が接続された回路なので、

オームの法則より回路に流れる電流 $I$(すなわち、抵抗 $R$ に流れる電流)は、
$I=\dfrac{V_1+V_2}{R}$ (図4の回路の電流 $I$ )
と求められます。回路図をみるとすぐに分かると思いますが、この回路の場合は単純にこれだけで解けるんです。
このページは重ね合わせの理の解説ページなので、図4の回路を重ね合わせの理を使って解きましたが、回路の計算方法には色々あります。回路の計算をするときは、他に簡単な計算方法がないか考えてみるようにしましょう。
次は、「電流源が2つ(並列)、抵抗が1つある回路」の計算です。
電流源が2つ(並列)、抵抗が1つある回路
重ね合わせの理を用いて、次の回路の抵抗 $R$[$\Omega$]に流れる電流 $I$[$\mathrm{A}$]を先ほどのSTEP1〜3の手順に従って求めてみます。
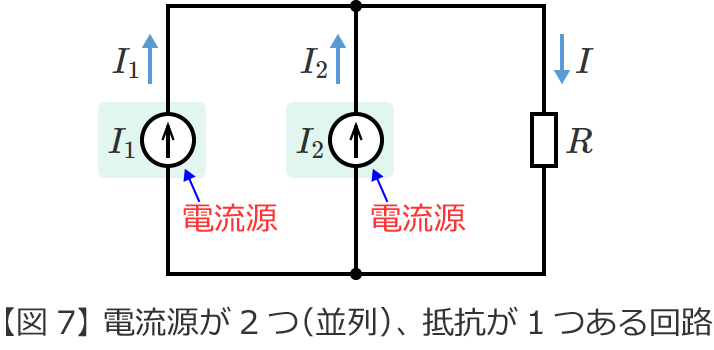
図7の回路からそれぞれの電源が単独で存在する場合の回路(図7の回路を電源ごとに分解した回路)をつくると、次の図8(電流源 $I_1$ が単独で存在する回路)と図9(電流源 $I_2$ が単独で存在する回路)のようになります。
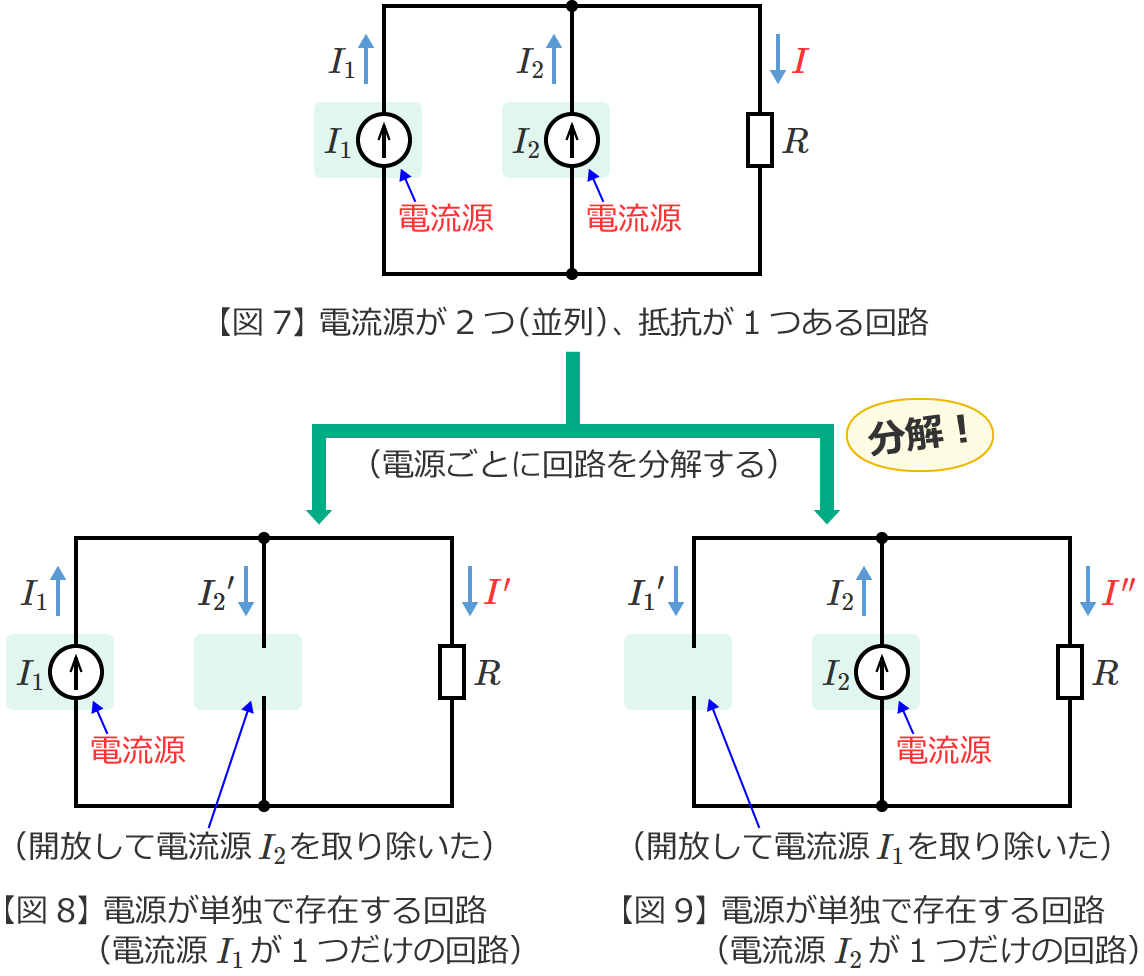
図8の回路の抵抗 $R$ に流れる電流 ${I}^\prime$ は、電流源 $I_1$ の電流がそのまま抵抗 $R$ に流れるので、
${I}^\prime =I_1$ (図8の回路の電流 ${I}^\prime$ )
となります。
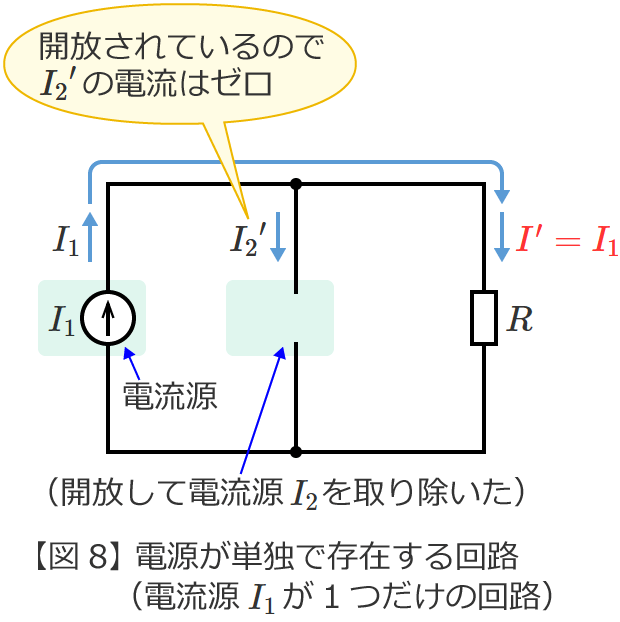
また、図9の回路の抵抗 $R$ に流れる電流 ${I}^{\prime\prime}$ は、電流源 $I_2$ の電流がそのまま抵抗 $R$ に流れるので、
${I}^{\prime\prime} =I_2$ (図9の回路の電流 ${I}^{\prime\prime}$ )
となります。
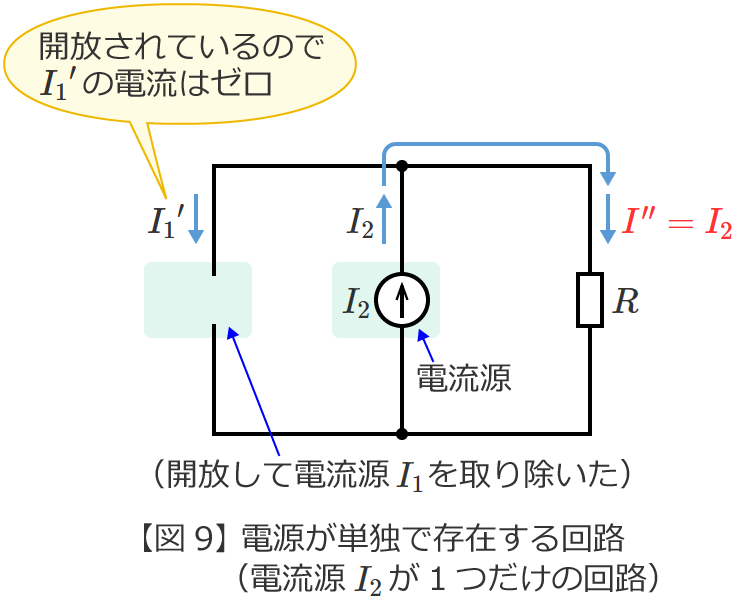
STEP2で求めた電流 ${I}^\prime$ は ${I}^\prime =I_1$ 、電流 ${I}^{\prime\prime}$ は ${I}^{\prime\prime} =I_2$ でしたので、これらを重ね合わせて(足し合わせて)元の回路(図7)の抵抗 $R$ に流れる電流 $I$ を求めると、
$I={I}^\prime +{I}^{\prime\prime}$ (電流 ${I}^\prime$ と ${I}^{\prime\prime}$ を重ね合わせた )
$=I_1+I_2$
$\therefore I=I_1+I_2$ (図7の回路の電流 $I$ )
となります。
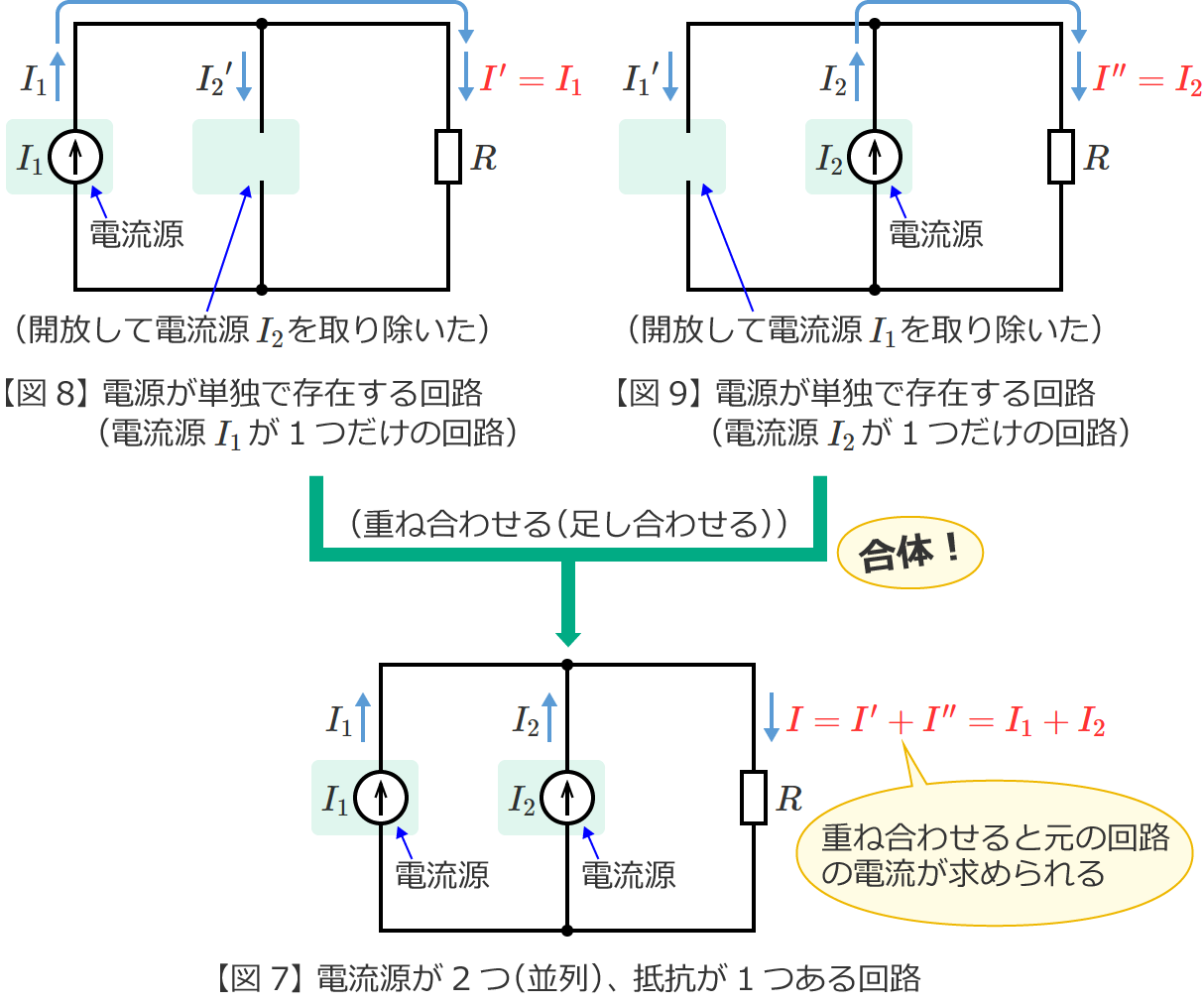
以上で、「電流源が2つ(並列)、抵抗が1つある回路」(図7)の抵抗 $R$ に流れる電流 $I$ が求められました。
この回路の場合、電流源 $I_1$ と $I_2$ の2つの電流源の電流がそのまま抵抗 $R$ に流れるだけなので、回路を見ただけで電流 $I$ は $I=I_1+I_2$ になるのは分かるんですけどね。重ね合わせの理で解くとこうなるよ、みたいな…。
次はもうちょっとそれっぽく、「電圧源が2つ(並列)、抵抗が3つある回路」の計算です。
電圧源が2つ(並列)、抵抗が3つある回路
重ね合わせの理を用いて、次の回路の抵抗 $R_1$[$\Omega$]に流れる電流 $I_1$[$\mathrm{A}$]、抵抗 $R_2$[$\Omega$]に流れる電流 $I_2$[$\mathrm{A}$]、抵抗 $R_3$[$\Omega$]に流れる電流 $I_3$[$\mathrm{A}$]を求めてみます。
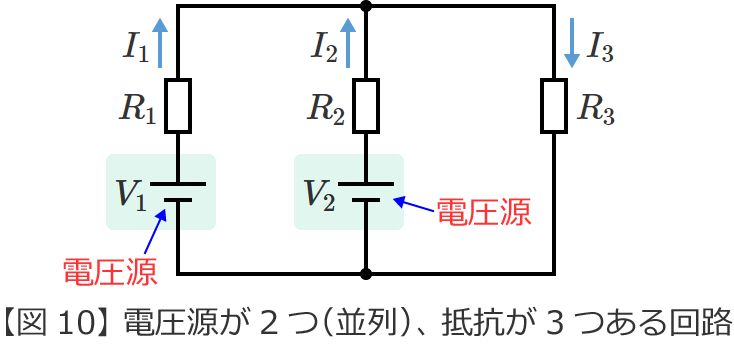
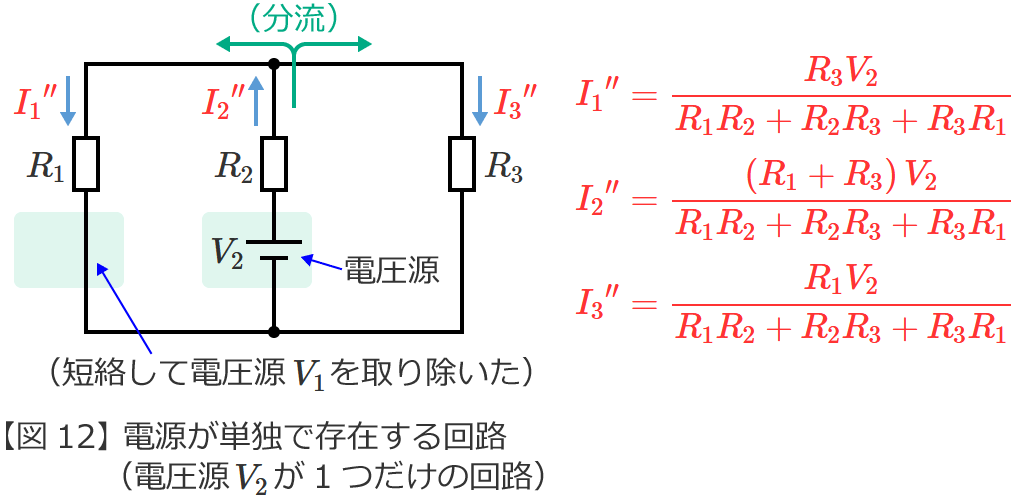
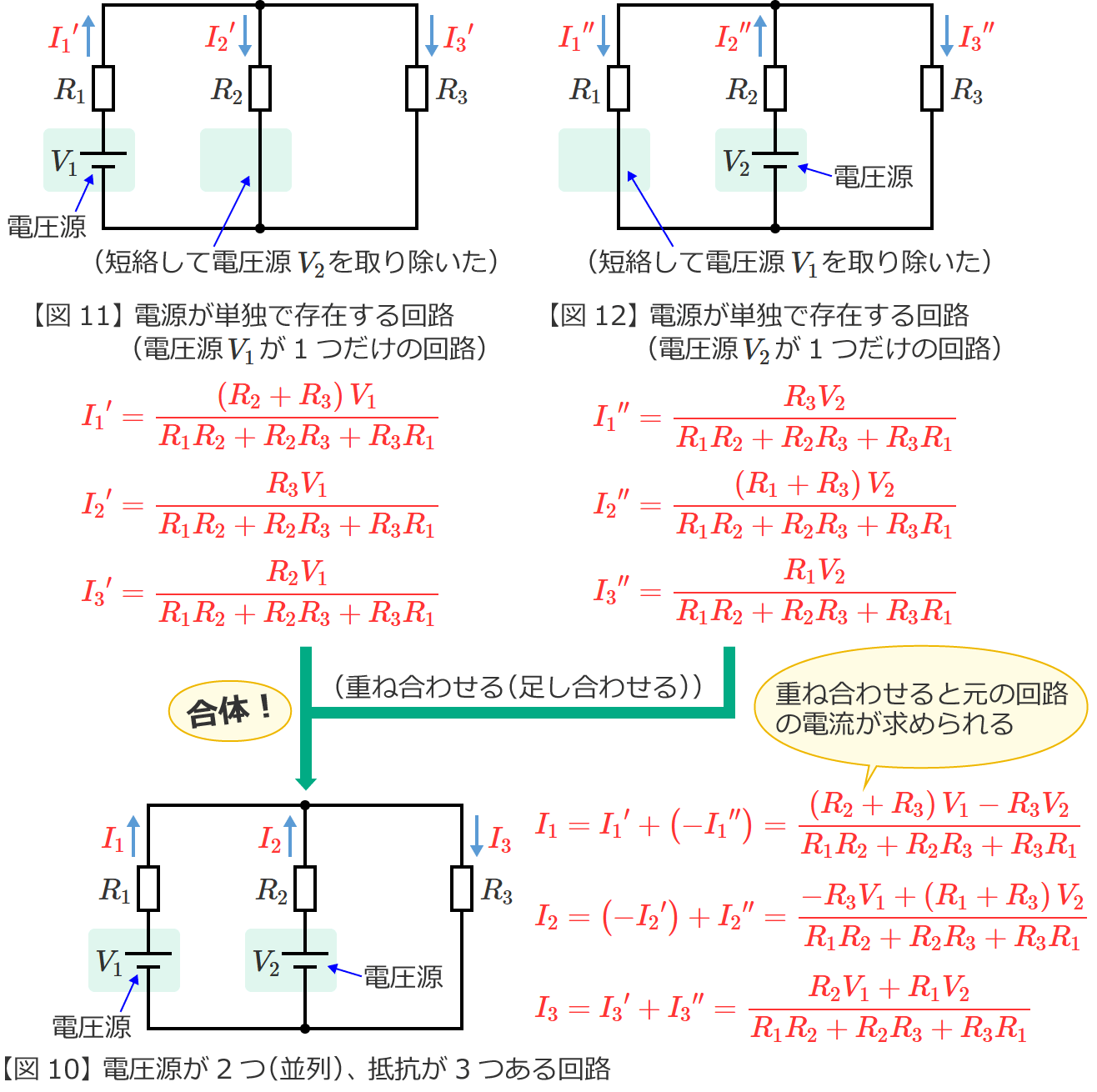
図10の回路からそれぞれの電源が単独で存在する場合の回路(図10の回路を電源ごとに分解した回路)をつくると、次の図11(電圧源 $V_1$ が単独で存在する回路)と図12(電圧源 $V_2$ が単独で存在する回路)のようになります。
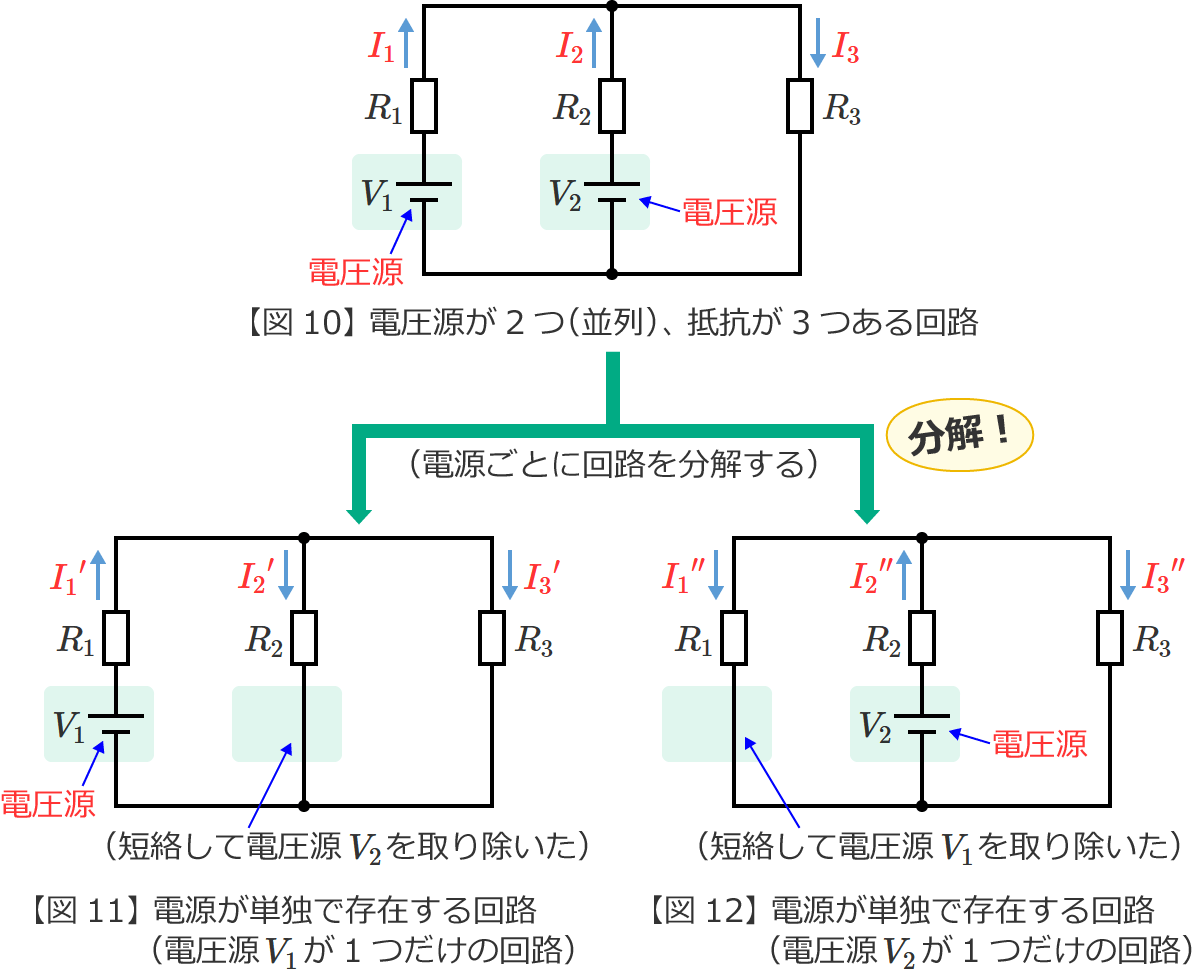
ここで、図11の電流 ${I_2}^\prime$ と図10の電流 $I_2$ の向き、図12の電流 ${I_1}^{\prime\prime}$ と図10の電流 $I_1$ の向きは反対になっていることに注意してください。
初めに、図11の回路の電流 ${I_1}^\prime$ 、${I_2}^\prime$ 、${I_3}^\prime$ を求めます。
図11の回路の合成抵抗 ${R}^\prime$ は、
${R}^\prime =R_1+\dfrac{R_2R_3}{R_2+R_3}$
$=\dfrac{R_1R_2+R_1R_3+R_2R_3}{R_2+R_3}$
$\therefore {R}^\prime =\dfrac{R_1R_2+R_2R_3+R_3R_1}{R_2+R_3}$ (図11の回路の合成抵抗 ${R}^\prime$ )
となるので、電流 ${I_1}^\prime$ は、
${I_1}^\prime =\dfrac{V_1}{{R}^\prime} =\dfrac{V_1}{\dfrac{R_1R_2+R_2R_3+R_3R_1}{R_2+R_3}}$
$\therefore {I_1}^\prime =\dfrac{\left( R_2+R_3\right) V_1}{R_1R_2+R_2R_3+R_3R_1}$ (図11の回路の電流 ${I_1}^\prime$ )
となります。また、電流 ${I_2}^\prime$ と電流 ${I_3}^\prime$ は、電流 ${I_1}^\prime$ が抵抗 $R_2$ と抵抗 $R_3$ に分流した電流なので、分流の公式より電流 ${I_2}^\prime$ と電流 ${I_3}^\prime$ は、
${I_2}^\prime ={I_1}^\prime\times\dfrac{R_3}{R_2+R_3}$ (分流の公式より)
$=\dfrac{\left( R_2+R_3\right) V_1}{R_1R_2+R_2R_3+R_3R_1}$$\times\dfrac{R_3}{R_2+R_3}$
$=\dfrac{R_3V_1}{R_1R_2+R_2R_3+R_3R_1}$
$\therefore {I_2}^\prime =\dfrac{R_3V_1}{R_1R_2+R_2R_3+R_3R_1}$ (図11の回路の電流 ${I_2}^\prime$ )
${I_3}^\prime ={I_1}^\prime\times\dfrac{R_2}{R_2+R_3}$ (分流の公式より)
$=\dfrac{\left( R_2+R_3\right) V_1}{R_1R_2+R_2R_3+R_3R_1}$$\times\dfrac{R_2}{R_2+R_3}$
$=\dfrac{R_2V_1}{R_1R_2+R_2R_3+R_3R_1}$
$\therefore {I_3}^\prime =\dfrac{R_2V_1}{R_1R_2+R_2R_3+R_3R_1}$ (図11の回路の電流 ${I_3}^\prime$ )
となります。
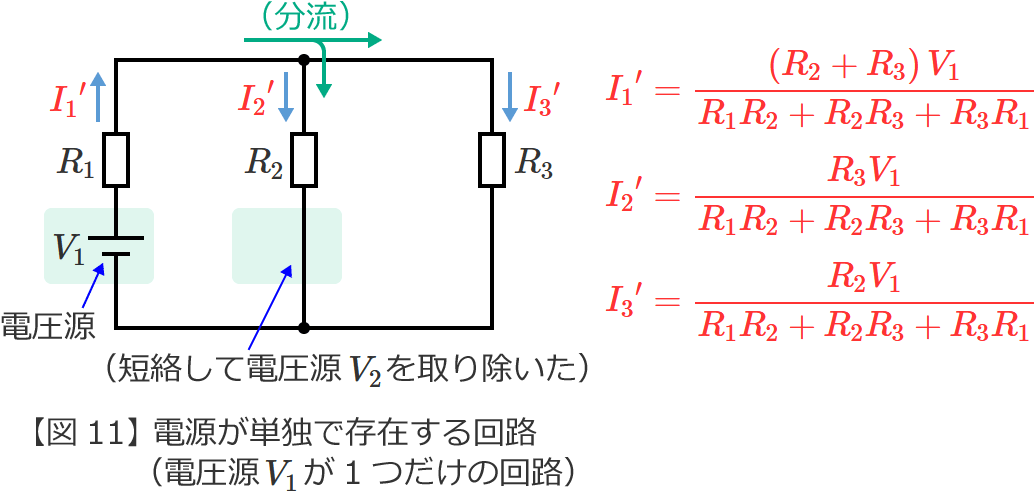
同じようにして、次に、図12の回路の電流 ${I_1}^{\prime\prime}$ 、${I_2}^{\prime\prime}$ 、${I_3}^{\prime\prime}$ を求めます。
図12の回路の合成抵抗 ${R}^{\prime\prime}$ は、
${R}^{\prime\prime} =R_2+\dfrac{R_1R_3}{R_1+R_3}$
$=\dfrac{R_2R_1+R_2R_3+R_1R_3}{R_1+R_3}$
$\therefore {R}^{\prime\prime} =\dfrac{R_1R_2+R_2R_3+R_3R_1}{R_1+R_3}$ (図12の回路の合成抵抗 ${R}^{\prime\prime}$ )
となるので、
ちょっと分かりにくいですが、図12の回路は、「抵抗 $R_2$ 」に「抵抗 $R_1$ と抵抗 $R_3$ の並列接続」が直列に接続された回路になっています。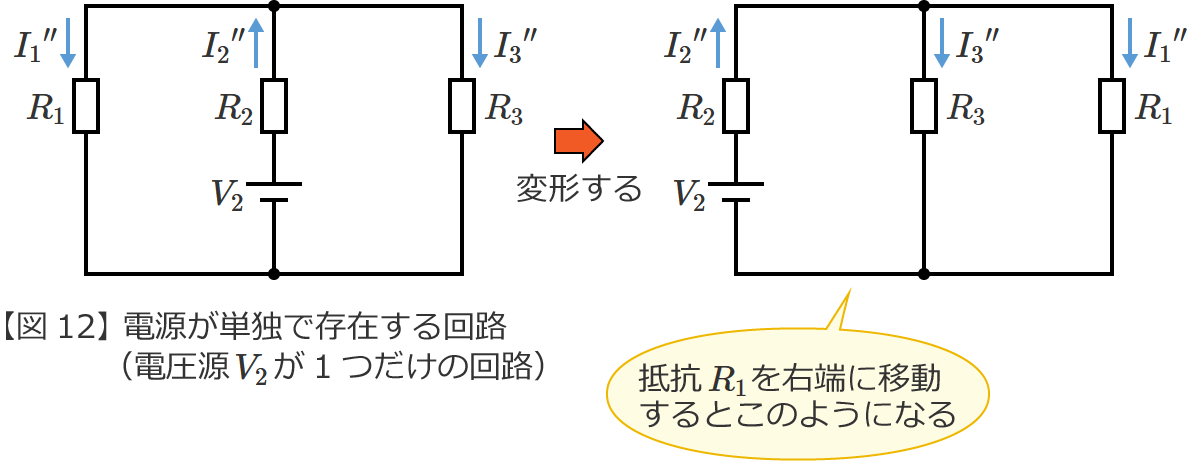
電流 ${I_2}^{\prime\prime}$ は、
${I_2}^{\prime\prime} =\dfrac{V_2}{{R}^{\prime\prime}} =\dfrac{V_2}{\dfrac{R_1R_2+R_2R_3+R_3R_1}{R_1+R_3}}$
$\therefore {I_2}^{\prime\prime} =\dfrac{\left( R_1+R_3\right) V_2}{R_1R_2+R_2R_3+R_3R_1}$ (図12の回路の電流 ${I_2}^{\prime\prime}$ )
となります。また、電流 ${I_1}^{\prime\prime}$ と電流 ${I_3}^{\prime\prime}$ は、電流 ${I_2}^{\prime\prime}$ が抵抗 $R_1$ と抵抗 $R_3$ に分流した電流なので、分流の公式より電流 ${I_1}^{\prime\prime}$ と電流 ${I_3}^{\prime\prime}$ は、
${I_1}^{\prime\prime} ={I_2}^{\prime\prime}\times\dfrac{R_3}{R_1+R_3}$ (分流の公式より)
$=\dfrac{\left( R_1+R_3\right) V_2}{R_1R_2+R_2R_3+R_3R_1}$$\times\dfrac{R_3}{R_1+R_3}$
$=\dfrac{R_3V_2}{R_1R_2+R_2R_3+R_3R_1}$
$\therefore {I_1}^{\prime\prime} =\dfrac{R_3V_2}{R_1R_2+R_2R_3+R_3R_1}$ (図12の回路の電流 ${I_1}^{\prime\prime}$ )
${I_3}^{\prime\prime} ={I_2}^{\prime\prime}\times\dfrac{R_1}{R_1+R_3}$ (分流の公式より)
$=\dfrac{\left( R_1+R_3\right) V_2}{R_1R_2+R_2R_3+R_3R_1}$$\times\dfrac{R_1}{R_1+R_3}$
$=\dfrac{R_1V_2}{R_1R_2+R_2R_3+R_3R_1}$
$\therefore {I_3}^{\prime\prime} =\dfrac{R_1V_2}{R_1R_2+R_2R_3+R_3R_1}$ (図12の回路の電流 ${I_3}^{\prime\prime}$ )
となります。
求める電流は3つ( $I_1$ 、$I_2$ 、$I_3$ )あるので、電流 $I_1$ から求めてみます。
電流 $I_1$
STEP2で求めた電流 ${I_1}^\prime$ は ${I_1}^\prime =\dfrac{\left( R_2+R_3\right) V_1}{R_1R_2+R_2R_3+R_3R_1}$ 、電流 ${I_1}^{\prime\prime}$ は ${I_1}^{\prime\prime} =\dfrac{R_3V_2}{R_1R_2+R_2R_3+R_3R_1}$ でしたので、これらを重ね合わせて(足し合わせて)元の回路(図10)の抵抗 $R_1$ に流れる電流 $I_1$ を求めると、
$I_1={I_1}^\prime +\left( -{I_1}^{\prime\prime}\right)$ …① (電流 ${I_1}^\prime$ と ${I_1}^{\prime\prime}$ を重ね合わせた)
$=\dfrac{\left( R_2+R_3\right) V_1}{R_1R_2+R_2R_3+R_3R_1}$$-\dfrac{R_3V_2}{R_1R_2+R_2R_3+R_3R_1}$
$=\dfrac{\left( R_2+R_3\right) V_1-R_3V_2}{R_1R_2+R_2R_3+R_3R_1}$
$\therefore I_1=\dfrac{\left( R_2+R_3\right) V_1-R_3V_2}{R_1R_2+R_2R_3+R_3R_1}$ (図10の回路の電流 $I_1$ )
となります。
電流 ${I_1}^{\prime\prime}$ の向きは電流 $I_1$ と逆向きなので、①式では電流 ${I_1}^{\prime\prime}$ をマイナスにして足し合わせています。
電流 $I_2$
STEP2で求めた電流 ${I_2}^\prime$ は ${I_2}^\prime =\dfrac{R_3V_1}{R_1R_2+R_2R_3+R_3R_1}$ 、電流 ${I_2}^{\prime\prime}$ は ${I_2}^{\prime\prime} =\dfrac{\left( R_1+R_3\right) V_2}{R_1R_2+R_2R_3+R_3R_1}$ でしたので、これらを重ね合わせて(足し合わせて)元の回路(図10)の抵抗 $R_2$ に流れる電流 $I_2$ を求めると、
$I_2=\left( -{I_2}^\prime \right) +{I_2}^{\prime\prime}$ …② (電流 ${I_2}^\prime$ と ${I_2}^{\prime\prime}$ を重ね合わせた)
$=\dfrac{-R_3V_1}{R_1R_2+R_2R_3+R_3R_1}$$+\dfrac{\left( R_1+R_3\right) V_2}{R_1R_2+R_2R_3+R_3R_1}$
$=\dfrac{-R_3V_1+\left( R_1+R_3\right) V_2}{R_1R_2+R_2R_3+R_3R_1}$
$\therefore I_2=\dfrac{-R_3V_1+\left( R_1+R_3\right) V_2}{R_1R_2+R_2R_3+R_3R_1}$ (図10の回路の電流 $I_2$ )
となります。
電流 ${I_2}^\prime$ の向きは電流 $I_2$ と逆向きなので、②式では電流 ${I_2}^\prime$ をマイナスにして足し合わせています。
電流 $I_3$
STEP2で求めた電流 ${I_3}^\prime$ は ${I_3}^\prime =\dfrac{R_2V_1}{R_1R_2+R_2R_3+R_3R_1}$ 、電流 ${I_3}^{\prime\prime}$ は ${I_3}^{\prime\prime} =\dfrac{R_1V_2}{R_1R_2+R_2R_3+R_3R_1}$ でしたので、これらを重ね合わせて(足し合わせて)元の回路(図10)の抵抗 $R_3$ に流れる電流 $I_3$ を求めると、
$I_3={I_3}^\prime +{I_3}^{\prime\prime}$ (電流 ${I_3}^\prime$ と ${I_3}^{\prime\prime}$ を重ね合わせた)
$=\dfrac{R_2V_1}{R_1R_2+R_2R_3+R_3R_1}$$+\dfrac{R_1V_2}{R_1R_2+R_2R_3+R_3R_1}$
$=\dfrac{R_2V_1+R_1V_2}{R_1R_2+R_2R_3+R_3R_1}$
$\therefore I_3=\dfrac{R_2V_1+R_1V_2}{R_1R_2+R_2R_3+R_3R_1}$ (図10の回路の電流 $I_3$ )
となります。
以上で、「電圧源が2つ(並列)、抵抗が3つある回路」(図10)の抵抗 $R_1$ 、$R_2$ 、$R_3$ に流れる電流 $I_1$ 、$I_2$ 、$I_3$ が求められました。
次は、「電圧源と電流源が混在している回路」の計算です。
電圧源と電流源が混在している回路
重ね合わせの理を用いて、次の回路の抵抗 $R_1$[$\Omega$]に流れる電流 $I_1$[$\mathrm{A}$]、抵抗 $R_2$[$\Omega$]に流れる電流 $I_2$[$\mathrm{A}$]、抵抗 $R_3$[$\Omega$]に流れる電流 $I_3$[$\mathrm{A}$]を求めてみます。
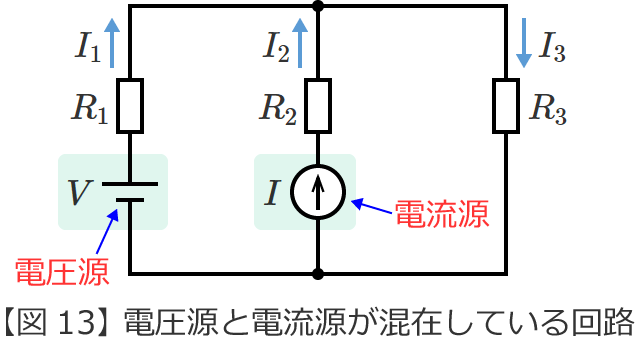
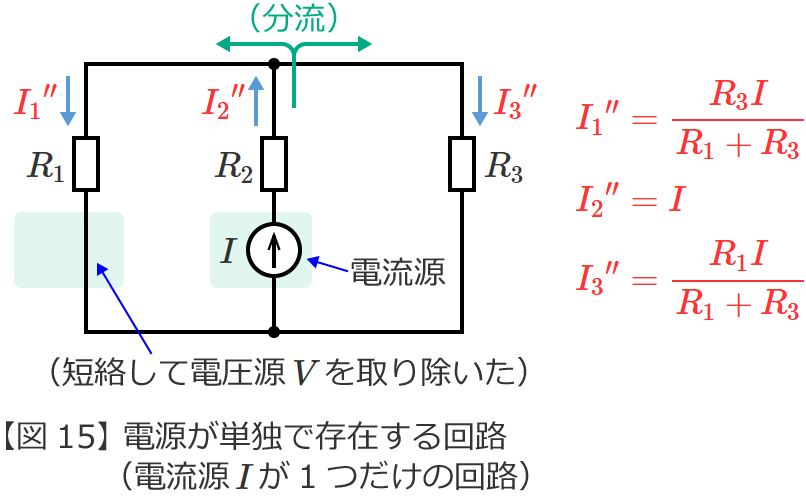
図13の回路からそれぞれの電源が単独で存在する場合の回路(図13の回路を電源ごとに分解した回路)をつくると、次の図14(電圧源 $V$ が単独で存在する回路)と図15(電流源 $I$ が単独で存在する回路)のようになります。
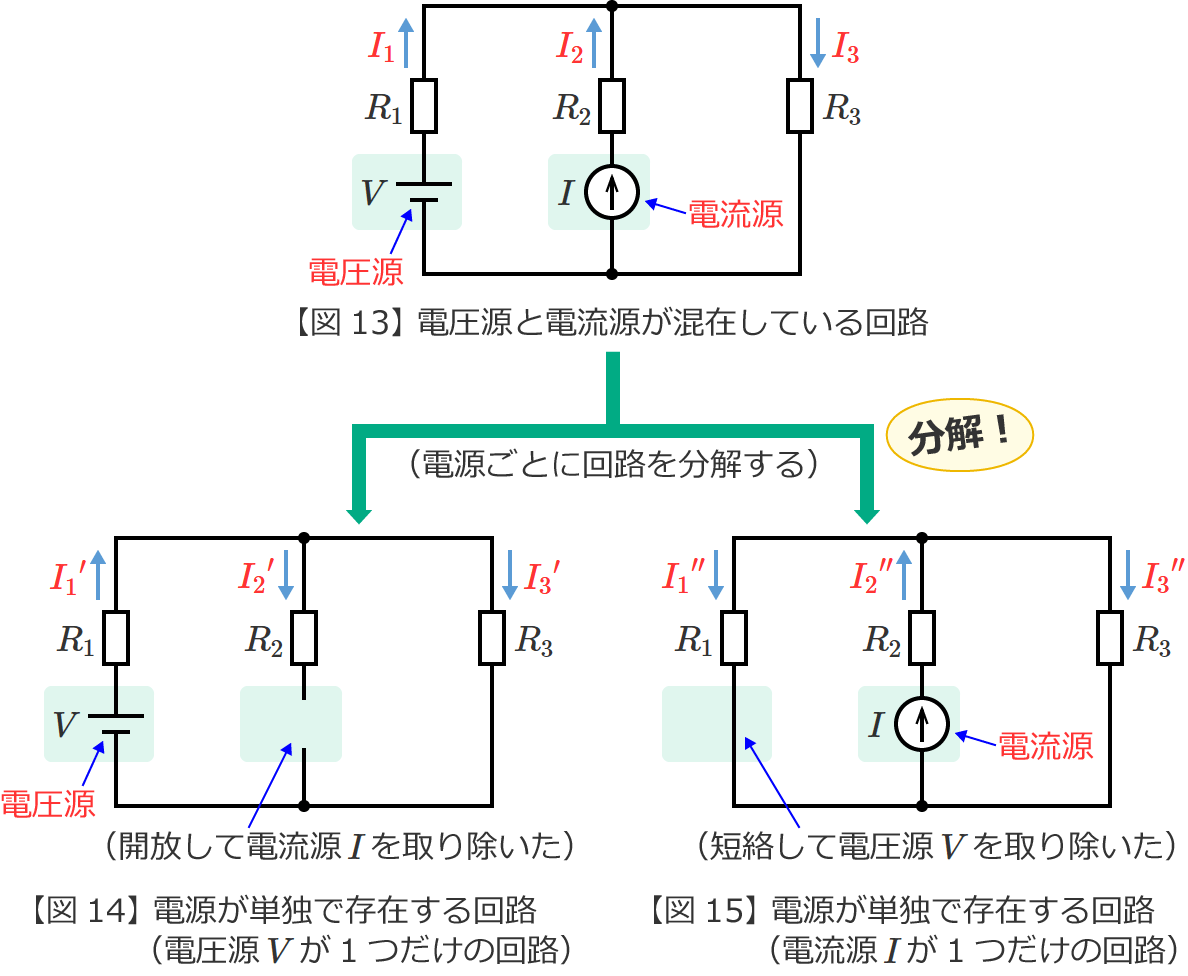
ここで、図15の電流 ${I_1}^{\prime\prime}$ と図13の電流 $I_1$ の向きは反対になっていることに注意してください。
初めに、図14の回路の電流 ${I_1}^\prime$ 、${I_2}^\prime$ 、${I_3}^\prime$ を求めます。
図14の回路の合成抵抗 ${R}^\prime$ は、
${R}^\prime =R_1+R_3$ (図14の回路の合成抵抗 ${R}^\prime$ )
となるので、電流 ${I_1}^\prime$ と電流 ${I_3}^\prime$ は、
$\therefore {I_1}^\prime ={I_3}^\prime =\dfrac{V}{R_1+R_3}$ (図14の回路の電流 ${I_1}^\prime$ と ${I_3}^\prime$ )
となります。また、電流 ${I_2}^\prime$ については、抵抗 $R_2$ の下側(電流源 $I$ があったところ)が開放されていることから抵抗 $R_2$ には電流が流れないので、
${I_2}^\prime =0$
となります。

次に、図15の回路の電流 ${I_1}^{\prime\prime}$ 、${I_2}^{\prime\prime}$ 、${I_3}^{\prime\prime}$ を求めます。
電流 ${I_2}^{\prime\prime}$ は、電流源 $I$ の電流と同じなので(電流源 $I$ から流れ出た電流がそのまま抵抗 $R_2$ に流れる)、
$\therefore {I_2}^{\prime\prime} =I$ (図15の回路の電流 ${I_2}^{\prime\prime}$ )
となります。また、電流 ${I_1}^{\prime\prime}$ と電流 ${I_3}^{\prime\prime}$ は、電流 ${I_2}^{\prime\prime}$ が抵抗 $R_1$ と抵抗 $R_3$ に分流した電流なので、分流の公式より電流 ${I_1}^{\prime\prime}$ と電流 ${I_3}^{\prime\prime}$ は、
${I_1}^{\prime\prime} ={I_2}^{\prime\prime}\times\dfrac{R_3}{R_1+R_3}$ (分流の公式より)
$=I\times\dfrac{R_3}{R_1+R_3}$
$=\dfrac{R_3I}{R_1+R_3}$
$\therefore {I_1}^{\prime\prime} =\dfrac{R_3I}{R_1+R_3}$ (図15の回路の電流 ${I_1}^{\prime\prime}$ )
${I_3}^{\prime\prime} ={I_2}^{\prime\prime}\times\dfrac{R_1}{R_1+R_3}$ (分流の公式より)
$=I\times\dfrac{R_1}{R_1+R_3}$
$=\dfrac{R_1I}{R_1+R_3}$
$\therefore {I_3}^{\prime\prime} =\dfrac{R_1I}{R_1+R_3}$ (図15の回路の電流 ${I_3}^{\prime\prime}$ )
となります。
求める電流は3つ( $I_1$ 、$I_2$ 、$I_3$ )あるので、電流 $I_1$ から求めてみます。
電流 $I_1$
STEP2で求めた電流 ${I_1}^\prime$ は ${I_1}^\prime =\dfrac{V}{R_1+R_3}$ 、電流 ${I_1}^{\prime\prime}$ は ${I_1}^{\prime\prime} =\dfrac{R_3I}{R_1+R_3}$ でしたので、これらを重ね合わせて(足し合わせて)元の回路(図13)の抵抗 $R_1$ に流れる電流 $I_1$ を求めると、
$I_1={I_1}^\prime +\left( -{I_1}^{\prime\prime}\right)$ …③ (電流 ${I_1}^\prime$ と ${I_1}^{\prime\prime}$ を重ね合わせた)
$=\dfrac{V}{R_1+R_3} -\dfrac{R_3I}{R_1+R_3}$
$=\dfrac{V-R_3I}{R_1+R_3}$
$\therefore I_1=\dfrac{V-R_3I}{R_1+R_3}$ (図13の回路の電流 $I_1$ )
となります。
電流 ${I_1}^{\prime\prime}$ の向きは電流 $I_1$ と逆向きなので、③式では電流 ${I_1}^{\prime\prime}$ をマイナスにして足し合わせています。
電流 $I_2$
STEP2で求めた電流 ${I_2}^\prime$ は ${I_2}^\prime =0$ 、電流 ${I_2}^{\prime\prime}$ は ${I_2}^{\prime\prime} =I$ でしたので、これらを重ね合わせて(足し合わせて)元の回路(図13)の抵抗 $R_2$ に流れる電流 $I_2$ を求めると、
$I_2=\left( -{I_2}^\prime\right) +{I_2}^{\prime\prime}$ …④ (電流 ${I_2}^\prime$ と ${I_2}^{\prime\prime}$ を重ね合わせた)
$=-0+I$
$=I$
$\therefore I_2=I$ (図13の回路の電流 $I_2$ )
となります。
電流 ${I_2}^\prime$ の向きは電流 $I_2$ と逆向きなので、④式では電流 ${I_2}^\prime$ をマイナスにして足し合わせています。(といっても、電流 ${I_2}^\prime$ はゼロなんですけどね。)
電流 $I_3$
STEP2で求めた電流 ${I_3}^\prime$ は ${I_3}^\prime =\dfrac{V}{R_1+R_3}$ 、電流 ${I_3}^{\prime\prime}$ は ${I_3}^{\prime\prime} =\dfrac{R_1I}{R_1+R_3}$ でしたので、これらを重ね合わせて(足し合わせて)元の回路(図13)の抵抗 $R_3$ に流れる電流 $I_3$ を求めると、
$I_3={I_3}^\prime +{I_3}^{\prime\prime}$ (電流 ${I_3}^\prime$ と ${I_3}^{\prime\prime}$ を重ね合わせた)
$=\dfrac{V}{R_1+R_3} +\dfrac{R_1I}{R_1+R_3}$
$=\dfrac{V+R_1I}{R_1+R_3}$
$\therefore I_3=\dfrac{V+R_1I}{R_1+R_3}$ (図13の回路の電流 $I_3$ )
となります。
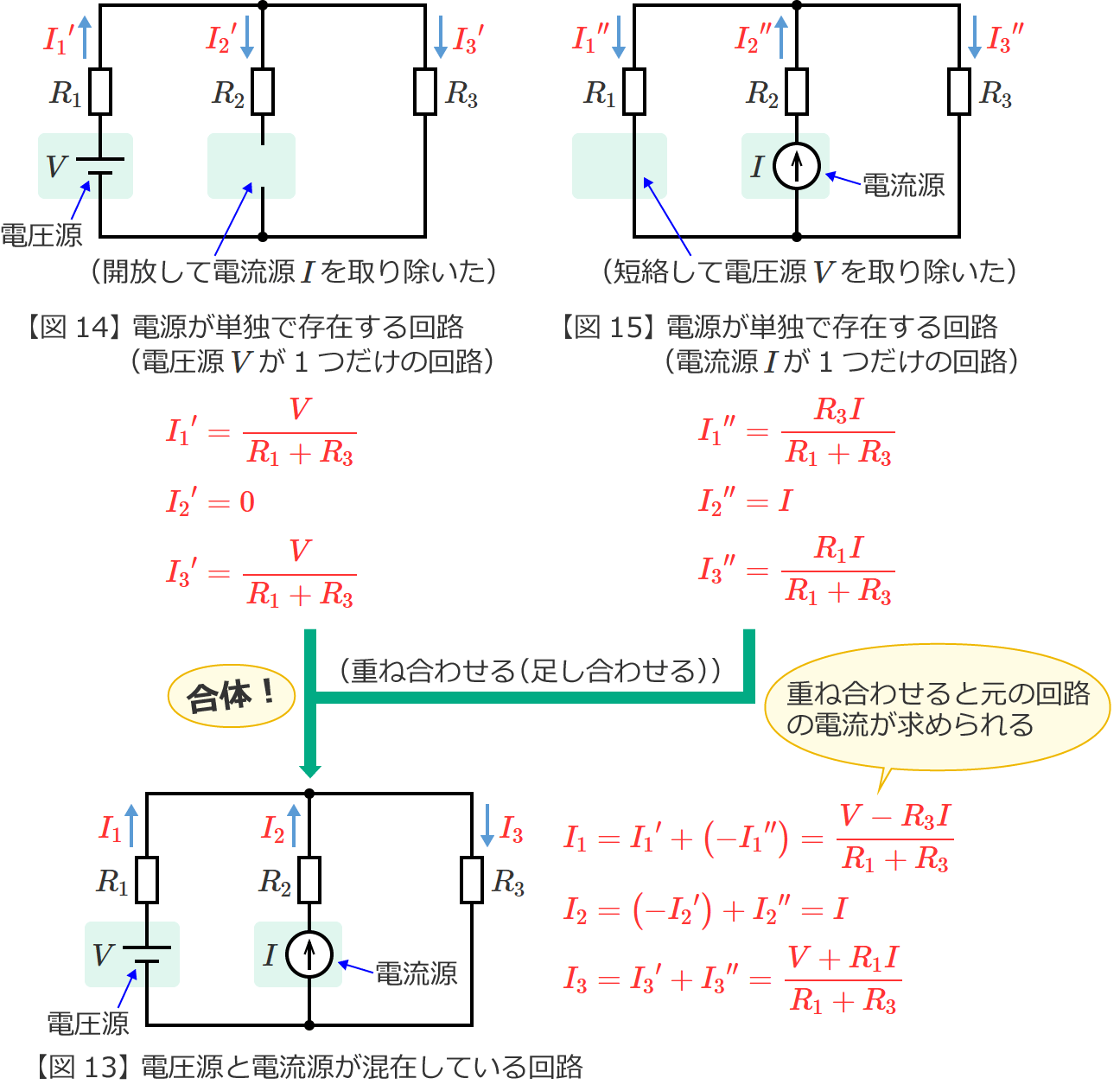
以上で、「電圧源と電流源が混在している回路」(図13)の抵抗 $R_1$ 、$R_2$ 、$R_3$ に流れる電流 $I_1$ 、$I_2$ 、$I_3$ が求められました。
重ね合わせの理はおぼえておくとなにかと役に立つ定理ですので、重ね合わせの理の使い方はおぼえておくようにしましょう!
- 重ね合わせの理は、「電源を複数含む回路の任意の部分の電流(または電圧)は、複数の電源それぞれを単独で存在させた場合の電流(または電圧)を重ね合わせたもの(足し合わせたもの)に等しい」という定理。
- 重ね合わせの理を使って電流(または電圧)を求めるときの手順は、以下のようになる。
❶元の回路を電源ごとに分解する(電圧源を取り除くときは短絡、電流源を取り除くときは開放する)
❷❶で分解した回路それぞれにおける電流(または電圧)を求める
❸❷で求めた電流(または電圧)を重ね合わせて元の回路の電流(または電圧)を求める
スポンサーリンク
スポンサーリンク
短絡されている抵抗がある場合の合成抵抗の求め方 ←BACK
NEXT→ テブナンの定理
スポンサーリンク
重ね合わせの理 関連ページ
- 合成抵抗の求め方(計算方法)
- 合成抵抗の計算は直流回路、交流回路の計算をするときの基本になります。合成抵抗の計算は複雑そうに思えますが、基本的には、抵抗が2個の場合の直列接続または並列接続の合成抵抗の求め方さえ分かっていれば、ほとんどの回路の合成抵抗を求めることができます。
- 短絡されている抵抗がある場合の合成抵抗の求め方
- 短絡されている抵抗がある場合の合成抵抗の求め方について解説しています。回路に短絡されている抵抗があるんだけど、どうやって合成抵抗を求めるの?なんてときに参考にしてみてください。
- テブナンの定理
- テブナンの定理(鳳-テブナンの定理)について解説しています。テブナンの定理は等価電圧源の定理とも呼ばれ、回路の特定の素子に流れる電流を求めるときに有用な定理です。テブナンの定理を使った回路の計算方法や、テブナンの定理の証明についても解説していますので参考にしてみてください。
- ノートンの定理
- ノートンの定理について解説しています。ノートンの定理は等価電流源の定理とも呼ばれ、回路の特定の素子にかかる電圧を求めるときに有用な定理です。ノートンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。
- ミルマンの定理
- ミルマンの定理について解説しています。ミルマンの定理は全電圧の定理とも呼ばれ、抵抗と電源の直列接続が複数並列に接続されている回路の端子電圧を求めたいときに有用な定理です。ミルマンの定理の式の導出方法や、ミルマンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。
- 分圧の法則による直流回路の計算
- 分圧の法則を使った直流回路の計算方法の例です。分圧の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。
- 分流の法則による直流回路の計算
- 分流の法則を使った直流回路の計算方法の例です。分流の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。
- ループ解析(基本)
- 直流回路の計算をするときによく使われる「ループ解析」の方法と基本的な手順について解説しています。ループ解析はキルヒホッフの第二法則(電圧則)を応用した電気回路の計算方法です。
- 電圧源と電流源の等価変換
- 電圧源と電流源の等価変換について解説しています。電圧源と電流源が等価になるための条件や、電圧源から電流源、電流源から電圧源への等価変換のやり方などについて解説していますので参考にしてみてください。
- 電源から供給できる最大電力(最大有能電力)
- 電源から供給できる最大電力(最大有能電力)について解説しています。内部抵抗をもつ電源は、負荷に供給できる電力に上限(限界)があります。電源からの供給電力が最大になるための条件や、負荷に供給できる電源の最大電力(最大有能電力)などについて解説していますので、参考にしてみてください。
- コンデンサの静電容量と電荷の計算の基本(直列接続と並列接続)
- コンデンサの静電容量と電荷の計算の基本についてまとめています。コンデンサの計算は、コンデンサ2個を直列接続または並列接続したときの考え方と計算方法が基本になります。
- 合成静電容量の求め方(計算方法)
- 合成静電容量の計算は直流回路、交流回路の計算をするときの基本になります。合成静電容量の計算は複雑そうに思えますが、基本的には、コンデンサが2個の場合の直列接続または並列接続の合成静電容量の求め方さえ分かっていれば、ほとんどの回路の合成静電容量を求めることができます。
- ジュール熱とジュールの法則
- 抵抗や金属などの導体に電流が流れたときに発生するジュール熱と、ジュールの法則について解説しています。ジュール熱が発生する理由(原理)についても解説していますので、ジュール熱・ジュールの法則の勉強の参考にしてみてください。


