スポンサーリンク
電界中の電子の運動
※ページ内にPR・広告が含まれる場合があります。
電界中にある電子は電界から力(静電力)を受けるので、電界の中に電子を置くと電子は動き出します。
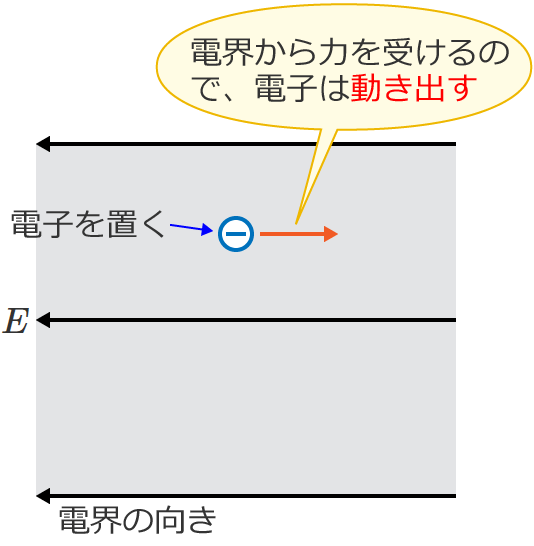
電界のことを電場ともいいます。
また、次の図のように電界に電子が突入すると、電界の中では電子は電界から力を受けるので、電界の中を進む電子の方向は曲がります。

このように、電子は電界から力を受けるので、電界の中に電子を置くと電子は動き出し、また、電界に電子が突入するとその進む方向が変わったりします。
電界の中にある電子は常に電界から力を受けるので、電界中の電子はじっとその場に留まることはなく、動いてしまうんです。つまり、電界中にある電子は、何かしらの運動をする(動く)ことになります。
では、電界中の電子はどのような運動をするのでしょうか?
スポンサーリンク
電界中に電子を置いたときの電子の運動
まず初めに、電界中に電子を置いたときの電子の運動について考えてみましょう。
電子の電荷を $-e$[$\mathrm{C}$]、電界の強さを $E$[$\mathrm{V/m}$]とすると、電界 $E$ の中にある電子は、電界の向きと反対向きに $F=eE$[$\mathrm{N}$]の大きさの力を受けます。
なので、例えば、次の図のように電界の強さが $E$[$\mathrm{V/m}$]の一様な電界中に電子を置いてみると、
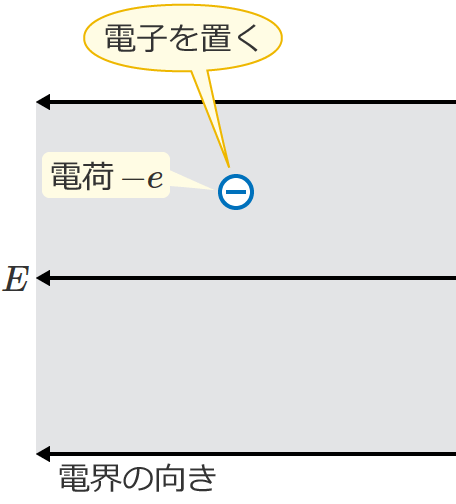
電子は電界の向きと反対向きに $F=eE$[$\mathrm{N}$]の力を受けるので、電子は電界の向きと反対方向に動き出します。
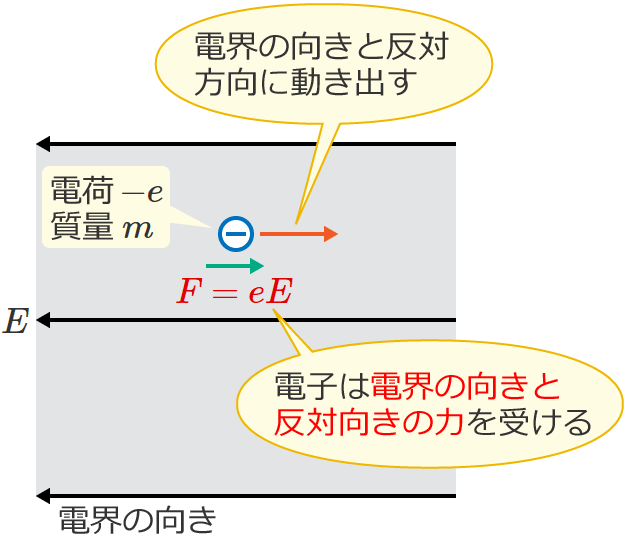
このとき、電子は $F=eE$[$\mathrm{N}$]の一定の大きさの力を受けて動くので、電子の質量を $m$[$\mathrm{kg}$]、電子の加速度を $a$[$\mathrm{m/s^2}$]とすると、電子の運動方程式は、
$ma=eE$ …①
となります。この①式から電子の加速度 $a$ を求めてみると、
$ma=eE$ より、
$\therefore a=\dfrac{eE}{m}$ [$\mathrm{m/s^2}$] …② (電子の加速度)
となります。ここで、この②式の右辺をみてみると、
- $e$ :電子の電荷の大きさなので $e$ は一定値
- $E$ :一様な電界 $E$ なので $E$ は一定値
- $m$ :電子の質量なので $m$ は一定値
なので、②式の電子の加速度(②式の左辺)も一定の値になります。
すなわち、一様な電界中に電子を置くと、電子は加速度が一定の等加速度運動をします。
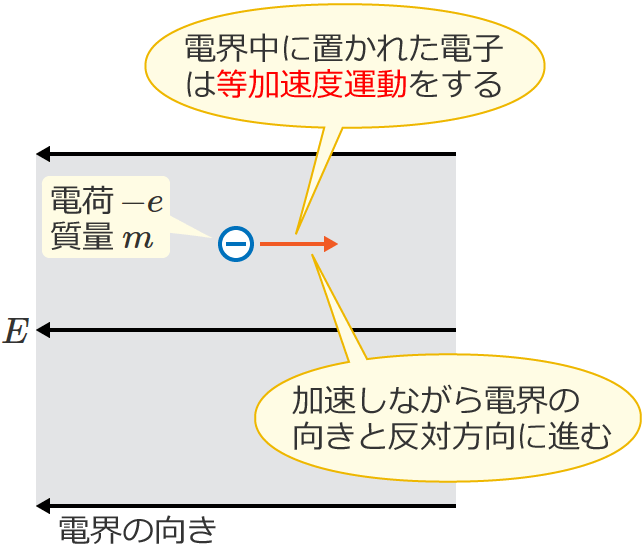
ちなみに、求めた②の電子の加速度 $a$ より、$t$ 秒後の電子の速度 $v$、電子の移動距離 $x$、電子の運動エネルギー $W$ を求めてみると以下のようになります。
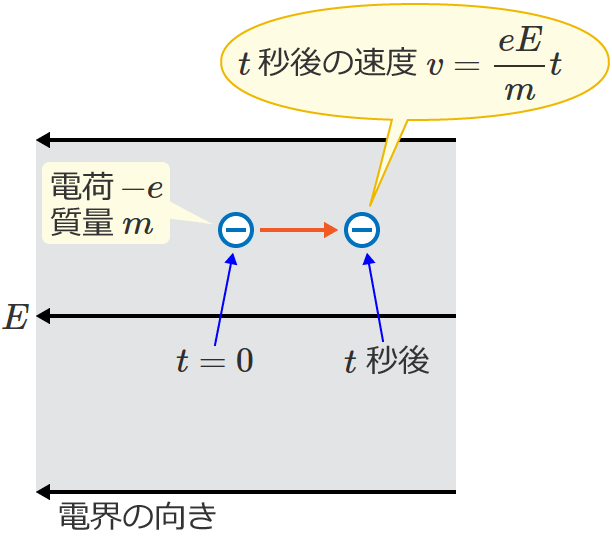
t秒後の電子の速度
初速度がゼロの場合の速度 $v$[$\mathrm{m/s}$]は、加速度を $a$[$\mathrm{m/s^2}$]、時間を $t$[$\mathrm{s}$]とすると、$v=at$ と表わされるので、$t$ 秒後の電子の速度 $v$[$\mathrm{m/s}$]は、
$v=at=\dfrac{eE}{m} t$
$\therefore v=\dfrac{eE}{m} t$ [$\mathrm{m/s}$] ($t$ 秒後の電子の速度)
になります。
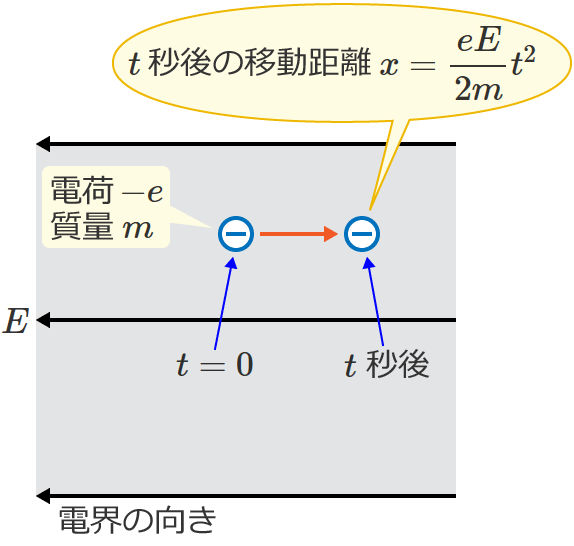
t秒後の電子の移動距離
初速度がゼロの場合の移動距離 $x$[$\mathrm{m}$]は、加速度を $a$[$\mathrm{m/s^2}$]、時間を $t$[$\mathrm{s}$]とすると、$x=\dfrac{1}{2} at^2$ と表わされるので、$t$ 秒後の電子の移動距離 $x$[$\mathrm{m}$]は、
$x=\dfrac{1}{2} at^2=\dfrac{1}{2}\left(\dfrac{eE}{m}\right) t^2=\dfrac{eE}{2m} t^2$
$\therefore x=\dfrac{eE}{2m} t^2$ [$\mathrm{m}$] ($t$ 秒後の電子の移動距離)
になります。
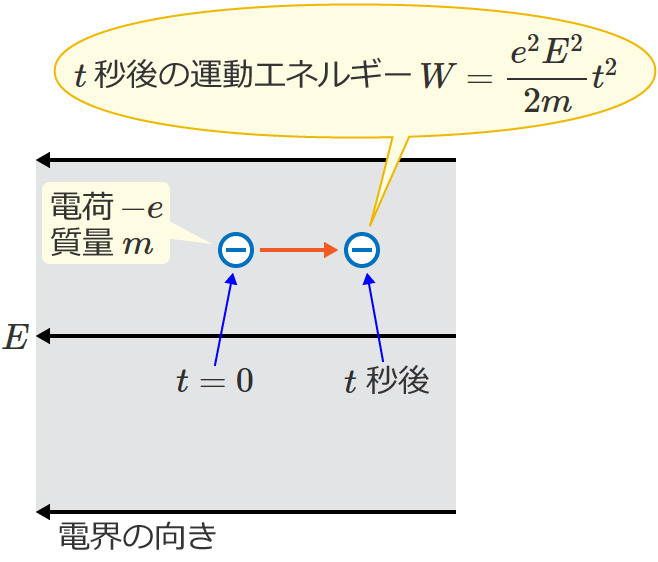
t秒後の電子の運動エネルギー
電子の運動エネルギー $W$[$\mathrm{J}$]は、電子の質量を $m$[$\mathrm{kg}$]、電子の速度を $v$[$\mathrm{m/s}$]とすると、$W=\dfrac{1}{2} mv^2$ と表わされるので、$t$ 秒後の電子の運動エネルギー $W$[$\mathrm{J}$]は、
$W=\dfrac{1}{2} mv^2=\dfrac{m}{2}\left(\dfrac{eE}{m} t\right)^2$ $=\dfrac{me^2E^2}{2m^2} t^2$ $=\dfrac{e^2E^2}{2m} t^2$
$\therefore W=\dfrac{e^2E^2}{2m} t^2$ [$\mathrm{J}$] ($t$ 秒後の電子の運動エネルギー)
になります。
以上のように、$t$ 秒後の電子の速度、移動距離、運動エネルギーは、電子の加速度さえ求めてしまえば、あとは公式にあてはめるだけで簡単に求めることができます。
スポンサーリンク
スポンサーリンク
電界に電子が突入したときの電子の運動
次は、電界に電子が斜めに突入したときの電子の運動について考えてみましょう。
次の図のように、電界の強さが $E$[$\mathrm{V/m}$]の一様な電界中に、速さ $v$[$\mathrm{m/s}$]の電子が電界の向きに対して $\theta$( $0\lt\theta\lt 90^\circ$ )の角度で突入したとします。
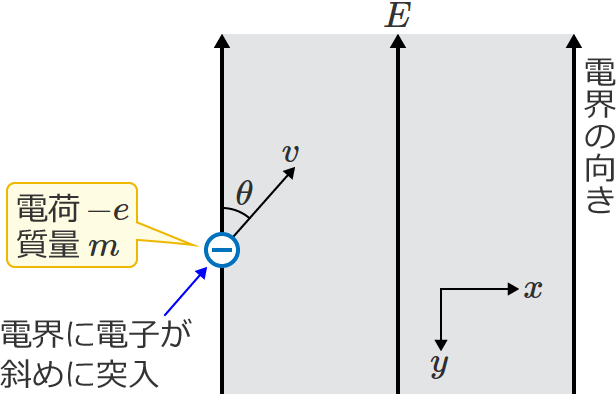
このとき電子は、電界の向きと直角の方向(図中の $x$ 方向)には力を受けませんが、電界の向きと反対向き(図中の $y$ 方向)には $F=eE$[$\mathrm{N}$]の大きさの力を受けます。
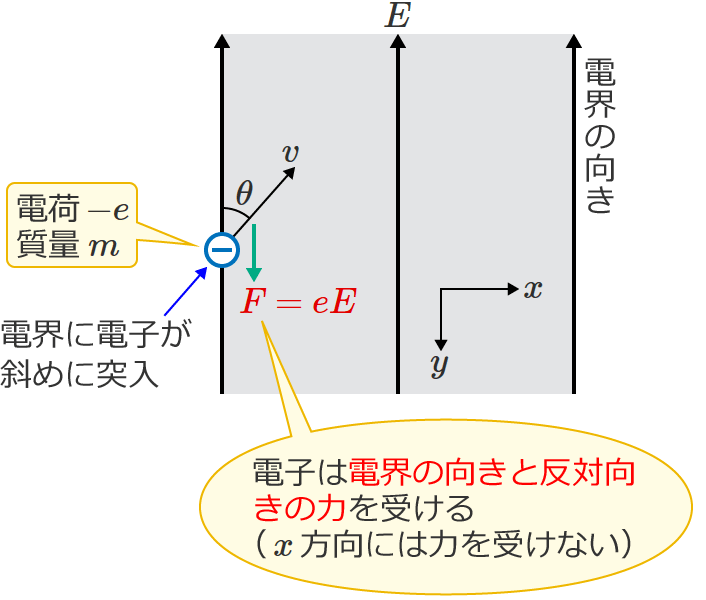
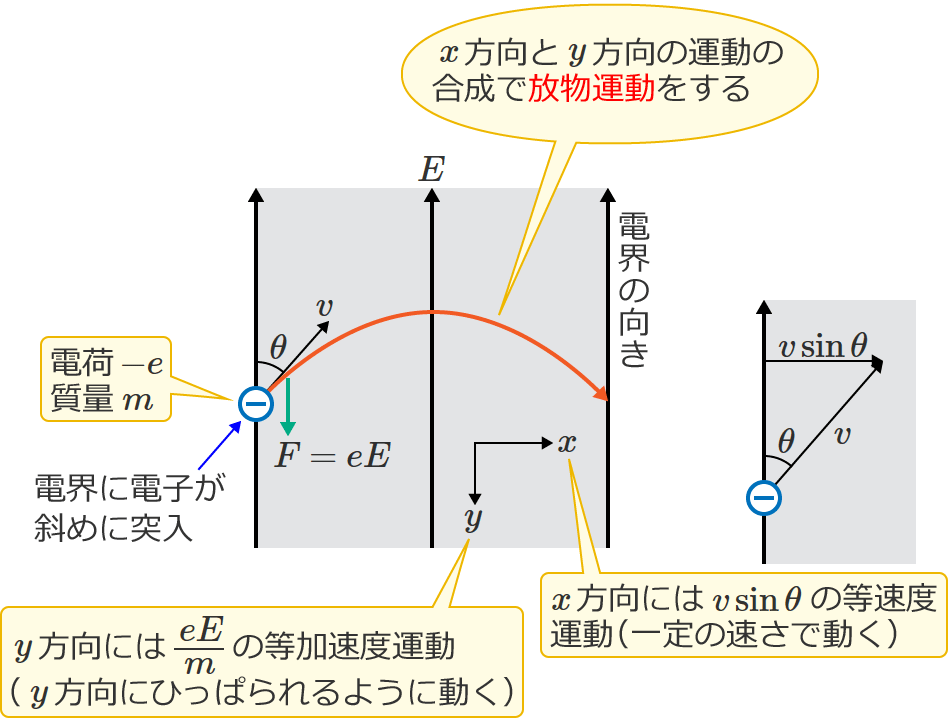
なので、$x$ 方向に対しては速度 $v\sin\theta$[$\mathrm{m/s}$]の等速度運動をし、$y$ 方向に対しては加速度 $a=\dfrac{eE}{m}$[$\mathrm{m/s^2}$]の等加速度運動をするので、電子は $x$ 方向の運動と $y$ 方向の運動を合成した次のような放物線を描く運動(放物運動)をします。(加速度 $a$ は $y$ 方向の運動方程式 $ma=eE$ より求めたものです。)
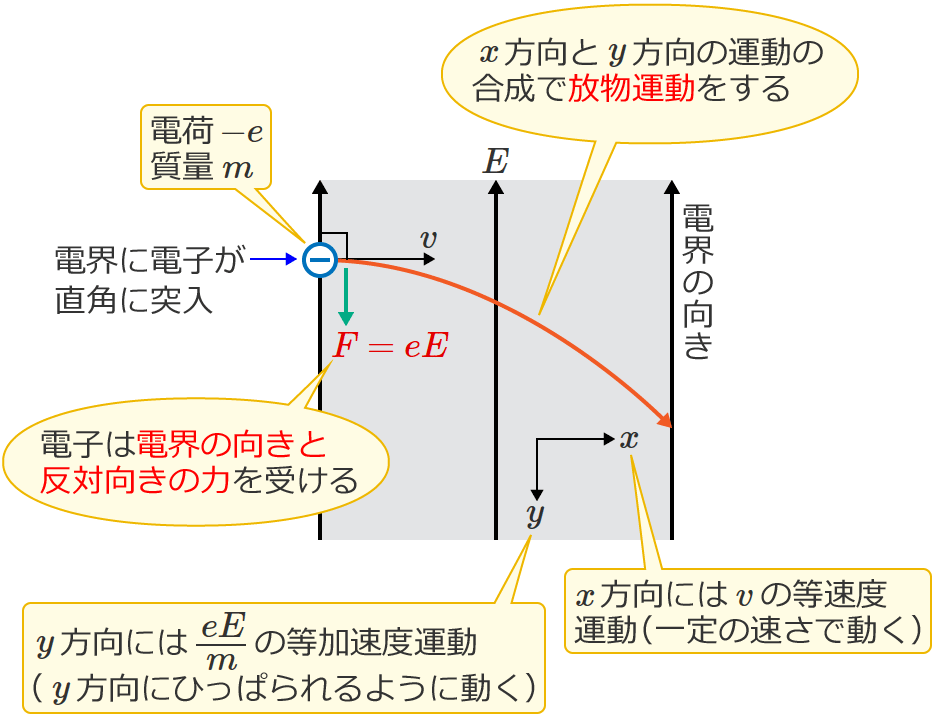
ちなみに、電界に電子が直角に突入した場合は、$x$ 方向に対しては速度 $v$[$\mathrm{m/s}$]の等速度運動をし、$y$ 方向に対しては加速度 $a=\dfrac{eE}{m}$[$\mathrm{m/s^2}$]の等加速度運動をするので、電子は次のような放物運動をします。
以上のように、電界中にある電子は電界から力(静電力)を受けるので、電界中の電子は「等加速度運動」や「放物運動」をします。
- 電界中の電子は、電界の向きと反対向きに $F=eE$[$\mathrm{N}$]の大きさの力(静電力)を受ける
- 電界中に電子を置くと、電子は等加速度運動をする
- 電子が電界の向きに対して $\theta$( $0\lt\theta\leqq 90^\circ$ )の角度で電界に突入すると、電子は放物運動をする
スポンサーリンク
スポンサーリンク
磁界中の荷電粒子の運動については、こちらのローレンツ力のページを参考にしてみてください。
電界中の電子の位置エネルギーや運動エネルギーなどについては、こちらの電界中の電子のエネルギーと電子が陽極に達したときの速度のページを参考にしてみてください。
フレミングの左手の法則と右手の法則 ←BACK
スポンサーリンク
電界中の電子の運動 関連ページ
- クーロンの法則
- 電気磁気学の「クーロンの法則」について解説しています。クーロンの法則は電気磁気学の中でも特に重要な法則で、電荷間に働く力を求めるときなどに使われます。このページではクーロンの法則をできるだけ簡単に理解できるように、電荷のイメージから解説しています。
- 右ねじの法則
- 電気磁気学の「右ねじの法則」とその使い方についてできるだけ簡単に解説しています。右ねじの法則は電流と磁界の向き(方向)の関係を表わした法則で、アンペールの右ねじの法則とか、アンペアの右ねじの法則と呼ばれたりもします。
- ビオ・サバールの法則
- 電気磁気学の「ビオ・サバールの法則」とその法則を使った磁界の計算方法について解説しています。直線状電流の磁界の計算方法や円形コイル電流の磁界の計算方法はビオ・サバールの法則の使い方の基本になりますので、おぼえておくようにしましょう。
- フレミングの左手の法則と右手の法則
- 「フレミングの左手の法則」と「フレミングの右手の法則」について解説しています。フレミングの左手の法則と右手の法則は、「電流の向き」と「磁界の向き」と「力の向き」の関係を表わした法則で、「力の向き」を求めるときはフレミングの左手の法則、「電流の向き」を求めるときはフレミングの右手の法則を使います。
- 電界中の電子のエネルギーと電子が陽極に達したときの速度
- 電界中の電子のエネルギーと電子が陽極に達したときの速度について解説しています。電界中の電子の位置エネルギーや運動エネルギーなどについて解説していますので、電界中の電子のエネルギーの勉強の参考にしてみてください。
- ローレンツ力
- ローレンツ力について解説しています。ローレンツ力の力の向きや大きさの求め方、円運動などについても解説していますので、ローレンツ力の勉強の参考にしてみてください。
- 電磁誘導
- 電気磁気学の「電磁誘導」と「電磁誘導に関するファラデーの法則」について解説しています。電磁誘導は、コイルを貫く磁束が変化するとコイルに起電力(誘導起電力)が発生する現象です。
- レンツの法則
- 電気磁気学の「レンツの法則」について解説しています。電磁誘導により発生する誘導起電力は、コイルを貫く磁束の変化を妨げるような向きに生じます。これをレンツの法則といいます。


