スポンサーリンク
電界中の電子のエネルギーと電子が陽極に達したときの速度
※ページ内にPR・広告が含まれる場合があります。
次の図のように、$V$[$\mathrm{V}$]の電圧がかけられている平行平板電極があるとします。
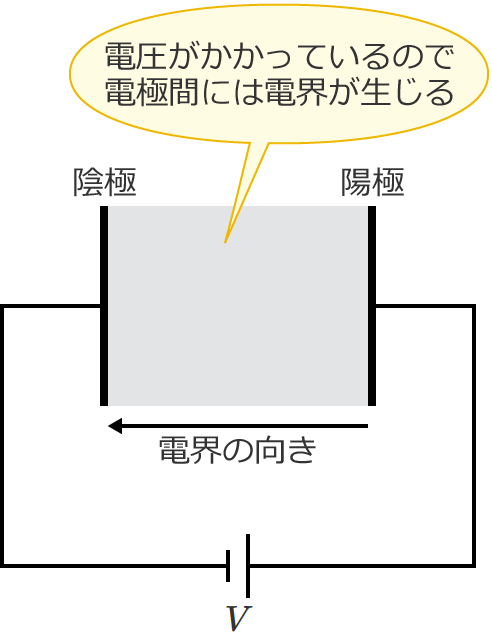
電源のプラスに接続した電極を陽極、電源のマイナスに接続した電極を陰極といいます。
この平行平板電極の陰極側に電子を1個置いてみると、
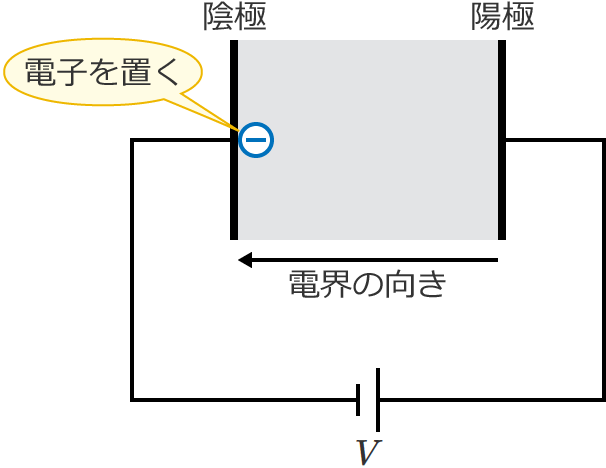
電子は電界の向きと反対向きに力(静電力)を受けるので、電子は陽極側に加速しながら進みます。
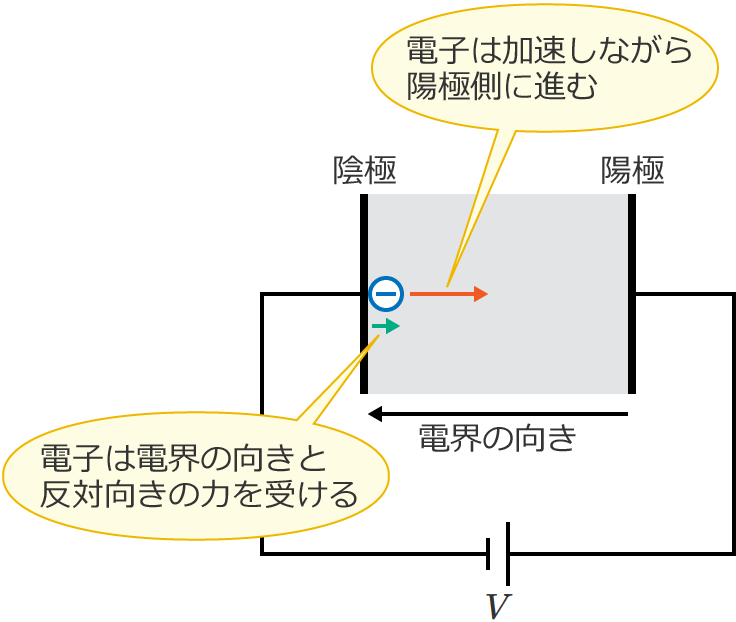
このページでは、上の図のように平行平板電極間に生じる電界中における電子のエネルギーと、電子が陽極に達したときの速度について解説します。
スポンサーリンク
電界中の電子のエネルギー
「陰極に電子を置いたときの電子のエネルギー」と「陽極に達したときの電子のエネルギー」について考えてみましょう。
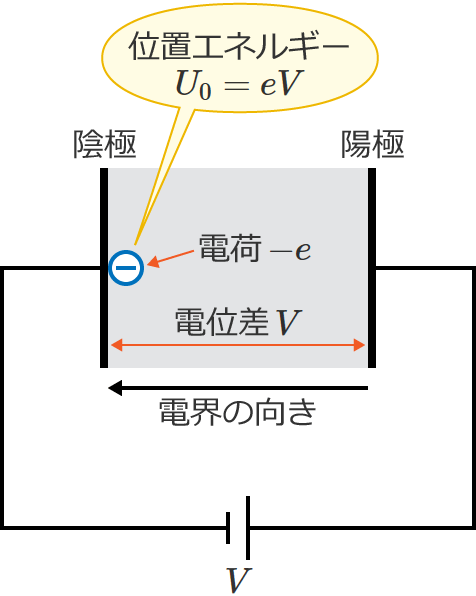
まず初めに、陰極に電子を置いたときの電子のエネルギーについて考えます。
陰極に電子を置いたときの電子の電気的な位置エネルギー $U_0$[$\mathrm{J}$]は、電子の電荷を $-e$[$\mathrm{C}$]とすると、電極間の電位差が $V$[$\mathrm{V}$]なので、
$\therefore U_0=eV$ [$\mathrm{J}$] …① (陰極に電子を置いたときの電子の位置エネルギー)
になります。
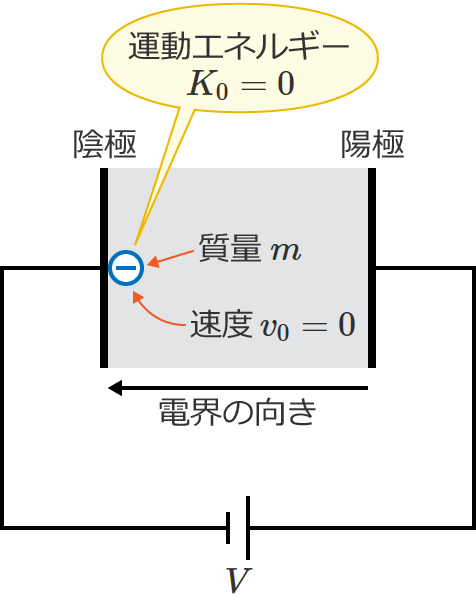
また、陰極に電子を置いた直後は電子は動いていないので(電子の速度 $v_0=0$[$\mathrm{m/s}$])、陰極に電子を置いたときの電子の運動エネルギー $K_0$[$\mathrm{J}$]は、
$K_0=\dfrac{1}{2} m{v_0}^2=\dfrac{1}{2} m\times 0^2=0$
$\therefore K_0=0$ [$\mathrm{J}$] …② (陰極に電子を置いたときの電子の運動エネルギー)
になります。( $m$ は電子の質量[$\mathrm{kg}$]です。)
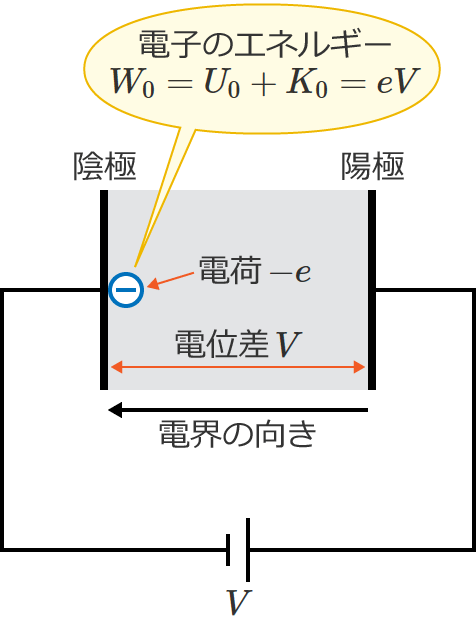
したがって、陰極に電子を置いたときの電子のエネルギー $W_0$[$\mathrm{J}$]は、①の位置エネルギーと②の運動エネルギーを足して、
$W_0=U_0+K_0=eV+0=eV$
$\therefore W_0=eV$ [$\mathrm{J}$] (陰極に電子を置いたときの電子のエネルギー)
になります。
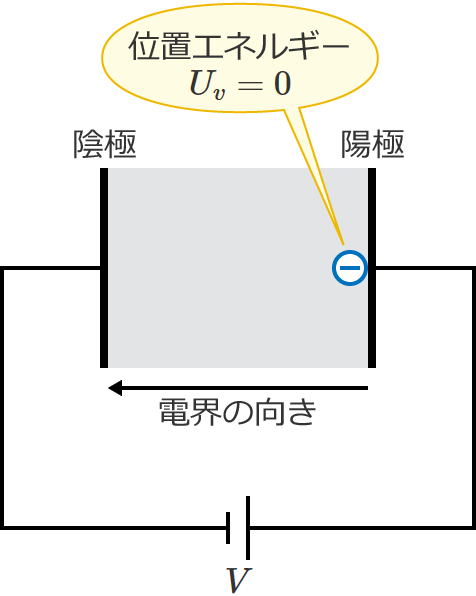
次に、陽極に達したときの電子のエネルギーについて考えます。
陽極に電子が達したときの電子の電気的な位置エネルギー $U_v$[$\mathrm{J}$]は、電位差が $0$[$\mathrm{V}$]なので、
$\therefore U_v=0$ [$\mathrm{J}$] …③ (陽極に電子が達したときの電子の位置エネルギー)
になります。
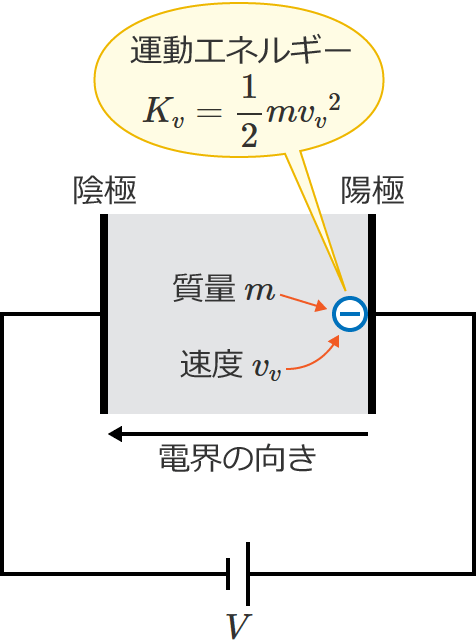
また、陽極に電子が達したときの電子の速度を $v_v$[$\mathrm{m/s}$]とすると、陽極に電子が達したときの電子の運動エネルギー $K_v$[$\mathrm{J}$]は、
$\therefore K_v=\dfrac{1}{2} m{v_v}^2$ [$\mathrm{J}$] …④ (陽極に電子が達したときの電子の運動エネルギー)
になります。
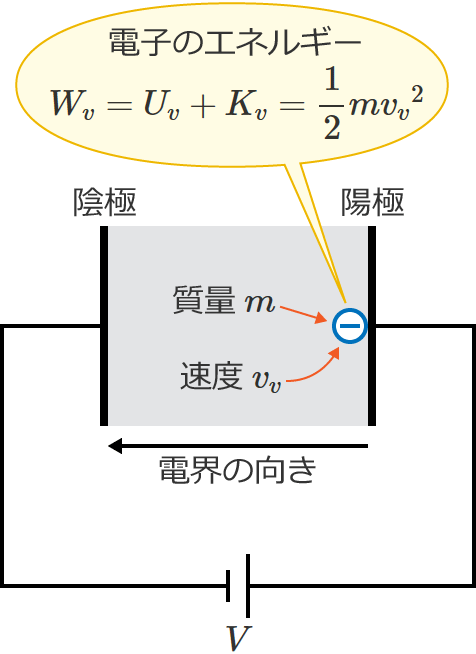
したがって、陽極に電子が達したときの電子のエネルギー $W_v$[$\mathrm{J}$]は、③の位置エネルギーと④の運動エネルギーを足して、
$W_v=U_v+K_v=0+\dfrac{1}{2} m{v_v}^2$ $=\dfrac{1}{2} m{v_v}^2$
$\therefore W_v=\dfrac{1}{2} m{v_v}^2$ [$\mathrm{J}$] (陽極に電子が達したときの電子のエネルギー)
になります。
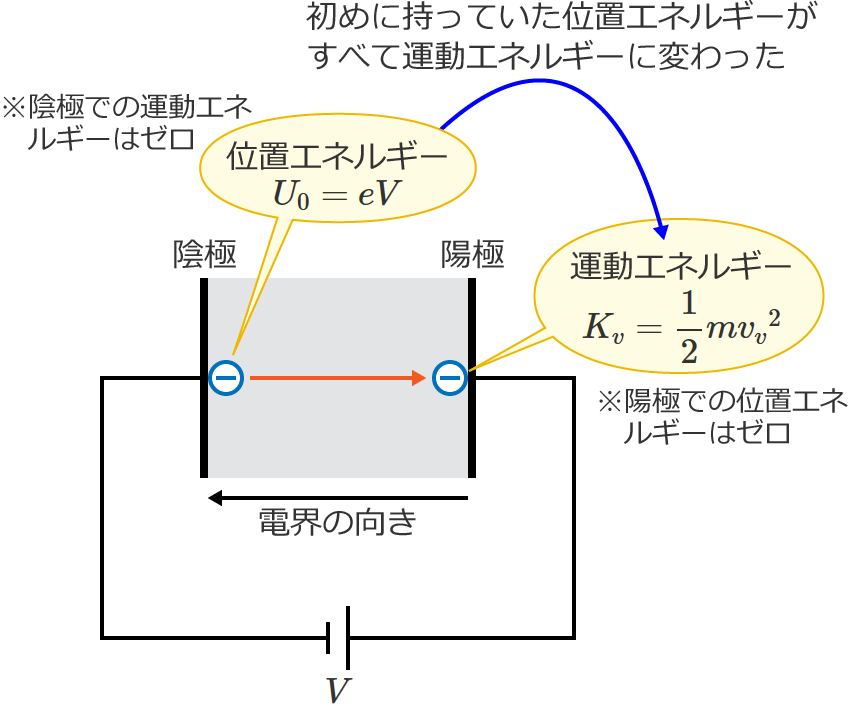
エネルギー保存の法則より物体が持つエネルギーは保存される(エネルギーの合計は変わらない)ので、この場合は、初めに電子が持っていた位置エネルギーが、陽極に達したときにはすべて運動エネルギーに変わったといえます。
このエネルギー保存の法則を使うと、陽極に達したときの電子の速度 $v_v$[$\mathrm{m/s}$]を求めることができます。
では続いて、陽極に達したときの電子の速度 $v_v$[$\mathrm{m/s}$]を求めてみましょう。
電子が陽極に達したときの電子の速度
エネルギー保存の法則より、陰極に電子を置いたときの電子のエネルギー $W_0$[$\mathrm{J}$]と陽極に電子が達したときの電子のエネルギー $W_v$[$\mathrm{J}$]は等しいので、$W_0=W_v$ とすると次の式が成り立ちます。
$eV=\dfrac{1}{2} m{v_v}^2$ …⑤
この⑤式を $v_v$ について解くと、
${v_v}^2=\dfrac{2eV}{m}$
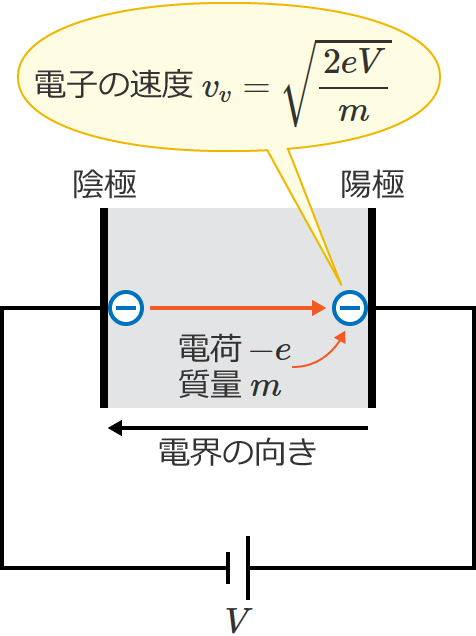
$\therefore v_v=\sqrt{\dfrac{2eV}{m}}$ [$\mathrm{m/s}$] …⑥ (陽極に達したときの電子の速度)
となり、この $v_v$ が陽極に達したときの電子の速度になります。
⑥式中の $e$ は電子の電荷の大きさなので一定の値、$m$ も電子の質量で一定の値になるので、陽極に達したときの電子の速度 $v_v$ は平行平板電極間にかかっている電圧 $V$ の大きさで決まります。
- 陰極に電子を置いたときの電子のエネルギー: $W_0=eV$ [$\mathrm{J}$]
- 陽極に電子が達したときの電子のエネルギー: $W_v=\dfrac{1}{2} m{v_v}^2$ [$\mathrm{J}$]
- 陽極に達したときの電子の速度: $v_v=\sqrt{\dfrac{2eV}{m}}$ [$\mathrm{m/s}$]
スポンサーリンク
スポンサーリンク
電界中で電子が受ける力や、電界中での電子の運動については、こちらの電界中の電子の運動のページを参考にしてみてください。
電位差については、こちらの電位と電位差のページを参考にしてみてください。
スポンサーリンク
電界中の電子のエネルギーと電子が陽極に達したときの速度 関連ページ
- クーロンの法則
- 電気磁気学の「クーロンの法則」について解説しています。クーロンの法則は電気磁気学の中でも特に重要な法則で、電荷間に働く力を求めるときなどに使われます。このページではクーロンの法則をできるだけ簡単に理解できるように、電荷のイメージから解説しています。
- 右ねじの法則
- 電気磁気学の「右ねじの法則」とその使い方についてできるだけ簡単に解説しています。右ねじの法則は電流と磁界の向き(方向)の関係を表わした法則で、アンペールの右ねじの法則とか、アンペアの右ねじの法則と呼ばれたりもします。
- ビオ・サバールの法則
- 電気磁気学の「ビオ・サバールの法則」とその法則を使った磁界の計算方法について解説しています。直線状電流の磁界の計算方法や円形コイル電流の磁界の計算方法はビオ・サバールの法則の使い方の基本になりますので、おぼえておくようにしましょう。
- フレミングの左手の法則と右手の法則
- 「フレミングの左手の法則」と「フレミングの右手の法則」について解説しています。フレミングの左手の法則と右手の法則は、「電流の向き」と「磁界の向き」と「力の向き」の関係を表わした法則で、「力の向き」を求めるときはフレミングの左手の法則、「電流の向き」を求めるときはフレミングの右手の法則を使います。
- 電界中の電子の運動
- 電界中の電子の運動について解説しています。電界中に電子を置いたときや、電界に電子が突入したときの電子の運動について解説していますので、電界中の電子の運動の勉強の参考にしてみてください。
- ローレンツ力
- ローレンツ力について解説しています。ローレンツ力の力の向きや大きさの求め方、円運動などについても解説していますので、ローレンツ力の勉強の参考にしてみてください。
- 電磁誘導
- 電気磁気学の「電磁誘導」と「電磁誘導に関するファラデーの法則」について解説しています。電磁誘導は、コイルを貫く磁束が変化するとコイルに起電力(誘導起電力)が発生する現象です。
- レンツの法則
- 電気磁気学の「レンツの法則」について解説しています。電磁誘導により発生する誘導起電力は、コイルを貫く磁束の変化を妨げるような向きに生じます。これをレンツの法則といいます。


