スポンサーリンク
ローレンツ力
※ページ内にPR・広告が含まれる場合があります。
磁界(磁場)の中で荷電粒子が動くと、荷電粒子は磁界から力を受けます。この荷電粒子が磁界から受ける力をローレンツ力といい、荷電粒子がローレンツ力を受けると荷電粒子の進む方向は曲げられます。

例えば次の図のように磁束密度 $B$[$\mathrm{T}$]の一様な磁界中に、電荷 $+q$[$\mathrm{C}$]の荷電粒子が磁界の向きに垂直に速度 $v$[$\mathrm{m/s}$]で入射したとします。
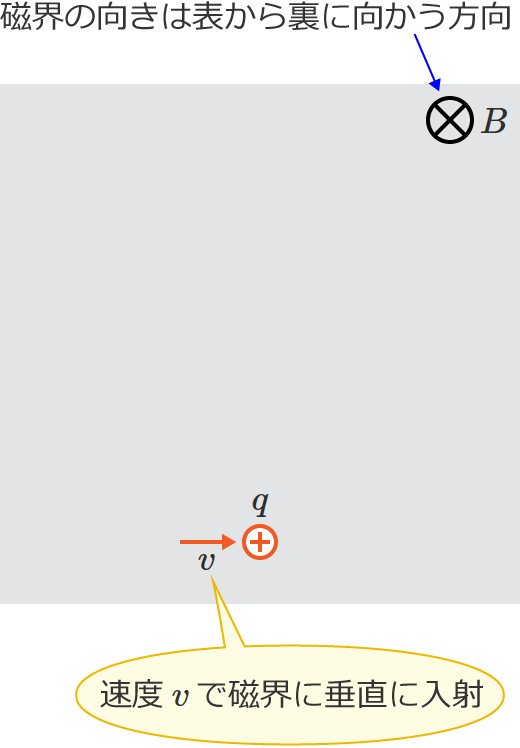
すると、磁界中を動く荷電粒子は速度の向きと垂直な向きに一定の大きさのローレンツ力を受けるので、荷電粒子の進む方向は曲げられ、荷電粒子は等速円運動をします。
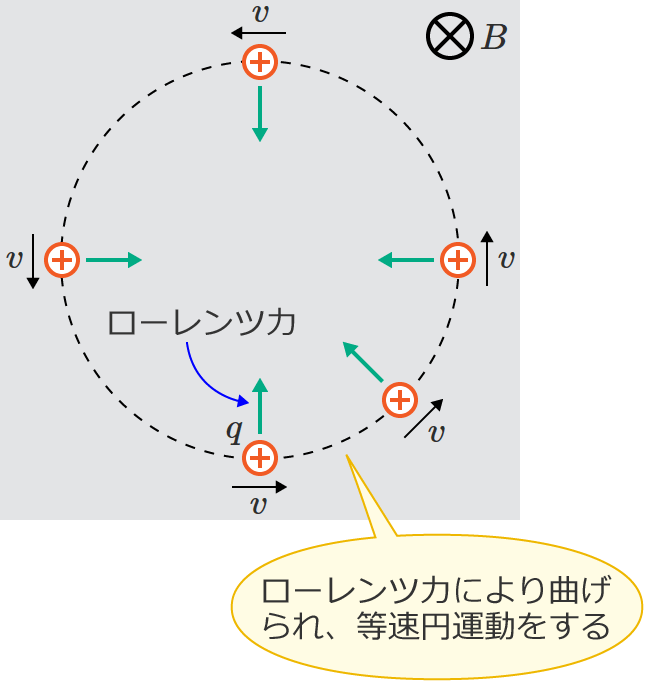
また、次の図のように磁束密度 $B$[$\mathrm{T}$]の一様な磁界中に、電荷 $+q$[$\mathrm{C}$]の荷電粒子が磁界の外から速度 $v$[$\mathrm{m/s}$]で入射したとすると、この場合も荷電粒子はローレンツ力を受け、荷電粒子は次の図のように半周して磁界の外に出ていきます。
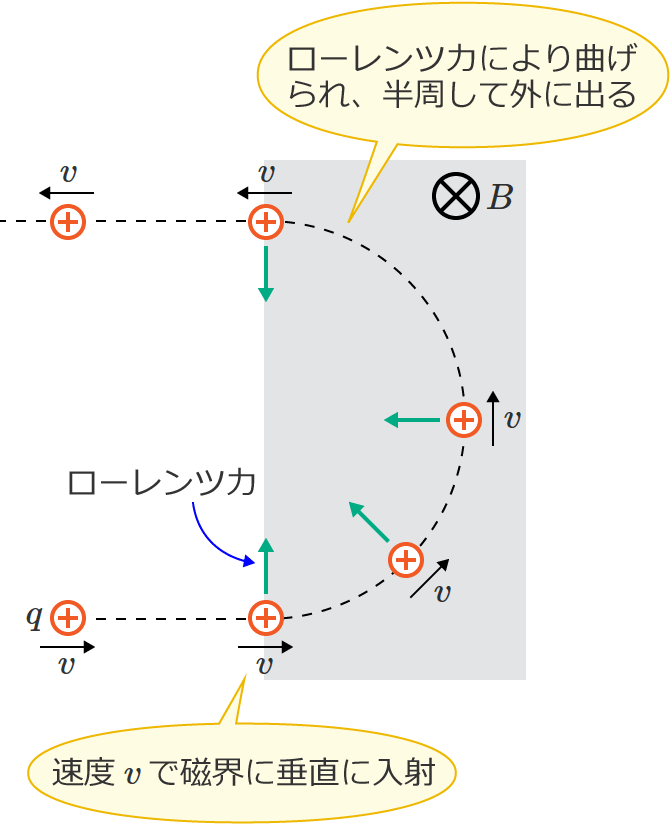
このように磁界中で荷電粒子が動くと、ローレンツ力により荷電粒子の進む方向が曲げられます。
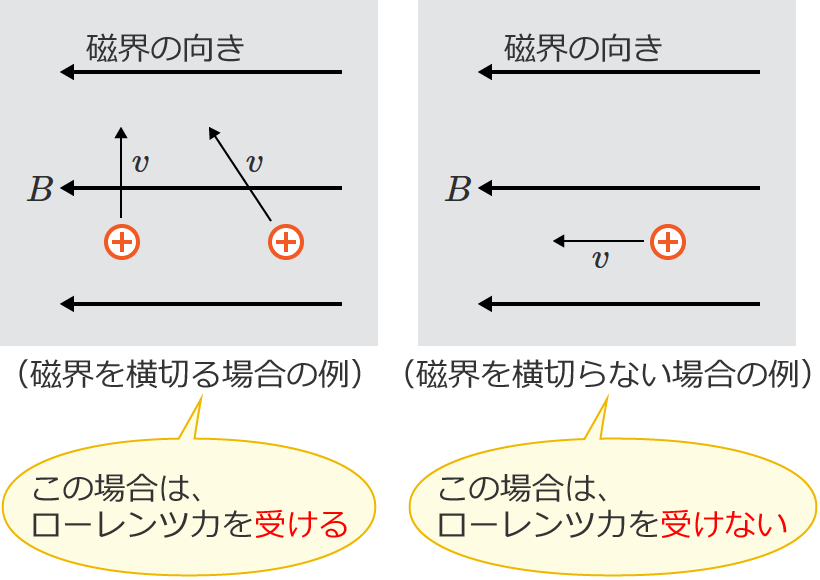
ちなみに、磁界中で荷電粒子が動く場合であっても、次の図のように荷電粒子の速度の向きが磁界の向きと同じ場合にはローレンツ力を受けないので、荷電粒子は曲がらずに等速直線運動をします。
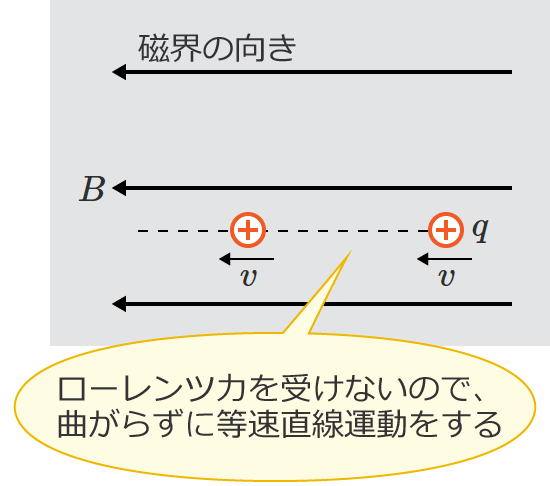
磁界を横切るときはローレンツ力を受けるけど、磁界を横切らないときはローレンツ力を受けないよ、ということです。
スポンサーリンク
ローレンツ力の向き
次の図のように磁束密度 $B$[$\mathrm{T}$]の一様な磁界中に、電荷 $+q$[$\mathrm{C}$]の荷電粒子が磁界の向きに垂直に速度 $v$[$\mathrm{m/s}$]で入射したとします。
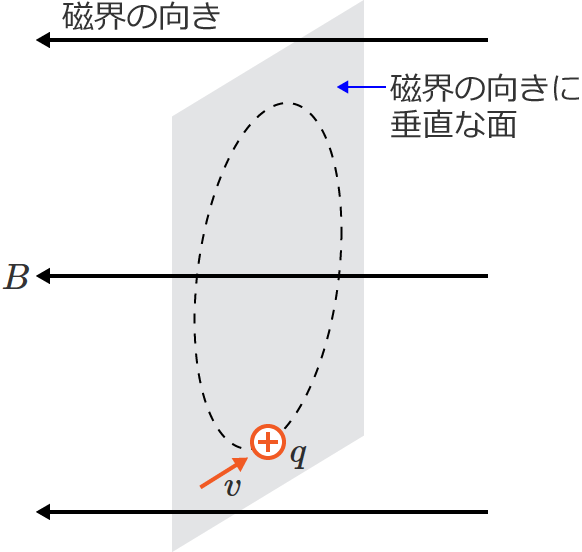
このとき、荷電粒子が受けるローレンツ力の向きは「速度の向き」と「磁界の向き」のどちらに対しても垂直な向きになり、その向きはフレミングの左手の法則の「力の向き」を示す方向と同じになります。
なので、ローレンツ力の力の向きを知りたいときは、フレミングの左手の法則で力の向きを求めるときと同じように、
- フレミングの左手の法則の中指(電流の向き)に「荷電粒子の速度の向き」をあてはめる(プラスの荷電粒子が移動する向きを電流の向きと考えます)
- フレミングの左手の法則の人差し指(磁界の向き)に「磁界の向き」をあてはめる
とすると、親指(力の向き)がローレンツ力の力の向きになります。
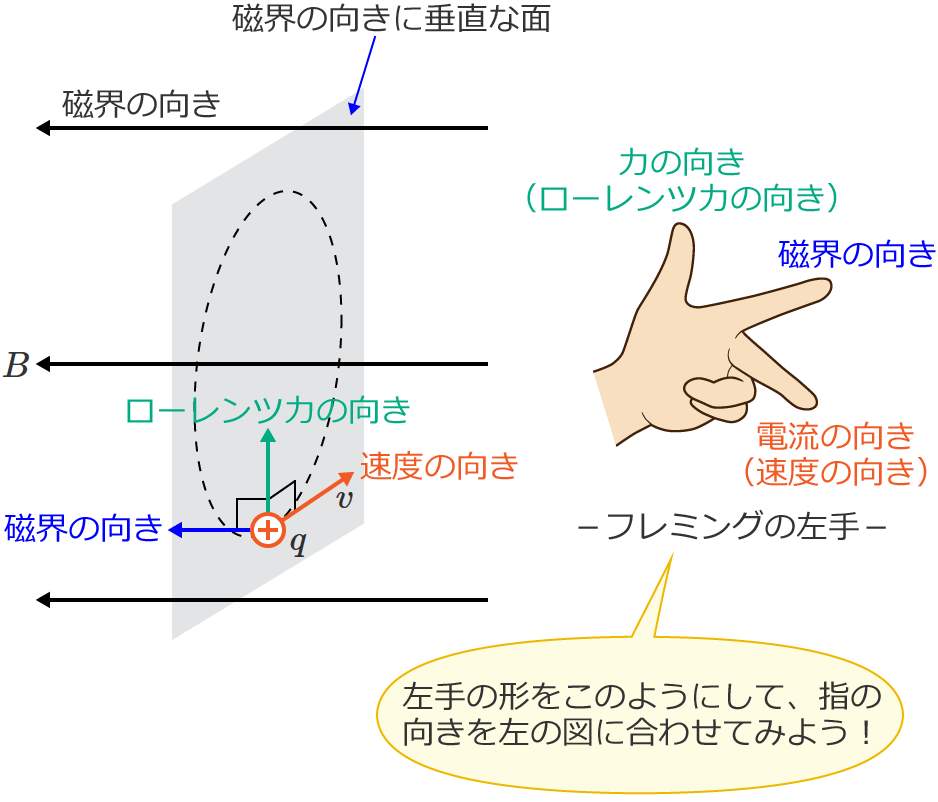
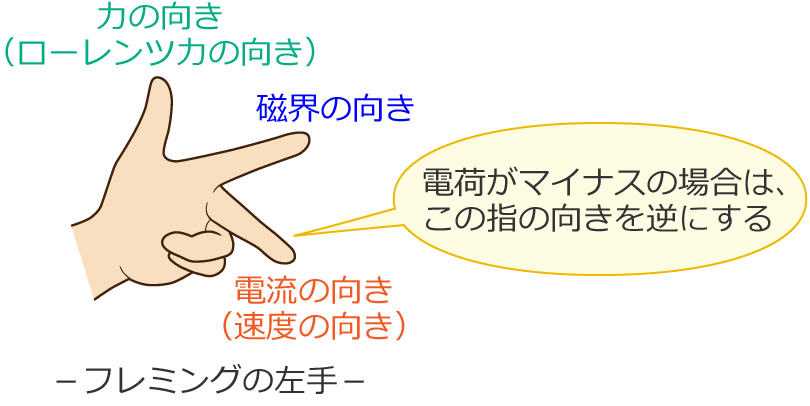
ただし、フレミングの左手の法則の中指(電流の向き)に「荷電粒子の速度の向き」をそのままあてはめられるのは、荷電粒子の電荷がプラスの場合です。
荷電粒子の電荷が、例えば電子のようにマイナスの電荷の場合には、中指の向きを荷電粒子の速度の向きと逆にします。
フレミングの法則については、こちらのフレミングの左手の法則と右手の法則のページを参考にしてみてください。
スポンサーリンク
スポンサーリンク
ローレンツ力の大きさ
ローレンツ力の大きさ $F$[$\mathrm{N}$]は、荷電粒子の電荷の大きさを $q$[$\mathrm{C}$]、荷電粒子の速度を $v$[$\mathrm{m/s}$]、磁束密度を $B$[$\mathrm{T}$]、荷電粒子の速度の向きと磁界の向きのなす角を $\theta$ とすると、
$F=qvB\sin\theta$ [$\mathrm{N}$] …① (ローレンツ力の大きさ)
と表わされます。
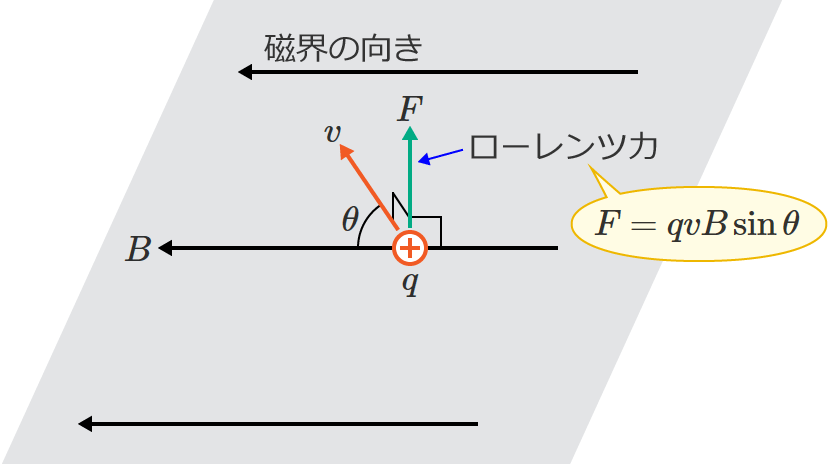
①式中の $\theta$ は「荷電粒子の速度の向き」と「磁界の向き」のなす角なので、2つの向きのなす角が $90^{\circ}$ の場合は、①式中の $\sin\theta$ は $\sin\theta =\sin 90^{\circ} =1$ となり、このときのローレンツ力の大きさは、
$F=qvB$ [$\mathrm{N}$] (速度の向きと磁界の向きが垂直の場合のローレンツ力の大きさ)
になります。
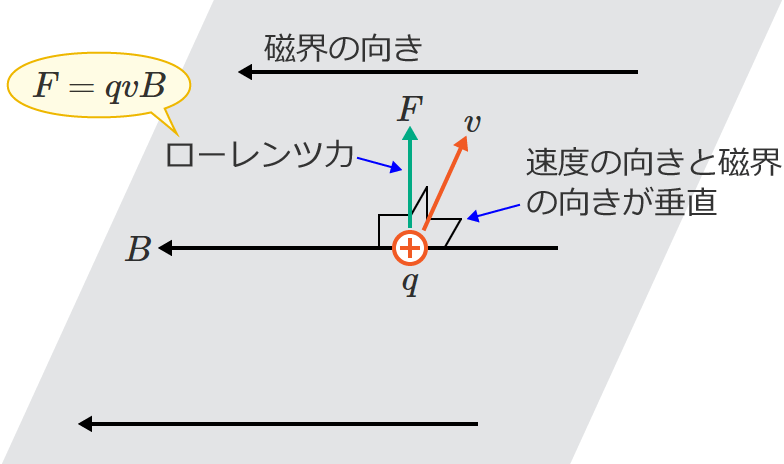
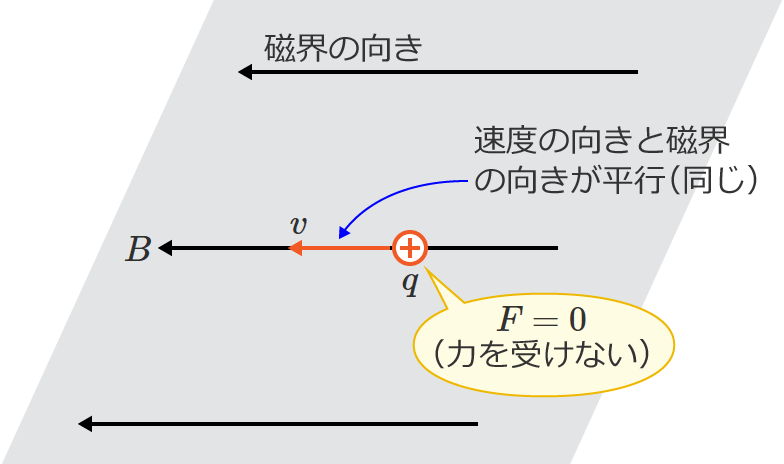
また、「荷電粒子の速度の向き」と「磁界の向き」が平行な場合は、2つの向きのなす角が $0^{\circ}$ になるので、①式中の $\sin\theta$ は $\sin\theta =\sin 0^{\circ} =0$ となり、このときのローレンツ力の大きさは、
$F=0$ [$\mathrm{N}$] (速度の向きと磁界の向きが平行の場合のローレンツ力の大きさ)
になります。つまり、「荷電粒子の速度の向き」と「磁界の向き」が同じ場合は、ローレンツ力がゼロなので荷電粒子は力を受けず、荷電粒子は曲がらずにまっすぐ等速直線運動をします。
ローレンツ力による円運動
一様な磁界中に垂直に荷電粒子が入射すると、荷電粒子には、荷電粒子の速度の向きに常に垂直で一定の大きさのローレンツ力がはたらきます。
そのため、このローレンツ力が向心力となって、荷電粒子は磁界中で等速円運動をします。
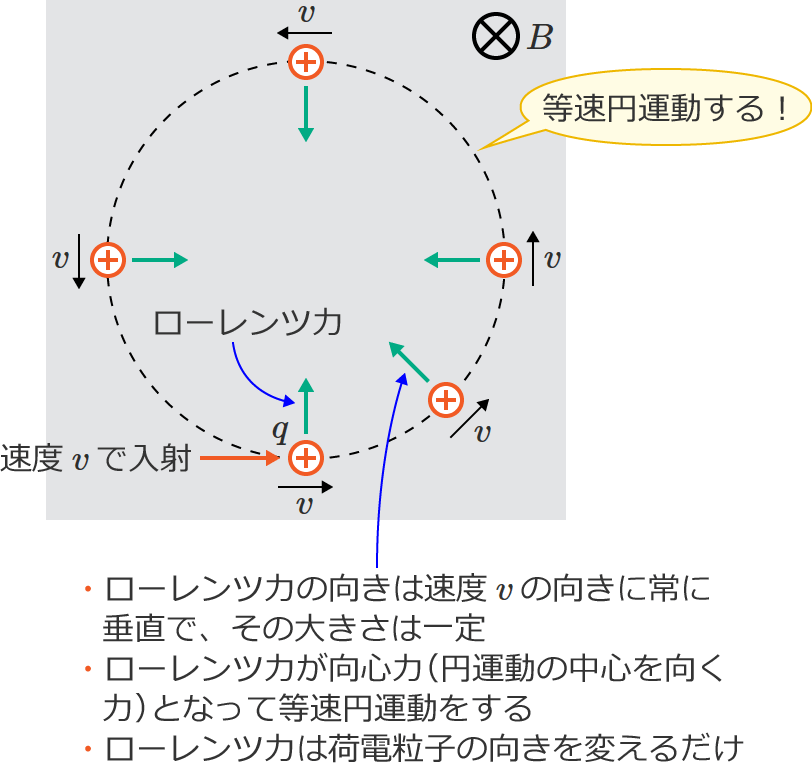
ローレンツ力の向きは荷電粒子の速度の向きに常に垂直になるので、ローレンツ力は荷電粒子に仕事をしません。なので、荷電粒子の速さは変わらず一定で、向きだけが変わります。
この等速円運動の半径、周期、角周波数は、以下のように計算すると求めることができます。
ローレンツ力による円運動の半径
ローレンツ力により荷電粒子が円運動しているときは、「ローレンツ力による向心力」と「円運動の遠心力」がつり合っている状態になっているので、このつり合いから円運動の半径を求めることができます。
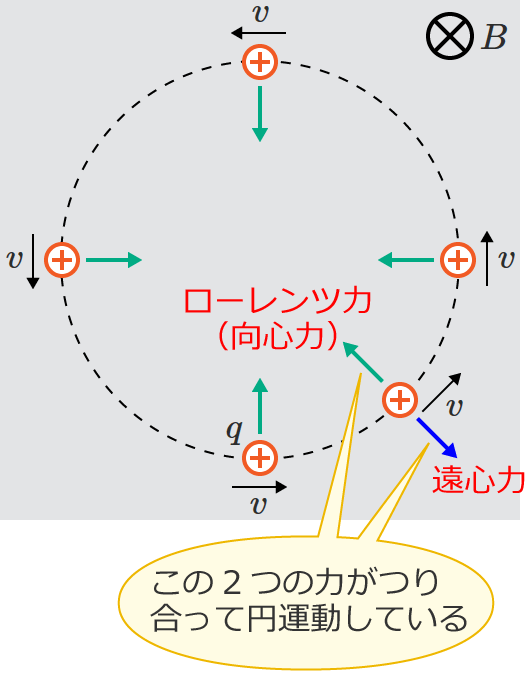
この場合のローレンツ力 $F$[$\mathrm{N}$]は、荷電粒子の電荷の大きさを $q$[$\mathrm{C}$]、荷電粒子の速度を $v$[$\mathrm{m/s}$]、磁束密度を $B$[$\mathrm{T}$]とすると、
$F=qvB$ …②
になります。また、遠心力 $F_c$[$\mathrm{N}$]は、荷電粒子の質量を $m$[$\mathrm{kg}$]、荷電粒子の速度を $v$[$\mathrm{m/s}$]、円運動の半径を $r$[$\mathrm{m}$]とすると、
$F_c=\dfrac{mv^2}{r}$ …③
になります。ローレンツ力により荷電粒子が円運動しているときは、②と③がつり合っている状態なので、②=③として運動方程式をたてると、
$qvB=\dfrac{mv^2}{r}$ …④
となります。この④式を半径 $r$ について解くと、
$r=\dfrac{mv^2}{qvB} =\dfrac{mv}{qB}$
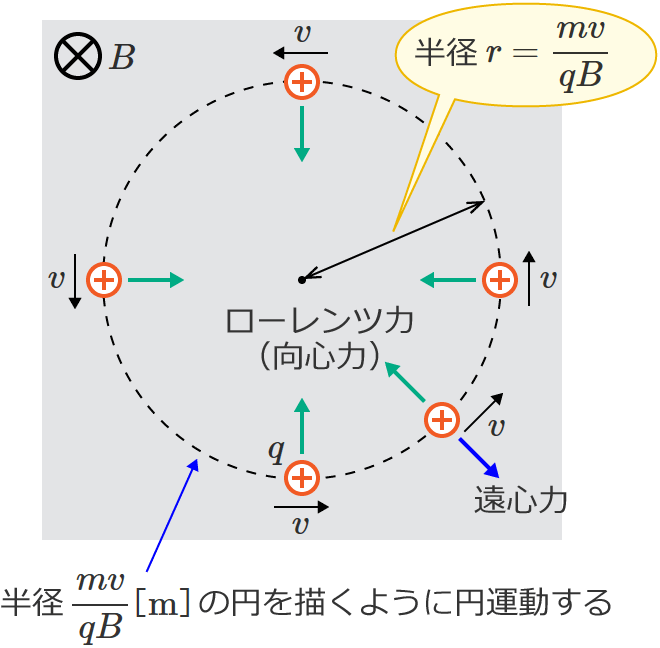
$\therefore r=\dfrac{mv}{qB}$ [$\mathrm{m}$] (円運動の半径)
となり、この $r$ がローレンツ力による円運動の半径になります。
なので、荷電粒子は半径 $\dfrac{mv}{qB}$[$\mathrm{m}$]の円を描くように円運動するよ、ということになります。
ローレンツ力による円運動の周期
半径 $r$[$\mathrm{m}$]の円周上を速度 $v$[$\mathrm{m/s}$]で等速円運動している物体の周期 $T$[$\mathrm{s}$]は、
$T=\dfrac{2\pi r}{v}$ …⑤
で表わされるので、この⑤式にさきほど求めた半径 $r=\dfrac{mv}{qB}$ を代入すると、
$T=\dfrac{2\pi r}{v} =\dfrac{2\pi}{v}\times\dfrac{mv}{qB} =\dfrac{2\pi m}{qB}$
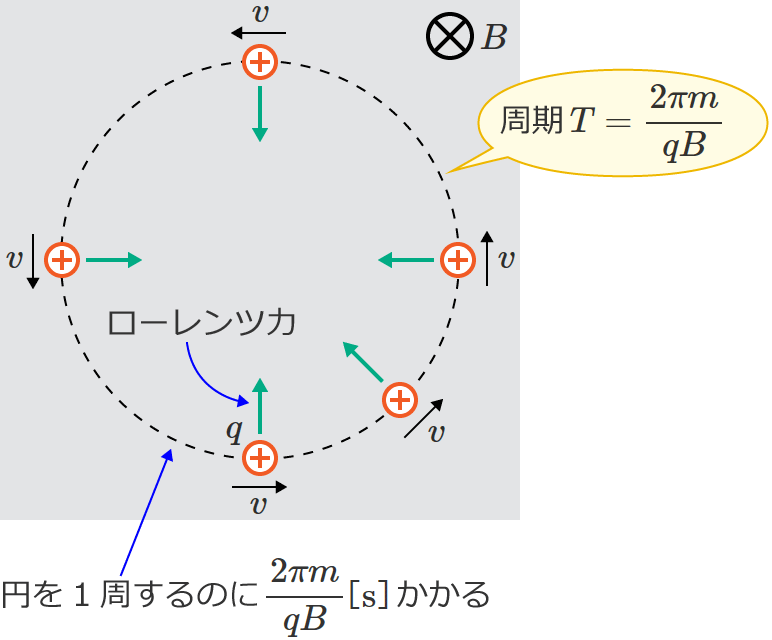
$\therefore T=\dfrac{2\pi m}{qB}$ [$\mathrm{s}$] (円運動の周期)
となり、この $T$ がローレンツ力による円運動の周期になります。
円運動の周期は「円を1周するのにかかる時間」なので、荷電粒子が円を1周するのに $\dfrac{2\pi m}{qB}$[$\mathrm{s}$]かかるよ、ということになります。(ちょっと言い換えれば、「荷電粒子が1周してまた元の位置に戻ってくるのは $\dfrac{2\pi m}{qB}$[$\mathrm{s}$]後」とも言えます。)
ローレンツ力による円運動の角周波数
角周波数 $\omega$[$\mathrm{rad/s}$]と周期 $T$[$\mathrm{s}$]の関係は、
$\omega =\dfrac{2\pi}{T}$ …⑥
で表わされるので、この⑥式にさきほど求めた周期 $T=\dfrac{2\pi m}{qB}$ を代入すると、
$\omega =\dfrac{2\pi}{T} =\dfrac{2\pi}{\dfrac{2\pi m}{qB}} =2\pi\times\dfrac{qB}{2\pi m}$ $=\dfrac{qB}{m}$
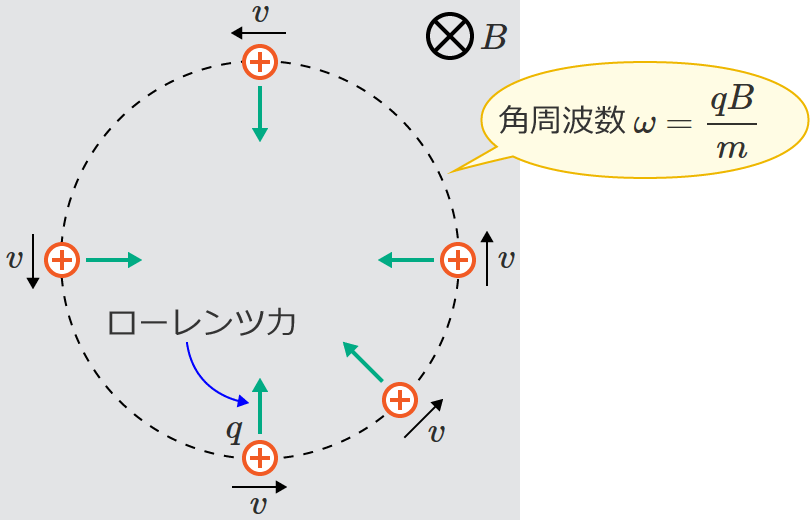
$\therefore \omega =\dfrac{qB}{m}$ [$\mathrm{rad/s}$] (円運動の角周波数)
となり、この $\omega$ がローレンツ力による円運動の角周波数になります。
荷電粒子が磁界に斜めに入射するとらせん運動する
荷電粒子が磁界に垂直に入射すると円運動しますが、荷電粒子が磁界に斜めに入射すると荷電粒子はらせん運動をします。
これは、荷電粒子が磁界に斜めに入射したときの速度の磁界と平行な向きの速度成分によるもので、入射した荷電粒子の速度を $v$[$\mathrm{m/s}$]とすると、磁界と平行な向きに速度 $v\cos\theta$[$\mathrm{m/s}$]で進むためです。( $\theta$ は「斜めに入射した荷電粒子の速度の向き」と「磁界の向き」のなす角です。)
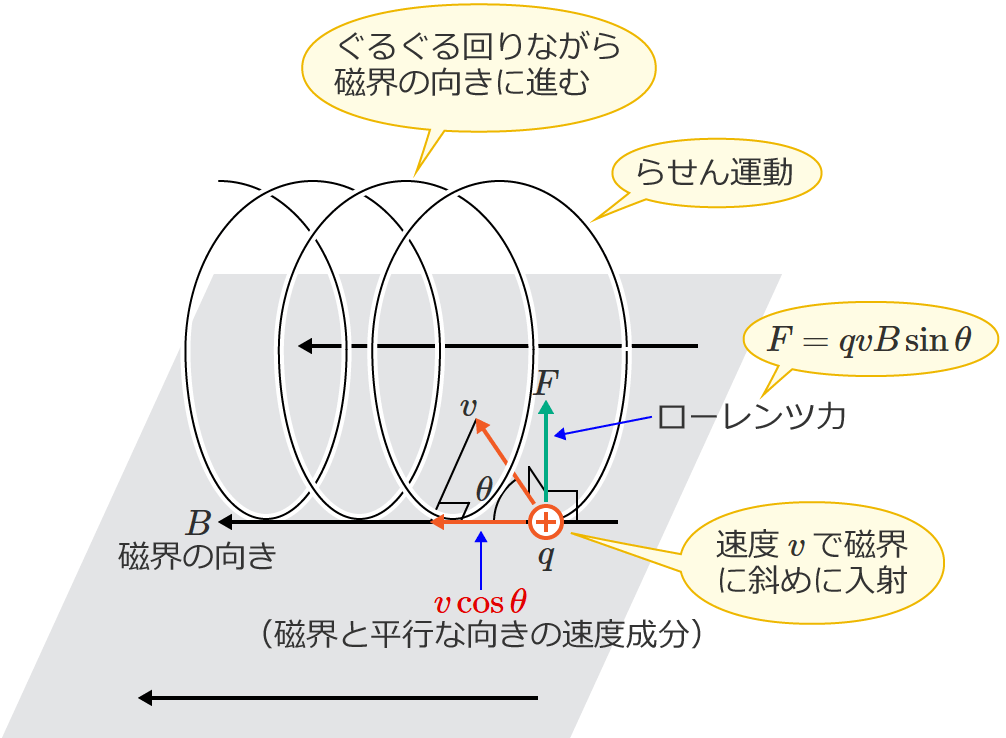
以上のように、磁界中で荷電粒子がローレンツ力を受けると荷電粒子の進む方向は曲げられ、荷電粒子は「円運動」や「らせん運動」をします。
- 磁界の中で荷電粒子が動くと荷電粒子は磁界から力を受ける。この荷電粒子が受ける力をローレンツ力という
- ローレンツ力の力の向きはフレミングの左手を使うと分かる
- ローレンツ力の大きさ: $F=qvB\sin\theta$
- 磁界中に垂直に荷電粒子が入射すると、荷電粒子は円運動をする
- 磁界中に斜めに荷電粒子が入射すると、荷電粒子はらせん運動をする
スポンサーリンク
スポンサーリンク
電界中の電子の運動については、こちらの電界中の電子の運動のページを参考にしてみてください。
電界中の電子のエネルギーと電子が陽極に達したときの速度 ←BACK
NEXT→ 電磁誘導
スポンサーリンク
ローレンツ力 関連ページ
- クーロンの法則
- 電気磁気学の「クーロンの法則」について解説しています。クーロンの法則は電気磁気学の中でも特に重要な法則で、電荷間に働く力を求めるときなどに使われます。このページではクーロンの法則をできるだけ簡単に理解できるように、電荷のイメージから解説しています。
- 右ねじの法則
- 電気磁気学の「右ねじの法則」とその使い方についてできるだけ簡単に解説しています。右ねじの法則は電流と磁界の向き(方向)の関係を表わした法則で、アンペールの右ねじの法則とか、アンペアの右ねじの法則と呼ばれたりもします。
- ビオ・サバールの法則
- 電気磁気学の「ビオ・サバールの法則」とその法則を使った磁界の計算方法について解説しています。直線状電流の磁界の計算方法や円形コイル電流の磁界の計算方法はビオ・サバールの法則の使い方の基本になりますので、おぼえておくようにしましょう。
- フレミングの左手の法則と右手の法則
- 「フレミングの左手の法則」と「フレミングの右手の法則」について解説しています。フレミングの左手の法則と右手の法則は、「電流の向き」と「磁界の向き」と「力の向き」の関係を表わした法則で、「力の向き」を求めるときはフレミングの左手の法則、「電流の向き」を求めるときはフレミングの右手の法則を使います。
- 電界中の電子の運動
- 電界中の電子の運動について解説しています。電界中に電子を置いたときや、電界に電子が突入したときの電子の運動について解説していますので、電界中の電子の運動の勉強の参考にしてみてください。
- 電界中の電子のエネルギーと電子が陽極に達したときの速度
- 電界中の電子のエネルギーと電子が陽極に達したときの速度について解説しています。電界中の電子の位置エネルギーや運動エネルギーなどについて解説していますので、電界中の電子のエネルギーの勉強の参考にしてみてください。
- 電磁誘導
- 電気磁気学の「電磁誘導」と「電磁誘導に関するファラデーの法則」について解説しています。電磁誘導は、コイルを貫く磁束が変化するとコイルに起電力(誘導起電力)が発生する現象です。
- レンツの法則
- 電気磁気学の「レンツの法則」について解説しています。電磁誘導により発生する誘導起電力は、コイルを貫く磁束の変化を妨げるような向きに生じます。これをレンツの法則といいます。


