電気のお勉強｜電気磁気学｜電磁誘導

スポンサーリンク

コイルを貫く磁束が変化すると、コイルに起電力（電圧）が発生します。この現象を電磁誘導といい、このときにコイルに発生する起電力を誘導起電力、コイルに流れる電流を誘導電流といいます。

 

 

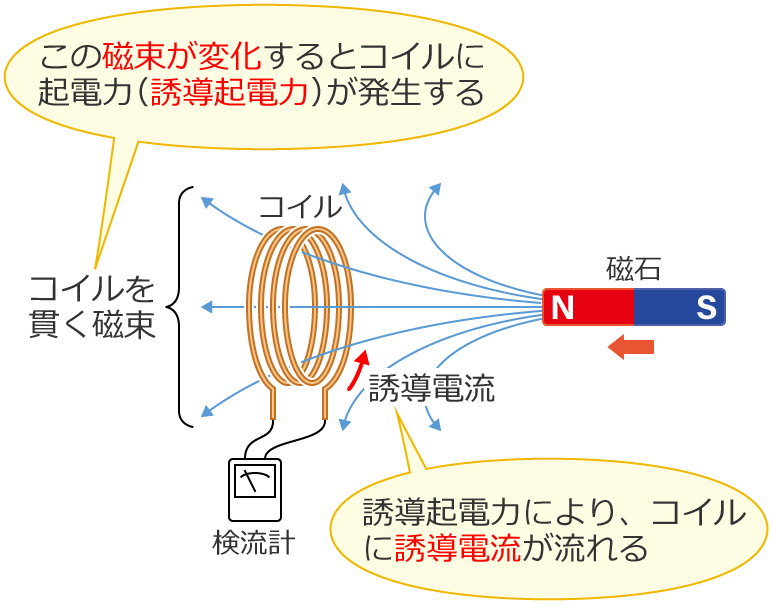
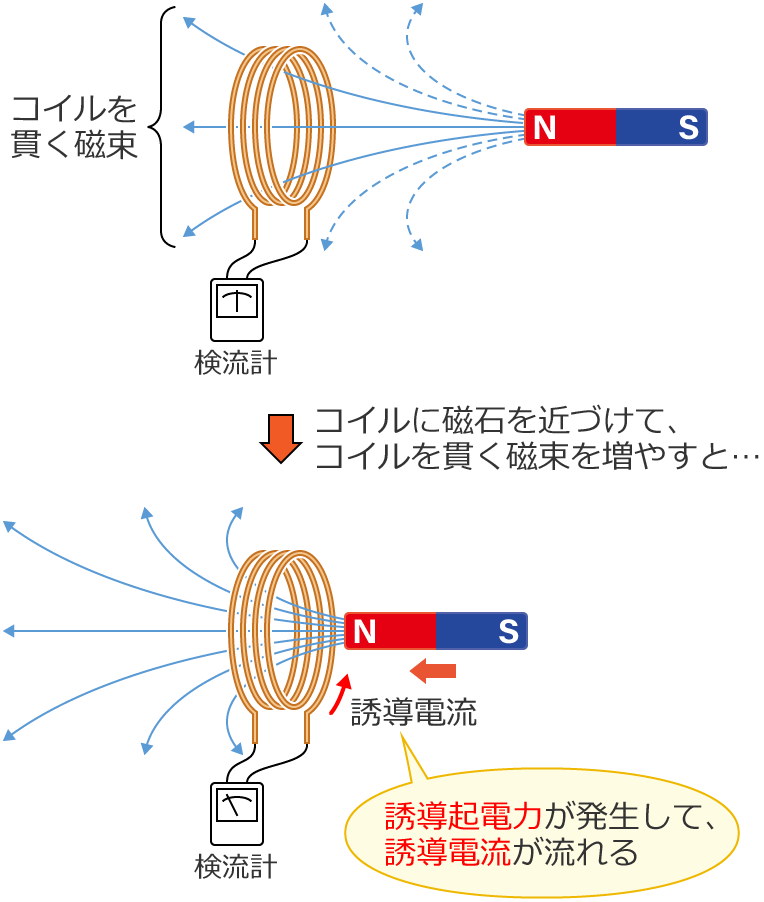
例えば、次のようにコイルに磁石を近づけると、コイルを貫く磁束は増加（変化）するので、コイルには誘導起電力が発生してコイルに誘導電流が流れます。

 

 

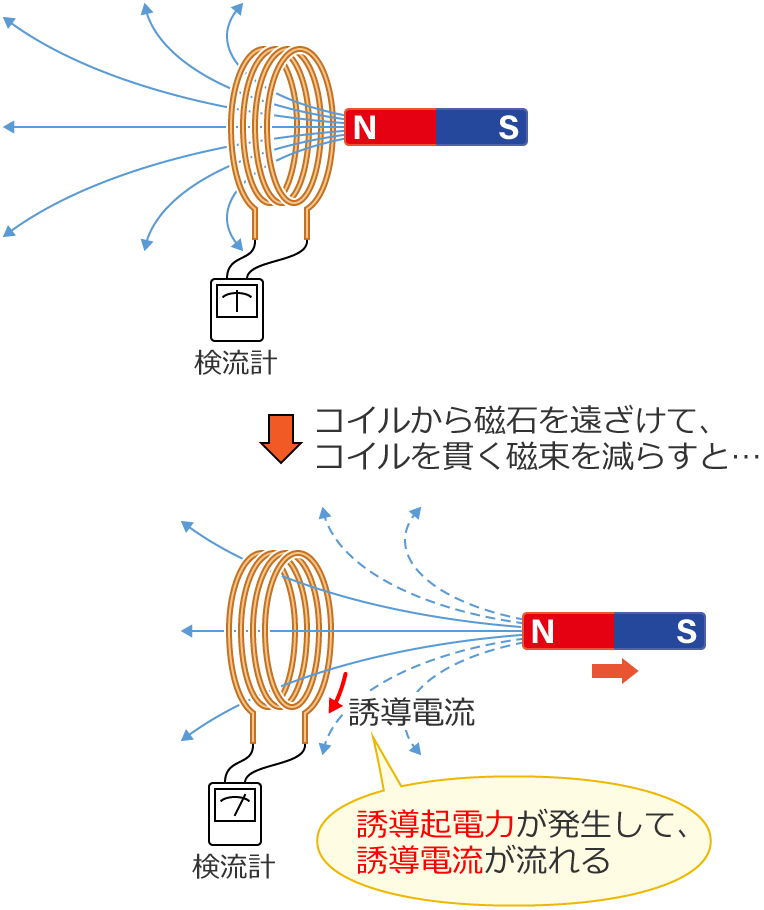
また反対に、コイルから磁石を遠ざけると、コイルを貫く磁束は減少（変化）するので、このときもコイルには誘導起電力が発生してコイルに誘導電流が流れます。

 

 

このように、コイルを貫く磁束が時間的に変化（時間に対して増加または減少）することによって、コイルに誘導起電力が発生する現象が電磁誘導です。

 

 

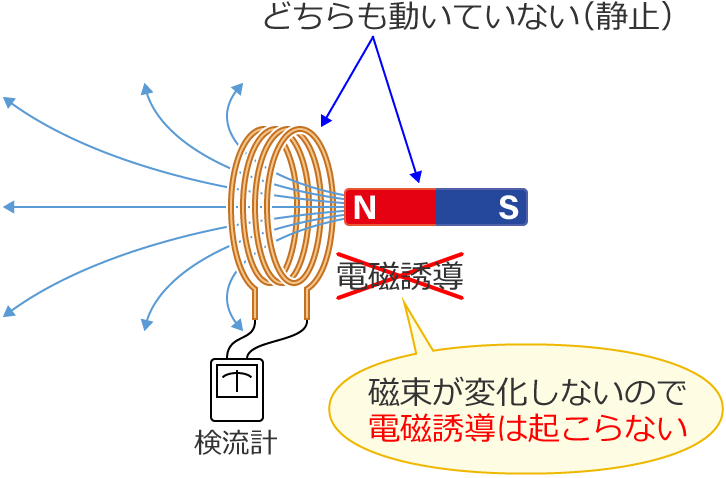
ちなみに、誘導起電力が発生するのはコイルを貫く磁束が時間的に変化している間だけなので、次のように磁石とコイルを動かさないで静止させている場合には、磁束がコイルを通っていても電磁誘導は起こりません。

 

 

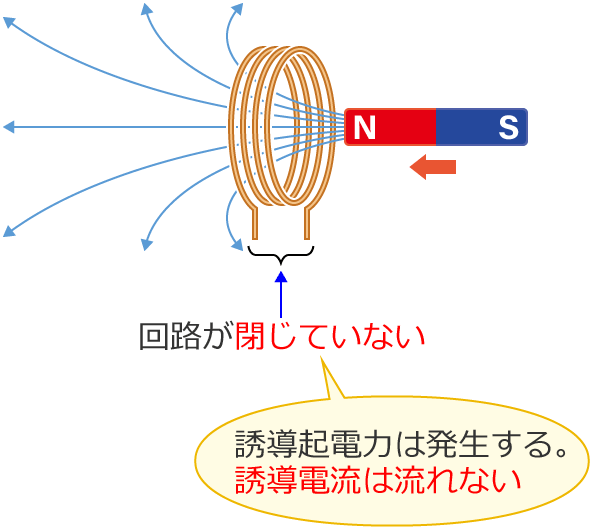
また、コイルの回路が閉回路になっていない場合は、誘導起電力は発生しますが誘導電流は流れません。これは、回路が閉回路になっていないと（回路が閉じていないと）電流は流れることができないからです。

 

 

 

電磁誘導に関するファラデーの法則

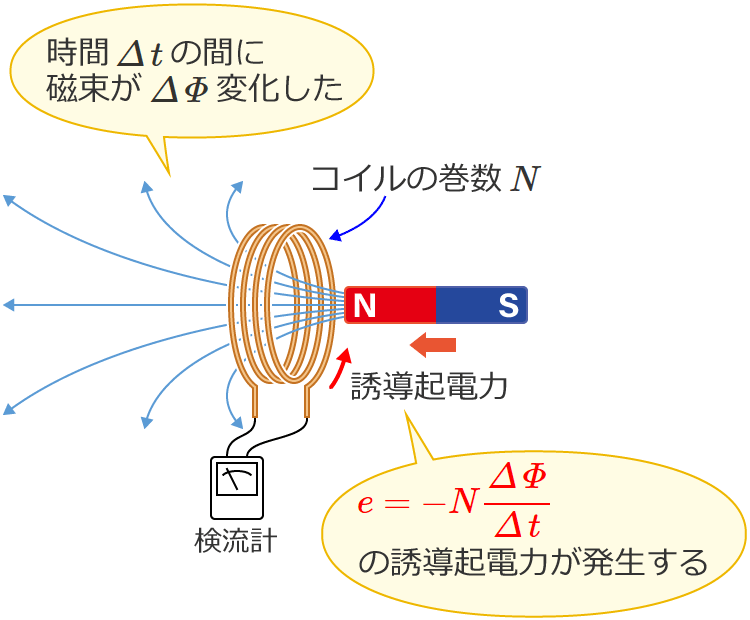
電磁誘導によって発生する誘導起電力は、コイルを貫く磁束の単位時間あたりの変化に比例します。これを電磁誘導に関するファラデーの法則といい、$N$ 回巻きのコイルを貫く磁束が時間 $\varDelta\, t$［$\mathrm{s}$］の間に $\varDelta\,\varPhi$［$\mathrm{Wb}$］変化したとすると、このときに発生する誘導起電力 $e$［$\mathrm{V}$］は、

 

$e=-N\dfrac{\varDelta\,\varPhi}{\varDelta\, t}$　…①

 

と表わされます。

 

 

 

①式をみると分かるように、電磁誘導によって発生する誘導起電力の大きさは、コイルの巻数 $N$、コイルを貫く磁束の変化 $\varDelta\,\varPhi$、磁束が変化する間の時間 $\varDelta\, t$ によって決まります。

 

コイルの巻数と誘導起電力の大きさの関係

 

$e=-N\dfrac{\varDelta\,\varPhi}{\varDelta\, t}$　…①

 

①式より、電磁誘導によって発生する誘導起電力 $e$ の大きさはコイルの巻数 $N$ に比例するので、コイルの巻数 $N$ を大きくする（巻数を多くする）と誘導起電力 $e$ の大きさは大きくなり、コイルの巻数 $N$ を小さくする（巻数を少なくする）と誘導起電力 $e$ の大きさは小さくなります。

 

 

コイルを貫く磁束の変化と誘導起電力の大きさの関係

 

$e=-N\dfrac{\varDelta\,\varPhi}{\varDelta\, t}$　…①

 

①式より、電磁誘導によって発生する誘導起電力 $e$ の大きさはコイルを貫く磁束の変化 $\varDelta\,\varPhi$ に比例するので、コイルを貫く磁束の変化 $\varDelta\,\varPhi$ を大きくする（磁束の変化前と変化後の差を大きくする）と誘導起電力 $e$ の大きさは大きくなり、コイルを貫く磁束の変化 $\varDelta\,\varPhi$ を小さくする（磁束の変化前と変化後の差を小さくする）と誘導起電力 $e$ の大きさは小さくなります。

 

 

 

また①式より、$\varDelta\,\varPhi =0$ のときは $e=0$ になるので、磁束の変化がない場合（磁束が変化しない場合）は誘導起電力は発生しません。

 

 

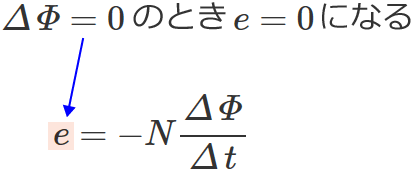
つまり、磁石とコイルを動かさないでどちらも静止させている場合は、磁束がコイルを通っていても誘導起電力は発生しませんよ、ということです。

 

磁束が変化する間の時間と誘導起電力の大きさの関係

 

$e=-N\dfrac{\varDelta\,\varPhi}{\varDelta\, t}$　…①

 

①式より、電磁誘導によって発生する誘導起電力 $e$ の大きさは磁束が変化する間の時間 $\varDelta\, t$ に反比例するので、磁束が変化する間の時間 $\varDelta\, t$ を大きくする（磁石をゆっくり動かす）と誘導起電力 $e$ の大きさは小さくなり、磁束が変化する間の時間 $\varDelta\, t$ を小さくする（磁石を素早く動かす）と誘導起電力 $e$ の大きさは大きくなります。

 

 

以上のことから、

• コイルの巻数を増やす
• 磁力が強い磁石を使う
• 磁石を素早く動かす

と、電磁誘導によって発生する誘導起電力を大きくすることができます。

 

電磁誘導による誘導起電力の計算例

$200\,$回巻きのコイルを貫く磁束が $0.2\,$秒の間に $0.1\,\mathrm{Wb}$ 増加した。このとき、コイルに発生する誘導起電力の大きさは？

 

コイルの巻数 $N=200\,$回、コイルを貫く磁束の変化 $\varDelta\,\varPhi =0.1\,\mathrm{Wb}$ 、磁束が変化する間の時間 $\varDelta\, t=0.2\,\mathrm{s}$ なので、これらの値を①式に代入すると、

 

$e=-N\dfrac{\varDelta\,\varPhi}{\varDelta\, t}$

 

$=-200\times\dfrac{0.1}{0.2} =-200\times\dfrac{1}{2}$ $=-100$

 

求めるのは誘導起電力の大きさなのでマイナスはとって、

 

$\therefore$ 誘導起電力の大きさ $=100\mathrm{V}$

 

となります。

 

 

 

ローレンツ力　←BACK

NEXT→　レンツの法則

スポンサーリンク

電磁誘導　関連ページ

クーロンの法則

電気磁気学の「クーロンの法則」について解説しています。クーロンの法則は電気磁気学の中でも特に重要な法則で、電荷間に働く力を求めるときなどに使われます。このページではクーロンの法則をできるだけ簡単に理解できるように、電荷のイメージから解説しています。

右ねじの法則

電気磁気学の「右ねじの法則」とその使い方についてできるだけ簡単に解説しています。右ねじの法則は電流と磁界の向き（方向）の関係を表わした法則で、アンペールの右ねじの法則とか、アンペアの右ねじの法則と呼ばれたりもします。

ビオ・サバールの法則

電気磁気学の「ビオ・サバールの法則」とその法則を使った磁界の計算方法について解説しています。直線状電流の磁界の計算方法や円形コイル電流の磁界の計算方法はビオ・サバールの法則の使い方の基本になりますので、おぼえておくようにしましょう。

フレミングの左手の法則と右手の法則

「フレミングの左手の法則」と「フレミングの右手の法則」について解説しています。フレミングの左手の法則と右手の法則は、「電流の向き」と「磁界の向き」と「力の向き」の関係を表わした法則で、「力の向き」を求めるときはフレミングの左手の法則、「電流の向き」を求めるときはフレミングの右手の法則を使います。

電界中の電子の運動

電界中の電子の運動について解説しています。電界中に電子を置いたときや、電界に電子が突入したときの電子の運動について解説していますので、電界中の電子の運動の勉強の参考にしてみてください。

電界中の電子のエネルギーと電子が陽極に達したときの速度

電界中の電子のエネルギーと電子が陽極に達したときの速度について解説しています。電界中の電子の位置エネルギーや運動エネルギーなどについて解説していますので、電界中の電子のエネルギーの勉強の参考にしてみてください。

ローレンツ力

ローレンツ力について解説しています。ローレンツ力の力の向きや大きさの求め方、円運動などについても解説していますので、ローレンツ力の勉強の参考にしてみてください。

レンツの法則

電気磁気学の「レンツの法則」について解説しています。電磁誘導により発生する誘導起電力は、コイルを貫く磁束の変化を妨げるような向きに生じます。これをレンツの法則といいます。