スター結線（Y結線）の線間電圧はなぜ相電圧の√3倍になるのか？

※ページ内にPR･広告が含まれる場合があります。

スター結線（Y結線）の線間電圧と相電圧の関係式

スター結線（Y結線）されている三相交流回路の線間電圧と相電圧の関係は、

線間電圧 $=\sqrt{3} \ \times$ 相電圧　…①

となり、この関係式はスター結線（Y結線）の三相交流回路を考えるときによく使われていて、ほぼ公式みたいなものです。（てか、公式か？）

この関係式（①式）は三相交流の問題を解くときなどに使ったことがある人が多いと思いますが、

なぜ、線間電圧は相電圧の $\sqrt{3}$ 倍になるの？

って、思ったりしますよね？　ない？

ここでは、スター結線（Y結線）のときに、線間電圧が相電圧の $\sqrt{3}$ 倍になる理由について解説します。

スター結線で線間電圧が相電圧の√3倍になる理由

次の図のようなスター結線（Y結線）された三相交流回路について考えます。

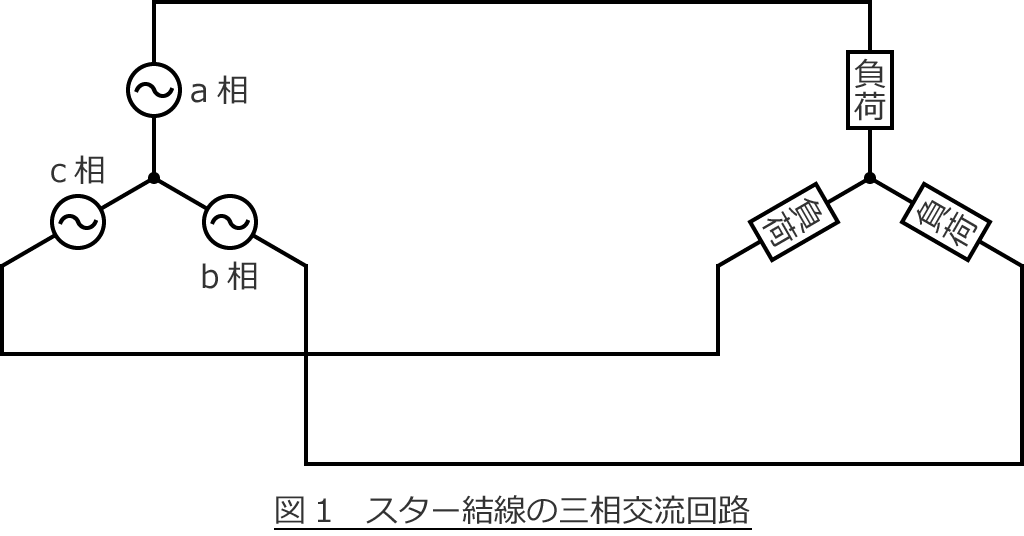
図1　スター結線（Y結線）の三相交流回路

この回路図を見て、あれ？線間電圧と相電圧ってどこの電圧だったっけ？

なんて、思っちゃったりしていないですか？

線間電圧と相電圧はここですよ！

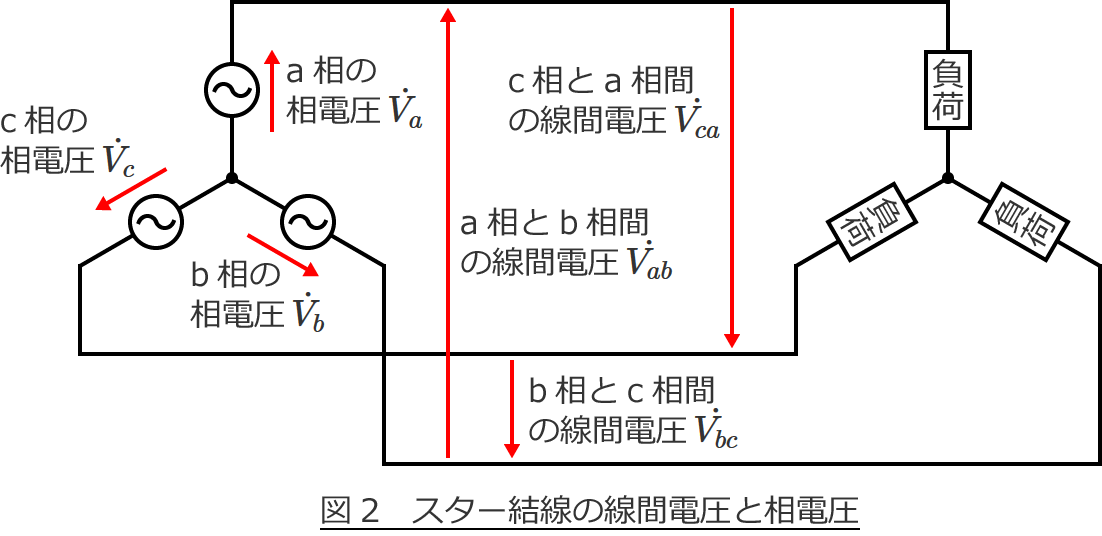
図2　スター結線（Y結線）の線間電圧と相電圧

a相、b相、c相の電源の電圧をそれぞれ $\dot{V_a}$ 、$\dot{V_b}$ 、$\dot{V_c}$ とすると、$\dot{V_a}$ 、$\dot{V_b}$ 、$\dot{V_c}$ それぞれがそのまんま各相の相電圧になって、a相とb相の間にかかる電圧がa相とb相間の線間電圧 $\dot{V_{ab}}$ 、b相とc相の間にかかる電圧がb相とc相間の線間電圧 $\dot{V_{bc}}$ 、c相とa相の間にかかる電圧がc相とa相間の線間電圧 $\dot{V_{ca}}$ になります。

それで、ここでは線間電圧と相電圧の関係を求めたいので、まず初めに図2の回路図の相電圧 $\dot{V_a}$ 、$\dot{V_b}$ 、$\dot{V_c}$ のベクトル図を書いてみると、次のようになります。

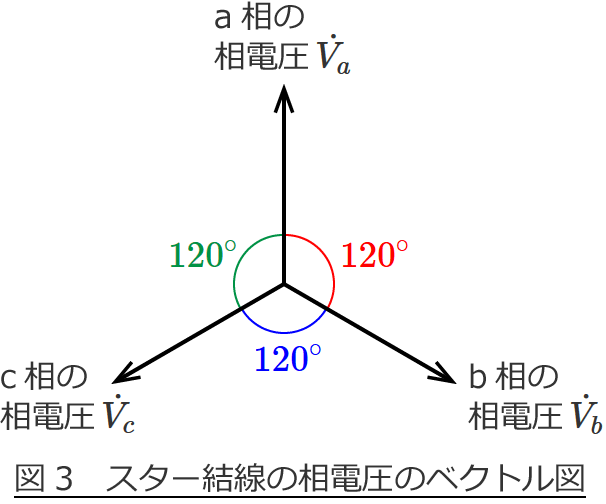
図3　スター結線（Y結線）の相電圧のベクトル図

大きさが同じでa相、b相、c相の位相が $120^\circ$ ずつズレたベクトルになります。（三相電源を対称三相交流電源で考えています。）

相電圧のベクトルが書けたので、あとは線間電圧のベクトルが書ければ相電圧と線間電圧の関係が分かりますね。

線間電圧は、例えばa相とb相間の線間電圧 $\dot{V_{ab}}$ を考える場合、$\dot{V_{ab}}$ はa相の相電圧 $\dot{V_a}$ とb相の相電圧 $\dot{V_b}$ の電位差になるので、2つの相電圧 $\dot{V_a}$ と $\dot{V_b}$ を引き算すると求められます。

直流回路で電位差を求めるときも、ある電圧とある電圧を引き算して電位差を求めますよね？　それと同じ考え方です。

ただしこの場合は、引き算といっても交流なのでベクトルで引き算しないとダメです。

すると線間電圧 $\dot{V_{ab}}$ は、

$\dot{V_{ab}} =\dot{V_a} -\dot{V_b}$　…②　となります。

あとは②のベクトル図を書いてみればいいですね。

図3より、ベクトル $\dot{V_a}$ 、$\dot{V_b}$ だけ書くと次のようになります。

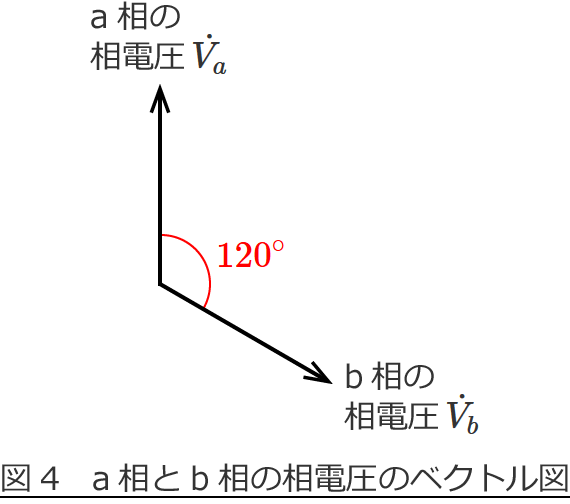
図4　a相とb相の相電圧のベクトル図

書きたいベクトルは $\dot{V_{ab}} =\dot{V_a} -\dot{V_b}$　…② なので、このベクトルの引き算を分かりやすくするために、②式をちょっと変形すると、

$\dot{V_{ab}} =\dot{V_a} +(-\dot{V_b} )$　となります。

この式は、ベクトル $\dot{V_a}$ と $-\dot{V_b}$ を足すとベクトル $\dot{V_{ab}}$ になりますよ、という意味ですね。

ではまず、図4にベクトル $-\dot{V_b}$ を書き加えてみましょう。 $-\dot{V_b}$ は $\dot{V_b}$ と同じ大きさで反対向きのベクトルなので、図5の赤色のベクトルになります。

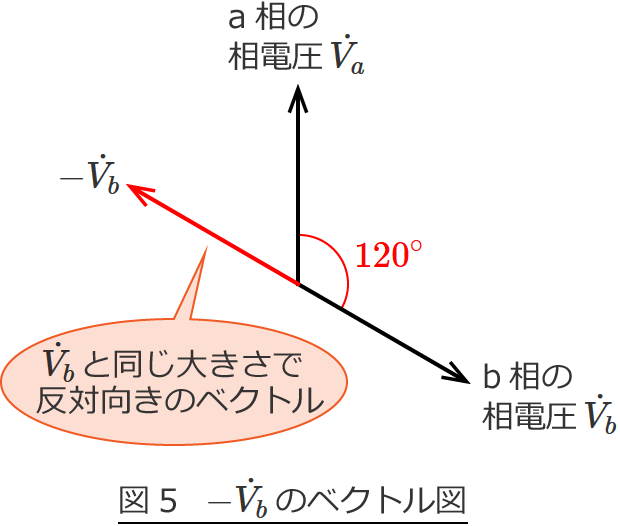
図5　-Vbのベクトル図

あとは、$\dot{V_a}$ と $-\dot{V_b}$ を足せばよく、図6の赤色のベクトルが線間電圧 $\dot{V_{ab}}$ のベクトル図になります。

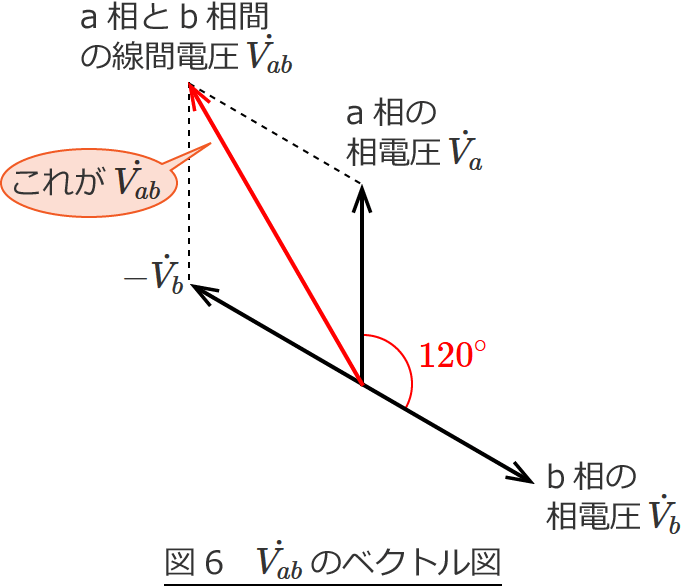
図6　Vabのベクトル図

線間電圧 $\dot{V_{bc}}$ 、$\dot{V_{ca}}$ についても同じように計算すると求められるので、計算は省略してベクトル図を書いてみると次のようになります。

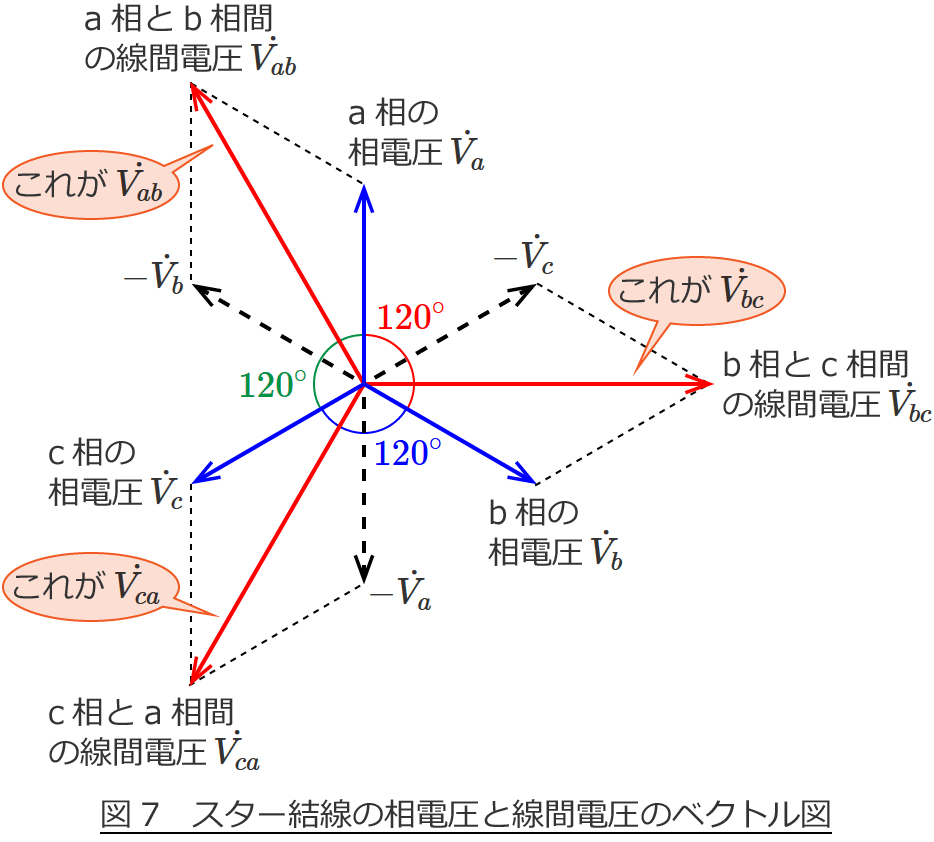
図7　スター結線（Y結線）の相電圧と線間電圧のベクトル図

なんだか急に難しそうになりましたが、線間電圧 $\dot{V_{ab}}$ 、$\dot{V_{bc}}$ 、$\dot{V_{ca}}$ それぞれ分けて考えて、それを一つの図に書いているだけなので、実はそんなに難しくはなかったりします。

ムズイっと思った人は一つ一つ分けて考えてみましょう。

ここまでで相電圧と線間電圧のベクトル図が書けました。それで、ここでの話は、

スター結線の線間電圧はなぜ相電圧の $\sqrt{3}$ 倍になるのか？

なのでした。

図7のベクトル図で解説していくと図がゴチャゴチャになって分かりにくいので、$\dot{V_a}$ と $\dot{V_{ab}}$ のところだけにして角度も書くと次のようになります。

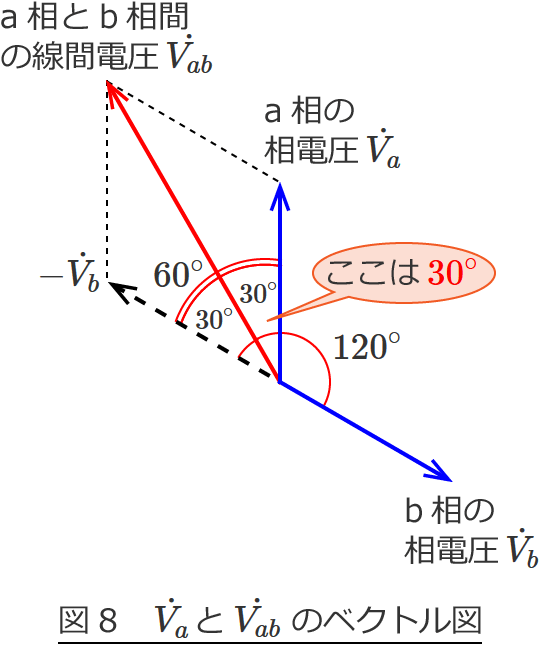
図8　VaとVabのベクトル図

ベクトル $\dot{V_a}$ と $-\dot{V_b}$ の大きさは等しく、2つのベクトルのなす角が $60^\circ$ なので、$\dot{V_a}$ と $\dot{V_{ab}}$ のなす角は $60^\circ$ の半分の $30^\circ$ になります。

図8を $\dot{V_a}$ と $\dot{V_{ab}}$ だけにして、反時計回りにちょっと回転します。

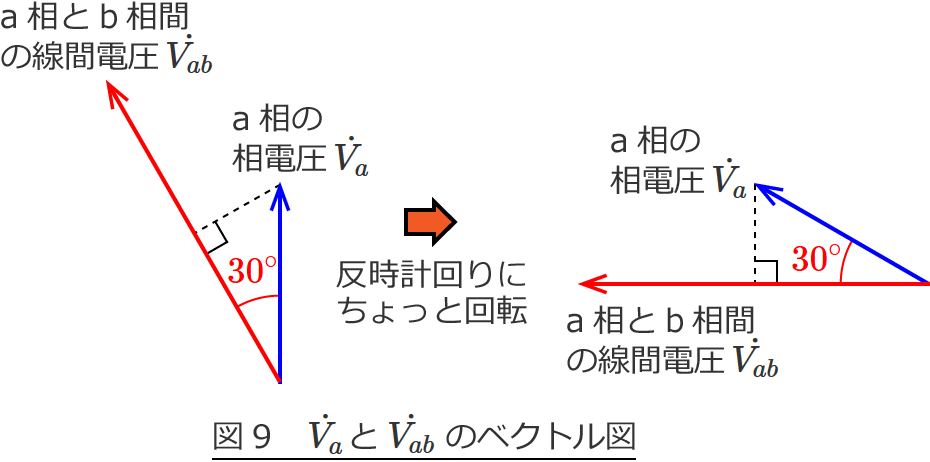
図9　VaとVabのベクトル図

図9の右側の図は元々、4辺の長さが等しい平行四辺形（ひし形）からできている図形です。（ $\because |\dot{V_a} |=|-\dot{V_b} |$ 、$\dot{V_{ab}} =\dot{V_a} +(-\dot{V_b} )$ ）

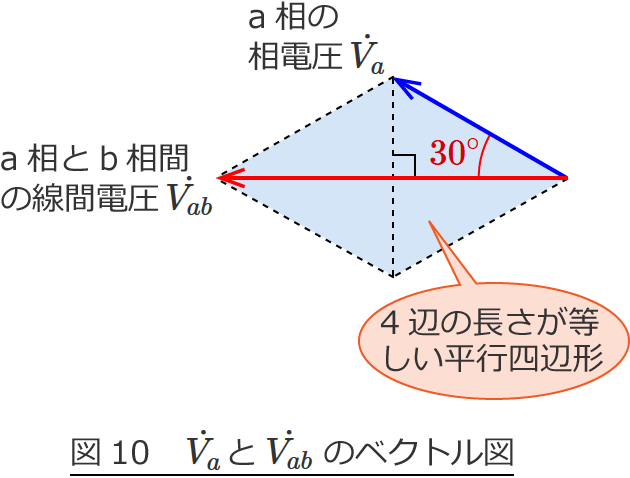
図10　VaとVabのベクトル図

なので、$\dot{V_{ab}}$ の大きさ（長さ）$|\dot{V_{ab}} |$ は $\dot{V_a}$ の大きさ（長さ）$|\dot{V_a} |$ に $\cos 30^\circ$ をかけて2倍すると求められます。式で書けば次のようになります。

$| \dot{V_{ab}} |=|\dot{V_a} |\times\cos 30^\circ\times 2$

$\cos 30^\circ =\dfrac{\sqrt{3}}{2}$ なので、これを代入すると、

$| \dot{V_{ab}} |=|\dot{V_a} |\times\dfrac{\sqrt{3}}{2}\times 2=|\dot{V_a} |\times\sqrt{3}$ $=\sqrt{3}\times |\dot{V_a} |$

$\therefore | \dot{V_{ab}} |=\sqrt{3}\times |\dot{V_a} |$

$| \dot{V_{ab}} |$ は線間電圧の大きさ、$|\dot{V_a} |$ は相電圧の大きさなので、これを言葉で書くと、

線間電圧＝ $\sqrt{3}$ ×相電圧

となり、したがって、スター結線（Y結線）の場合、

線間電圧は相電圧の $\sqrt{3}$ 倍

になる。ということになります。

もちろん、他の相についても同じですよ。

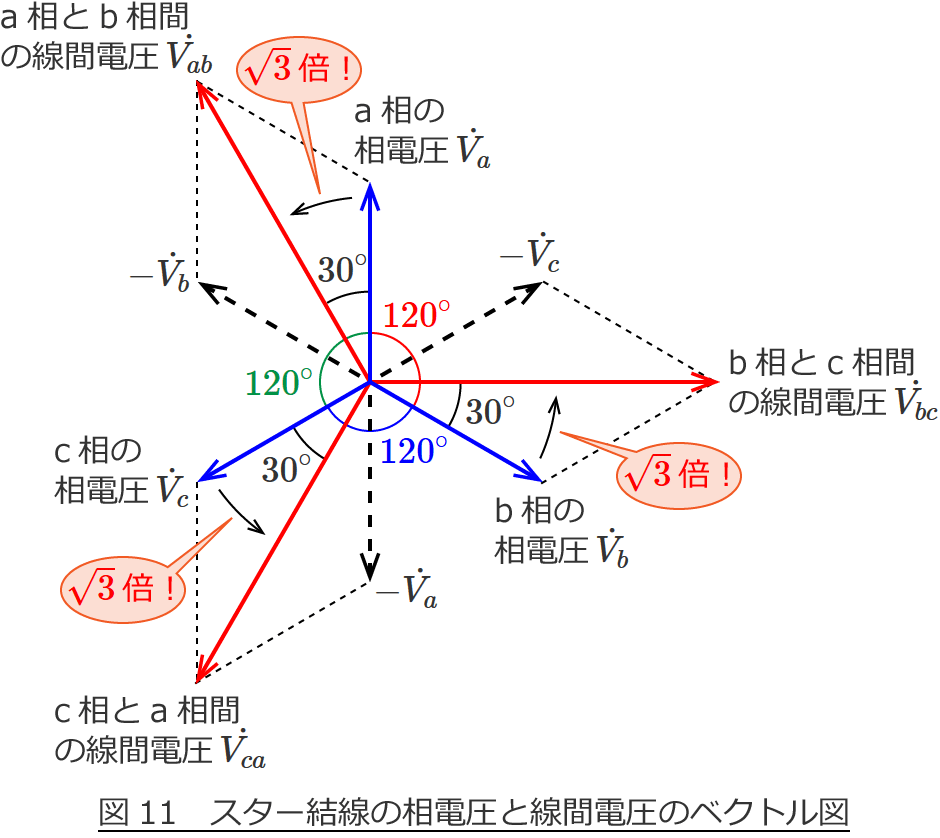
図11　スター結線（Y結線）の相電圧と線間電圧のベクトル図

スター結線（Y結線）の相電圧と線間電圧の関係は、電験三種の「理論」「電力」科目でもよく使われる基本的な公式なので、受験する方は必ずおぼえておくようにしましょう。

三相電力の公式はなぜ√3倍なのか？（三相電力の公式の導出）　←BACK

NEXT→　デルタスター変換（Δ→Y変換）

スター結線（Y結線）の線間電圧はなぜ相電圧の√3倍になるのか？　関連ページ

インピーダンス: インピーダンスについて解説しています。交流回路での電圧と電流の比をインピーダンスといい、インピーダンスの大きさは、交流電流の流れにくさを表わします。インピーダンスの求め方や、インピーダンス三角形、インピーダンス角などについても解説していますので参考にしてみてください。
複素インピーダンス: 複素インピーダンスについて解説しています。複素数で表わされたインピーダンスを複素インピーダンスといい、複素インピーダンスの実部は抵抗、虚部はリアクタンスを表わします。いろいろな交流回路の複素インピーダンスの求め方などについても解説していますので参考にしてみてください。
アドミタンス: アドミタンスについて解説しています。インピーダンスの逆数をアドミタンスといい、アドミタンスの大きさは、交流電流の流れやすさを表わします。アドミタンスの求め方や、アドミタンス三角形、アドミタンス角などについても解説していますので参考にしてみてください。
複素アドミタンス: 複素アドミタンスについて解説しています。複素数で表わされたアドミタンスを複素アドミタンスといい、複素アドミタンスの実部はコンダクタンス、虚部はサセプタンスを表わします。いろいろな交流回路の複素アドミタンスの求め方などについても解説していますので参考にしてみてください。
交流回路のインピーダンスの計算（素子が1個の場合）: 素子（抵抗R、コイルL、コンデンサC）が1個の場合のインピーダンスについて解説しています。素子（R、L、C）が1個なので、計算というほどの計算もなく求められますが、とりあえずインピーダンスの計算の基礎なので・・・。
交流回路の合成インピーダンスの計算（素子が2個直列接続の場合）: 素子（抵抗R、コイルL、コンデンサC）が2個直列接続された場合（RL直列回路、RC直列回路,LC直列回路）の合成インピーダンスを計算しています。LC直列回路の場合には、コイルLとコンデンサCのリアクタンスの大きさによって合成インピーダンスのベクトルの向きが変わるので気を付けましょう。
交流回路の合成インピーダンスの計算（素子が2個並列接続の場合）: 素子（抵抗R、コイルL、コンデンサC）が2個並列接続された場合（RL並列回路、RC並列回路,LC並列回路）の合成インピーダンスを計算しています。LC並列回路の場合は、条件によって合成インピーダンスのベクトルの向きが変わるので気を付けましょう。各合成インピーダンスのベクトル図も書いていますので、参考にしてみてください。
交流回路の合成インピーダンスの計算（RLC直列回路）: 素子（抵抗R、コイルL、コンデンサC）が3個直列接続された場合（RLC直列回路）の合成インピーダンスを計算しています。RLC直列回路の場合、コイルLとコンデンサCのリアクタンスの大きさが同じときには合成インピーダンスは抵抗Rだけになります。これはすごく大事なことなのでおぼえておきましょう！
交流回路の合成インピーダンスの計算（RLC並列回路）: 素子（抵抗R、コイルL、コンデンサC）が3個並列接続された場合（RLC並列回路）の合成インピーダンスを計算しています。RLC並列回路の場合、周波数が反共振周波数のときコイルLとコンデンサCの並列回路部分が解放状態と同じになるため、合成インピーダンスは抵抗Rだけになります。
RLC直列共振回路: RLC直列共振回路について解説しています。RLC直列共振回路はフィルタ回路など電気で幅広く応用されている回路ですので、共振周波数など基本的なことだけでもおぼえておくようにしましょう。
RLC並列共振回路: RLC並列共振回路について解説しています。RLC並列共振回路などの共振回路は電気で幅広く応用されている回路ですので、共振周波数など基本的なことだけでもおぼえておくようにしましょう。
正弦波交流波形の実効値はなぜ最大値÷√2か？: 正弦波交流波形の実効値を求めるときは最大値を√2で割ればいいですが、では、なぜ√2で割れば実効値になるのでしょうか？正弦波交流波形の実効値が最大値÷√2になることを計算で導いてみましたので参考にしてみてください。全波整流波形、半波整流波形、方形波、のこぎり波についても実効値を計算してみました。
なぜコイルに流れる電流の位相は電圧より90°遅れるのか？: コイルに流れる電流の位相は電圧よりも90°遅れますが、コイルの場合、なぜ電流が電圧よりも90°遅れ位相になるのかを計算で導いています。
なぜコンデンサに流れる電流の位相は電圧より90°進むのか？: コンデンサに流れる電流の位相は電圧よりも90°進みますが、コンデンサの場合、なぜ電流が電圧よりも90°進み位相になるのかを計算で導いています。
交流回路の電圧と電流の計算とベクトル図（抵抗だけの回路）: 正弦波交流電源に抵抗だけ接続されている交流回路の回路に流れる電流と、抵抗にかかる電圧の計算方法について解説しています。電圧と電流のベクトル図の描き方についても解説していますので、交流回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（コイルだけの回路）: 正弦波交流電源にコイルだけ接続されている交流回路の回路に流れる電流と、コイルにかかる電圧の計算方法について解説しています。電圧と電流のベクトル図の描き方についても解説していますので、交流回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（コンデンサだけの回路）: 正弦波交流電源にコンデンサだけ接続されている交流回路の回路に流れる電流と、コンデンサにかかる電圧の計算方法について解説しています。電圧と電流のベクトル図の描き方についても解説していますので、交流回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（RL直列回路）: RL直列回路（交流回路）の各素子にかかる電圧、直列接続全体にかかる電圧、位相差の計算方法について解説しています。RL直列回路の電圧と電流のベクトル図の描き方についても解説していますので、RL直列回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（RC直列回路）: RC直列回路（交流回路）の各素子にかかる電圧、直列接続全体にかかる電圧、位相差の計算方法について解説しています。RC直列回路の電圧と電流のベクトル図の描き方についても解説していますので、RC直列回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（RLC直列回路）: RLC直列回路（交流回路）の各素子にかかる電圧、直列接続全体にかかる電圧、位相差の計算方法について解説しています。RLC直列回路の電圧と電流のベクトル図の描き方についても解説していますので、RLC直列回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（RL並列回路）: RL並列回路（交流回路）の各素子に流れる電流、回路全体に流れる電流、位相差の計算方法について解説しています。RL並列回路の電圧と電流のベクトル図の描き方についても解説していますので、RL並列回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（RC並列回路）: RC並列回路（交流回路）の各素子に流れる電流、回路全体に流れる電流、位相差の計算方法について解説しています。RC並列回路の電圧と電流のベクトル図の描き方についても解説していますので、RC並列回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（LC並列回路）: LC並列回路（交流回路）の各素子に流れる電流と、回路全体に流れる電流の計算方法について解説しています。LC並列回路の電圧と電流のベクトル図の描き方についても解説していますので、LC並列回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（RLC並列回路）: RLC並列回路（交流回路）の各素子に流れる電流、回路全体に流れる電流、位相差の計算方法について解説しています。RLC並列回路の電圧と電流のベクトル図の描き方についても解説していますので、RLC並列回路の計算やベクトル図の描き方の参考にしてみてください。
RL直列回路の電圧と電流の計算（電源の電圧を基準にした場合）: RL直列回路の回路に流れる電流と各素子にかかる電圧を電源の電圧を基準にして計算していますので、RL直列回路の電圧と電流の計算方法の参考にしてみてください。
RC直列回路の電圧と電流の計算（電源の電圧を基準にした場合）: RC直列回路の回路に流れる電流と各素子にかかる電圧を電源の電圧を基準にして計算していますので、RC直列回路の電圧と電流の計算方法の参考にしてみてください。
RLC直列回路の電圧と電流の計算（電源の電圧を基準にした場合）: RLC直列回路の回路に流れる電流と各素子にかかる電圧を電源の電圧を基準にして計算していますので、RLC直列回路の電圧と電流の計算方法の参考にしてみてください。
交流回路の電力の計算（抵抗だけの回路）: 負荷が抵抗だけの場合の交流回路の電力（瞬時電力、平均電力）の計算方法（求め方）、電力の波形などについて解説しています。
交流回路の電力の計算（コイルだけの回路）: 負荷がコイルだけの場合の交流回路の電力（瞬時電力、平均電力）の計算方法（求め方）、電力の波形などについて解説しています。
交流回路の電力の計算（コンデンサだけの回路）: 負荷がコンデンサだけの場合の交流回路の電力（瞬時電力、平均電力）の計算方法（求め方）、電力の波形などについて解説しています。
交流回路の電力の計算（RL直列回路）: RL直列回路の電力（瞬時電力、平均電力）の計算方法（求め方）、電力の波形などについて解説しています。
交流回路の電力の計算（RC直列回路）: RC直列回路の電力（瞬時電力、平均電力）の計算方法（求め方）、電力の波形などについて解説しています。
有効・無効・皮相電力: 交流回路には「有効電力」「無効電力」「皮相電力」の3種類の電力があります。それぞれの電力の求め方と、3つの電力の関係について解説しています。
力率とは？（力率と電力の関係）: 交流回路の勉強をしていると「力率」がでてきますが、力率って何でしょうか？力率の式の表し方には色々ありますが、ここでは、力率と皮相電力、有効電力、無効電力の関係とその関係式などについて解説します。
力率とは？（力率と位相の関係）: 交流回路の勉強をしていると「力率(cosΘ)」がでてきますが、力率って何でしょうか？力率の式の表し方には色々ありますが、ここでは、位相と力率の関係について抵抗、コイル、コンデンサの回路を例に解説しています。
波形の実効値、平均値、最大値、波形率、波高率の求め方: 波形は色々ありますが、その波形の特性を表わす値として実効値、平均値、最大値、波形率、波高率などがあります。ここでは、波形の実効値、平均値、最大値、波形率、波高率の定義式、求め方について解説しています。
正弦波波形の実効値、平均値、最大値、波形率、波高率の計算方法: 波形は色々ありますが、その波形の特性を表わす値として実効値、平均値、最大値、波形率、波高率などがあります。ここでは、正弦波波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。
全波整流波形の実効値、平均値、最大値、波形率、波高率の計算方法: 波形は色々ありますが、その波形の特性を表わす値として実効値、平均値、最大値、波形率、波高率などがあります。ここでは、全波整流波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。
半波整流波形の実効値、平均値、最大値、波形率、波高率の計算方法: 半波整流波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。波形の特性を表わす値として実効値、平均値、最大値、波形率、波高率などがありますが、これらは大事な値ですので、求め方、計算方法をおぼえておきましょう。
方形波波形の実効値、平均値、最大値、波形率、波高率の計算方法: 方形波波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。方形波波形の場合、実効値と平均値と最大値が同じ値、波形率と波高率が同じ値になります。ちなみに、方形波と矩形波は同じです。
のこぎり波波形の実効値、平均値、最大値、波形率、波高率の計算方法: のこぎり波波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。のこぎり波波形の実効値と平均値を求めるためには、のこぎり波波形の式から考えないといけないので、他の波形よりも計算がちょっと大変です。
三相電力の公式はなぜ√3倍なのか？（三相電力の公式の導出）: 三相電力の公式はP＝√3VIcosφで表わされますが、なぜ√3倍になるのか？スター結線の場合とデルタ結線の場合それぞれについて、三相電力の公式を導出してみました。この三相電力の公式は電験三種の「理論」「電力」科目の問題を解くときに度々使われる基本的な公式ですのでおぼえておくようにしましょう。
デルタスター変換（Δ→Y変換）: デルタスター変換（Δ→Y変換）について解説しています。デルタ結線（Δ結線）を等価なスター結線（Y結線）に変換するのをデルタスター変換（Δ→Y変換）といいます。デルタスター変換の式の導出方法についても解説していますので参考にしてみてください。
スターデルタ変換（Y→Δ変換）: スターデルタ変換（Y→Δ変換）について解説しています。スター結線（Y結線）を等価なデルタ結線（Δ結線）に変換するのをスターデルタ変換（Y→Δ変換）といいます。スターデルタ変換の式の導出方法についても解説していますので参考にしてみてください。
交流回路のテブナンの定理: 交流回路のテブナンの定理（鳳-テブナンの定理）について解説しています。テブナンの定理を使った交流回路の計算方法や、交流回路のテブナンの定理の証明についても解説していますので参考にしてみてください。

交流回路｜スター結線（Y結線）の線間電圧はなぜ相電圧の√3倍になるのか？