ƒXƒ|ƒ“ƒTپ[ƒٹƒ“ƒN
Œً—¬‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جŒvژZپi‘fژq‚ھ2Œآ•ہ—ٌگع‘±‚جڈêچ‡پj
پ¦ƒyپ[ƒW“à‚ةPR¥چLچگ‚ھٹـ‚ـ‚ê‚éڈêچ‡‚ھ‚ ‚è‚ـ‚·پB
‰ٌکH‚ج‘fژqپi’ïچR $R$ پAƒRƒCƒ‹ $L$ پAƒRƒ“ƒfƒ“ƒT $C$ پj‚ھ2Œآ•ہ—ٌگع‘±‚³‚ê‚ؤ‚¢‚éڈêچ‡‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ًŒvژZ‚µ‚ؤ‚ف‚ـ‚·پB
’ïچRR‚ئƒRƒCƒ‹L‚ج•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒXپiRL•ہ—ٌ‰ٌکHپj
RL•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX
RL•ہ—ٌ‰ٌکH‚حپA’ïچR $R$ ‚ئƒRƒCƒ‹ $L$ ‚ھ•ہ—ٌ‚ةگع‘±‚³‚ꂽ‰ٌکH‚إپAژں‚ج‚و‚¤‚ب‰ٌکH‚ة‚ب‚è‚ـ‚·پB
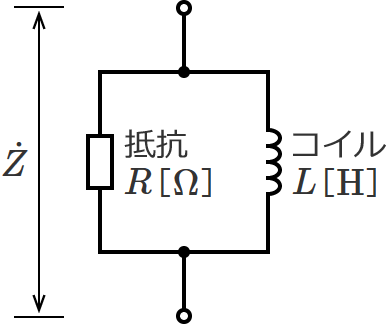
•ہ—ٌگع‘±‚ب‚ج‚إپA‚±‚ج‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚حپA
‚»‚ꂼ‚ê‚جƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‹tگ”پ¦‚ً‘«‚µ‚ؤپA‚»‚ê‚ج‹tگ”‚ً‚ئ‚ê‚خ
‹پ‚ك‚ç‚ê‚ـ‚·پB
ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‹tگ”‚ًƒAƒhƒ~ƒ^ƒ“ƒX‚ئ‚¢‚¢‚ـ‚·پB
‚±‚جŒvژZ•û–@‚ء‚ؤپA•ہ—ٌگع‘±‚³‚ꂽ’ïچR‚جچ‡گ¬’ïچR‚ً‹پ‚ك‚é‚ئ‚«‚ئ“¯‚¶‚â‚è•û‚ب‚ٌ‚إ‚·‚و‚ثپBپiچ‡گ¬’ïچR‚جڈêچ‡پA’ïچR‚ج‹tگ”‚ً‘«‚µ‚ؤپA‚»‚ê‚ً‹tگ”‚ة‚·‚éپB‚ف‚½‚¢‚بپBپj
‚؟‚ه‚ء‚ئکb‚ح‚»‚ê‚ـ‚·‚ھپAژں‚ج‚و‚¤‚ة2‚آ‚ج’ïچR‚ھ•ہ—ٌ‚ةگع‘±‚³‚ꂽ‰ٌکH‚ھ‚ ‚é‚ئ‚µ‚ـ‚·پB
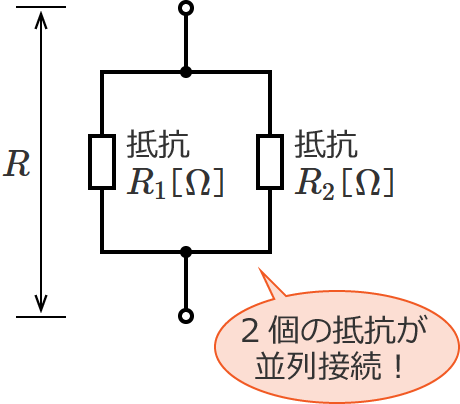
‚·‚é‚ئپA‚±‚ج‰ٌکH‚جچ‡گ¬’ïچR $R$ ‚ء‚ؤپAژں‚ج‚و‚¤‚ة‹پ‚ك‚ـ‚·‚و‚ثپH
$\dfrac{1}{R} = \dfrac{1}{R_1} + \dfrac{1}{R_2}$پ@پc①پ@پ@$\dfrac{1}{R} = \dfrac{R_2 + R_1}{R_1 R_2}$
•ھ•ê‚ئ•ھژq‚ً‚ذ‚ء‚‚è•ش‚µ‚ؤپAپ@$\therefore R = \dfrac{R_1 R_2}{R_1 + R_2}$پ@پiپ©چ‡گ¬’ïچR‚ھ‹پ‚ك‚ç‚ꂽپj
‚±‚ج‚â‚è•û‚ئ“¯‚¶‚و‚¤‚ة‚·‚é‚ئپA•ہ—ٌگع‘±‚ج‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ً‹پ‚ك‚邱‚ئ‚ھ‚إ‚«‚ـ‚·پB
‚ب‚ج‚إپARL•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚حپA①ژ®‚ئ“¯‚¶‚و‚¤‚بژں‚جژ®‚إ—^‚¦‚ç‚ê‚ـ‚·پBپi $\omega$ ‚حٹpژü”gگ”پi $\omega = 2 \pi f$ پj‚إ‚·پBپj

‚ ‚ئ‚ح‚±‚جژ®‚ًگ®—‚µ‚ؤپA$\dot{Z} = \cdots$ ‚ة‚·‚ê‚خچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ً‹پ‚ك‚邱‚ئ‚ھ‚إ‚«‚ـ‚·پB
$\dfrac{1}{\dot{Z}} = \dfrac{j \omega L + R}{R \cdot j \omega L} = \dfrac{R + j \omega L}{j \omega R L}$
•ھ•ê‚ئ•ھژq‚ً‚ذ‚ء‚‚è•ش‚µ‚ؤپAپ@$\dot{Z} = \dfrac{j \omega R L}{R + j \omega L}$
‚±‚جژ®‚ً‹•گ”’Pˆت $j$ ‚إگ®—‚µ‚½‚¢‚ج‚إپA•ھ•ê‚ئ•ھژq‚ة $\left( R - j \omega L \right)$ ‚ً‚©‚¯‚é‚ئپA
$\dot{Z} = \dfrac{j \omega R L \left( R - j \omega L \right)}{\left( R + j \omega L \right) \left( R - j \omega L \right)}$ $= \dfrac{j \omega R^2 L - j \omega R L \cdot j \omega L}{R^2 - j \omega R L + j \omega R L - \left( j \omega L \right)^2}$ $= \dfrac{j \omega R^2 L - j^2 \omega^2 R L^2}{R^2 - \left( j \omega L \right)^2}$
$= \dfrac{j \omega R^2 L + \omega^2 R L^2}{R^2 - j^2 \omega^2 L^2}$ $= \dfrac{\omega^2 R L^2 + j \omega R^2 L}{R^2 + \omega^2 L^2}$ $= \dfrac{\omega^2 R L^2}{R^2 + \omega^2 L^2} + j \dfrac{\omega R^2 L}{R^2 + \omega^2 L^2}$
‚µ‚½‚ھ‚ء‚ؤپARL•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚حپA
$\therefore \dot{Z} = \dfrac{\omega^2 R L^2}{R^2 + \omega^2 L^2} + j \dfrac{\omega R^2 L}{R^2 + \omega^2 L^2}$پ@پm$ \mathrm{\Omega} $پnپ@پc②
‚ئ‚ب‚è‚ـ‚·پB‚؟‚ه‚ء‚ئ‚â‚₱‚µ‚¢ژ®‚ة‚ب‚è‚ـ‚µ‚½‚ثپB
RL•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‘ه‚«‚³
RL•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚ج‘ه‚«‚³‚حپA②ژ®‚جگâ‘خ’l‚ً‹پ‚ك‚ê‚خ‚¢‚¢‚ج‚إپA
$| \dot{Z} |$ $= \sqrt{\left( \dfrac{\omega^2 R L^2}{R^2 + \omega^2 L^2} \right)^2 + \left( \dfrac{\omega R^2 L}{R^2 + \omega^2 L^2} \right)^2}$ $= \sqrt{\dfrac{\omega^4 R^2 L^4 + \omega^2 R^4 L^2}{\left( R^2 + \omega^2 L^2 \right)^2}}$
$= \sqrt{\dfrac{\omega^2 R^2 L^2 \left( \omega^2 L^2 + R^2 \right)}{\left( R^2 + \omega^2 L^2 \right)^2}}$ $= \sqrt{\dfrac{\omega^2 R^2 L^2}{R^2 + \omega^2 L^2}}$ $= \dfrac{\omega R L}{\sqrt{R^2 + \omega^2 L^2}}$
$\therefore| \dot{Z} | = \dfrac{\omega R L}{\sqrt{R^2 + \omega^2 L^2}}$پ@پm$ \mathrm{\Omega} $پn
‚ئ‚ب‚è‚ـ‚·پB
RL•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جƒxƒNƒgƒ‹گ}
RL•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚جƒxƒNƒgƒ‹گ}‚حپAچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ھ $\dot{Z} = \dfrac{\omega^2 R L^2}{R^2 + \omega^2 L^2} + j \dfrac{\omega R^2 L}{R^2 + \omega^2 L^2}$ ‚ب‚ج‚إپAژں‚ج‚و‚¤‚ة‚ب‚è‚ـ‚·پB
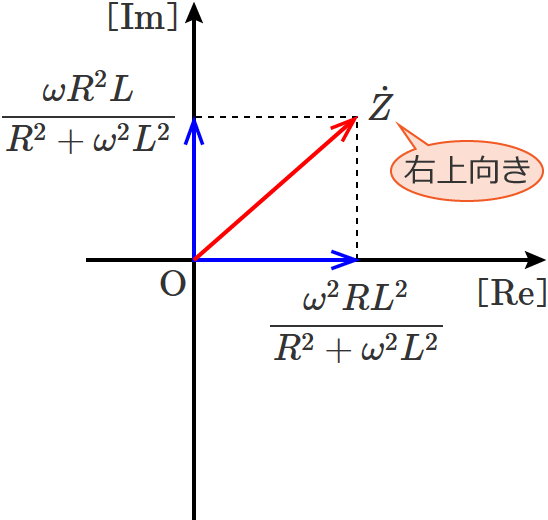
$\omega \gt 0$ پA$R \gt 0$ پA$L \gt 0$ ‚ب‚ج‚إپA$\dot{Z}$ ‚جژہ•” $= \dfrac{\omega^2 R L^2}{R^2 + \omega^2 L^2} \gt 0$ پA$\dot{Z}$ ‚ج‹••” $= \dfrac{\omega R^2 L}{R^2 + \omega^2 L^2} \gt 0$ ‚ئ‚ب‚èپAچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚جƒxƒNƒgƒ‹پiڈمگ}‚جگشگF‚جƒxƒNƒgƒ‹پj‚جŒü‚«‚ح•K‚¸‰EڈمŒü‚«‚ة‚ب‚è‚ـ‚·پB
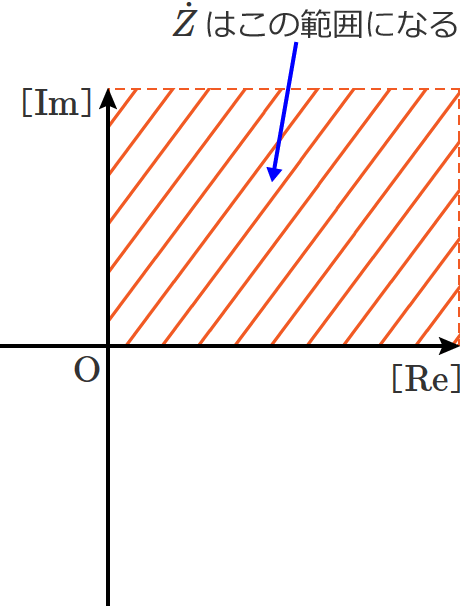
ƒOƒ‰ƒt‚ج‰،ژ²‚ئڈcژ²‚ة‚آ‚¢‚ؤ
ƒOƒ‰ƒt‚ج‰،ژ²‚ئڈcژ²‚ةڈ‘‚¢‚ؤ‚ ‚éپm$\mathrm{Re}$پn‚ئپm$\mathrm{Im}$پn‚حپA•،‘f•½–ت‚جژہژ²‚ئ‹•ژ²‚ئ‚¢‚¤ˆس–،‚إ‚·پB•،‘f•½–ت‚جژہژ²‚ة‚ح•،‘fگ”‚جژہ•”‚ھ‘خ‰‚µپA‹•ژ²‚ة‚ح•،‘fگ”‚ج‹••”‚ھ‘خ‰‚µ‚ـ‚·پB
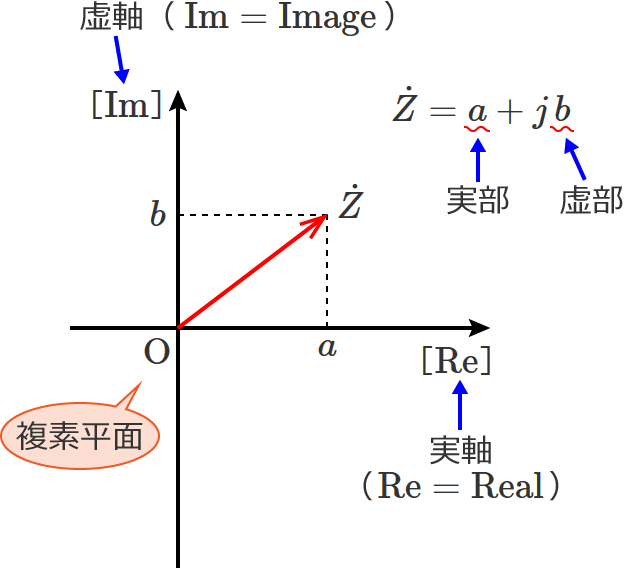
‚؟‚ب‚ف‚ةپA•،‘f•½–ت‚حپAƒKƒEƒX•½–ت‚ئ‚©•،‘fگ”•½–ت‚ئ‚à‚¢‚¢‚ـ‚·پB
کa•ھ‚جگد‚إچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒXپH
•ہ—ٌگع‘±‚³‚ꂽ2‚آ‚ج’ïچR‚جچ‡گ¬’ïچR‚ً‹پ‚ك‚é‚ئ‚«‚ةپA‚و‚کa•ھ‚جگد‚جŒِژ®‚ھژg‚ي‚ê‚ـ‚·‚ھپARL•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ً‹پ‚ك‚é‚ئ‚«‚à“¯‚¶‚و‚¤‚ةکa•ھ‚جگد‚ًژg‚¤‚±‚ئ‚ھ‚إ‚«‚ـ‚·پBپi‘fژq‚ھ3‚آˆبڈم‚ج‚ئ‚«‚حکa•ھ‚جگد‚µ‚؟‚لƒ_ƒپ‚إ‚·‚وپIپj
’ïچR $R$ ‚ئƒRƒCƒ‹ $L$ ‚جƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ً‚»‚ꂼ‚ê $R$پm$ \mathrm{\Omega} $پnپA$j \omega L$پm$ \mathrm{\Omega} $پn‚ئ‚µپA‚±‚ج2‚آ‚إکa•ھ‚جگد‚µ‚ؤ‚ف‚é‚ئپA
$\dfrac{R \times j \omega L}{R + j \omega L}$ $= \dfrac{j \omega R L \left( R - j \omega L \right)}{\left( R + j \omega L \right) \left( R - j \omega L \right)}$ $= \dfrac{j \omega R^2 L + \omega^2 R L^2}{R^2 + \omega^2 L^2}$ $= \dfrac{\omega^2 R L^2}{R^2 + \omega^2 L^2} + j \dfrac{\omega R^2 L}{R^2 + \omega^2 L^2}$
$\therefore \dfrac{R \times j \omega L}{R + j \omega L}$ $= \dfrac{\omega^2 R L^2}{R^2 + \omega^2 L^2} + j \dfrac{\omega R^2 L}{R^2 + \omega^2 L^2}$پ@پc③
‚ئ‚ب‚è‚ـ‚·پB‚ثپHپ@②‚ئ③‚ح“™‚µ‚‚ب‚ء‚ؤ‚¢‚ـ‚·‚و‚ثپB
ƒXƒ|ƒ“ƒTپ[ƒٹƒ“ƒN
’ïچRR‚ئƒRƒ“ƒfƒ“ƒTC‚ج•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒXپiRC•ہ—ٌ‰ٌکHپj
RC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX
RC•ہ—ٌ‰ٌکH‚حپA’ïچR $R$ ‚ئƒRƒ“ƒfƒ“ƒT $C$ ‚ھ•ہ—ٌ‚ةگع‘±‚³‚ꂽ‰ٌکH‚إپAژں‚ج‚و‚¤‚ب‰ٌکH‚ة‚ب‚è‚ـ‚·پB
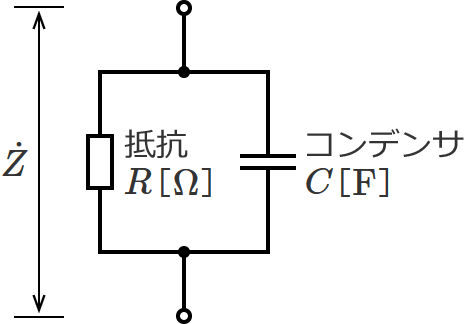
•ہ—ٌگع‘±‚ب‚ج‚إپA‚±‚ج‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚àپA
‚»‚ꂼ‚ê‚جƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‹tگ”پ¦‚ً‘«‚µ‚ؤپA‚»‚ê‚ج‹tگ”‚ً‚ئ‚ê‚خ
‹پ‚ك‚ç‚ê‚ـ‚·پB
ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‹tگ”‚ًƒAƒhƒ~ƒ^ƒ“ƒX‚ئ‚¢‚¢‚ـ‚·پB
‚µ‚½‚ھ‚ء‚ؤپA’ïچR $R$ ‚جƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‹tگ”‚ح $\dfrac{1}{R}$ پAƒRƒ“ƒfƒ“ƒT $C$ ‚جƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‹tگ”‚ح $j \omega C$ ‚ب‚ج‚إپARC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚حژں‚جژ®‚إ—^‚¦‚ç‚ê‚ـ‚·پB
$\dfrac{1}{\dot{Z}} = \dfrac{1}{R} + j \omega C$
‚ ‚ئ‚ح‚±‚جژ®‚ًگ®—‚µ‚ؤپA$\dot{Z} = \cdots$ ‚ة‚·‚ê‚خچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ً‹پ‚ك‚邱‚ئ‚ھ‚إ‚«‚ـ‚·پB
$\dfrac{1}{\dot{Z}} = \dfrac{1}{R} + j \omega C = \dfrac{1 + j \omega R C}{R}$
•ھ•ê‚ئ•ھژq‚ً‚ذ‚ء‚‚è•ش‚µ‚ؤپAپ@$\dot{Z} = \dfrac{R}{1 + j \omega R C}$
‚±‚جژ®‚ً‹•گ”’Pˆت $j$ ‚إگ®—‚µ‚½‚¢‚ج‚إپA•ھ•ê‚ئ•ھژq‚ة $\left( 1 - j \omega R C \right)$ ‚ً‚©‚¯‚é‚ئپA
$\dot{Z} = \dfrac{R \left( 1 - j \omega R C \right)}{\left( 1 + j \omega R C \right) \left( 1 - j \omega R C \right)}$ $= \dfrac{R - j \omega R^2 C}{1 - j \omega R C + j \omega R C - \left( j \omega R C \right)^2}$
$= \dfrac{R - j \omega R^2 C}{1 - j^2 \omega^2 R^2 C^2}$ $= \dfrac{R - j \omega R^2 C}{1 + \omega^2 R^2 C^2}$ $= \dfrac{R}{1 + \omega^2 R^2 C^2} - j \dfrac{\omega R^2 C}{1 + \omega^2 R^2 C^2}$
‚µ‚½‚ھ‚ء‚ؤپARC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚حپA
$\therefore \dot{Z} = \dfrac{R}{1 + \omega^2 R^2 C^2} - j \dfrac{\omega R^2 C}{1 + \omega^2 R^2 C^2}$پ@پm$ \mathrm{\Omega} $پnپ@پc④
‚ئ‚ب‚è‚ـ‚·پB
RC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‘ه‚«‚³
RC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚ج‘ه‚«‚³‚حپA④ژ®‚جگâ‘خ’l‚ً‹پ‚ك‚ê‚خ‚¢‚¢‚ج‚إپA
$| \dot{Z} |$ $= \sqrt{\left( \dfrac{R}{1 + \omega^2 R^2 C^2} \right)^2 + \left( \dfrac{\omega R^2 C}{1 + \omega^2 R^2 C^2} \right)^2}$ $= \sqrt{\dfrac{R^2 + \omega^2 R^4 C^2}{\left( 1 + \omega^2 R^2 C^2 \right)^2}}$
$= \sqrt{\dfrac{R^2 \left( 1 + \omega^2 R^2 C^2 \right)}{\left( 1+ \omega^2 R^2 C^2 \right)^2}}$ $= \sqrt{\dfrac{R^2}{1 + \omega^2 R^2 C^2}}$ $= \dfrac{R}{\sqrt{1 + \omega^2 R^2 C^2}}$
$\therefore | \dot{Z} | = \dfrac{R}{\sqrt{1 + \omega^2 R^2 C^2}}$پ@پm$ \mathrm{\Omega} $پn
‚ئ‚ب‚è‚ـ‚·پB
RC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جƒxƒNƒgƒ‹گ}
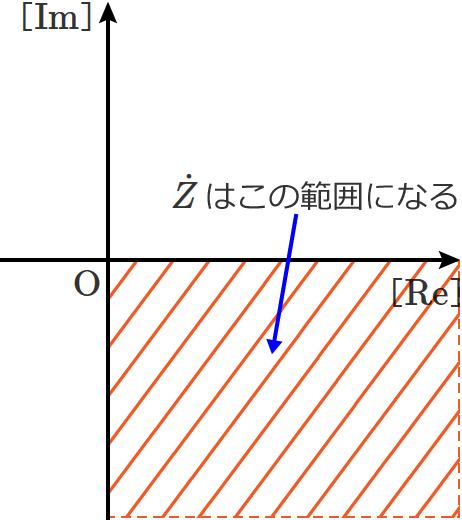
RC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚جƒxƒNƒgƒ‹گ}‚حپAچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ھ $\dot{Z} = \dfrac{R}{1 + \omega^2 R^2 C^2} - j \dfrac{\omega R^2 C}{1 + \omega^2 R^2 C^2}$ ‚ب‚ج‚إپAژں‚ج‚و‚¤‚ة‚ب‚è‚ـ‚·پB
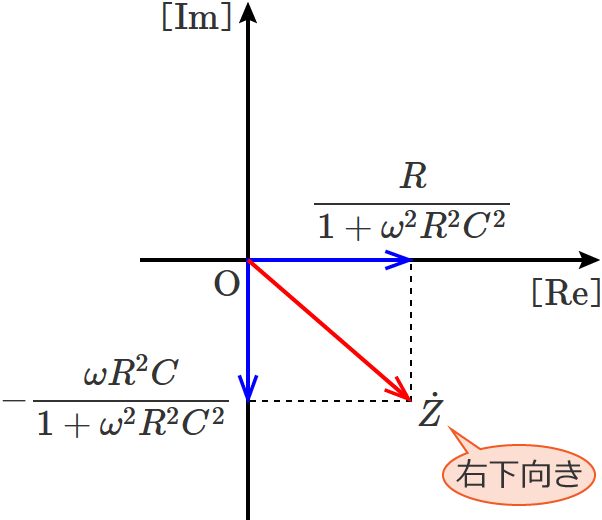
$\omega \gt 0$ پA$R \gt 0$ پA$C \gt 0$ ‚ب‚ج‚إپA$\dot{Z}$ ‚جژہ•” $= \dfrac{R}{1 + \omega^2 R^2 C^2} \gt 0$ پA$\dot{Z}$ ‚ج‹••” $= -\dfrac{\omega R^2 C}{1 + \omega^2 R^2 C^2} \lt 0$ ‚ئ‚ب‚èپAچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚جƒxƒNƒgƒ‹پiڈمگ}‚جگشگF‚جƒxƒNƒgƒ‹پj‚جŒü‚«‚ح•K‚¸‰E‰؛Œü‚«‚ة‚ب‚è‚ـ‚·پB
ƒXƒ|ƒ“ƒTپ[ƒٹƒ“ƒN
ƒXƒ|ƒ“ƒTپ[ƒٹƒ“ƒN
ƒRƒCƒ‹L‚ئƒRƒ“ƒfƒ“ƒTC‚ج•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒXپiLC•ہ—ٌ‰ٌکHپj
LC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX
LC•ہ—ٌ‰ٌکH‚حپAƒRƒCƒ‹ $L$ ‚ئƒRƒ“ƒfƒ“ƒT $C$ ‚ھ•ہ—ٌ‚ةگع‘±‚³‚ꂽ‰ٌکH‚إپAژں‚ج‚و‚¤‚ب‰ٌکH‚ة‚ب‚è‚ـ‚·پB
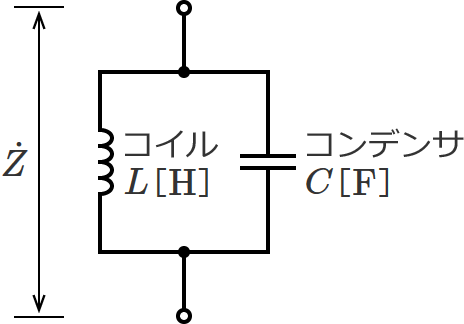
•ہ—ٌگع‘±‚ب‚ج‚إپA‚±‚ج‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚àپA
‚»‚ꂼ‚ê‚جƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‹tگ”پ¦‚ً‘«‚µ‚ؤپA‚»‚ê‚ج‹tگ”‚ً‚ئ‚ê‚خ
‹پ‚ك‚ç‚ê‚ـ‚·پB
ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‹tگ”‚ًƒAƒhƒ~ƒ^ƒ“ƒX‚ئ‚¢‚¢‚ـ‚·پB
‚µ‚½‚ھ‚ء‚ؤپAƒRƒCƒ‹ $L$ ‚جƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‹tگ”‚ح $\dfrac{1}{j \omega L}$ پAƒRƒ“ƒfƒ“ƒT $C$ ‚جƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‹tگ”‚ح $j \omega C$ ‚ب‚ج‚إپALC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚حژں‚جژ®‚إ—^‚¦‚ç‚ê‚ـ‚·پB
$\dfrac{1}{\dot{Z}} = \dfrac{1}{j \omega L} + j \omega C$
‚ ‚ئ‚ح‚±‚جژ®‚ًگ®—‚µ‚ؤپA$\dot{Z} = \cdots$ ‚ة‚·‚ê‚خچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ً‹پ‚ك‚邱‚ئ‚ھ‚إ‚«‚ـ‚·پB
$\dfrac{1}{\dot{Z}} = \dfrac{1}{j \omega L} + j \omega C$ $= \dfrac{1 + j \omega C \cdot j \omega L}{j \omega L}$ $= \dfrac{1 + j^2 \omega^2 L C}{j \omega L}$ $= \dfrac{1 - \omega^2 L C}{j \omega L}$
•ھ•ê‚ئ•ھژq‚ً‚ذ‚ء‚‚è•ش‚µ‚ؤپAپ@$\dot{Z} = \dfrac{j \omega L}{1 - \omega^2 L C} = j \dfrac{\omega L}{1 - \omega^2 L C}$
‚µ‚½‚ھ‚ء‚ؤپALC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚حپA
$\therefore \dot{Z} = j \dfrac{\omega L}{1 - \omega^2 L C}$پ@پm$ \mathrm{\Omega} $پnپ@پc⑤
‚ئ‚ب‚è‚ـ‚·پB
LC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‘ه‚«‚³
LC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚ج‘ه‚«‚³‚حپA⑤ژ®‚جگâ‘خ’l‚ً‹پ‚ك‚ê‚خ‚¢‚¢‚ج‚إپA
$| \dot{Z} | = \sqrt{\left( \dfrac{\omega L}{1 - \omega^2 L C} \right)^2}$ $= \left| \dfrac{\omega L}{1 - \omega^2 L C} \right|$
$\therefore | \dot{Z} | = \left| \dfrac{\omega L}{1 - \omega^2 L C} \right|$پ@پm$ \mathrm{\Omega} $پn
‚ئ‚ب‚è‚ـ‚·پB
LC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جƒxƒNƒgƒ‹گ}
LC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚جƒxƒNƒgƒ‹گ}‚ًڈ‘‚‚ئ‚«‚حپA⑤ژ®‚ج•ھ•ê‚ھگ³‚ة‚ب‚é‚©پH•‰‚ة‚ب‚é‚©پH‚ـ‚½‚حƒ[ƒچ‚ة‚ب‚é‚©پH‚ة‚و‚ء‚ؤچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚جƒxƒNƒgƒ‹‚جŒü‚«‚ھ•د‚ي‚é‚ج‚إپA‚؟‚ه‚ء‚ئ’چˆس‚ھ•K—v‚إ‚·‚وپBپi$\omega \gt 0$ پA$L \gt 0$ ‚ب‚ج‚إپA•ھژq‚ج $\omega L$ ‚حڈي‚ةگ³‚ة‚ب‚é‚ج‚إ•ھژq‚ة‚آ‚¢‚ؤ‚حچl‚¦‚ب‚‚ؤ‚¢‚¢‚إ‚·پBپj
‚آ‚ـ‚èپA$1 - \omega^2 L C \gt 0$ ‚ج‚ئ‚«پA$1 - \omega^2 L C \lt 0$ ‚ج‚ئ‚«پA$1 - \omega^2 L C = 0$ ‚ج‚ئ‚«‚إپAڈêچ‡•ھ‚¯‚µ‚ؤچl‚¦‚ب‚¯‚ê‚خ‚ب‚ç‚ب‚¢‚ئ‚¢‚¤‚±‚ئ‚إ‚·پB‚؟‚ه‚ء‚ئ‚ك‚ٌ‚ا‚‚³‚¢‚إ‚·‚ثپB
پi$\mathrm{A}$پj$1 - \omega^2 L C \gt 0$ ‚ج‚ئ‚«
$1 - \omega^2 L C \gt 0$ ‚ج‚ئ‚«‚ح‡Dژ®‚ج $j$ ‚ة‚©‚©‚é’l‚ھگ³‚ئ‚¢‚¤‚±‚ئ‚ة‚ب‚é‚ج‚إپAچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚جƒxƒNƒgƒ‹‚حپAژں‚ج‚و‚¤‚ةڈمŒü‚«‚ة‚ب‚è‚ـ‚·پB
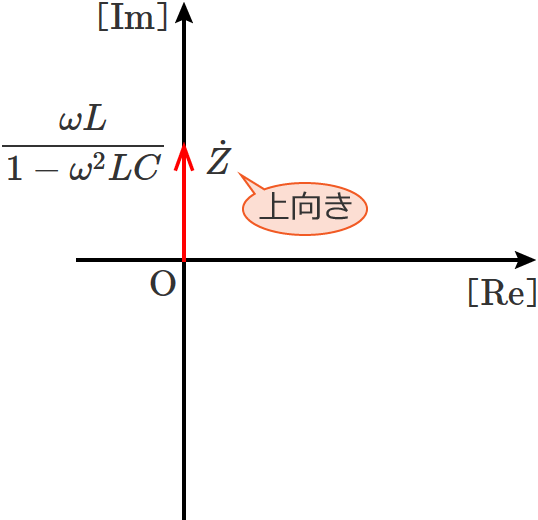
پi$\mathrm{B}$پj$1 - \omega^2 L C \lt 0$ ‚ج‚ئ‚«
$1 - \omega^2 L C \lt 0$ ‚ج‚ئ‚«‚ح⑤ژ®‚ج $j$ ‚ة‚©‚©‚é’l‚ھ•‰‚ئ‚¢‚¤‚±‚ئ‚ة‚ب‚é‚ج‚إپAچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚جƒxƒNƒgƒ‹‚حپAژں‚ج‚و‚¤‚ة‰؛Œü‚«‚ة‚ب‚è‚ـ‚·پB
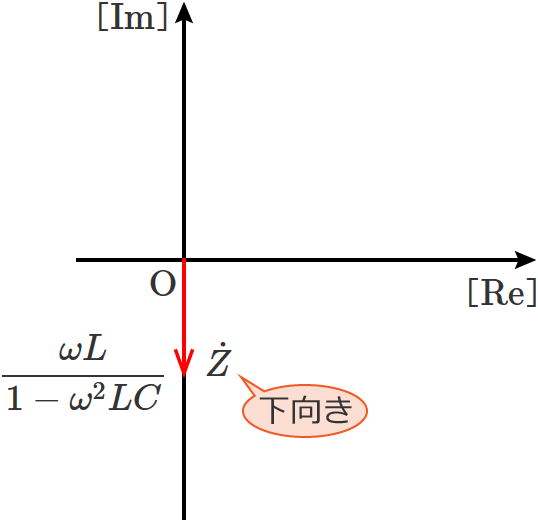
پi$\mathrm{C}$پj$1 - \omega^2 L C = 0$ ‚ج‚ئ‚«
$1 - \omega^2 L C = 0$ ‚ج‚ئ‚«‚ح⑤ژ®‚ج $j$ ‚ة‚©‚©‚é’l‚ھ–³Œہ‘ه‚ة‚ب‚é‚ج‚إپAچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX $\dot{Z}$ ‚ح–³Œہ‘ه‚ة‚ب‚ء‚ؤ‚µ‚ـ‚¢‚ـ‚·پBپi‚ ‚é’l‚ًƒ[ƒچ‚إٹ„‚é‚ئ–³Œہ‘ه‚ة‚ب‚è‚ـ‚·پBپj
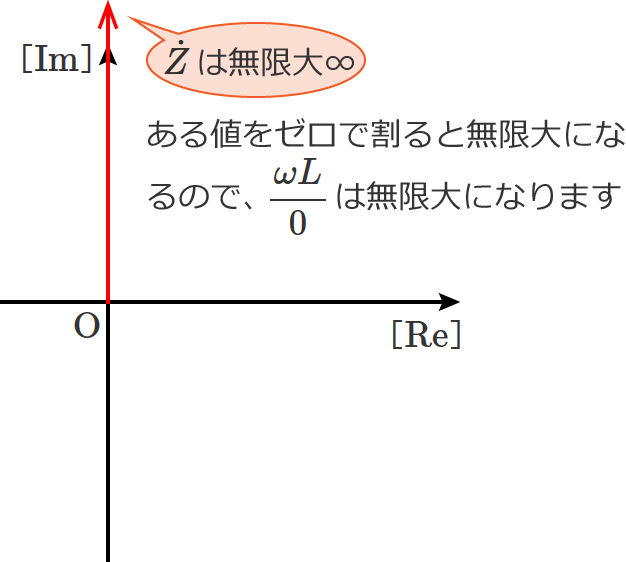
ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ھ–³Œہ‘ه‚ئ‚¢‚¤‚±‚ئ‚حپA‚»‚ج‰ٌکH‚حٹJ•ْڈَ‘ش‚ئ“¯‚¶‚ة‚ب‚è‚ـ‚·پB
‚؟‚ب‚ف‚ةپA$1 - \omega^2 L C = 0$ ‚·‚ب‚ي‚؟پA$\omega = \dfrac{1}{\sqrt{L C}}$ ‚حپA‰ٌکH‚ج‹¤گUڈًŒڈ‚ة‚ب‚è‚ـ‚·پB‹¤گU‚ة‚آ‚¢‚ؤ‚حپA‚±‚؟‚ç‚جRLC•ہ—ٌ‹¤گU‰ٌکH‚جƒyپ[ƒW‚ًژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
ˆبڈم‚ھ‘fژq2Œآ‚ً•ہ—ٌگع‘±‚µ‚½ڈêچ‡‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ة‚ب‚è‚ـ‚·پB
ƒXƒ|ƒ“ƒTپ[ƒٹƒ“ƒN
ƒXƒ|ƒ“ƒTپ[ƒٹƒ“ƒN
‘¼‚ج‰ٌکH‚ة‚آ‚¢‚ؤ‚àƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جŒvژZ‚ً‚µ‚ؤ‚¢‚ـ‚·‚ج‚إپA‚»‚ꂼ‚êژں‚جƒyپ[ƒW‚ًژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
RپALپAC‚جƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ح‚±‚؟‚ç
پثپ@Œً—¬‰ٌکH‚جƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جŒvژZپi‘fژq‚ھ1Œآ‚جڈêچ‡پj
RL’¼—ٌ‰ٌکHپARC’¼—ٌ‰ٌکHپALC’¼—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ح‚±‚؟‚ç
پثپ@Œً—¬‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جŒvژZپi‘fژq‚ھ2Œآ’¼—ٌگع‘±‚جڈêچ‡پj
RLC’¼—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ح‚±‚؟‚ç
پثپ@Œً—¬‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جŒvژZپiRLC’¼—ٌ‰ٌکHپj
RLC•ہ—ٌ‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ح‚±‚؟‚ç
پثپ@Œً—¬‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جŒvژZپiRLC•ہ—ٌ‰ٌکHپj
RL•ہ—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}‚ة‚آ‚¢‚ؤ‚ح‚±‚؟‚ç
پثپ@Œً—¬‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}پiRL•ہ—ٌ‰ٌکHپj
RC•ہ—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}‚ة‚آ‚¢‚ؤ‚ح‚±‚؟‚ç
پثپ@Œً—¬‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}پiRC•ہ—ٌ‰ٌکHپj
LC•ہ—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}‚ة‚آ‚¢‚ؤ‚ح‚±‚؟‚ç
پثپ@Œً—¬‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}پiLC•ہ—ٌ‰ٌکHپj
‚ًژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
’ïچR‚جچ‡گ¬’ïچR‚ة‚آ‚¢‚ؤ‚حپA‚±‚؟‚ç‚جچ‡گ¬’ïچR‚ج‹پ‚ك•ûپiŒvژZ•û–@پj‚جƒyپ[ƒW‚ًژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
ƒXƒ|ƒ“ƒTپ[ƒٹƒ“ƒN
Œً—¬‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جŒvژZپi‘fژq‚ھ2Œآ•ہ—ٌگع‘±‚جڈêچ‡پjپ@ٹضکAƒyپ[ƒW
- ƒCƒ“ƒsپ[ƒ_ƒ“ƒX
- ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پBŒً—¬‰ٌکH‚إ‚ج“dˆ³‚ئ“d—¬‚ج”ن‚ًƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ئ‚¢‚¢پAƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‘ه‚«‚³‚حپAŒً—¬“d—¬‚ج—¬‚ê‚ة‚‚³‚ً•\‚ي‚µ‚ـ‚·پBƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‹پ‚ك•û‚âپAƒCƒ“ƒsپ[ƒ_ƒ“ƒXژOٹpŒ`پAƒCƒ“ƒsپ[ƒ_ƒ“ƒXٹp‚ب‚ا‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- •،‘fƒCƒ“ƒsپ[ƒ_ƒ“ƒX
- •،‘fƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB•،‘fگ”‚إ•\‚ي‚³‚ꂽƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ً•،‘fƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ئ‚¢‚¢پA•،‘fƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جژہ•”‚ح’ïچRپA‹••”‚حƒٹƒAƒNƒ^ƒ“ƒX‚ً•\‚ي‚µ‚ـ‚·پB‚¢‚ë‚¢‚ë‚بŒً—¬‰ٌکH‚ج•،‘fƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‹پ‚ك•û‚ب‚ا‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- ƒAƒhƒ~ƒ^ƒ“ƒX
- ƒAƒhƒ~ƒ^ƒ“ƒX‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پBƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ج‹tگ”‚ًƒAƒhƒ~ƒ^ƒ“ƒX‚ئ‚¢‚¢پAƒAƒhƒ~ƒ^ƒ“ƒX‚ج‘ه‚«‚³‚حپAŒً—¬“d—¬‚ج—¬‚ê‚â‚·‚³‚ً•\‚ي‚µ‚ـ‚·پBƒAƒhƒ~ƒ^ƒ“ƒX‚ج‹پ‚ك•û‚âپAƒAƒhƒ~ƒ^ƒ“ƒXژOٹpŒ`پAƒAƒhƒ~ƒ^ƒ“ƒXٹp‚ب‚ا‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- •،‘fƒAƒhƒ~ƒ^ƒ“ƒX
- •،‘fƒAƒhƒ~ƒ^ƒ“ƒX‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB•،‘fگ”‚إ•\‚ي‚³‚ꂽƒAƒhƒ~ƒ^ƒ“ƒX‚ً•،‘fƒAƒhƒ~ƒ^ƒ“ƒX‚ئ‚¢‚¢پA•،‘fƒAƒhƒ~ƒ^ƒ“ƒX‚جژہ•”‚حƒRƒ“ƒ_ƒNƒ^ƒ“ƒXپA‹••”‚حƒTƒZƒvƒ^ƒ“ƒX‚ً•\‚ي‚µ‚ـ‚·پB‚¢‚ë‚¢‚ë‚بŒً—¬‰ٌکH‚ج•،‘fƒAƒhƒ~ƒ^ƒ“ƒX‚ج‹پ‚ك•û‚ب‚ا‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- Œً—¬‰ٌکH‚جƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جŒvژZپi‘fژq‚ھ1Œآ‚جڈêچ‡پj
- ‘fژqپi’ïچRRپAƒRƒCƒ‹LپAƒRƒ“ƒfƒ“ƒTCپj‚ھ1Œآ‚جڈêچ‡‚جƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB‘fژqپiRپALپACپj‚ھ1Œآ‚ب‚ج‚إپAŒvژZ‚ئ‚¢‚¤‚ظ‚ا‚جŒvژZ‚à‚ب‚‹پ‚ك‚ç‚ê‚ـ‚·‚ھپA‚ئ‚è‚ ‚¦‚¸ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جŒvژZ‚جٹî‘b‚ب‚ج‚إپEپEپEپB
- Œً—¬‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جŒvژZپi‘fژq‚ھ2Œآ’¼—ٌگع‘±‚جڈêچ‡پj
- ‘fژqپi’ïچRRپAƒRƒCƒ‹LپAƒRƒ“ƒfƒ“ƒTCپj‚ھ2Œآ’¼—ٌگع‘±‚³‚ꂽڈêچ‡پiRL’¼—ٌ‰ٌکHپARC’¼—ٌ‰ٌکH,LC’¼—ٌ‰ٌکHپj‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ًŒvژZ‚µ‚ؤ‚¢‚ـ‚·پBLC’¼—ٌ‰ٌکH‚جڈêچ‡‚ة‚حپAƒRƒCƒ‹L‚ئƒRƒ“ƒfƒ“ƒTC‚جƒٹƒAƒNƒ^ƒ“ƒX‚ج‘ه‚«‚³‚ة‚و‚ء‚ؤچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جƒxƒNƒgƒ‹‚جŒü‚«‚ھ•د‚ي‚é‚ج‚إ‹C‚ً•t‚¯‚ـ‚µ‚ه‚¤پB
- Œً—¬‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جŒvژZپiRLC’¼—ٌ‰ٌکHپj
- ‘fژqپi’ïچRRپAƒRƒCƒ‹LپAƒRƒ“ƒfƒ“ƒTCپj‚ھ3Œآ’¼—ٌگع‘±‚³‚ꂽڈêچ‡پiRLC’¼—ٌ‰ٌکHپj‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ًŒvژZ‚µ‚ؤ‚¢‚ـ‚·پBRLC’¼—ٌ‰ٌکH‚جڈêچ‡پAƒRƒCƒ‹L‚ئƒRƒ“ƒfƒ“ƒTC‚جƒٹƒAƒNƒ^ƒ“ƒX‚ج‘ه‚«‚³‚ھ“¯‚¶‚ئ‚«‚ة‚حچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ح’ïچRR‚¾‚¯‚ة‚ب‚è‚ـ‚·پB‚±‚ê‚ح‚·‚²‚‘هژ–‚ب‚±‚ئ‚ب‚ج‚إ‚¨‚ع‚¦‚ؤ‚¨‚«‚ـ‚µ‚ه‚¤پI
- Œً—¬‰ٌکH‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚جŒvژZپiRLC•ہ—ٌ‰ٌکHپj
- ‘fژqپi’ïچRRپAƒRƒCƒ‹LپAƒRƒ“ƒfƒ“ƒTCپj‚ھ3Œآ•ہ—ٌگع‘±‚³‚ꂽڈêچ‡پiRLC•ہ—ٌ‰ٌکHپj‚جچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ًŒvژZ‚µ‚ؤ‚¢‚ـ‚·پBRLC•ہ—ٌ‰ٌکH‚جڈêچ‡پAژü”gگ”‚ھ”½‹¤گUژü”gگ”‚ج‚ئ‚«ƒRƒCƒ‹L‚ئƒRƒ“ƒfƒ“ƒTC‚ج•ہ—ٌ‰ٌکH•”•ھ‚ھ‰ً•ْڈَ‘ش‚ئ“¯‚¶‚ة‚ب‚邽‚كپAچ‡گ¬ƒCƒ“ƒsپ[ƒ_ƒ“ƒX‚ح’ïچRR‚¾‚¯‚ة‚ب‚è‚ـ‚·پB
- RLC’¼—ٌ‹¤گU‰ٌکH
- RLC’¼—ٌ‹¤گU‰ٌکH‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پBRLC’¼—ٌ‹¤گU‰ٌکH‚حƒtƒBƒ‹ƒ^‰ٌکH‚ب‚ا“d‹C‚إ•چL‚‰—p‚³‚ê‚ؤ‚¢‚é‰ٌکH‚إ‚·‚ج‚إپA‹¤گUژü”gگ”‚ب‚اٹî–{“I‚ب‚±‚ئ‚¾‚¯‚إ‚à‚¨‚ع‚¦‚ؤ‚¨‚‚و‚¤‚ة‚µ‚ـ‚µ‚ه‚¤پB
- RLC•ہ—ٌ‹¤گU‰ٌکH
- RLC•ہ—ٌ‹¤گU‰ٌکH‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پBRLC•ہ—ٌ‹¤گU‰ٌکH‚ب‚ا‚ج‹¤گU‰ٌکH‚ح“d‹C‚إ•چL‚‰—p‚³‚ê‚ؤ‚¢‚é‰ٌکH‚إ‚·‚ج‚إپA‹¤گUژü”gگ”‚ب‚اٹî–{“I‚ب‚±‚ئ‚¾‚¯‚إ‚à‚¨‚ع‚¦‚ؤ‚¨‚‚و‚¤‚ة‚µ‚ـ‚µ‚ه‚¤پB
- گ³Œ·”gŒً—¬”gŒ`‚جژہŒّ’l‚ح‚ب‚؛چإ‘ه’lپ€پم2‚©پH
- گ³Œ·”gŒً—¬”gŒ`‚جژہŒّ’l‚ً‹پ‚ك‚é‚ئ‚«‚حچإ‘ه’l‚ًپم2‚إٹ„‚ê‚خ‚¢‚¢‚إ‚·‚ھپA‚إ‚حپA‚ب‚؛پم2‚إٹ„‚ê‚خژہŒّ’l‚ة‚ب‚é‚ج‚إ‚µ‚ه‚¤‚©پHگ³Œ·”gŒً—¬”gŒ`‚جژہŒّ’l‚ھچإ‘ه’lپ€پم2‚ة‚ب‚邱‚ئ‚ًŒvژZ‚إ“±‚¢‚ؤ‚ف‚ـ‚µ‚½‚ج‚إژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB‘S”gگ®—¬”gŒ`پA”¼”gگ®—¬”gŒ`پA•ûŒ`”gپA‚ج‚±‚¬‚è”g‚ة‚آ‚¢‚ؤ‚àژہŒّ’l‚ًŒvژZ‚µ‚ؤ‚ف‚ـ‚µ‚½پB
- ‚ب‚؛ƒRƒCƒ‹‚ة—¬‚ê‚é“d—¬‚جˆت‘ٹ‚ح“dˆ³‚و‚è90پ‹’x‚ê‚é‚ج‚©پH
- ƒRƒCƒ‹‚ة—¬‚ê‚é“d—¬‚جˆت‘ٹ‚ح“dˆ³‚و‚è‚à90پ‹’x‚ê‚ـ‚·‚ھپAƒRƒCƒ‹‚جڈêچ‡پA‚ب‚؛“d—¬‚ھ“dˆ³‚و‚è‚à90پ‹’x‚êˆت‘ٹ‚ة‚ب‚é‚ج‚©‚ًŒvژZ‚إ“±‚¢‚ؤ‚¢‚ـ‚·پB
- ‚ب‚؛ƒRƒ“ƒfƒ“ƒT‚ة—¬‚ê‚é“d—¬‚جˆت‘ٹ‚ح“dˆ³‚و‚è90پ‹گi‚ق‚ج‚©پH
- ƒRƒ“ƒfƒ“ƒT‚ة—¬‚ê‚é“d—¬‚جˆت‘ٹ‚ح“dˆ³‚و‚è‚à90پ‹گi‚ف‚ـ‚·‚ھپAƒRƒ“ƒfƒ“ƒT‚جڈêچ‡پA‚ب‚؛“d—¬‚ھ“dˆ³‚و‚è‚à90پ‹گi‚فˆت‘ٹ‚ة‚ب‚é‚ج‚©‚ًŒvژZ‚إ“±‚¢‚ؤ‚¢‚ـ‚·پB
- Œً—¬‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}پi’ïچR‚¾‚¯‚ج‰ٌکHپj
- گ³Œ·”gŒً—¬“dŒ¹‚ة’ïچR‚¾‚¯گع‘±‚³‚ê‚ؤ‚¢‚éŒً—¬‰ٌکH‚ج‰ٌکH‚ة—¬‚ê‚é“d—¬‚ئپA’ïچR‚ة‚©‚©‚é“dˆ³‚جŒvژZ•û–@‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB“dˆ³‚ئ“d—¬‚جƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إپAŒً—¬‰ٌکH‚جŒvژZ‚âƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚جژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- Œً—¬‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}پiƒRƒCƒ‹‚¾‚¯‚ج‰ٌکHپj
- گ³Œ·”gŒً—¬“dŒ¹‚ةƒRƒCƒ‹‚¾‚¯گع‘±‚³‚ê‚ؤ‚¢‚éŒً—¬‰ٌکH‚ج‰ٌکH‚ة—¬‚ê‚é“d—¬‚ئپAƒRƒCƒ‹‚ة‚©‚©‚é“dˆ³‚جŒvژZ•û–@‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB“dˆ³‚ئ“d—¬‚جƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إپAŒً—¬‰ٌکH‚جŒvژZ‚âƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚جژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- Œً—¬‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}پiƒRƒ“ƒfƒ“ƒT‚¾‚¯‚ج‰ٌکHپj
- گ³Œ·”gŒً—¬“dŒ¹‚ةƒRƒ“ƒfƒ“ƒT‚¾‚¯گع‘±‚³‚ê‚ؤ‚¢‚éŒً—¬‰ٌکH‚ج‰ٌکH‚ة—¬‚ê‚é“d—¬‚ئپAƒRƒ“ƒfƒ“ƒT‚ة‚©‚©‚é“dˆ³‚جŒvژZ•û–@‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB“dˆ³‚ئ“d—¬‚جƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إپAŒً—¬‰ٌکH‚جŒvژZ‚âƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚جژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- Œً—¬‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}پiRL’¼—ٌ‰ٌکHپj
- RL’¼—ٌ‰ٌکHپiŒً—¬‰ٌکHپj‚جٹe‘fژq‚ة‚©‚©‚é“dˆ³پA’¼—ٌگع‘±‘S‘ج‚ة‚©‚©‚é“dˆ³پAˆت‘ٹچ·‚جŒvژZ•û–@‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پBRL’¼—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إپARL’¼—ٌ‰ٌکH‚جŒvژZ‚âƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚جژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- Œً—¬‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}پiRC’¼—ٌ‰ٌکHپj
- RC’¼—ٌ‰ٌکHپiŒً—¬‰ٌکHپj‚جٹe‘fژq‚ة‚©‚©‚é“dˆ³پA’¼—ٌگع‘±‘S‘ج‚ة‚©‚©‚é“dˆ³پAˆت‘ٹچ·‚جŒvژZ•û–@‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پBRC’¼—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إپARC’¼—ٌ‰ٌکH‚جŒvژZ‚âƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚جژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- Œً—¬‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}پiRLC’¼—ٌ‰ٌکHپj
- RLC’¼—ٌ‰ٌکHپiŒً—¬‰ٌکHپj‚جٹe‘fژq‚ة‚©‚©‚é“dˆ³پA’¼—ٌگع‘±‘S‘ج‚ة‚©‚©‚é“dˆ³پAˆت‘ٹچ·‚جŒvژZ•û–@‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پBRLC’¼—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إپARLC’¼—ٌ‰ٌکH‚جŒvژZ‚âƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚جژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- Œً—¬‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}پiRL•ہ—ٌ‰ٌکHپj
- RL•ہ—ٌ‰ٌکHپiŒً—¬‰ٌکHپj‚جٹe‘fژq‚ة—¬‚ê‚é“d—¬پA‰ٌکH‘S‘ج‚ة—¬‚ê‚é“d—¬پAˆت‘ٹچ·‚جŒvژZ•û–@‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پBRL•ہ—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إپARL•ہ—ٌ‰ٌکH‚جŒvژZ‚âƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚جژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- Œً—¬‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}پiRC•ہ—ٌ‰ٌکHپj
- RC•ہ—ٌ‰ٌکHپiŒً—¬‰ٌکHپj‚جٹe‘fژq‚ة—¬‚ê‚é“d—¬پA‰ٌکH‘S‘ج‚ة—¬‚ê‚é“d—¬پAˆت‘ٹچ·‚جŒvژZ•û–@‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پBRC•ہ—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إپARC•ہ—ٌ‰ٌکH‚جŒvژZ‚âƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚جژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- Œً—¬‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}پiLC•ہ—ٌ‰ٌکHپj
- LC•ہ—ٌ‰ٌکHپiŒً—¬‰ٌکHپj‚جٹe‘fژq‚ة—¬‚ê‚é“d—¬‚ئپA‰ٌکH‘S‘ج‚ة—¬‚ê‚é“d—¬‚جŒvژZ•û–@‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پBLC•ہ—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إپALC•ہ—ٌ‰ٌکH‚جŒvژZ‚âƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚جژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- Œً—¬‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ‚ئƒxƒNƒgƒ‹گ}پiRLC•ہ—ٌ‰ٌکHپj
- RLC•ہ—ٌ‰ٌکHپiŒً—¬‰ٌکHپj‚جٹe‘fژq‚ة—¬‚ê‚é“d—¬پA‰ٌکH‘S‘ج‚ة—¬‚ê‚é“d—¬پAˆت‘ٹچ·‚جŒvژZ•û–@‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پBRLC•ہ—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إپARLC•ہ—ٌ‰ٌکH‚جŒvژZ‚âƒxƒNƒgƒ‹گ}‚ج•`‚«•û‚جژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- RL’¼—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZپi“dŒ¹‚ج“dˆ³‚ًٹîڈ€‚ة‚µ‚½ڈêچ‡پj
- RL’¼—ٌ‰ٌکH‚ج‰ٌکH‚ة—¬‚ê‚é“d—¬‚ئٹe‘fژq‚ة‚©‚©‚é“dˆ³‚ً“dŒ¹‚ج“dˆ³‚ًٹîڈ€‚ة‚µ‚ؤŒvژZ‚µ‚ؤ‚¢‚ـ‚·‚ج‚إپARL’¼—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ•û–@‚جژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- RC’¼—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZپi“dŒ¹‚ج“dˆ³‚ًٹîڈ€‚ة‚µ‚½ڈêچ‡پj
- RC’¼—ٌ‰ٌکH‚ج‰ٌکH‚ة—¬‚ê‚é“d—¬‚ئٹe‘fژq‚ة‚©‚©‚é“dˆ³‚ً“dŒ¹‚ج“dˆ³‚ًٹîڈ€‚ة‚µ‚ؤŒvژZ‚µ‚ؤ‚¢‚ـ‚·‚ج‚إپARC’¼—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ•û–@‚جژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- RLC’¼—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZپi“dŒ¹‚ج“dˆ³‚ًٹîڈ€‚ة‚µ‚½ڈêچ‡پj
- RLC’¼—ٌ‰ٌکH‚ج‰ٌکH‚ة—¬‚ê‚é“d—¬‚ئٹe‘fژq‚ة‚©‚©‚é“dˆ³‚ً“dŒ¹‚ج“dˆ³‚ًٹîڈ€‚ة‚µ‚ؤŒvژZ‚µ‚ؤ‚¢‚ـ‚·‚ج‚إپARLC’¼—ٌ‰ٌکH‚ج“dˆ³‚ئ“d—¬‚جŒvژZ•û–@‚جژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- Œً—¬‰ٌکH‚ج“d—ح‚جŒvژZپi’ïچR‚¾‚¯‚ج‰ٌکHپj
- •‰‰×‚ھ’ïچR‚¾‚¯‚جڈêچ‡‚جŒً—¬‰ٌکH‚ج“d—حپiڈuژ“d—حپA•½‹د“d—حپj‚جŒvژZ•û–@پi‹پ‚ك•ûپjپA“d—ح‚ج”gŒ`‚ب‚ا‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB
- Œً—¬‰ٌکH‚ج“d—ح‚جŒvژZپiƒRƒCƒ‹‚¾‚¯‚ج‰ٌکHپj
- •‰‰×‚ھƒRƒCƒ‹‚¾‚¯‚جڈêچ‡‚جŒً—¬‰ٌکH‚ج“d—حپiڈuژ“d—حپA•½‹د“d—حپj‚جŒvژZ•û–@پi‹پ‚ك•ûپjپA“d—ح‚ج”gŒ`‚ب‚ا‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB
- Œً—¬‰ٌکH‚ج“d—ح‚جŒvژZپiƒRƒ“ƒfƒ“ƒT‚¾‚¯‚ج‰ٌکHپj
- •‰‰×‚ھƒRƒ“ƒfƒ“ƒT‚¾‚¯‚جڈêچ‡‚جŒً—¬‰ٌکH‚ج“d—حپiڈuژ“d—حپA•½‹د“d—حپj‚جŒvژZ•û–@پi‹پ‚ك•ûپjپA“d—ح‚ج”gŒ`‚ب‚ا‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB
- Œً—¬‰ٌکH‚ج“d—ح‚جŒvژZپiRL’¼—ٌ‰ٌکHپj
- RL’¼—ٌ‰ٌکH‚ج“d—حپiڈuژ“d—حپA•½‹د“d—حپj‚جŒvژZ•û–@پi‹پ‚ك•ûپjپA“d—ح‚ج”gŒ`‚ب‚ا‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB
- Œً—¬‰ٌکH‚ج“d—ح‚جŒvژZپiRC’¼—ٌ‰ٌکHپj
- RC’¼—ٌ‰ٌکH‚ج“d—حپiڈuژ“d—حپA•½‹د“d—حپj‚جŒvژZ•û–@پi‹پ‚ك•ûپjپA“d—ح‚ج”gŒ`‚ب‚ا‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB
- —LŒّپE–³ŒّپE”ç‘ٹ“d—ح
- Œً—¬‰ٌکH‚ة‚حپu—LŒّ“d—حپvپu–³Œّ“d—حپvپu”ç‘ٹ“d—حپv‚ج3ژي—ق‚ج“d—ح‚ھ‚ ‚è‚ـ‚·پB‚»‚ꂼ‚ê‚ج“d—ح‚ج‹پ‚ك•û‚ئپA3‚آ‚ج“d—ح‚جٹضŒW‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB
- —ح—¦‚ئ‚حپHپi—ح—¦‚ئ“d—ح‚جٹضŒWپj
- Œً—¬‰ٌکH‚ج•×‹‚ً‚µ‚ؤ‚¢‚é‚ئپu—ح—¦پv‚ھ‚إ‚ؤ‚«‚ـ‚·‚ھپA—ح—¦‚ء‚ؤ‰½‚إ‚µ‚ه‚¤‚©پH—ح—¦‚جژ®‚ج•\‚µ•û‚ة‚حگFپX‚ ‚è‚ـ‚·‚ھپA‚±‚±‚إ‚حپA—ح—¦‚ئ”ç‘ٹ“d—حپA—LŒّ“d—حپA–³Œّ“d—ح‚جٹضŒW‚ئ‚»‚جٹضŒWژ®‚ب‚ا‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ـ‚·پB
- —ح—¦‚ئ‚حپHپi—ح—¦‚ئˆت‘ٹ‚جٹضŒWپj
- Œً—¬‰ٌکH‚ج•×‹‚ً‚µ‚ؤ‚¢‚é‚ئپu—ح—¦(cosƒ¦)پv‚ھ‚إ‚ؤ‚«‚ـ‚·‚ھپA—ح—¦‚ء‚ؤ‰½‚إ‚µ‚ه‚¤‚©پH—ح—¦‚جژ®‚ج•\‚µ•û‚ة‚حگFپX‚ ‚è‚ـ‚·‚ھپA‚±‚±‚إ‚حپAˆت‘ٹ‚ئ—ح—¦‚جٹضŒW‚ة‚آ‚¢‚ؤ’ïچRپAƒRƒCƒ‹پAƒRƒ“ƒfƒ“ƒT‚ج‰ٌکH‚ً—ل‚ة‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB
- ”gŒ`‚جژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚ج‹پ‚ك•û
- ”gŒ`‚حگFپX‚ ‚è‚ـ‚·‚ھپA‚»‚ج”gŒ`‚ج“ءگ«‚ً•\‚ي‚·’l‚ئ‚µ‚ؤژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚ب‚ا‚ھ‚ ‚è‚ـ‚·پB‚±‚±‚إ‚حپA”gŒ`‚جژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚ج’è‹`ژ®پA‹پ‚ك•û‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB
- گ³Œ·”g”gŒ`‚جژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚جŒvژZ•û–@
- ”gŒ`‚حگFپX‚ ‚è‚ـ‚·‚ھپA‚»‚ج”gŒ`‚ج“ءگ«‚ً•\‚ي‚·’l‚ئ‚µ‚ؤژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚ب‚ا‚ھ‚ ‚è‚ـ‚·پB‚±‚±‚إ‚حپAگ³Œ·”g”gŒ`‚جژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚جŒvژZ•û–@پA‹پ‚ك•û‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB
- ‘S”gگ®—¬”gŒ`‚جژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚جŒvژZ•û–@
- ”gŒ`‚حگFپX‚ ‚è‚ـ‚·‚ھپA‚»‚ج”gŒ`‚ج“ءگ«‚ً•\‚ي‚·’l‚ئ‚µ‚ؤژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚ب‚ا‚ھ‚ ‚è‚ـ‚·پB‚±‚±‚إ‚حپA‘S”gگ®—¬”gŒ`‚جژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚جŒvژZ•û–@پA‹پ‚ك•û‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB
- ”¼”gگ®—¬”gŒ`‚جژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚جŒvژZ•û–@
- ”¼”gگ®—¬”gŒ`‚جژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚جŒvژZ•û–@پA‹پ‚ك•û‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB”gŒ`‚ج“ءگ«‚ً•\‚ي‚·’l‚ئ‚µ‚ؤژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚ب‚ا‚ھ‚ ‚è‚ـ‚·‚ھپA‚±‚ê‚ç‚ح‘هژ–‚ب’l‚إ‚·‚ج‚إپA‹پ‚ك•ûپAŒvژZ•û–@‚ً‚¨‚ع‚¦‚ؤ‚¨‚«‚ـ‚µ‚ه‚¤پB
- •ûŒ`”g”gŒ`‚جژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚جŒvژZ•û–@
- •ûŒ`”g”gŒ`‚جژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚جŒvژZ•û–@پA‹پ‚ك•û‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB•ûŒ`”g”gŒ`‚جڈêچ‡پAژہŒّ’l‚ئ•½‹د’l‚ئچإ‘ه’l‚ھ“¯‚¶’lپA”gŒ`—¦‚ئ”gچ‚—¦‚ھ“¯‚¶’l‚ة‚ب‚è‚ـ‚·پB‚؟‚ب‚ف‚ةپA•ûŒ`”g‚ئ‹éŒ`”g‚ح“¯‚¶‚إ‚·پB
- ‚ج‚±‚¬‚è”g”gŒ`‚جژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚جŒvژZ•û–@
- ‚ج‚±‚¬‚è”g”gŒ`‚جژہŒّ’lپA•½‹د’lپAچإ‘ه’lپA”gŒ`—¦پA”gچ‚—¦‚جŒvژZ•û–@پA‹پ‚ك•û‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB‚ج‚±‚¬‚è”g”gŒ`‚جژہŒّ’l‚ئ•½‹د’l‚ً‹پ‚ك‚邽‚ك‚ة‚حپA‚ج‚±‚¬‚è”g”gŒ`‚جژ®‚©‚çچl‚¦‚ب‚¢‚ئ‚¢‚¯‚ب‚¢‚ج‚إپA‘¼‚ج”gŒ`‚و‚è‚àŒvژZ‚ھ‚؟‚ه‚ء‚ئ‘ه•د‚إ‚·پB
- ژO‘ٹ“d—ح‚جŒِژ®‚ح‚ب‚؛پم3”{‚ب‚ج‚©پHپiژO‘ٹ“d—ح‚جŒِژ®‚ج“±ڈoپj
- ژO‘ٹ“d—ح‚جŒِژ®‚حPپپپم3VIcosƒس‚إ•\‚ي‚³‚ê‚ـ‚·‚ھپA‚ب‚؛پم3”{‚ة‚ب‚é‚ج‚©پHƒXƒ^پ[Œ‹گü‚جڈêچ‡‚ئƒfƒ‹ƒ^Œ‹گü‚جڈêچ‡‚»‚ꂼ‚ê‚ة‚آ‚¢‚ؤپAژO‘ٹ“d—ح‚جŒِژ®‚ً“±ڈo‚µ‚ؤ‚ف‚ـ‚µ‚½پB‚±‚جژO‘ٹ“d—ح‚جŒِژ®‚ح“dŒ±ژOژي‚جپu—ک_پvپu“d—حپv‰ب–ع‚ج–â‘è‚ً‰ً‚‚ئ‚«‚ة“xپXژg‚ي‚ê‚éٹî–{“I‚بŒِژ®‚إ‚·‚ج‚إ‚¨‚ع‚¦‚ؤ‚¨‚‚و‚¤‚ة‚µ‚ـ‚µ‚ه‚¤پB
- ƒXƒ^پ[Œ‹گüپiYŒ‹گüپj‚جگüٹش“dˆ³‚ح‚ب‚؛‘ٹ“dˆ³‚جپم3”{‚ة‚ب‚é‚ج‚©پH
- ƒXƒ^پ[Œ‹گüپiYŒ‹گüپj‚³‚ê‚ؤ‚¢‚éژO‘ٹŒً—¬‰ٌکH‚جگüٹش“dˆ³‚ح‘ٹ“dˆ³‚جپم3”{‚ة‚ب‚è‚ـ‚·‚ھپA‚ب‚؛پم3”{‚ة‚ب‚é‚ج‚©پHƒXƒ^پ[Œ‹گü‚ج‚ئ‚«‚جگüٹش“dˆ³‚ئ‘ٹ“dˆ³‚جƒxƒNƒgƒ‹گ}‚ً‹پ‚كپA‹پ‚ك‚½ƒxƒNƒgƒ‹گ}‚©‚çپم3”{‚ة‚ب‚é——R‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پB
- ƒfƒ‹ƒ^ƒXƒ^پ[•دٹ·پiƒ¢پ¨Y•دٹ·پj
- ƒfƒ‹ƒ^ƒXƒ^پ[•دٹ·پiƒ¢پ¨Y•دٹ·پj‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پBƒfƒ‹ƒ^Œ‹گüپiƒ¢Œ‹گüپj‚ً“™‰؟‚بƒXƒ^پ[Œ‹گüپiYŒ‹گüپj‚ة•دٹ·‚·‚é‚ج‚ًƒfƒ‹ƒ^ƒXƒ^پ[•دٹ·پiƒ¢پ¨Y•دٹ·پj‚ئ‚¢‚¢‚ـ‚·پBƒfƒ‹ƒ^ƒXƒ^پ[•دٹ·‚جژ®‚ج“±ڈo•û–@‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- ƒXƒ^پ[ƒfƒ‹ƒ^•دٹ·پiYپ¨ƒ¢•دٹ·پj
- ƒXƒ^پ[ƒfƒ‹ƒ^•دٹ·پiYپ¨ƒ¢•دٹ·پj‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پBƒXƒ^پ[Œ‹گüپiYŒ‹گüپj‚ً“™‰؟‚بƒfƒ‹ƒ^Œ‹گüپiƒ¢Œ‹گüپj‚ة•دٹ·‚·‚é‚ج‚ًƒXƒ^پ[ƒfƒ‹ƒ^•دٹ·پiYپ¨ƒ¢•دٹ·پj‚ئ‚¢‚¢‚ـ‚·پBƒXƒ^پ[ƒfƒ‹ƒ^•دٹ·‚جژ®‚ج“±ڈo•û–@‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB
- Œً—¬‰ٌکH‚جƒeƒuƒiƒ“‚ج’è—
- Œً—¬‰ٌکH‚جƒeƒuƒiƒ“‚ج’è—پi–P-ƒeƒuƒiƒ“‚ج’è—پj‚ة‚آ‚¢‚ؤ‰ًگà‚µ‚ؤ‚¢‚ـ‚·پBƒeƒuƒiƒ“‚ج’è—‚ًژg‚ء‚½Œً—¬‰ٌکH‚جŒvژZ•û–@‚âپAŒً—¬‰ٌکH‚جƒeƒuƒiƒ“‚ج’è—‚جڈط–¾‚ة‚آ‚¢‚ؤ‚à‰ًگà‚µ‚ؤ‚¢‚ـ‚·‚ج‚إژQچl‚ة‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB


