スポンサーリンク
電気数学のお勉強 ラプラス変換
※ページ内にPR･広告が含まれる場合があります。
「ラプラス変換」の関連記事のまとめページです。
ラプラス変換は自動制御でよく使われる数学で、主に、微分方程式を解くときなどに使われています。
自動制御以外にも、例えば過渡現象の解析などで微分方程式を解くときにラプラス変換を使うと計算が楽にできたりします。
ですので、ラプラス変換の使い方をおぼえておくと、電気の計算をするときに何かと便利です。
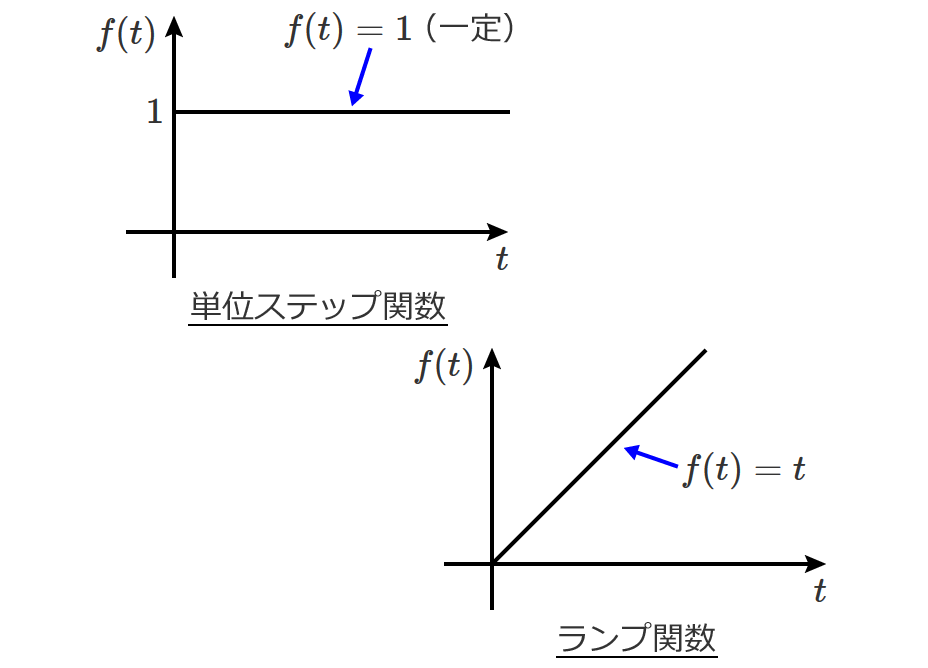
まず初めは、ラプラス変換の定義式とラプラス変換の公式から勉強するといいと思います。
スポンサーリンク
電気数学のお勉強 ラプラス変換 関連記事一覧
ある時間 $t$ の関数 $f(t)$ のラプラス変換 $F(s)$ は、次式で定義されます。$F(s) = \mathcal{L}\left[\, f(t)\, \right] = \displaystyle\int_0^\infty f(t) \, e^{-st} \, dt$したがって、ある時...
ラプラス変換の公式をまとめてみました。ラプラス変換の公式は、あれもこれもと並べると数多くあり、すべての公式をおぼえるのは大変です。なので、このページでは電気数学で「よく使うラプラス変換の公式」、「ほとんど使わないラプラス変換の公式」※に分けてみました。※個人的な公式の使用頻度で分けていますので、人に...
線形性$a$、$b$ を定数とすると、$\mathcal{L} \left[\, a \, f(t) + b \, g(t)\, \right] = a \, F(s) + b \, G(s)$相似法則$a \gt 0$ のとき、$\mathcal{L} \left[\, f(at)\, \righ...
次のように、$f(t) = 1 \quad ( t \geqq 0 )$ で表わされるような関数を単位ステップ関数といいます。$f(t) = \begin{cases} 1 & ( t \geqq 0 ) \\ 0 & ( t \lt 0 ) \end{cases}$この単位ステップ関数 $f(t)...
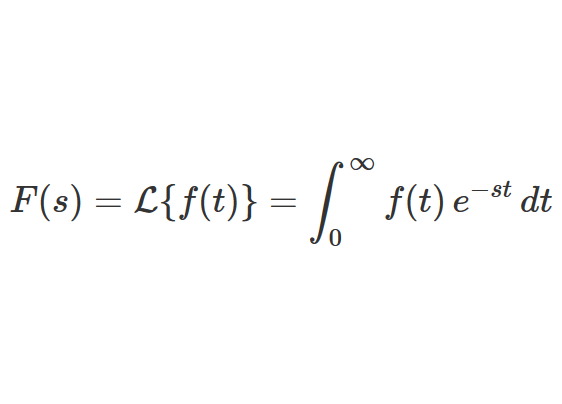
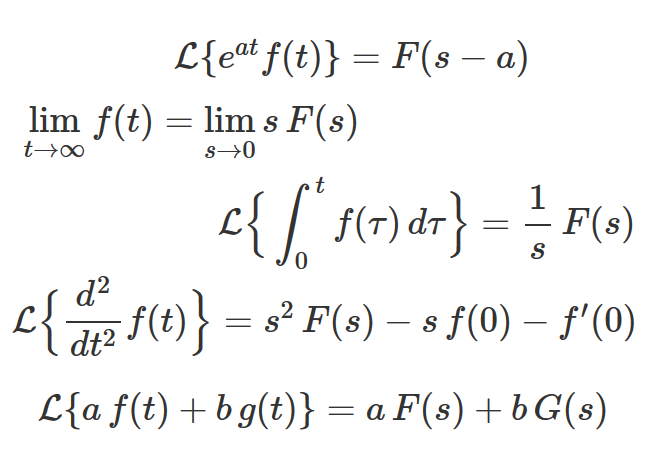
スポンサーリンク
