交流回路のインピーダンスの計算（素子が1個の場合）

※ページ内にPR･広告が含まれる場合があります。

回路の素子（抵抗 $R$ 、コイル $L$ 、コンデンサ $C$ ）が1個の場合のインピーダンスを計算してみます。

素子（ $R$ 、$L$ 、$C$ ）が1個の場合なので計算というほどの計算でもありませんが、インピーダンスを求める計算の基礎の基礎なのでとりあえず…。（ここでつまずいちゃダメですよ。）

ちょっとその前にインピーダンスを表わす記号（表記）について

インピーダンスは、一般的にアルファベットの $Z$ を使って表わします。

インピーダンスはベクトル（大きさと向きがある）なので当然ベクトルで表わされるのですが、電気回路の分野では、ベクトルを表わすときにはアルファベットの上に「・（ドット）」を付けて、

ベクトルです！

ということにしています。（ちなみに、同じ電気の分野でも電気磁気学の分野では、一般的に「・」は使われません。）

なので、電気回路でインピーダンス（ベクトル）を表わすときは、

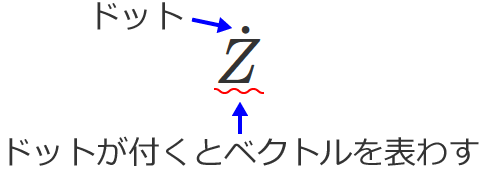
インピーダンス（ベクトル）Zの例

と書かれるのがふつうです。

それからちょっと補足ですが、インピーダンスの大きさのことを言うときも単に「インピーダンス」と言う場合もありますが、この場合は大きさなのでベクトルではなくスカラー（大きさだけで向きがない）になります。
また、複素数の形で表わしたインピーダンスを「複素インピーダンス」、インピーダンスの大きさのことを言うときは「インピーダンス」と言って区別する場合もありますが、ここでは複素インピーダンスを単に「インピーダンス」と書いています。

それでは、ここから本題に入ります。

抵抗Rが1個の場合のインピーダンス

抵抗が1個だけなので、回路は次のようになります。

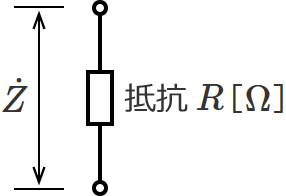
抵抗が1個だけの回路

これは一番簡単なインピーダンスの例ですね。

特に計算する必要もなく、この場合のインピーダンス $\dot{Z}$ は、

$\dot{Z} = R$　［$ \mathrm{\Omega} $］　…①

になります。

抵抗Rが1個の場合のインピーダンスの大きさ

インピーダンス $\dot{Z}$ の大きさは、①式の絶対値を求めればいいです。

って、これも計算する必要はないですね。

$| \dot{Z} | = R$　［$ \mathrm{\Omega} $］

になります。

抵抗Rが1個の場合のインピーダンスのベクトル図

インピーダンスが $\dot{Z} = R$ なので、インピーダンス $\dot{Z}$ のベクトル図は次のようになります。

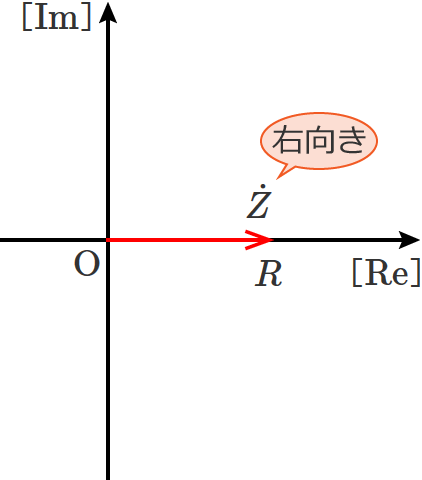
抵抗が1個だけの回路のインピーダンスのベクトル図

抵抗だけの回路の場合、図のように右向きのベクトルになります。

補足

グラフの横軸と縦軸について

グラフの横軸と縦軸に書いてある［$\mathrm{Re}$］と［$\mathrm{Im}$］は、複素平面の実軸と虚軸という意味です。複素平面の実軸には複素数の実部が対応し、虚軸には複素数の虚部が対応します。

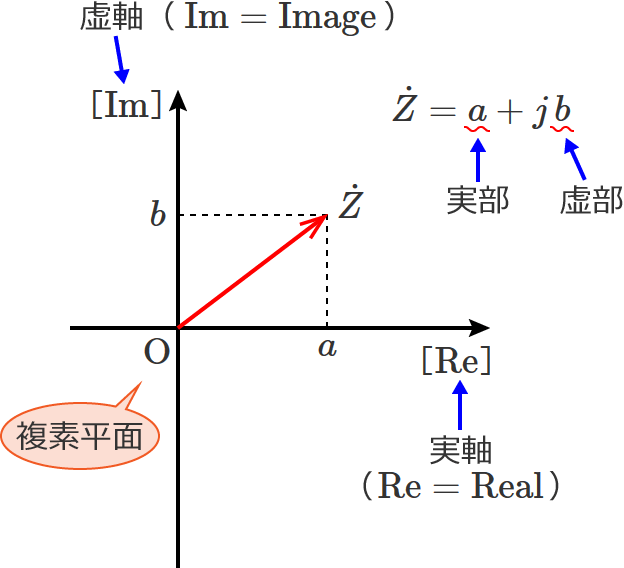
グラフ（複素平面）の縦軸と横軸の説明図（実軸と虚軸）

ちなみに、複素平面は、ガウス平面とか複素数平面ともいいます。

コイルLが1個の場合のインピーダンス

コイルが1個だけなので、回路は次のようになります。

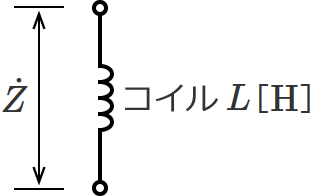
コイルが1個だけの回路

コイルの場合、コイルのリアクタンス $\omega L$ に虚数単位 $j$ をかけて、インピーダンス $\dot{Z}$ は、

$\dot{Z} = j \omega L$　［$ \mathrm{\Omega} $］　…②

になります。（ $\omega$ は角周波数（ $\omega = 2 \pi f$ ）です。）

コイルLが1個の場合のインピーダンスの大きさ

インピーダンス $\dot{Z}$ の大きさは、②式の絶対値を求めればいいので、

$| \dot{Z} | = \sqrt{\left( \omega L \right)^2} = \omega L$

$\therefore | \dot{Z} | = \omega L$　［$ \mathrm{\Omega} $］

になります。

コイルLが1個の場合のインピーダンスのベクトル図

インピーダンスが $\dot{Z} = j \omega L$ なので、インピーダンス $\dot{Z}$ のベクトル図は次のようになります。

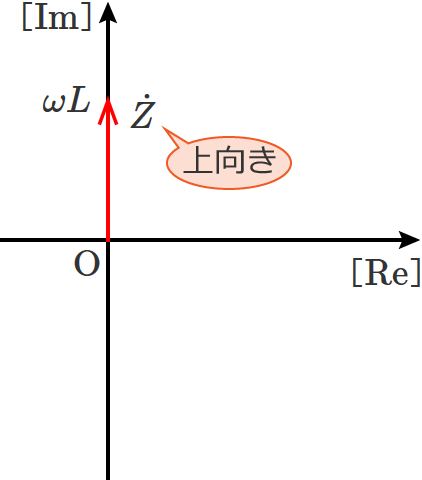
コイルが1個だけの回路のインピーダンスのベクトル図

コイルだけの回路の場合、図のように上向きのベクトルになります。

コンデンサCが1個の場合のインピーダンス

コンデンサが1個だけなので、回路は次のようになります。

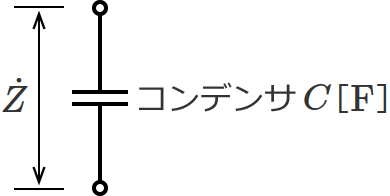
コンデンサが1個だけの回路

コンデンサの場合、コンデンサのリアクタンス $\dfrac{1}{\omega C}$ の分母に $j$ をかけて、インピーダンス $\dot{Z}$ は、

$\dot{Z} = \dfrac{1}{j \omega C}$　［$ \mathrm{\Omega} $］

になります。

このままでもいいですが、分母と分子に $j$ をかけて、

$\dot{Z} = \dfrac{j \times 1}{j \times j \omega C} = \dfrac{j}{-1 \cdot \omega C} = -j \dfrac{1}{\omega C}$

$\therefore \dot{Z} = -j \dfrac{1}{\omega C}$　［$ \mathrm{\Omega} $］　…③

としてもいいです。

あれ？　虚数（ $j$ ）の計算は大丈夫ですよね？

$j \times j = -1$ ですね。

コンデンサCが1個の場合のインピーダンスの大きさ

インピーダンス $\dot{Z}$ の大きさは、③式の絶対値を求めればいいので、

$| \dot{Z} | = \sqrt{\left( -\dfrac{1}{\omega C} \right)^2} = \sqrt{\left( \dfrac{1}{\omega C} \right)^2}$ $= \dfrac{1}{\omega C}$

$\therefore| \dot{Z} | = \dfrac{1}{\omega C}$　［$ \mathrm{\Omega} $］

になります。

コンデンサCが1個の場合のインピーダンスのベクトル図

インピーダンスが $\dot{Z} = -j \dfrac{1}{\omega C}$ なので、インピーダンス $\dot{Z}$ のベクトル図は次のようになります。

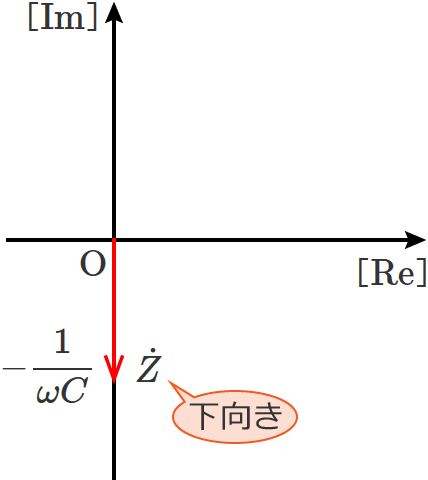
コンデンサが1個だけの回路のインピーダンスのベクトル図

コンデンサの場合は、ベクトルの向きがコイルの場合と逆向き（180°反対向き）になります。

これってものすごく大事なことなのでおぼえておきましょう！

以上が各素子1個だけの場合のインピーダンスになります。

交流回路を考えていくためには虚数（ $j$ ）の計算はどうしても避けられないので、苦手な人は早めにおぼえておいた方がいいですよ。

といっても、虚数の計算って基本的に $j \times j = -1$ だけおぼえておけばだいたいOKなんですけどね。

他の回路についてもインピーダンスの計算をしていますので、それぞれ次のページを参考にしてみてください。
RL直列回路、RC直列回路、LC直列回路の合成インピーダンスはこちら
⇒　交流回路の合成インピーダンスの計算（素子が2個直列接続の場合）
RL並列回路、RC並列回路、LC並列回路の合成インピーダンスはこちら
⇒　交流回路の合成インピーダンスの計算（素子が2個並列接続の場合）
RLC直列回路の合成インピーダンスはこちら
⇒　交流回路の合成インピーダンスの計算（RLC直列回路）
RLC並列回路の合成インピーダンスはこちら
⇒　交流回路の合成インピーダンスの計算（RLC並列回路）

このページに掲載の各回路の電圧と電流の計算とベクトル図については、それぞれ次のページを参考にしてみてください。
抵抗だけの回路についてはこちら
⇒　交流回路の電圧と電流の計算とベクトル図（抵抗だけの回路）
コイルだけの回路についてはこちら
⇒　交流回路の電圧と電流の計算とベクトル図（コイルだけの回路）
コンデンサだけの回路についてはこちら
⇒　交流回路の電圧と電流の計算とベクトル図（コンデンサだけの回路）

複素アドミタンス　←BACK

NEXT→　交流回路の合成インピーダンスの計算（素子が2個直列接続の場合）

交流回路のインピーダンスの計算（素子が1個の場合）　関連ページ

インピーダンス: インピーダンスについて解説しています。交流回路での電圧と電流の比をインピーダンスといい、インピーダンスの大きさは、交流電流の流れにくさを表わします。インピーダンスの求め方や、インピーダンス三角形、インピーダンス角などについても解説していますので参考にしてみてください。
複素インピーダンス: 複素インピーダンスについて解説しています。複素数で表わされたインピーダンスを複素インピーダンスといい、複素インピーダンスの実部は抵抗、虚部はリアクタンスを表わします。いろいろな交流回路の複素インピーダンスの求め方などについても解説していますので参考にしてみてください。
アドミタンス: アドミタンスについて解説しています。インピーダンスの逆数をアドミタンスといい、アドミタンスの大きさは、交流電流の流れやすさを表わします。アドミタンスの求め方や、アドミタンス三角形、アドミタンス角などについても解説していますので参考にしてみてください。
複素アドミタンス: 複素アドミタンスについて解説しています。複素数で表わされたアドミタンスを複素アドミタンスといい、複素アドミタンスの実部はコンダクタンス、虚部はサセプタンスを表わします。いろいろな交流回路の複素アドミタンスの求め方などについても解説していますので参考にしてみてください。
交流回路の合成インピーダンスの計算（素子が2個直列接続の場合）: 素子（抵抗R、コイルL、コンデンサC）が2個直列接続された場合（RL直列回路、RC直列回路,LC直列回路）の合成インピーダンスを計算しています。LC直列回路の場合には、コイルLとコンデンサCのリアクタンスの大きさによって合成インピーダンスのベクトルの向きが変わるので気を付けましょう。
交流回路の合成インピーダンスの計算（素子が2個並列接続の場合）: 素子（抵抗R、コイルL、コンデンサC）が2個並列接続された場合（RL並列回路、RC並列回路,LC並列回路）の合成インピーダンスを計算しています。LC並列回路の場合は、条件によって合成インピーダンスのベクトルの向きが変わるので気を付けましょう。各合成インピーダンスのベクトル図も書いていますので、参考にしてみてください。
交流回路の合成インピーダンスの計算（RLC直列回路）: 素子（抵抗R、コイルL、コンデンサC）が3個直列接続された場合（RLC直列回路）の合成インピーダンスを計算しています。RLC直列回路の場合、コイルLとコンデンサCのリアクタンスの大きさが同じときには合成インピーダンスは抵抗Rだけになります。これはすごく大事なことなのでおぼえておきましょう！
交流回路の合成インピーダンスの計算（RLC並列回路）: 素子（抵抗R、コイルL、コンデンサC）が3個並列接続された場合（RLC並列回路）の合成インピーダンスを計算しています。RLC並列回路の場合、周波数が反共振周波数のときコイルLとコンデンサCの並列回路部分が解放状態と同じになるため、合成インピーダンスは抵抗Rだけになります。
RLC直列共振回路: RLC直列共振回路について解説しています。RLC直列共振回路はフィルタ回路など電気で幅広く応用されている回路ですので、共振周波数など基本的なことだけでもおぼえておくようにしましょう。
RLC並列共振回路: RLC並列共振回路について解説しています。RLC並列共振回路などの共振回路は電気で幅広く応用されている回路ですので、共振周波数など基本的なことだけでもおぼえておくようにしましょう。
正弦波交流波形の実効値はなぜ最大値÷√2か？: 正弦波交流波形の実効値を求めるときは最大値を√2で割ればいいですが、では、なぜ√2で割れば実効値になるのでしょうか？正弦波交流波形の実効値が最大値÷√2になることを計算で導いてみましたので参考にしてみてください。全波整流波形、半波整流波形、方形波、のこぎり波についても実効値を計算してみました。
なぜコイルに流れる電流の位相は電圧より90°遅れるのか？: コイルに流れる電流の位相は電圧よりも90°遅れますが、コイルの場合、なぜ電流が電圧よりも90°遅れ位相になるのかを計算で導いています。
なぜコンデンサに流れる電流の位相は電圧より90°進むのか？: コンデンサに流れる電流の位相は電圧よりも90°進みますが、コンデンサの場合、なぜ電流が電圧よりも90°進み位相になるのかを計算で導いています。
交流回路の電圧と電流の計算とベクトル図（抵抗だけの回路）: 正弦波交流電源に抵抗だけ接続されている交流回路の回路に流れる電流と、抵抗にかかる電圧の計算方法について解説しています。電圧と電流のベクトル図の描き方についても解説していますので、交流回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（コイルだけの回路）: 正弦波交流電源にコイルだけ接続されている交流回路の回路に流れる電流と、コイルにかかる電圧の計算方法について解説しています。電圧と電流のベクトル図の描き方についても解説していますので、交流回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（コンデンサだけの回路）: 正弦波交流電源にコンデンサだけ接続されている交流回路の回路に流れる電流と、コンデンサにかかる電圧の計算方法について解説しています。電圧と電流のベクトル図の描き方についても解説していますので、交流回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（RL直列回路）: RL直列回路（交流回路）の各素子にかかる電圧、直列接続全体にかかる電圧、位相差の計算方法について解説しています。RL直列回路の電圧と電流のベクトル図の描き方についても解説していますので、RL直列回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（RC直列回路）: RC直列回路（交流回路）の各素子にかかる電圧、直列接続全体にかかる電圧、位相差の計算方法について解説しています。RC直列回路の電圧と電流のベクトル図の描き方についても解説していますので、RC直列回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（RLC直列回路）: RLC直列回路（交流回路）の各素子にかかる電圧、直列接続全体にかかる電圧、位相差の計算方法について解説しています。RLC直列回路の電圧と電流のベクトル図の描き方についても解説していますので、RLC直列回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（RL並列回路）: RL並列回路（交流回路）の各素子に流れる電流、回路全体に流れる電流、位相差の計算方法について解説しています。RL並列回路の電圧と電流のベクトル図の描き方についても解説していますので、RL並列回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（RC並列回路）: RC並列回路（交流回路）の各素子に流れる電流、回路全体に流れる電流、位相差の計算方法について解説しています。RC並列回路の電圧と電流のベクトル図の描き方についても解説していますので、RC並列回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（LC並列回路）: LC並列回路（交流回路）の各素子に流れる電流と、回路全体に流れる電流の計算方法について解説しています。LC並列回路の電圧と電流のベクトル図の描き方についても解説していますので、LC並列回路の計算やベクトル図の描き方の参考にしてみてください。
交流回路の電圧と電流の計算とベクトル図（RLC並列回路）: RLC並列回路（交流回路）の各素子に流れる電流、回路全体に流れる電流、位相差の計算方法について解説しています。RLC並列回路の電圧と電流のベクトル図の描き方についても解説していますので、RLC並列回路の計算やベクトル図の描き方の参考にしてみてください。
RL直列回路の電圧と電流の計算（電源の電圧を基準にした場合）: RL直列回路の回路に流れる電流と各素子にかかる電圧を電源の電圧を基準にして計算していますので、RL直列回路の電圧と電流の計算方法の参考にしてみてください。
RC直列回路の電圧と電流の計算（電源の電圧を基準にした場合）: RC直列回路の回路に流れる電流と各素子にかかる電圧を電源の電圧を基準にして計算していますので、RC直列回路の電圧と電流の計算方法の参考にしてみてください。
RLC直列回路の電圧と電流の計算（電源の電圧を基準にした場合）: RLC直列回路の回路に流れる電流と各素子にかかる電圧を電源の電圧を基準にして計算していますので、RLC直列回路の電圧と電流の計算方法の参考にしてみてください。
交流回路の電力の計算（抵抗だけの回路）: 負荷が抵抗だけの場合の交流回路の電力（瞬時電力、平均電力）の計算方法（求め方）、電力の波形などについて解説しています。
交流回路の電力の計算（コイルだけの回路）: 負荷がコイルだけの場合の交流回路の電力（瞬時電力、平均電力）の計算方法（求め方）、電力の波形などについて解説しています。
交流回路の電力の計算（コンデンサだけの回路）: 負荷がコンデンサだけの場合の交流回路の電力（瞬時電力、平均電力）の計算方法（求め方）、電力の波形などについて解説しています。
交流回路の電力の計算（RL直列回路）: RL直列回路の電力（瞬時電力、平均電力）の計算方法（求め方）、電力の波形などについて解説しています。
交流回路の電力の計算（RC直列回路）: RC直列回路の電力（瞬時電力、平均電力）の計算方法（求め方）、電力の波形などについて解説しています。
有効・無効・皮相電力: 交流回路には「有効電力」「無効電力」「皮相電力」の3種類の電力があります。それぞれの電力の求め方と、3つの電力の関係について解説しています。
力率とは？（力率と電力の関係）: 交流回路の勉強をしていると「力率」がでてきますが、力率って何でしょうか？力率の式の表し方には色々ありますが、ここでは、力率と皮相電力、有効電力、無効電力の関係とその関係式などについて解説します。
力率とは？（力率と位相の関係）: 交流回路の勉強をしていると「力率(cosΘ)」がでてきますが、力率って何でしょうか？力率の式の表し方には色々ありますが、ここでは、位相と力率の関係について抵抗、コイル、コンデンサの回路を例に解説しています。
波形の実効値、平均値、最大値、波形率、波高率の求め方: 波形は色々ありますが、その波形の特性を表わす値として実効値、平均値、最大値、波形率、波高率などがあります。ここでは、波形の実効値、平均値、最大値、波形率、波高率の定義式、求め方について解説しています。
正弦波波形の実効値、平均値、最大値、波形率、波高率の計算方法: 波形は色々ありますが、その波形の特性を表わす値として実効値、平均値、最大値、波形率、波高率などがあります。ここでは、正弦波波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。
全波整流波形の実効値、平均値、最大値、波形率、波高率の計算方法: 波形は色々ありますが、その波形の特性を表わす値として実効値、平均値、最大値、波形率、波高率などがあります。ここでは、全波整流波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。
半波整流波形の実効値、平均値、最大値、波形率、波高率の計算方法: 半波整流波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。波形の特性を表わす値として実効値、平均値、最大値、波形率、波高率などがありますが、これらは大事な値ですので、求め方、計算方法をおぼえておきましょう。
方形波波形の実効値、平均値、最大値、波形率、波高率の計算方法: 方形波波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。方形波波形の場合、実効値と平均値と最大値が同じ値、波形率と波高率が同じ値になります。ちなみに、方形波と矩形波は同じです。
のこぎり波波形の実効値、平均値、最大値、波形率、波高率の計算方法: のこぎり波波形の実効値、平均値、最大値、波形率、波高率の計算方法、求め方について解説しています。のこぎり波波形の実効値と平均値を求めるためには、のこぎり波波形の式から考えないといけないので、他の波形よりも計算がちょっと大変です。
三相電力の公式はなぜ√3倍なのか？（三相電力の公式の導出）: 三相電力の公式はP＝√3VIcosφで表わされますが、なぜ√3倍になるのか？スター結線の場合とデルタ結線の場合それぞれについて、三相電力の公式を導出してみました。この三相電力の公式は電験三種の「理論」「電力」科目の問題を解くときに度々使われる基本的な公式ですのでおぼえておくようにしましょう。
スター結線（Y結線）の線間電圧はなぜ相電圧の√3倍になるのか？: スター結線（Y結線）されている三相交流回路の線間電圧は相電圧の√3倍になりますが、なぜ√3倍になるのか？スター結線のときの線間電圧と相電圧のベクトル図を求め、求めたベクトル図から√3倍になる理由について解説しています。
デルタスター変換（Δ→Y変換）: デルタスター変換（Δ→Y変換）について解説しています。デルタ結線（Δ結線）を等価なスター結線（Y結線）に変換するのをデルタスター変換（Δ→Y変換）といいます。デルタスター変換の式の導出方法についても解説していますので参考にしてみてください。
スターデルタ変換（Y→Δ変換）: スターデルタ変換（Y→Δ変換）について解説しています。スター結線（Y結線）を等価なデルタ結線（Δ結線）に変換するのをスターデルタ変換（Y→Δ変換）といいます。スターデルタ変換の式の導出方法についても解説していますので参考にしてみてください。
交流回路のテブナンの定理: 交流回路のテブナンの定理（鳳-テブナンの定理）について解説しています。テブナンの定理を使った交流回路の計算方法や、交流回路のテブナンの定理の証明についても解説していますので参考にしてみてください。

交流回路｜インピーダンスの計算（素子が1個の場合）