スポンサーリンク
直流回路の計算(分圧と分流)
※ページ内にPR・広告が含まれる場合があります。
直流回路の計算でおぼえておかなければならない分圧と分流について解説します。
またよく分からない言葉がでてきました。分圧…、分流…。
よく分からない言葉は、とりあえず想像して考えてみましょう。
分圧の「圧」はこれまでさんざん出てきた、電圧の圧なんじゃないかなぁー、と思ったりしますよね?(たぶん)
すると、分圧って、電圧を分けるとか、電圧が分けられるとか、そんなことを意味する言葉なんじゃないかな。と想像できます。
分流も同じような感じで想像してみると…。
分流の「流」はこれまで出てきた、電流の流なんじゃないかなぁー。と思ったりしますよね?(たぶん)
すると、分流って、電流を分けるとか、電流が分けられるとか、そんなことを意味する言葉なんじゃないかな。と想像できます。
実際のところ、分圧と分流はどんなものなのでしょうか?
これは、続きを読んでみると分かるので、もうちょっと読み進めてみましょう。
スポンサーリンク
分圧
次のように、電源に抵抗が2つ直列接続された回路を考えます。

ここで、電源の電圧を $V$[$\mathrm{V}$]、抵抗をそれぞれ $R_1$[$\Omega$]、$R_2$[$\Omega$]、抵抗 $R_1$ にかかる電圧を $V_1$[$\mathrm{V}$]、抵抗 $R_2$ にかかる電圧を $V_2$[$\mathrm{V}$]とします。
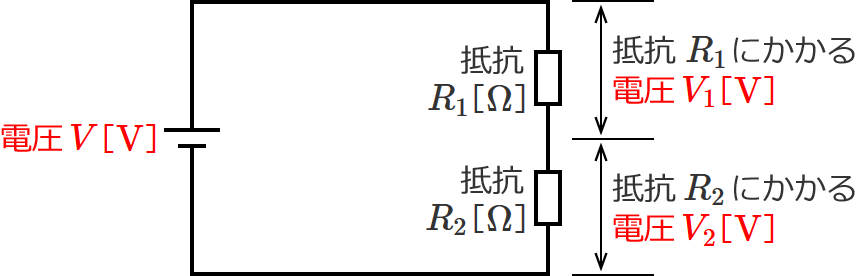
すると、キルヒホッフの電圧則(キルヒホッフの第二法則)より、抵抗 $R_1$ にかかる電圧 $V_1$[$\mathrm{V}$]と抵抗 $R_2$ にかかる電圧 $V_2$[$\mathrm{V}$]を足したものは、電源電圧 $V$[$\mathrm{V}$]になるのでした。つまり、式で書くと次のようになります。(キルヒホッフの電圧則そのままの話ですが…。)
$\therefore V=V_1+V_2$
キルヒホッフの電圧則(キルヒホッフの第二法則)について詳しくは、こちらのキルヒホッフの法則のページを参考にしてみてください。
この式をじ〜っとみると、電源電圧 $V$ は $V_1$ と $V_2$ を足したものに等しいので、つまり、電源電圧 $\boldsymbol{V}$ が $\boldsymbol{V_1}$ と $\boldsymbol{V_2}$ に分けられていると考えることができます。これが分圧です。
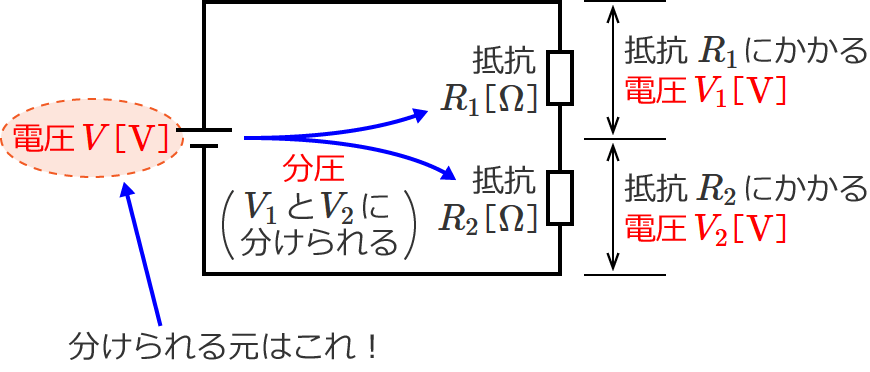
それでは次に、電圧 $\boldsymbol{V_1}$[$\boldsymbol{\mathrm{V}}$]と $\boldsymbol{V_2}$[$\boldsymbol{\mathrm{V}}$]の大きさを求めたいときはどうしたらいいでしょうか?
これは分圧の公式を使うと求めることができて、分圧の公式より、それぞれの電圧は次のように求められます。
$\therefore V_1=V\times\dfrac{R_1}{R_1+R_2}$ [$\mathrm{V}$] (←分圧の公式)
$\therefore V_2=V\times\dfrac{R_2}{R_1+R_2}$ [$\mathrm{V}$] (←分圧の公式)
分圧の公式(上の2つの式)を言葉で書くと、
求めたい分圧(電圧)= 電源の電圧 $\times\dfrac{\text{分圧を求めたいところの抵抗}}{\text{直列に接続されている抵抗の合計}}$
こんな感じになります。
式をみてみると、電源の電圧を抵抗の割合で分けていることが分かると思います。
分圧の公式は、第二種電気工事士学科試験の計算問題を解くときにけっこう使える公式ですので、上の2つの分圧の公式はおぼえておくようにしましょう。分圧の公式をおぼえておくと、電圧の計算が簡単になる場合もありますよ!
スポンサーリンク
スポンサーリンク
分流
次は、分流について解説します。
次のように、電源に抵抗が2つ並列接続された回路を考えます。
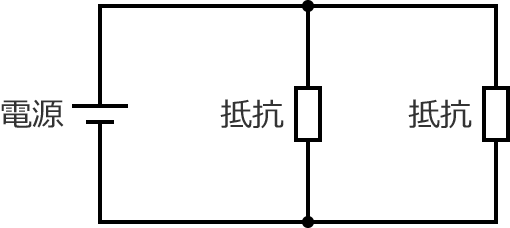
ここで、回路全体に流れる電流を $I$[$\mathrm{A}$]、抵抗をそれぞれ $R_1$[$\Omega$]、$R_2$[$\Omega$]、抵抗 $R_1$ に流れる電流を $I_1$[$\mathrm{A}$]、抵抗 $R_2$ に流れる電流を $I_2$[$\mathrm{A}$]とします。
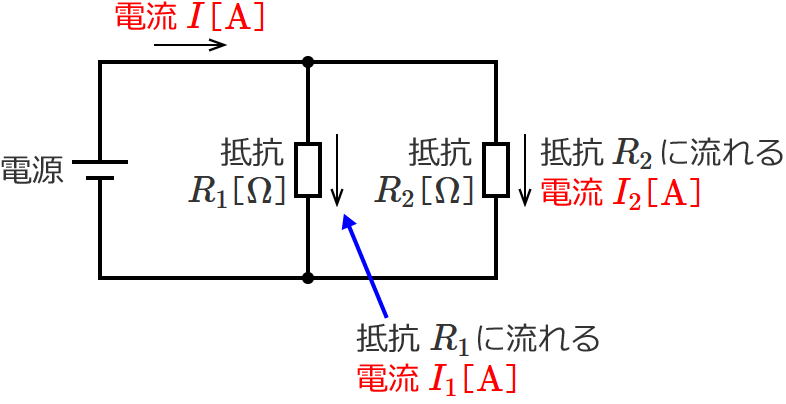
すると、キルヒホッフの電流則(キルヒホッフの第一法則)より、抵抗 $R_1$ に流れる電流 $I_1$[$\mathrm{A}$]と抵抗 $R_2$ に流れる電流 $I_2$[$\mathrm{A}$]を足したものは、回路全体に流れる電流 $I$[$\mathrm{A}$]になるのでした。つまり、式で書くと次のようになります。(キルヒホッフの電流則そのままの話ですが…。)
$\therefore I=I_1+I_2$
キルヒホッフの電流則(キルヒホッフの第一法則)について詳しくは、こちらのキルヒホッフの法則のページを参考にしてみてください。
分圧のときと同じように、この式をじ〜っとみると、回路全体に流れる電流 $I$ は $I_1$ と $I_2$ を足したものに等しいので、つまり、回路全体に流れる電流 $\boldsymbol{I}$ が $\boldsymbol{I_1}$ と $\boldsymbol{I_2}$ に分けられていると考えることができます。これが分流です。
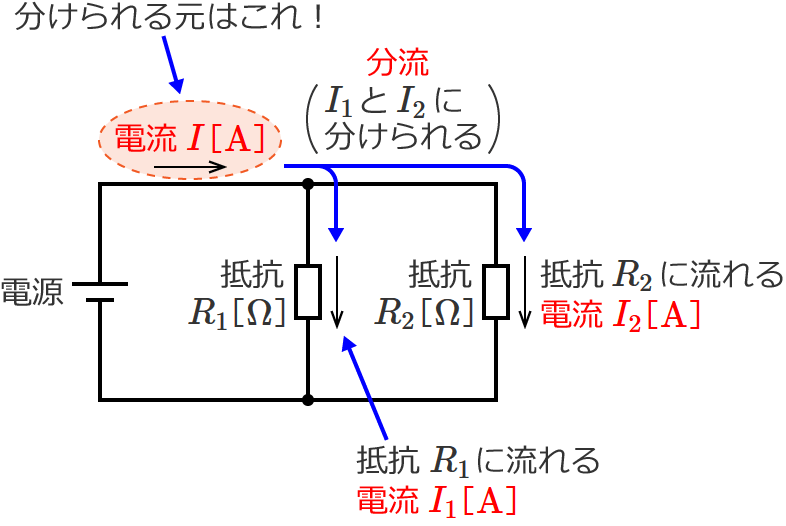
それでは次に、電流 $\boldsymbol{I_1}$[$\boldsymbol{\mathrm{A}}$]と $\boldsymbol{I_2}$[$\boldsymbol{\mathrm{A}}$]の大きさを求めたいときはどうしたらいいでしょうか?
これは分流の公式を使うと求めることができて、分流の公式より、それぞれの電流は次のように求められます。
$\therefore I_1=I\times\dfrac{R_2}{R_1+R_2}$ [$\mathrm{A}$] (←分流の公式)
$\therefore I_2=I\times\dfrac{R_1}{R_1+R_2}$ [$\mathrm{A}$] (←分流の公式)
分流の公式(上の2つの式)を言葉で書くと、
求めたい分流(電流)= 回路全体に流れる電流 $\times\dfrac{\text{分流を求めたいところではない抵抗}}{\text{並列に接続されている抵抗の合計}}$
こんな感じになります。
式をみてみると、回路全体に流れる電流を抵抗の割合で分けていることが分かると思います。
分圧の公式と分流の公式の分子の抵抗
分圧の公式と分流の公式の分子の抵抗は、「分圧の公式」と「分流の公式」で異なるので注意しましょう。
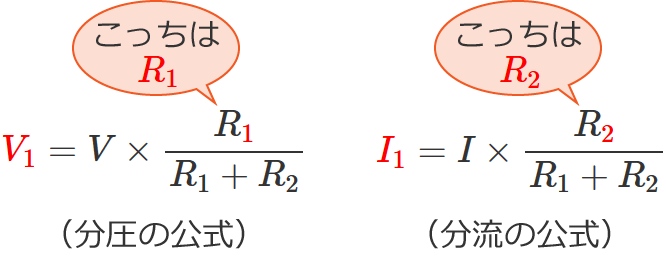
スポンサーリンク
スポンサーリンク
分圧の法則を使った直流回路の計算方法の例は分圧の法則による直流回路の計算のページ、分流の法則を使った直流回路の計算方法の例は分流の法則による直流回路の計算のページを参考にしてみてください。
分圧と分流を応用したものに倍率器と分流器があります。倍率器はこちらの倍率器のページ、分流器はこちらの分流器のページを参考にしてみてください。
直流回路の計算(基本) ←BACK
NEXT→ 電力・電力量・発熱量
スポンサーリンク
直流回路の計算(分圧と分流) 関連ページ
- 電圧・電流・抵抗
- 第二種電気工事士学科試験の「電気理論」の問題を解くためにおぼえておかなければならない「電圧・電流・抵抗」についてまとめています。「電圧・電流・抵抗」は電気の計算をするために一番初めに理解しておかなくてはならないとても重要な項目なので、しっかりと勉強しておきましょう。
- オームの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「オームの法則」についてまとめています。「オームの法則」は電気の計算をするときの一番基本的な法則になりますので、しっかり勉強しておきましょう。
- 電線の抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「電線の抵抗」についてまとめています。「電線の抵抗」は第二種電気工事士の学科試験でよく出題される重要な項目ですので、しっかり勉強しておきましょう。
- 直列接続と並列接続
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「直列接続と並列接続」についてまとめています。「直列接続と並列接続」は電気回路の基本になる接続方法です。
- 合成抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「合成抵抗」についてまとめています。第二種電気工事士の学科試験では、「合成抵抗」を求める問題がよく出題されています。
- キルヒホッフの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「キルヒホッフの法則」についてまとめています。「キルヒホッフの法則」は電気の計算をするときの重要な法則になりますので、しっかり勉強しておきましょう。
- 直流回路と交流回路
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路と交流回路」についてまとめています。交流回路の最大値と実効値の関係はとても重要で、学科試験でもたまに出題されています。
- 直流回路の計算(基本)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路の計算(基本)」についてまとめています。まずは簡単な直流回路の計算をできるようになりましょう。
- 電力・電力量・発熱量
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「電力・電力量・発熱量」についてまとめています。電力、電力量、発熱量の違いとそれぞれの求め方をおぼえましょう。
- 正弦波交流波形
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときにおぼえておかなければならない「正弦波交流波形」についてまとめています。「正弦波交流」の最大値または実効値を求める問題は試験でも度々出題されていますので、最大値と実効値の関係式は必ずおぼえておきましょう。
- 交流回路の位相
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路の位相」についてまとめています。「位相」は交流回路の計算をするときにとても重要な考え方です。遅れ位相、進み位相はどのようなものか理解しておきましょう。
- 交流回路のリアクタンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のリアクタンス」についてまとめています。コイルのリアクタンス(誘導性リアクタンス)とコンデンサのリアクタンス(容量性リアクタンス)の違いをおぼえておきましょう。
- 交流回路のインピーダンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のインピーダンス」についてまとめています。インピーダンスというとちょっとむずかしそうですが、おぼえると簡単です。
- 電気でよく使われる単位
- 第二種電気工事士学科試験の「電気理論」分野で出題される「電気でよく使われる単位」についてまとめています。「単位」は電気を勉強するときの基本中の基本になりますので、しっかりおぼえておきましょう。
- 電気でよく使われるギリシャ文字
- 第二種電気工事士学科試験の計算問題などや単位などで使用されるギリシャ文字の読み方と表わす意味についてまとめています。電気の世界に限らず理系の分野では、色々な量を表わしたり、単位の補助記号としてギリシャ文字が使用されますが、代表的なものだけでもおぼえておくようにしましょう。


