スポンサーリンク
電力・電力量・発熱量
※ページ内にPR・広告が含まれる場合があります。
電気機器を使う(動かす)ためには電力が必要で、その電力をどれくらい使ったかを表わすのが電力量です。また、電力を使うと電気機器には電流が流れるので、電気機器は発熱します。この発熱の量を表わすのが発熱量です。
このページでは、電力、電力量、発熱量について解説していますので、電力、電力量、発熱量の違いとそれぞれの求め方をおぼえましょう。
スポンサーリンク
電力
電圧 $V$[$\mathrm{V}$]の電源に抵抗 $R$[$\Omega$]が1つ接続されていて、回路に $I$[$\mathrm{A}$]の電流が流れている次のような回路を考えます。
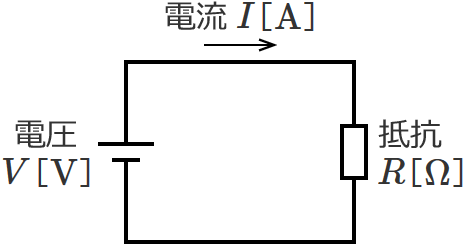
このとき、負荷(抵抗)が使う電力はいくらでしょうか?(負荷が使う電力は、負荷が消費する電力なので消費電力ともいいます。)
電力を求める式には色々あるのですが、もっとも基本的(?)な式は、電力=電圧×電流になります。電圧と電流をかけるだけです。
なので、この回路の場合の電力 $P$[$\mathrm{W}$]は、
$\therefore P=V\times I$ [$\mathrm{W}$]
となります。
電力の単位は「 $\mathrm{W}$ 」と書いて、「ワット」と読みます。
「ワット」って聞いたことありますよね?
「何ワットの電球買えばいいの?」
「30ワット!」
の「ワット」です。
電力を求める式には色々あると書きましたが、他にはどのような式があるのでしょうか?
電気のことを考えるときは、回路図をじ〜っとみて、しばらく「にらめっこ」していると、ハッ!!と気づくことがよくあります。
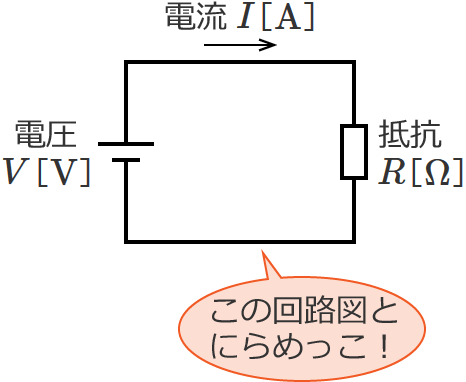
上に書いてある回路図は、これまでもよく登場してきた回路図です。どこに登場した回路図ですか?
あっちにもこっちにも登場していましたが、オームの法則のページにも登場していました。ということは、同じ回路図なので、ここでもオームの法則が成り立ちます!
オームの法則に電圧=電流×抵抗という式がありました。この式を電力の式に代入してみます。すると、
電力=電圧×電流=(電流×抵抗)× 電流=電流2×抵抗
$\therefore P=I^2\times R$ [$\mathrm{W}$]
となります。この式ももちろん電力の式になります。
では、もう一つ。
オームの法則に、 電流 $=\dfrac{\text{電圧}}{\text{抵抗}}$ という式もありました。これも電力の式に代入してみましょう。すると、
電力=電圧×電流=電圧 $\times \ \dfrac{\text{電圧}}{\text{抵抗}}$ $=\dfrac{\text{電圧}^2}{\text{抵抗}}$
$\therefore P=\dfrac{V^2}{R}$ [$\mathrm{W}$]
となります。
ね? 電力の式って色々あるでしょ。
以上、電力の式をまとめると、
$P=V\times I$ [$\mathrm{W}$]
$P=I^2\times R$ [$\mathrm{W}$]
$P=\dfrac{V^2}{R}$ [$\mathrm{W}$]
となります。
これら3つの式は、第二種電気工事士学科試験の計算問題を解くときにも度々使うので、公式としておぼえておくようにしましょう。
スポンサーリンク
スポンサーリンク
電力量
昔は、太陽光発電で発電した電気を「 $1\,\mathrm{kW\cdotp h}$(イチキロワットアワー)あたり $42$ 円で買い取り!」って、テレビや近所のおじさんがよく言ってましたよね?(最近はぜんぜん聞きませんけど…。)
この「 $1\,\mathrm{kW\cdotp h}$ 」というのが電力量のことで、電力量の単位「 $\mathrm{kW\cdotp h}$ 」を分解すると次のようになります。
「 $\mathrm{k}$ 」=「キロ」と読んで $1000$ 倍の意味。重さの $\mathrm{kg}$(キログラム)の「 $\mathrm{k}$(キロ)」と同じ。
「 $\mathrm{W}$ 」=「ワット」と読んで、前の項目の電力のこと。
「 $\mathrm{h}$ 」=「アワー」と読んで、時間の意味。($1$ 時間とか、$2$ 時間とかの「時間」)
つまり、この場合の電力量とは、何キロワットの電力を何時間発電したか?を表わすものになります。
例えば、$3\,\mathrm{kW}$ の電力を出力する太陽光パネルが $5$ 時間発電したとすると、このときの電力量(発電電力量)は、$3\,\mathrm{kW}\times 5\,\text{時間} =15\,\mathrm{kW\cdotp h}$ となります。
電力量の単位には「 $\mathrm{kW\cdotp h}$ 」の他に、「 $\mathrm{W\cdotp s}$ 」(ワット秒と読む)とか、「 $\mathrm{W\cdotp h}$ 」(ワットアワーと読む)があります。
「 $\mathrm{W\cdotp s}$ 」は、電力の単位が「 $\mathrm{W}$ 」で時間の単位が「 $\mathrm{s}$ 」(秒)なので、何ワットの電力を何秒発電したか?
「 $\mathrm{W\cdotp h}$ 」は、電力の単位が「 $\mathrm{W}$ 」で時間の単位が「 $\mathrm{h}$ 」(時間)なので、何ワットの電力を何時間発電したか?を表わすものになります。
ここで、初めの話に戻すと、「 $1\,\mathrm{kW\cdotp h}$(イチキロワットアワー)あたり $42$ 円で買い取り!」の意味は、$\boldsymbol{1\,\mathrm{kW}}$ の電力を $\boldsymbol{1}$ 時間 発電したら、$\boldsymbol{42}$ 円 で買っちゃうよ!ということになります。
そうそう、大事なことを忘れていました。電力量の式は、
電力量=電力×時間
となり、電力に時間(時間( $\mathrm{h}$ )または秒( $\mathrm{s}$ ))をかけたものになります。
発熱量
電気で動いているほとんどのものからは熱が発生します。(アッチ〜ですよ)
電源が入っているパソコン、照明、テレビ… さわってみると… やっぱり、アッチ〜ですよ!
なぜ電気で動いているものから熱が発生するのでしょうか?
それは、電流が流れるからなんです。
つまり、電流が熱の元になっているんです。
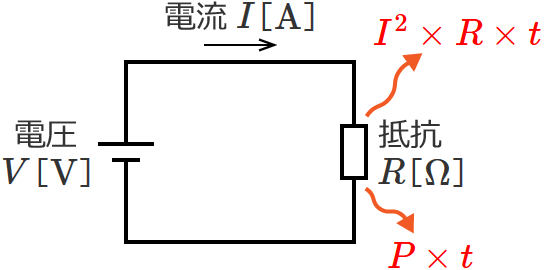
次のように、電圧 $V$[$\mathrm{V}$]の電源に $R$[$\Omega$]の抵抗が接続されている回路があるとして、回路には電流 $I$[$\mathrm{A}$]が流れているとします。
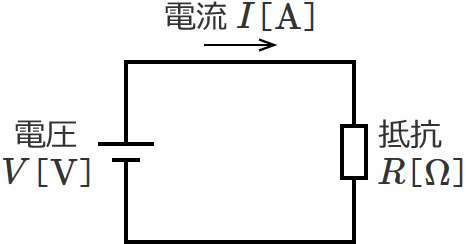
このとき、抵抗から発生する発熱量 $\boldsymbol{H}$[$\boldsymbol{\mathrm{J}}$]は、次の式で表わされます。
$\therefore H=I^2\times R\times t$ [$\mathrm{J}$]
$t$ は電流が流れた時間(秒)で、発熱量の単位は「 $\mathrm{J}$ 」と書いて、「ジュール」と読みます。
ねっ、この式で電流 $\boldsymbol{I}$ がゼロだったら $\boldsymbol{H=0}$ になるので、発熱がないでしょ?
また、発熱量は先ほどでてきた電力量に換算できて、
$\therefore 1$[$\mathrm{J}$]$=\,$$1$[$\mathrm{W\cdotp s}$] となります。
つまり、$1$[$\mathrm{J}$]という大きさの発熱量は $1$[$\mathrm{W\cdotp s}$]という大きさの電力量に等しいということです。
以上より、発熱量の式を整理すると、
$\therefore$ 発熱量 $H$[$\mathrm{J}$]$=$ 電流[$\mathrm{A}$]2 $\times$ 抵抗[$\Omega$]$\times$ 時間[$\mathrm{s}$]
$\therefore$ 発熱量 $H$[$\mathrm{J}$]$=$ 電力量[$\mathrm{W\cdotp s}$]
$\therefore$ 発熱量 $H$[$\mathrm{J}$]$=$ 電力[$\mathrm{W}$]$\times$ 時間[$\mathrm{s}$]
となります。
発熱量を電力量に換算するときは単位に注意!
発熱量[$\mathrm{J}$]を電力量に換算するときの電力量の単位は、[$\mathrm{W\cdotp h}$](ワットアワー)ではなく、[$\mathrm{W\cdotp s}$](ワット秒)であることに注意しましょう!
例えば、$7200000$[$\mathrm{J}$]を[$\mathrm{W\cdotp s}$]に換算するときは、そのまま
$7200000$[$\mathrm{J}$]$=7200000$[$\mathrm{W\cdotp s}$]になりますが、
$7200000$[$\mathrm{J}$]を[$\mathrm{W\cdotp h}$]に換算するときは、
$7200000$[$\mathrm{J}$]$=7200000$[$\mathrm{W\cdotp s}$]
$=7200000\div 3600$[$\mathrm{W\cdotp h}$] …①
$=2000$[$\mathrm{W\cdotp h}$]($=2$[$\mathrm{kW\cdotp h}$])
となります。
①で $3600$ で割っているのは、$1$ 時間は $60$ 分 $\times$ $60$ 秒 $=3600$ 秒になるためです。([$\mathrm{W\cdotp s}$]を[$\mathrm{W\cdotp h}$]に換算するときは $3600$ で割る!)
スポンサーリンク
スポンサーリンク
直流回路の計算(分圧と分流) ←BACK
NEXT→ 正弦波交流波形
スポンサーリンク
電力・電力量・発熱量 関連ページ
- 電圧・電流・抵抗
- 第二種電気工事士学科試験の「電気理論」の問題を解くためにおぼえておかなければならない「電圧・電流・抵抗」についてまとめています。「電圧・電流・抵抗」は電気の計算をするために一番初めに理解しておかなくてはならないとても重要な項目なので、しっかりと勉強しておきましょう。
- オームの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「オームの法則」についてまとめています。「オームの法則」は電気の計算をするときの一番基本的な法則になりますので、しっかり勉強しておきましょう。
- 電線の抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「電線の抵抗」についてまとめています。「電線の抵抗」は第二種電気工事士の学科試験でよく出題される重要な項目ですので、しっかり勉強しておきましょう。
- 直列接続と並列接続
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「直列接続と並列接続」についてまとめています。「直列接続と並列接続」は電気回路の基本になる接続方法です。
- 合成抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「合成抵抗」についてまとめています。第二種電気工事士の学科試験では、「合成抵抗」を求める問題がよく出題されています。
- キルヒホッフの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「キルヒホッフの法則」についてまとめています。「キルヒホッフの法則」は電気の計算をするときの重要な法則になりますので、しっかり勉強しておきましょう。
- 直流回路と交流回路
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路と交流回路」についてまとめています。交流回路の最大値と実効値の関係はとても重要で、学科試験でもたまに出題されています。
- 直流回路の計算(基本)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路の計算(基本)」についてまとめています。まずは簡単な直流回路の計算をできるようになりましょう。
- 直流回路の計算(分圧と分流)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「分圧」と「分流」についてまとめています。「分圧」と「分流」は電気回路の計算をするときの考え方の基本になります。
- 正弦波交流波形
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときにおぼえておかなければならない「正弦波交流波形」についてまとめています。「正弦波交流」の最大値または実効値を求める問題は試験でも度々出題されていますので、最大値と実効値の関係式は必ずおぼえておきましょう。
- 交流回路の位相
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路の位相」についてまとめています。「位相」は交流回路の計算をするときにとても重要な考え方です。遅れ位相、進み位相はどのようなものか理解しておきましょう。
- 交流回路のリアクタンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のリアクタンス」についてまとめています。コイルのリアクタンス(誘導性リアクタンス)とコンデンサのリアクタンス(容量性リアクタンス)の違いをおぼえておきましょう。
- 交流回路のインピーダンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のインピーダンス」についてまとめています。インピーダンスというとちょっとむずかしそうですが、おぼえると簡単です。
- 電気でよく使われる単位
- 第二種電気工事士学科試験の「電気理論」分野で出題される「電気でよく使われる単位」についてまとめています。「単位」は電気を勉強するときの基本中の基本になりますので、しっかりおぼえておきましょう。
- 電気でよく使われるギリシャ文字
- 第二種電気工事士学科試験の計算問題などや単位などで使用されるギリシャ文字の読み方と表わす意味についてまとめています。電気の世界に限らず理系の分野では、色々な量を表わしたり、単位の補助記号としてギリシャ文字が使用されますが、代表的なものだけでもおぼえておくようにしましょう。


