スポンサーリンク
オームの法則
※ページ内にPR・広告が含まれる場合があります。
電圧・電流・抵抗のページで「電圧」「電流」「抵抗」について解説しましたが、それぞれのイメージをつかめましたか?
このページではオームの法則について解説します。
スポンサーリンク
オームの法則(ちょっとその前に電圧・電流・抵抗のイメージ)
電圧・電流・抵抗のページの最後の方で、ちらっと「オームの法則」という言葉がでてきました。このオームの法則は、電圧と電流と抵抗の関係を表わすものですよということでした。
それでは、この関係ってどういう関係? ということになりますが、この関係について解説する前に、ここでもう一度、電圧・電流・抵抗のイメージをしっかり持っておきましょう。(これ、大事です!)
電圧・電流・抵抗の関係は、よくありがちですが「水」で例えられます。次の図のような水鉄砲を想像してみてください。(今時の若い方でも水鉄砲…、知ってますよね?)
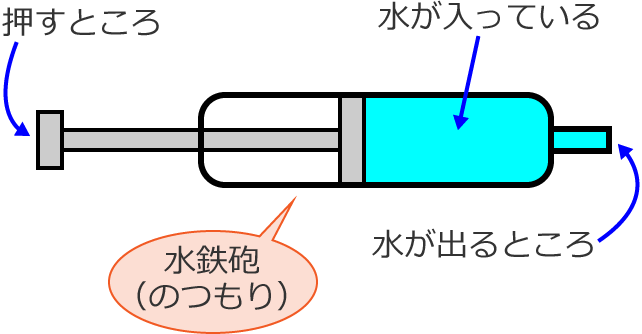
すいません、水鉄砲というより変な注射器になってしまいました。…が、これは水鉄砲です!
この水鉄砲を押してみましょう。すると当然ですが、水が出ます。
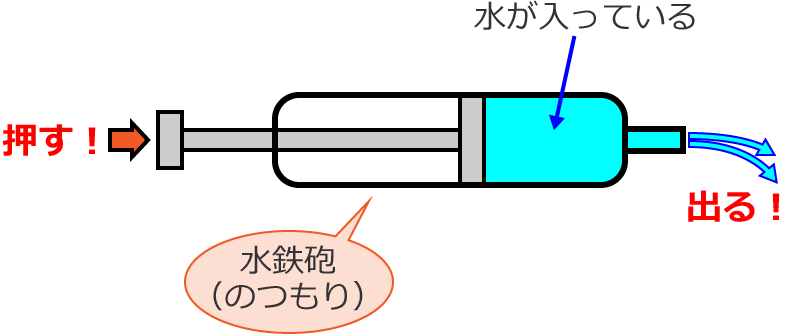
この
押す力が電圧
出てくる水の量が電流
になります。
そしてもう一つ、抵抗ですが、抵抗は「外部から加わる力に対して、はむかうもの。さからうもの。」でした。
水鉄砲が押されると水鉄砲から水が出ようとしますが、これにはむかおう(水が出るのをおさえよう)とするのは水鉄砲の出口の穴(の大きさ)です。なのでこの場合は、
水鉄砲の出口の穴の大きさが抵抗
になります。(水鉄砲の出口の穴が小さければ水(電流)はあまり出ず、穴が大きければ水(電流)はいっぱい出る。)
ただし、ここでの例え(水鉄砲)の場合、
出口の穴が大きい=抵抗が小さい
出口の穴が小さい=抵抗が大きい
となるので注意してください。
電圧、電流、抵抗が出揃ったので、ここで、より具体的に考えてみます。
抵抗の大きさが同じで電圧が大きい場合、電流はどうなるか?
抵抗の大きさが同じで電圧が大きい場合、電流はどうなるか? について水鉄砲で考えてみます。
次のように、出口の穴の大きさがどちらも同じ水鉄砲を考えます。
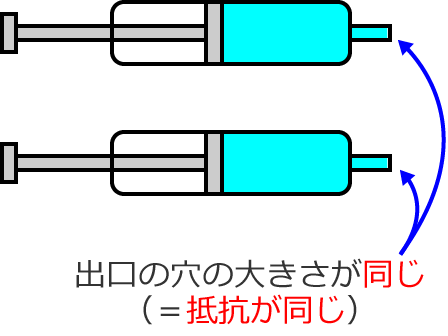
出口の穴の大きさが同じなので、この2つは抵抗が同じという意味になります。
このとき、上側の水鉄砲を弱く押して、下側の水鉄砲を強く押した場合、出てくる水の量はどうなりますか?
当然次のように、弱く押している上側の水鉄砲から出てくる水の量は少なく、強く押している下側の水鉄砲からは水がいっぱい出てきます。
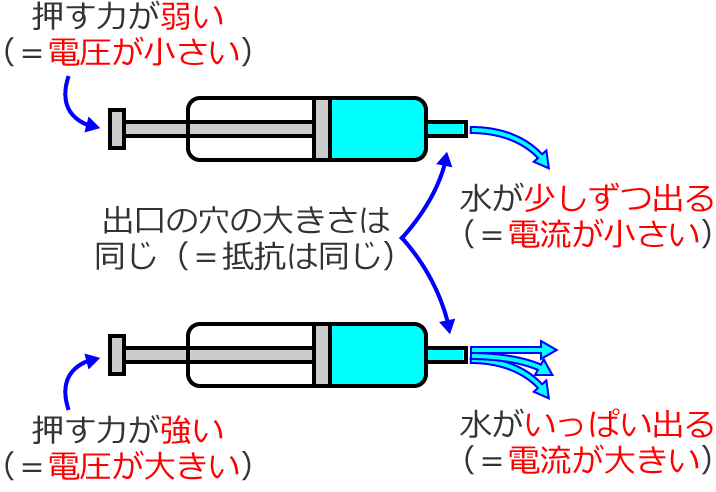
はい、これで、「抵抗(穴)の大きさが同じで電圧(押す力)が大きい場合、電流(水の量)はどうなるか?」の答えが分かりました。
答えは、抵抗の大きさが同じで電圧が大きい場合、電流は大きくなる!(抵抗の大きさが同じで電圧が小さい場合、電流は小さくなる。)ですね。
電圧の大きさが同じで抵抗が小さい場合、電流はどうなるか?
電圧の大きさが同じで抵抗が小さい場合、電流はどうなるか? について、また水鉄砲で考えてみます。
次のように、出口の穴の大きさが違う2つの水鉄砲を考えます。
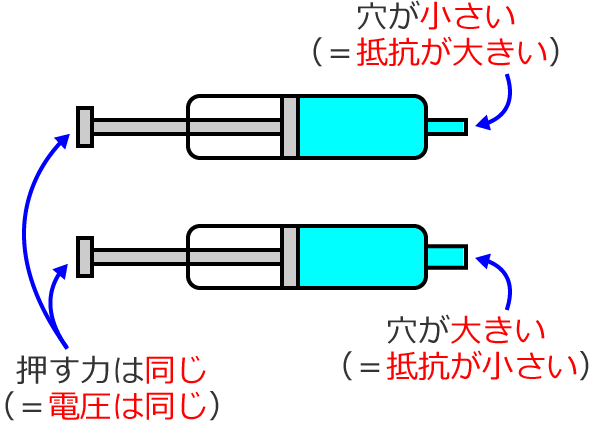
上側の水鉄砲の出口の穴は小さく、下側の水鉄砲の出口の穴は大きいので、上側は抵抗が大きく、下側は抵抗が小さいという意味になります。また、押す力はどちらも同じなので、電圧の大きさはどちらも同じということになります。
このとき、出てくる水の量はどうなりますか?
当然次のように、出口の穴が小さい上側の水鉄砲から出てくる水の量は少なく、出口の穴が大きい下側の水鉄砲からは水がいっぱい出てきます。
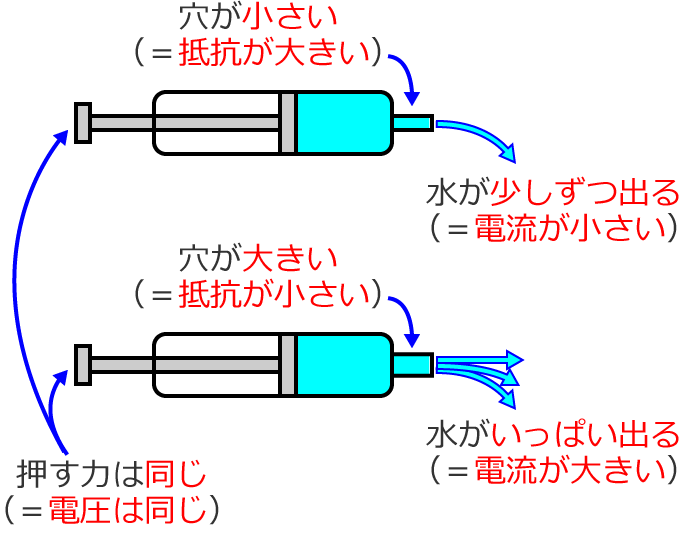
はい、これで、「電圧(押す力)の大きさが同じで抵抗が小さい(穴が大きい)場合、電流(水の量)はどうなるか?」の答えが分かりました。
答えは、電圧の大きさが同じで抵抗が小さい場合、電流は大きくなる!(電圧の大きさが同じで抵抗が大きい場合、電流は小さくなる。)ですね。
抵抗の大きさが違う場合に電流の大きさを同じにするためにはどうすれば良いか?
抵抗の大きさが違う場合に電流の大きさを同じにするためには、どうすれば良いか? について、またまた水鉄砲で考えてみます。
次のように、出口の穴の大きさが違う2つの水鉄砲を考えます。
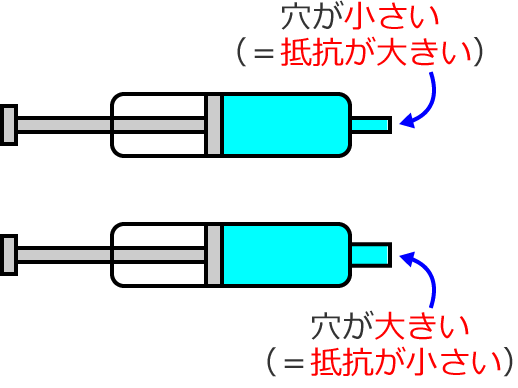
上側の水鉄砲の出口の穴は小さく、下側の水鉄砲の出口の穴は大きいので、上側は抵抗が大きく、下側は抵抗が小さいという意味になります。
このとき、出てくる水の量を同じにするためにはどうすればいいでしょうか?
つまり、抵抗が違う場合に電流を同じにするためにはどうすればいいでしょうか? ということです。
上側の水鉄砲の出口の穴は小さく、下側の水鉄砲の出口の穴は大きいので、上側の水鉄砲は強く押して、下側の水鉄砲は軽く押せばいいですよね?
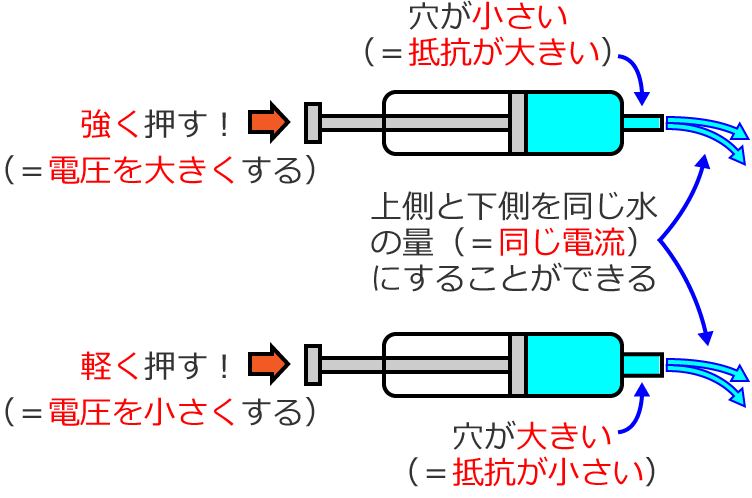
水鉄砲を押す力は「電圧」でしたので、これで「抵抗(穴)の大きさが違う場合に電流の大きさ(水の量)を同じにするためにはどうすればいいか?」の答えが分かりました。
答えは、抵抗が大きい方の電圧を大きくして、抵抗が小さい方の電圧を小さくすればいい!ですね。
スポンサーリンク
スポンサーリンク
オームの法則(もうちょっとその前に電気回路とは?)
オームの法則に入る前にもう一つ勉強しておかなければならないものがあります。
電気回路ってなんですか?
ということで(どういうこと??)、ここでは電気回路について勉強しましょう。
電気回路とは?
次のように電池とスイッチと電球があるとします。
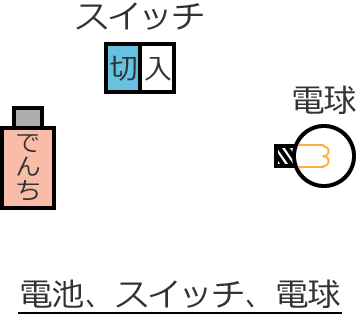
これは、電池とスイッチと電球が置いてあるだけなので電気回路とは言いません。
次に、電池とスイッチと電球を下図のように電線でつないでみます。(電線とは、電気を通すための線で、銅線などを使用します。)
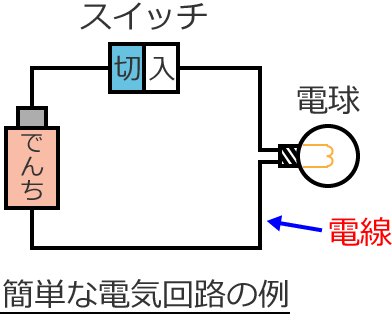
すると上図のようになりますが、この図のように、電池、スイッチ、電球などを電線で接続したものを電気回路と言います。
では、この電気回路のスイッチを入れるとどうなりますか?
もちろん、電球が点灯しますね。
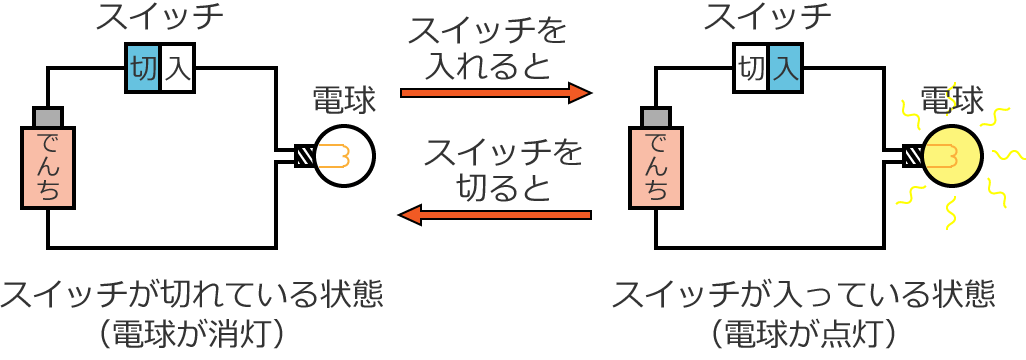
左側の図はスイッチが入っていないので電球は点灯していなく、右側の図はスイッチが入っているので電球が点灯しています。
スイッチを切れば電球が消灯して、スイッチを入れれば電球が点灯します。これは、ふつうにあたりまえのことです。
部屋の照明がついているのに、「あっ、スイッチが切れてる!」と言う人はいませんよね?
ではもう少し、この電気回路について考えてみましょう。
スイッチを入れると電球が点灯して、スイッチを切ると電球が消灯する
これは、みんな分かります。
では、なぜ、スイッチを入れると電球が点灯して、スイッチを切ると電球が消灯するのでしょうか?
ここでまず、電池について解説します。
「その電池何ボルト?」
「この電池1.5ボルト!」
この会話のように、電池のことを言う場合「○○ボルト」とみんな言っています。電圧・電流・抵抗のページで解説したように、「ボルト」とは「電圧の単位」でした。
なので、電池は電圧を発生するものということになります。
水鉄砲の例えでいえば、「水鉄砲を押す力を発生するもの」です。
水鉄砲を押すと水が出てきますが、「水」は電気でいえば「電流」ということでした。
すると、先ほどの電気回路でスイッチを入れたことで何がどうなっているか?
だいたい予想がつきますよね?
スイッチを入れたことで電気回路(電球)に電圧がかかり、電流が流れて電球が点灯した!(電流は水のようなものなので、スイッチが切れていると流れがせき止められ流れることができません。)
これが、「スイッチを入れると電球が点灯して、スイッチを切ると電球が消灯する」理由です。
電気回路とはどういうものか分かってもらえたでしょうか?
オームの法則(もうちょいその前に電気回路の書き方)
電気の話をするときは、ほとんどの場合、電気回路(電気回路図)を書いて話をします。
電気回路を書くときに、先ほどの電気回路の図のように書く方法もありますが、電池、スイッチ、電球などをいつも「絵」で書いていたら、電気回路を書くたびに、
疲れます!
時間がかかります!!
絵がヘタな人が書いたら、何の回路か分かりません!!!ということになります。
そこで、電気回路を書くときは、ふつう、電気用図記号というものを使って書きます。先ほどの電気回路を電気用図記号を使って書くと次の右図のようになります。
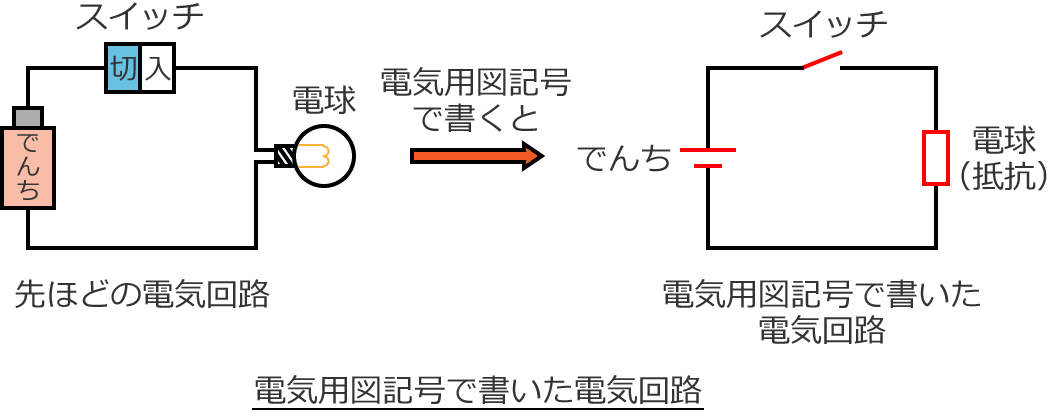
電池、スイッチ、電球(抵抗)はそれぞれ右図の赤で書いた記号になります。(ふだん書くときは黒で書いていいですよ。)
この赤で書いた記号が電気用図記号で、JISという規格の中でこのように書きなさい!と決められています。(「JIS」は日本産業規格(旧:日本工業規格)という規格で、「ジス」と読みます。)
したがって、仕事などで使うような電気回路を書くときは、必ずJISで決められたとおりの書き方で書かなければなりません。
このJISの電気用図記号を使って電気回路を書くと、絵で書くよりも、
疲れません!
時間がかかりません!!
絵がヘタな人が書いても、何の回路か分かります!!!ということになります。
ちょっと補足ですが、先ほどの右図の中で電球の下に「(抵抗)」と書いていますが、電球の実際の電気用図記号は○に×を書いたものになります。

ですが、ここではオームの法則について解説していく都合で、電球を抵抗として考えたいので抵抗の電気用図記号で書いています。
以上、ここでは、
- 電気回路を書くための「電気用図記号」というものがある
- 電気回路を書くときは「電気用図記号」を使う
ということをおぼえておいてください。
電気回路(回路図)の呼び方について
電気回路(回路図)の呼び方には色々あって、例えば次のようなものがあります。
- 電気回路
- 電気回路図
- 回路
- 回路図
オームの法則(いよいよ本題)
ここまでで、電圧、電流、抵抗、それから電気回路について解説してきました。
電圧・電流・抵抗には切っても切れない関係があって、この関係がどういうものか大体理解できたと思います。
それではいよいよオームの法則の本題に入ります。
まずはいきなりですが、オームの法則を式で表わすと次のようになります。
$\boldsymbol{V=I\times R}$ ←オームの法則の公式
$V$ って何? $I$ って何?? $R$ って何??? と思うかもしれませんが、$V$ 、$I$ 、$R$ はすでにここまでで勉強してきた電圧、電流、抵抗で、式で表わすために電圧を $V$ 、電流を $I$ 、抵抗を $R$ で表わしただけです。
次のように書いても、同じオームの法則を表わしています。
電圧=電流×抵抗
まずこの式の意味を理解してください。「式は苦手〜!」という方もいるかもしれませんが、式は言葉を記号で表わしたものと考えれば簡単です。
上の式に「=」がありますが、この「=」は、「=」の左側と右側は等しいですよ! というのを記号で表わしただけなので、
「電圧( $\boldsymbol{V}$ )」と「電流( $\boldsymbol{I}$ )に抵抗( $\boldsymbol{R}$ )をかけたもの」は等しい
という意味になります。
だんだん電気っぽくなってきました。電気の話をするときは、電気回路を書いて話をするんでしたね。ということで、電池とスイッチと抵抗が接続された次のような電気回路を考えます。
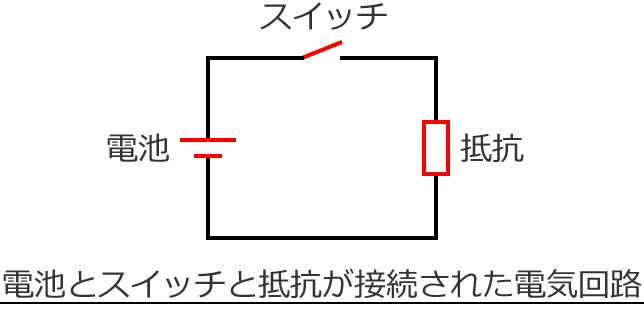
ここで、電池は「電圧を発生するもの」でしたので、この電池の電圧の大きさを $V$[$\mathrm{V}$]、抵抗は抵抗の記号「 $R$ 」を使ってその大きさを $R$[$\Omega$]とします。また、スイッチの記号は「 $\mathrm{Switch}$(スイッチ)」の頭文字を使って「 $\mathrm{S}$ 」とします。
すると上図の電気回路は、次のように書けます。
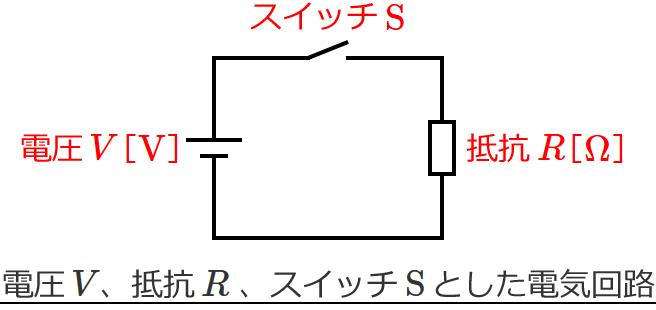
この場合スイッチ $\mathrm{S}$ が切れている状態なので、抵抗 $R$ に電圧はかかっていません。つまり、この回路には電流が流れていません。(水鉄砲は押さないと水がでませんよね? それと同じです。)
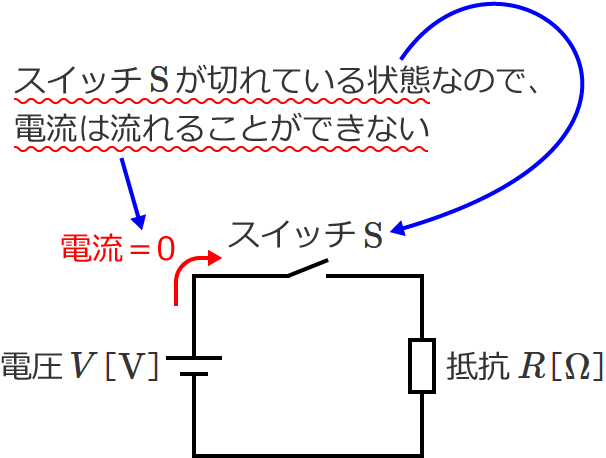
次に、スイッチ $\mathrm{S}$ を入れます。
スイッチ $\mathrm{S}$ を入れると、電池とスイッチと抵抗がグルっとつながるので電流が流れます。
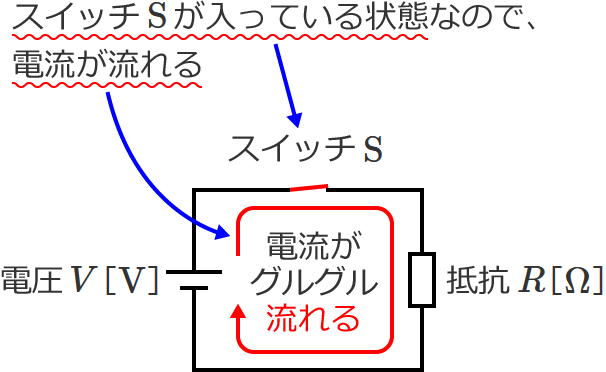
では、このとき、流れている電流の大きさは何アンペアですか?
これは、オームの法則を使うとすぐに求められます。(求め方は次の項目で解説します。)
それでは次に、電圧、電流、抵抗を求めるときにオームの法則をどのように使えばよいか?オームの法則の使い方について解説します。
オームの法則を使って「電圧」を求める
次のような電気回路があるとします。
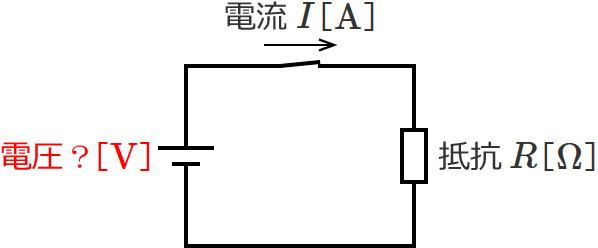
この電気回路では、電気回路に流れている電流が $I$[$\mathrm{A}$]で抵抗が $R$[$\Omega$]ということは分かっているのですが、電圧が何ボルトか分かりません。この分かっていない電圧をオームの法則で求めます。
オームの法則は、$V=I\times R$ で、「電流と抵抗をかけたものが電圧に等しい」という意味でした。これがそのまま答えになって、求める電圧は、
$\therefore$ 求める電圧 $=I\times R$ [$\mathrm{V}$]
となります。
あれ? 簡単ですね。
電流と抵抗が数値のときは、数値でそのまま計算すればOKです。例えば、次のように電流と抵抗が数値で与えられているとします。
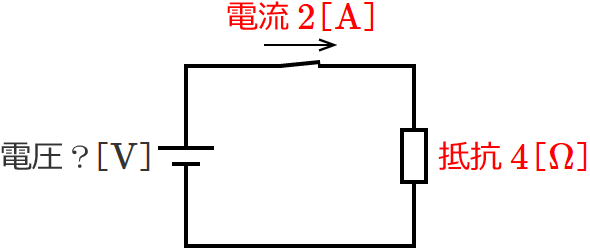
与えられた電流と抵抗の数値をオームの法則の式にあてはめればいいので、
求める電圧 $=2\times4 =8$
$\therefore$ 求める電圧 $=8$ [$\mathrm{V}$]
となります。
ただかけるだけですね。数字でも簡単です。
オームの法則を使って「電流」を求める
電圧と同じような感じで電流についても考えてみます。
次のような電気回路があるとします。
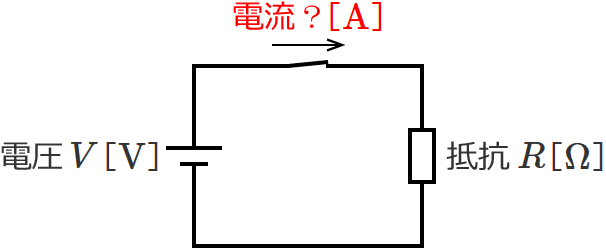
この電気回路では、電気回路(抵抗)にかかっている電圧が $V$[$\mathrm{V}$]で抵抗が $R$[$\Omega$]ということは分かっているのですが、流れている電流が何アンペアか分かりません。この分かっていない電流をオームの法則で求めます。
オームの法則は、$V=I\times R$ でした。
求めたいのは電流なので、オームの法則の式の両辺(「$=$」の左と右)を $R$ で割ります。すると、電流を求める式になります。
$I=\dfrac{V}{R}$
したがって、これがそのまま答えになって、求める電流は、
$\therefore$ 求める電流 $=\dfrac{V}{R}$ [$\mathrm{A}$]
となります。
オームの法則の式を電流の式に変形すればいいだけです。
電圧と抵抗が数値のときは、数値でそのまま計算すればOKです。例えば、次のように電圧と抵抗が数値で与えられているとします。
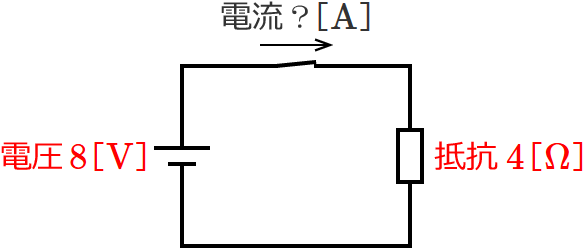
与えられた電圧と抵抗の数値をオームの法則の式( $V=I\times R$ )にあてはめればいいので、
$8=$(求める電流)$\times \ 4$ 、 求める電流 $=\dfrac{8}{4} =2$
$\therefore$ 求める電流 $=2$ [$\mathrm{A}$]
となります。
電圧を抵抗で割るだけですね。これも簡単ですね。
オームの法則を使って「抵抗」を求める
次は抵抗です。これも同じように考えていきます。
次のような電気回路があるとします。
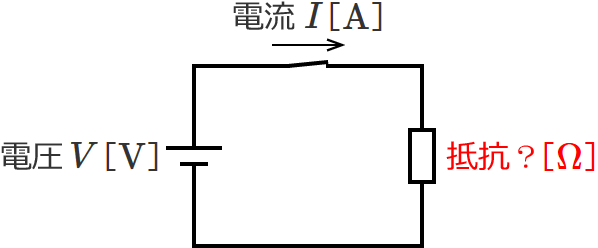
この電気回路では、電気回路(抵抗)にかかっている電圧が $V$[$\mathrm{V}$]で、流れている電流が $I$[$\mathrm{A}$]ということは分かっているのですが、抵抗が何オームか分かりません。この分かっていない抵抗をオームの法則で求めます。
オームの法則は、$V=I\times R$ でした。
求めたいのは抵抗なので、オームの法則の式の両辺(「=」の左と右)を $I$ で割ります。すると、抵抗を求める式になります。
$R=\dfrac{V}{I}$
したがって、これがそのまま答えになって、求める抵抗は、
$\therefore$ 求める抵抗 $=\dfrac{V}{I}$ [$\Omega$]
となります。
オームの法則の式を抵抗の式に変形すればいいだけです。
電圧と電流が数値のときは、数値でそのまま計算すればOKです。例えば、次のように電圧と電流が数値で与えられているとします。
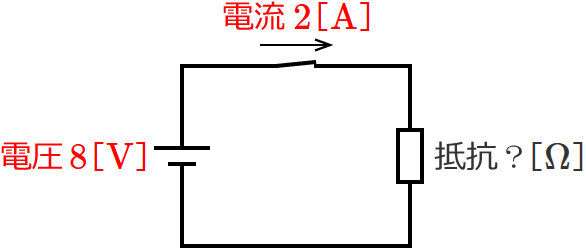
与えられた電圧と電流の数値をオームの法則の式( $V=I\times R$ )にあてはめればいいので、
$8=2 \ \times$(求める抵抗) 、 求める抵抗 $=\dfrac{8}{2} =4$
$\therefore$ 求める抵抗 $=4$ [$\Omega$]
となります。
電圧を電流で割るだけですね。
オームの法則のまとめ
最後に、オームの法則についてまとめておきます。
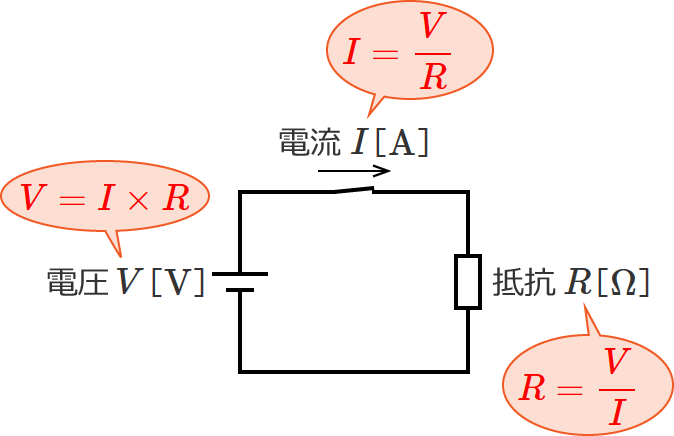
オームの法則は、
- 電圧、電流、抵抗の関係を表わしたもの
- 電圧=電流×抵抗
- 電流=電圧÷抵抗
- 抵抗=電圧÷電流
それから、
- 使ってみるといがいに簡単
オームの法則のおぼえ方
まとめまで書いておいて、なんなんですが、
「電流をかけて…」
「抵抗で割って…」
「電圧を…電流で割って…」
って、頭の中がごちゃごちゃしちゃう! という方のために、オームの法則のおぼえ方を紹介します。
小学校の算数の授業で、車などが移動したときの「距離(道のり)」「速さ」「時間」の求め方を習ったと思います。そのときに、次のようにするとおぼえられると教わりました。
まず、○に横棒と縦棒をひいて、その中に「き(距離の意味)」「は(速さの意味)」「じ(時間の意味)」と書きます。(「み(道のり)」「は」「じ」で習った方もいると思います。)
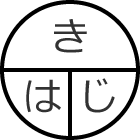
このとき、この「き・は・じ」の横棒は「÷」、縦棒は「×」を表わしているのでした。
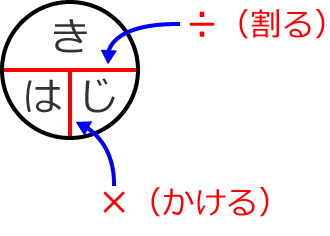
次に、求めたいものを指で隠します。例えば距離(道のり)を求めたいときは、
すると、「き」が隠されたので「は」と「じ」が残り、「は」と「じ」の間は縦棒なので、「き」を求めたいときは「は」と「じ」をかければいいということになります。
つまり、距離を求める式は、距離=速さ×時間ですよ。ということです。
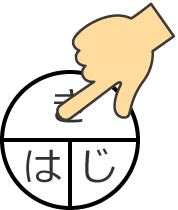
時間を求めたいときは、「じ」を隠せばいいので、
すると、「じ」が隠されたので「き」と「は」が残り、「き」と「は」の間は横棒なので、「じ」を求めたいときは「き」を「は」で割ればいいということになります。
つまり、時間を求める式は、時間=距離÷速さですよ。ということです。
この方法はオームの法則でも使えます!
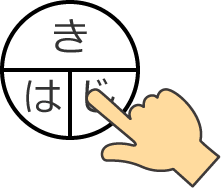
同じようにして、○に横棒と縦棒をひきます。そしてこの中に「 $V$(電圧)」「 $I$(電流)」「 $R$(抵抗)」と書きます。
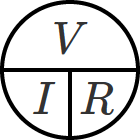
このとき、この「 $V$ 」「 $I$ 」「 $R$ 」の横棒は「÷」、縦棒は「×」を表わしています。(「き・は・じ」と同じです。)
あとは求めたいものを指で隠せばいいので、電圧を求めたいときは、

つまり、電圧を求める式は、電圧=電流×抵抗ということになります。
同じようにして、電流を求めたいときは「 $I$ 」を隠して、
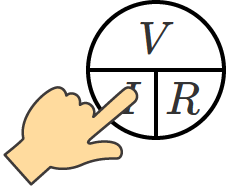
つまり、電流を求める式は、電流=電圧÷抵抗ということになります。
抵抗を求めたいときは「 $R$ 」を隠して、
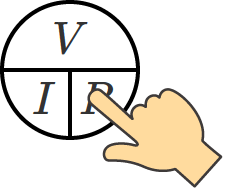
つまり、抵抗を求める式は、抵抗=電圧÷電流ということになります。
どうでしょう? これならおぼえやすいですよね。
スポンサーリンク
スポンサーリンク
スポンサーリンク
オームの法則 関連ページ
- 電圧・電流・抵抗
- 第二種電気工事士学科試験の「電気理論」の問題を解くためにおぼえておかなければならない「電圧・電流・抵抗」についてまとめています。「電圧・電流・抵抗」は電気の計算をするために一番初めに理解しておかなくてはならないとても重要な項目なので、しっかりと勉強しておきましょう。
- 電線の抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「電線の抵抗」についてまとめています。「電線の抵抗」は第二種電気工事士の学科試験でよく出題される重要な項目ですので、しっかり勉強しておきましょう。
- 直列接続と並列接続
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「直列接続と並列接続」についてまとめています。「直列接続と並列接続」は電気回路の基本になる接続方法です。
- 合成抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「合成抵抗」についてまとめています。第二種電気工事士の学科試験では、「合成抵抗」を求める問題がよく出題されています。
- キルヒホッフの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「キルヒホッフの法則」についてまとめています。「キルヒホッフの法則」は電気の計算をするときの重要な法則になりますので、しっかり勉強しておきましょう。
- 直流回路と交流回路
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路と交流回路」についてまとめています。交流回路の最大値と実効値の関係はとても重要で、学科試験でもたまに出題されています。
- 直流回路の計算(基本)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路の計算(基本)」についてまとめています。まずは簡単な直流回路の計算をできるようになりましょう。
- 直流回路の計算(分圧と分流)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「分圧」と「分流」についてまとめています。「分圧」と「分流」は電気回路の計算をするときの考え方の基本になります。
- 電力・電力量・発熱量
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「電力・電力量・発熱量」についてまとめています。電力、電力量、発熱量の違いとそれぞれの求め方をおぼえましょう。
- 正弦波交流波形
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときにおぼえておかなければならない「正弦波交流波形」についてまとめています。「正弦波交流」の最大値または実効値を求める問題は試験でも度々出題されていますので、最大値と実効値の関係式は必ずおぼえておきましょう。
- 交流回路の位相
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路の位相」についてまとめています。「位相」は交流回路の計算をするときにとても重要な考え方です。遅れ位相、進み位相はどのようなものか理解しておきましょう。
- 交流回路のリアクタンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のリアクタンス」についてまとめています。コイルのリアクタンス(誘導性リアクタンス)とコンデンサのリアクタンス(容量性リアクタンス)の違いをおぼえておきましょう。
- 交流回路のインピーダンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のインピーダンス」についてまとめています。インピーダンスというとちょっとむずかしそうですが、おぼえると簡単です。
- 電気でよく使われる単位
- 第二種電気工事士学科試験の「電気理論」分野で出題される「電気でよく使われる単位」についてまとめています。「単位」は電気を勉強するときの基本中の基本になりますので、しっかりおぼえておきましょう。
- 電気でよく使われるギリシャ文字
- 第二種電気工事士学科試験の計算問題などや単位などで使用されるギリシャ文字の読み方と表わす意味についてまとめています。電気の世界に限らず理系の分野では、色々な量を表わしたり、単位の補助記号としてギリシャ文字が使用されますが、代表的なものだけでもおぼえておくようにしましょう。


