スポンサーリンク
直流回路と交流回路
※ページ内にPR・広告が含まれる場合があります。
電気回路には、直流回路と交流回路があります。
「直流回路」と「交流回路」は何が違うの?
2つの回路の違いを説明する前に、まずは、それぞれの回路の例を書いてみます。左が直流回路、右が交流回路です。
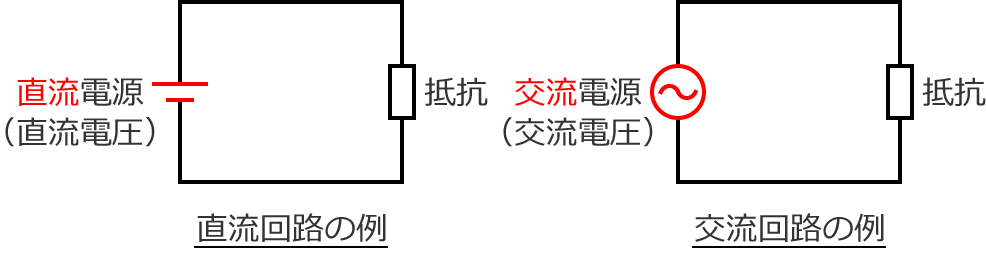
どちらの回路も電源に抵抗が接続されているだけの回路です。
違いは何ですか?
左と右の図をじ〜っと見くらべなくても分かりますね!
左の回路の電源は直流電源、右の回路の電源は交流電源になっています。
直流電源も交流電源もどちらも電圧を発生する電源ですが、電気の話をするときは、
- 直流電源によって発生する電圧を直流電圧
- 交流電源によって発生する電圧を交流電圧
と区別して使い分けることがよくあります。
また、電流についても、
- 直流電源(直流電圧)によって流れる電流を直流電流
- 交流電源(交流電圧)によって流れる電流を交流電流
と使い分けられます。
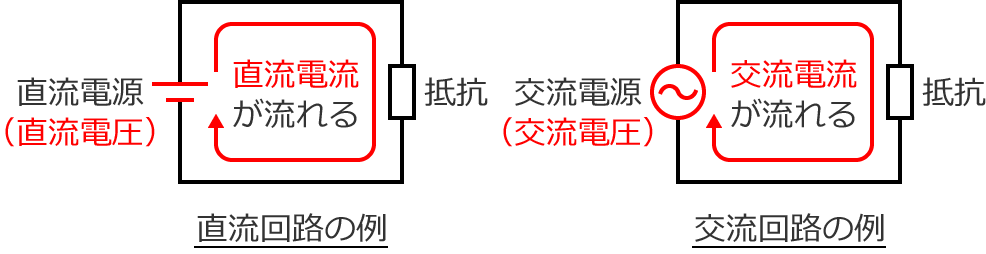
直流回路:直流電圧がかかって直流電流が流れる
交流回路:交流電圧がかかって交流電流が流れる
直流は「直流」、交流は「交流」です!
回路図だけ見くらべると、あまり変わりないように見えますが、電気的な意味合いではかなり違います!
この違いについては次の項目で解説します。
直流電源と交流電源を表わす記号
直流電源と交流電源を回路図に書くときは、次の図のように、直流電源は「横棒2本」で、交流電源は「○にニョロ」で書きます。

スポンサーリンク
もくじ
直流回路と交流回路の電気的な違い
前の項目で解説しましたが、
- 直流回路では、直流電圧がかかって直流電流が流れる
- 交流回路では、交流電圧がかかって交流電流が流れる
ということでした。
では次に、直流電圧、直流電流、交流電圧、交流電流について解説します。
直流電圧
直流電圧とは、ず〜っとプラスの電圧か、ず〜っとマイナスの電圧のことをいいます。
これについて、電圧波形で考えてみたいと思います。
電圧波形とは、横軸を時間、縦軸を電圧としてグラフで書いたもので、ず〜っと電圧の大きさが変わらない直流電圧は次のようなグラフになります。
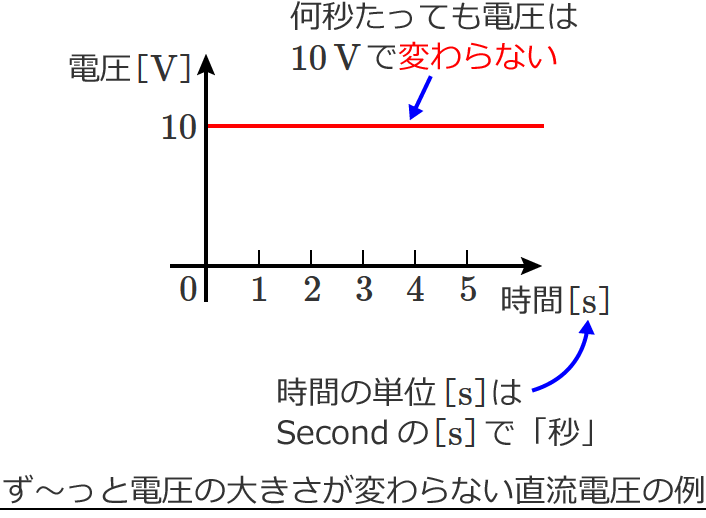
このグラフの見方は、横軸が時間なので、横軸を右方向に見ていくと、「1秒…2秒…3秒…、と時間が経過していきますよ」ということになり、縦軸の電圧は「時間の経過とともに電圧がこのように変化していきますよ」ということを表わしていると見ればいいです。
この電圧波形は、ず〜っとプラスの電圧($+10\,\mathrm{V}$)なので、直流電圧ということになります。
直流電流
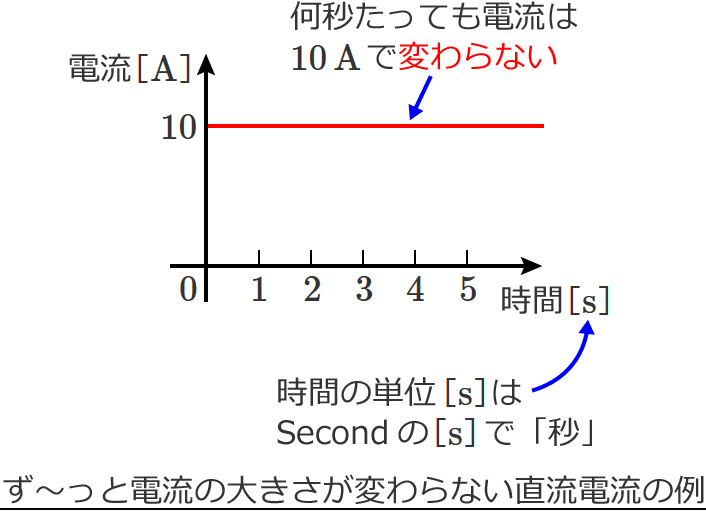
直流電流とは、ず〜っとプラスの電流か、ず〜っとマイナスの電流のことをいいます。
直流電圧と考え方は同じなので、直流電流波形の例だけ書いておきます。
スポンサーリンク
スポンサーリンク
交流電圧
交流電圧とは、プラスとマイナスを交互に繰り返す電圧のことをいいます。
つまり、時間の経過とともにプラスになったりマイナスになったりする電圧です。
交流電圧にも色々な種類がありますが、もっとも基本的で身近な交流電圧は、正弦波交流電圧です。
またよく分からない言葉がでてきました。正弦波? はっ? パッ?(正弦波は「せいげんは」と読みます。)
正弦波とは、数学の三角関数にでてくる関数の波形で、sin(サイン)、cos(コサイン)、tan(タンジェント)のうちの sin 関数の波形のことです。これ、苦手な方が多いですね。
sin(サイン)、cos(コサイン)、tan(タンジェント)については、こちらの三角関数のsin、cos、tanって何?のページを参考にしてみてください。
第二種電気工事士学科試験では、この三角関数をあまり深く知らなくても大丈夫なので、ちょっとだけ安心してください。ちょっとだけですよ。
ここでおぼえてほしいのは、
❶正弦波交流電圧の波形(グラフの形)
❷最大値
❸実効値
です。たったの3つなので必ずおぼえてください。
この3つは、第二種電気工事士学科試験でたまーに出題されています!
それでは、正弦波交流電圧の波形(グラフの形)、最大値、実効値の順に解説していきます。
正弦波交流電圧の波形(グラフの形)
正弦波交流電圧の波形(グラフの形)は、次のようになります。
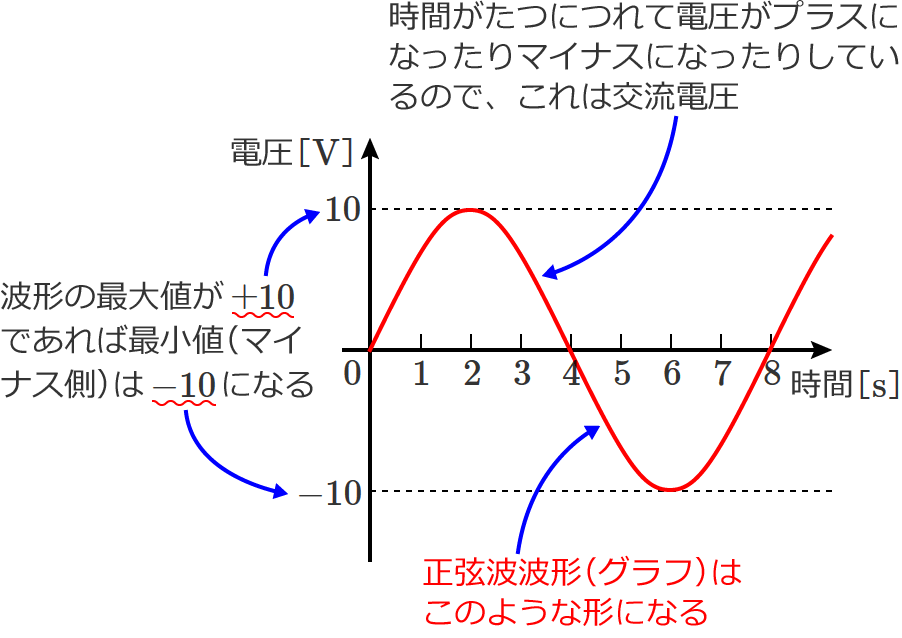
このように正弦波交流電圧の波形(グラフの形)は波のような形になり、この波がず〜っと続いていきます。
上図のグラフの横軸(時間)について
上図のグラフの横軸(時間)には $1$、$2$、$3$、$4$ …(つまり、$1$ 秒、$2$ 秒、$3$ 秒、$4$ 秒 …)と書いてあって、波 $1$ つ分で $8$ 秒になっていますが、例えば、みなさんがよく使っているコンセントの交流電圧の場合は、東日本では波 $1$ つ分で $0.02$ 秒、西日本では波1つ分で $0.0167$ 秒になります。
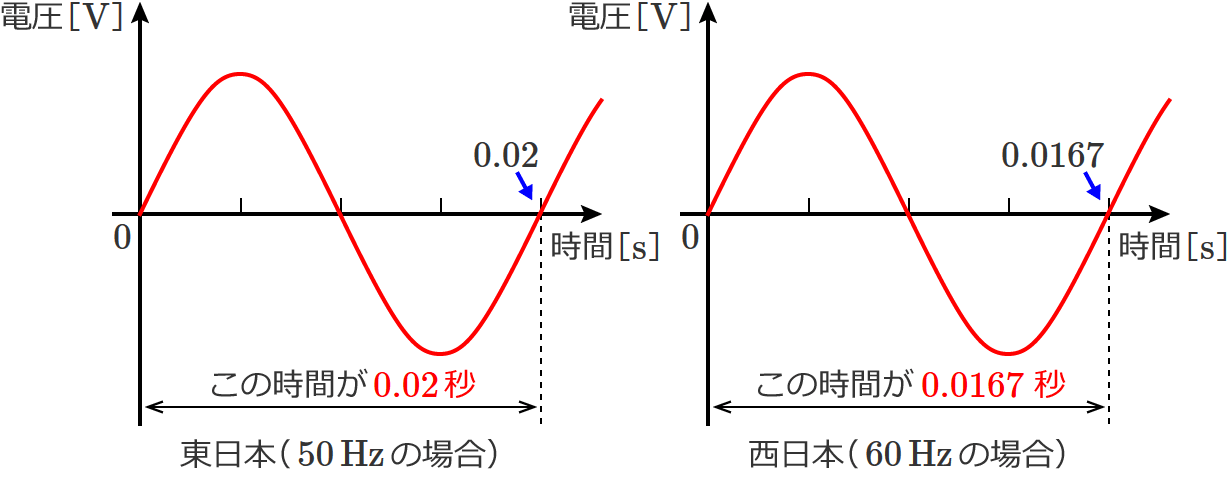
すごく短い時間の中でプラスとマイナスが繰り返されているのね!
正弦波交流電圧の最大値
前の項目の図の中にちょっと書いてしまいましたが、最大値は波形の一番上(頂点)の値になります。
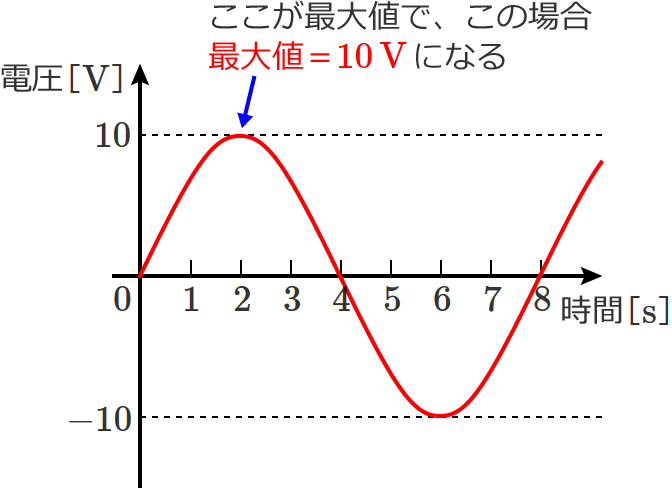
最大値は簡単ですね。電圧の最大のところが最大値になります。(そのままの言葉でそのままの意味)
正弦波交流電圧の実効値
おぼえてほしい3つのうちの最後は実効値です。
それでは、次の図の正弦波交流電圧の実効値を求めてみます。(図の正弦波交流電圧の最大値は「$1$」とします。)
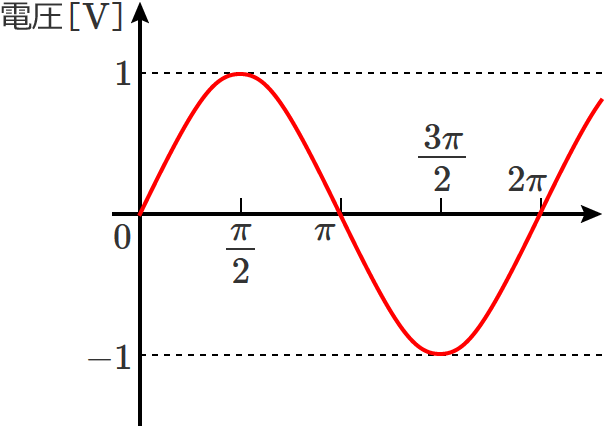
実効値を求めるときは、実効値を求めるための定義式を使って求めます。求める実効値を $V_{rms}$ とすると、
$V_{rms}=\sqrt{\dfrac{1}{2\pi}\displaystyle\int_0^{2\pi}\sin^2\omega t\,dt}$ $=\sqrt{\dfrac{1}{2\pi}\displaystyle\int_0^{2\pi}\dfrac{1-\cos 2\omega t}{2}\, dt}$
$=\sqrt{\dfrac{1}{4\pi}\displaystyle\int_0^{2\pi}\left( 1-\cos 2\omega t\right)\, dt}$ $=\sqrt{\dfrac{1}{4\pi}\left[ t-\dfrac{\sin 2\omega t}{2\omega}\right]_0^{2\pi}}$
$=\sqrt{\dfrac{1}{4\pi}\left( 2\pi -\dfrac{\sin\left( 2\omega\cdot 2\pi\right)}{2\omega} -0+\dfrac{\sin 0}{2\omega}\right)}$
$=\sqrt{\dfrac{1}{4\pi}\left( 2\pi\right)} =\sqrt{\dfrac{1}{2}} =\dfrac{1}{\sqrt{2}}$
$\therefore V_{rms}=\dfrac{1}{\sqrt{2}}$ となります。
この計算方法について詳しく知りたい方は、正弦波交流波形の実効値はなぜ最大値÷√2か?のページを参考にしてみてください。
げっ! なんだこの計算は?と思う方もいるかと思いますが、この計算方法については、第二種電気工事士学科試験では出題されません。
ここでおぼえておいてほしいのは、実効値はちゃんと計算されて求められているということです。
それから、いま求めた実効値は最大値が「$1$」の正弦波交流電圧のときの実効値でしたので、正弦波交流電圧の最大値と実効値の関係は、
実効値 $=\dfrac{\text{最大値}}{\sqrt{2}}$ …①
となります。
つまり、正弦波交流電圧の実効値を求めたいときは、正弦波交流電圧の最大値を $\boldsymbol{\sqrt{2}}$ で割るんですよ、ということです。
実効値は電気の分野で重要な項目で、特に正弦波交流の最大値と実効値の関係( $\boldsymbol{\sqrt{2}}$ で割るか $\boldsymbol{\sqrt{2}}$ をかけるか)は基本的なことなので、しっかりとおぼえておきましょう。
実効値から最大値を求める場合
①式より、$\text{最大値} =\sqrt{2}\times\text{実効値}$ となるので、実効値から最大値を求めるときは、実効値に $\sqrt{2}$ をかけます。
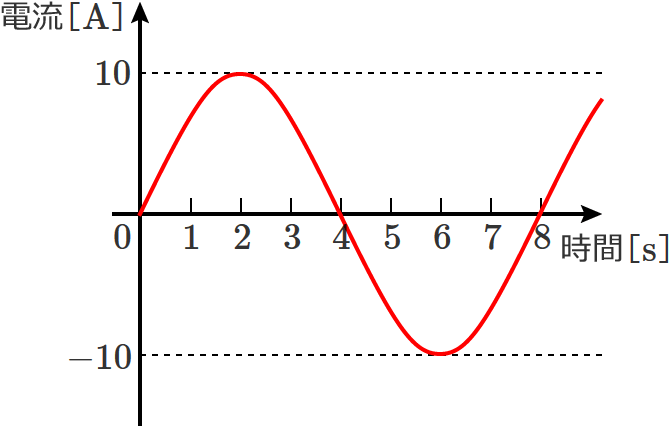
交流電流
交流電流とは、プラスとマイナスを交互に繰り返す電流のことをいいます。
つまり、時間の経過とともにプラスになったりマイナスになったりする電流です。
交流電圧と考え方は同じなので、正弦波交流電流波形の例だけ書いておきます。
スポンサーリンク
スポンサーリンク
正弦波交流電圧については、正弦波交流波形のページでもう少しくわしく解説していますので参考にしてみてください。
キルヒホッフの法則 ←BACK
NEXT→ 直流回路の計算(基本)
スポンサーリンク
直流回路と交流回路 関連ページ
- 電圧・電流・抵抗
- 第二種電気工事士学科試験の「電気理論」の問題を解くためにおぼえておかなければならない「電圧・電流・抵抗」についてまとめています。「電圧・電流・抵抗」は電気の計算をするために一番初めに理解しておかなくてはならないとても重要な項目なので、しっかりと勉強しておきましょう。
- オームの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「オームの法則」についてまとめています。「オームの法則」は電気の計算をするときの一番基本的な法則になりますので、しっかり勉強しておきましょう。
- 電線の抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「電線の抵抗」についてまとめています。「電線の抵抗」は第二種電気工事士の学科試験でよく出題される重要な項目ですので、しっかり勉強しておきましょう。
- 直列接続と並列接続
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「直列接続と並列接続」についてまとめています。「直列接続と並列接続」は電気回路の基本になる接続方法です。
- 合成抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「合成抵抗」についてまとめています。第二種電気工事士の学科試験では、「合成抵抗」を求める問題がよく出題されています。
- キルヒホッフの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「キルヒホッフの法則」についてまとめています。「キルヒホッフの法則」は電気の計算をするときの重要な法則になりますので、しっかり勉強しておきましょう。
- 直流回路の計算(基本)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路の計算(基本)」についてまとめています。まずは簡単な直流回路の計算をできるようになりましょう。
- 直流回路の計算(分圧と分流)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「分圧」と「分流」についてまとめています。「分圧」と「分流」は電気回路の計算をするときの考え方の基本になります。
- 電力・電力量・発熱量
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「電力・電力量・発熱量」についてまとめています。電力、電力量、発熱量の違いとそれぞれの求め方をおぼえましょう。
- 正弦波交流波形
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときにおぼえておかなければならない「正弦波交流波形」についてまとめています。「正弦波交流」の最大値または実効値を求める問題は試験でも度々出題されていますので、最大値と実効値の関係式は必ずおぼえておきましょう。
- 交流回路の位相
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路の位相」についてまとめています。「位相」は交流回路の計算をするときにとても重要な考え方です。遅れ位相、進み位相はどのようなものか理解しておきましょう。
- 交流回路のリアクタンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のリアクタンス」についてまとめています。コイルのリアクタンス(誘導性リアクタンス)とコンデンサのリアクタンス(容量性リアクタンス)の違いをおぼえておきましょう。
- 交流回路のインピーダンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のインピーダンス」についてまとめています。インピーダンスというとちょっとむずかしそうですが、おぼえると簡単です。
- 電気でよく使われる単位
- 第二種電気工事士学科試験の「電気理論」分野で出題される「電気でよく使われる単位」についてまとめています。「単位」は電気を勉強するときの基本中の基本になりますので、しっかりおぼえておきましょう。
- 電気でよく使われるギリシャ文字
- 第二種電気工事士学科試験の計算問題などや単位などで使用されるギリシャ文字の読み方と表わす意味についてまとめています。電気の世界に限らず理系の分野では、色々な量を表わしたり、単位の補助記号としてギリシャ文字が使用されますが、代表的なものだけでもおぼえておくようにしましょう。


