スポンサーリンク
交流回路のリアクタンス
※ページ内にPR・広告が含まれる場合があります。
交流回路ではリアクタンスというものがでてきます。
リアクタンスには、「誘導性リアクタンス」と「容量性リアクタンス」があって、コイルのリアクタンスは誘導性リアクタンス、コンデンサのリアクタンスは容量性リアクタンスになります。
それで、リアクタンスってなんですか?ということになりますが、
リアクタンスとは、電流を妨げる大きさ、つまり電流の通しにくさを表わしたものになります。
あれ?似ているものがありました、抵抗!
抵抗も「電流の通しにくさ」を表わすものでした。抵抗はオームの法則のページでも解説しましたが、ちょっとおさらいすると次のような式でした。
$R$(抵抗)$=\dfrac{V\text{(電圧)}}{I\text{(電流)}}$ [$\Omega$]
すると、リアクタンスも抵抗と同じように「電流を妨げる大きさ」を表わすものなので、リアクタンスを $X$[$\Omega$]とするとリアクタンスの式は、
$\therefore X$(リアクタンス)$=\dfrac{V\text{(電圧)}}{I\text{(電流)}}$ [$\Omega$]
と表わされます。
なので、へー、抵抗もリアクタンスも式は同じですねー。ということになります。
先ほど、リアクタンスには「誘導性リアクタンス」と「容量性リアクタンス」があって、コイルのリアクタンスは誘導性リアクタンス、コンデンサのリアクタンスは容量性リアクタンスとお話ししました。
それでは次に、「コイルのリアクタンス(誘導性リアクタンス)」と「コンデンサのリアクタンス(容量性リアクタンス)」について解説します。
スポンサーリンク
コイルのリアクタンス(誘導性リアクタンス)
コイルのリアクタンスは誘導性リアクタンスで、リアクタンスは、電流を妨げる大きさを表わすものでしたので、コイルのリアクタンス(誘導性リアクタンス)を $X_L$[$\Omega$]として回路図で書いてみると次のような意味になります。
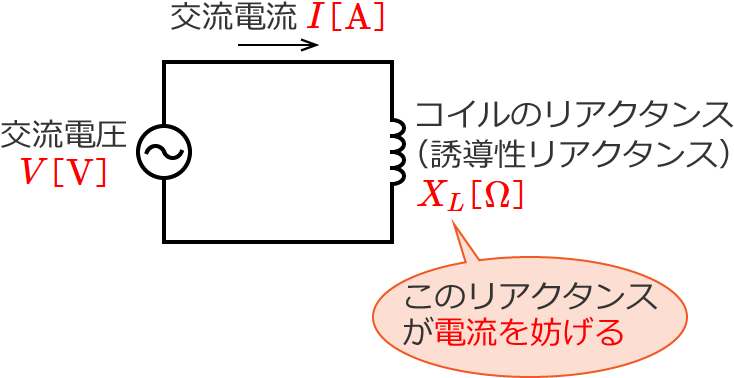
式で書くと次のようになります。
$\therefore X_L=\dfrac{V}{I}$ [$\Omega$]
この式を電流の式に書きかえると、
$\therefore I=\dfrac{V}{X_L}$ [$\mathrm{A}$] …① となるので、
コイルのリアクタンス $X_L$ が大きくなると電流 $I$ は小さくなって、コイルのリアクタンス $X_L$ が小さくなると電流 $I$ は大きくなることが分かります。(コイルに流れる電流 $I$ は、コイルのリアクタンス $X_L$ に反比例します。)
ここまでみるとコイルのリアクタンスは抵抗と何も変わらないように思えますが、このコイルのリアクタンスは周波数で大きさが変わるんです。
コイルのリアクタンス $X_L$[$\Omega$] は、電源の周波数を $f$[$\mathrm{Hz}$]、コイルのインダクタンスを $L$[$\mathrm{H}$](単位の「 $\mathrm{H}$ 」はヘンリーと読む)とすると次の式で表わされます。
$\therefore X_L=2\pi fL$ [$\Omega$] …②
この式から、周波数 $\boldsymbol{f}$ が大きくなるとコイルのリアクタンス $\boldsymbol{X_L}$ が大きくなることが分かります。(コイルのリアクタンス $X_L$ は、周波数 $f$ に比例します。)
ね? 抵抗と違ってちょっとやっかいでしょ?
ちなみに、②を①式に代入すると、
$I=\dfrac{V}{X_L} =\dfrac{V}{2\pi fL}$
$\therefore I=\dfrac{V}{2\pi fL}$ [$\mathrm{A}$] となるので、
コイルのインダクタンス $L$ が変わらなくても、周波数 $f$ が大きくなるとコイルのリアクタンス $X_L$ が大きくなるので電流 $I$ は小さくなります。
さらに、やっかい!
交流回路を勉強していると、この辺りから挫折する方が多いのですが、頑張っておぼえましょう!
第二種電気工事士の学科試験の問題は、公式をおぼえておく程度でも解ける問題は多いので、公式だけでもね。
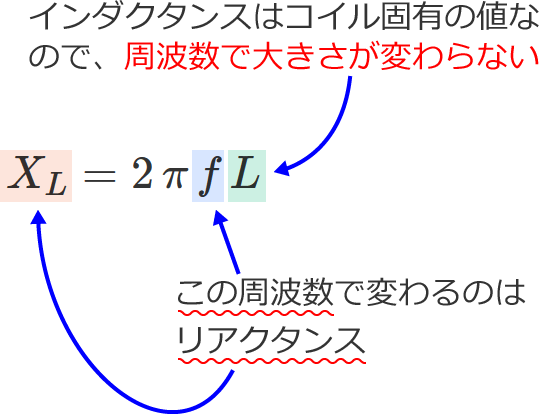
インダクタンスは周波数で変わらない、リアクタンスは周波数で変わる
コイルのインダクタンス $L$ の値は、コイルの固有の値(つまり、コイルごとに決まる値)です。なので、電源の周波数 $f$ が変わったとしても、インダクタンス $L$ の値は変わりません。
ですが、リアクタンス $X_L$ は、$X_L=2\pi fL$ なので、電源の周波数 $f$ によりその大きさが変わります。
インダクタンス $L$ とリアクタンス $X_L$ を混同しないように注意しましょう。
スポンサーリンク
スポンサーリンク
コンデンサのリアクタンス(容量性リアクタンス)
次は、コンデンサのリアクタンスです。コイルのリアクタンスと同じように説明していきます。
コンデンサのリアクタンスは容量性リアクタンスで、リアクタンスは、電流を妨げる大きさを表わすものでしたので、コンデンサのリアクタンス(容量性リアクタンス)を $X_C$[$\Omega$]として回路図で書いてみると次のような意味になります。
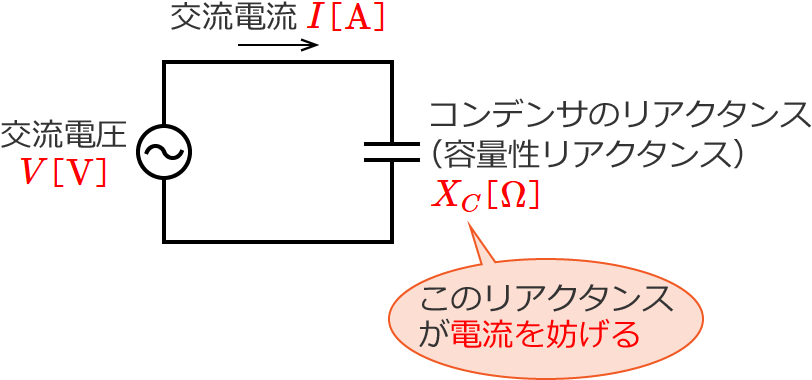
式で書くと次のようになります。
$\therefore X_C=\dfrac{V}{I}$ [$\Omega$]
この式を電流の式に書きかえると、
$\therefore I=\dfrac{V}{X_C}$ [$\mathrm{A}$] …③ となるので、
コンデンサのリアクタンス $X_C$ が大きくなると電流 $I$ は小さくなって、コンデンサのリアクタンス $X_C$ が小さくなると電流 $I$ は大きくなることが分かります。コイルのリアクタンスと同じです。(コンデンサに流れる電流 $I$ は、コンデンサのリアクタンス $X_C$ に反比例します。)
このコンデンサのリアクタンスもコイルのリアクタンスと同じように、周波数で大きさが変わるんです。
コンデンサのリアクタンス $X_C$[$\Omega$]は、電源の周波数を $f$[$\mathrm{Hz}$]、コンデンサの静電容量を $C$[$\mathrm{F}$](単位の「 $\mathrm{F}$ 」はファラドと読む)とすると次の式で表わされます。
$\therefore X_C=\dfrac{1}{2\pi fC}$ [$\Omega$] …④
この式から、周波数 $\boldsymbol{f}$ が大きくなるとコンデンサのリアクタンス $\boldsymbol{X_C}$ が小さくなることが分かります。(コンデンサのリアクタンス $X_C$ は、周波数 $f$ に反比例します。)
あれ?コイルのリアクタンスとは反対になりました。
ちなみに、④を③式に代入すると、
$I=\dfrac{V}{X_C} =\dfrac{V}{\dfrac{1}{2\pi fC}} =2\pi fCV$
$\therefore I=2\pi fCV$ [$\mathrm{A}$] となるので、
コンデンサのリアクタンスの場合は、周波数 $f$ が大きくなると電流 $I$ も大きくなります。
これまたコイルのリアクタンスと反対です。
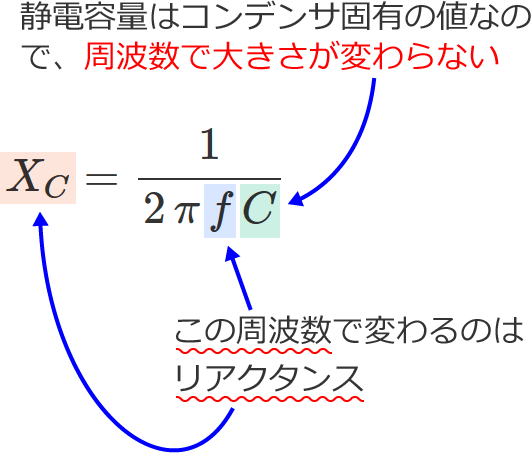
静電容量は周波数で変わらない、リアクタンスは周波数で変わる
コンデンサの静電容量 $C$ の値は、コンデンサの固有の値(つまり、コンデンサごとに決まる値)です。なので、電源の周波数 $f$ が変わったとしても、静電容量 $C$ の値は変わりません。
ですが、リアクタンス $X_C$ は、$X_C=\dfrac{1}{2\pi fC}$ なので、電源の周波数 $f$ によりその大きさが変わります。
リアクタンスのまとめ
そろそろこの辺でコイルとコンデンサが頭の中でゴチャゴチャになっていると思うので、ここまでのことをまとめて整理しておきます。
| 回路素子 | コイル( $\boldsymbol{L}$ ) | コンデンサ( $\boldsymbol{C}$ ) |
|---|---|---|
| リアクタンス | 誘導性リアクタンス | 容量性リアクタンス |
| リアクタンスの記号 (一般的に) |
$X_L$ | $X_C$ |
| リアクタンスの大きさ | $X_L=\dfrac{V}{I}$ | $X_C=\dfrac{V}{I}$ |
| $\boldsymbol{f}$ と $\boldsymbol{L}$(または $\boldsymbol{C}$ )で表わしたリアクタンスの大きさ | $X_L=2\pi fL$ | $X_C=\dfrac{1}{2\pi fC}$ |
| 電流の大きさ | $I=\dfrac{V}{X_L}$ | $I=\dfrac{V}{X_C}$ |
| $\boldsymbol{f}$ と $\boldsymbol{L}$(または $\boldsymbol{C}$ )で表わした電流の大きさ | $I=\dfrac{V}{2\pi fL}$ (周波数が大きくなると電流は小さくなる) |
$I=2\pi fCV$ (周波数が大きくなると電流も大きくなる) |
スポンサーリンク
スポンサーリンク
交流回路の位相 ←BACK
NEXT→ 交流回路のインピーダンス
スポンサーリンク
交流回路のリアクタンス 関連ページ
- 電圧・電流・抵抗
- 第二種電気工事士学科試験の「電気理論」の問題を解くためにおぼえておかなければならない「電圧・電流・抵抗」についてまとめています。「電圧・電流・抵抗」は電気の計算をするために一番初めに理解しておかなくてはならないとても重要な項目なので、しっかりと勉強しておきましょう。
- オームの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「オームの法則」についてまとめています。「オームの法則」は電気の計算をするときの一番基本的な法則になりますので、しっかり勉強しておきましょう。
- 電線の抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「電線の抵抗」についてまとめています。「電線の抵抗」は第二種電気工事士の学科試験でよく出題される重要な項目ですので、しっかり勉強しておきましょう。
- 直列接続と並列接続
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「直列接続と並列接続」についてまとめています。「直列接続と並列接続」は電気回路の基本になる接続方法です。
- 合成抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「合成抵抗」についてまとめています。第二種電気工事士の学科試験では、「合成抵抗」を求める問題がよく出題されています。
- キルヒホッフの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「キルヒホッフの法則」についてまとめています。「キルヒホッフの法則」は電気の計算をするときの重要な法則になりますので、しっかり勉強しておきましょう。
- 直流回路と交流回路
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路と交流回路」についてまとめています。交流回路の最大値と実効値の関係はとても重要で、学科試験でもたまに出題されています。
- 直流回路の計算(基本)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路の計算(基本)」についてまとめています。まずは簡単な直流回路の計算をできるようになりましょう。
- 直流回路の計算(分圧と分流)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「分圧」と「分流」についてまとめています。「分圧」と「分流」は電気回路の計算をするときの考え方の基本になります。
- 電力・電力量・発熱量
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「電力・電力量・発熱量」についてまとめています。電力、電力量、発熱量の違いとそれぞれの求め方をおぼえましょう。
- 正弦波交流波形
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときにおぼえておかなければならない「正弦波交流波形」についてまとめています。「正弦波交流」の最大値または実効値を求める問題は試験でも度々出題されていますので、最大値と実効値の関係式は必ずおぼえておきましょう。
- 交流回路の位相
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路の位相」についてまとめています。「位相」は交流回路の計算をするときにとても重要な考え方です。遅れ位相、進み位相はどのようなものか理解しておきましょう。
- 交流回路のインピーダンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のインピーダンス」についてまとめています。インピーダンスというとちょっとむずかしそうですが、おぼえると簡単です。
- 電気でよく使われる単位
- 第二種電気工事士学科試験の「電気理論」分野で出題される「電気でよく使われる単位」についてまとめています。「単位」は電気を勉強するときの基本中の基本になりますので、しっかりおぼえておきましょう。
- 電気でよく使われるギリシャ文字
- 第二種電気工事士学科試験の計算問題などや単位などで使用されるギリシャ文字の読み方と表わす意味についてまとめています。電気の世界に限らず理系の分野では、色々な量を表わしたり、単位の補助記号としてギリシャ文字が使用されますが、代表的なものだけでもおぼえておくようにしましょう。


