スポンサーリンク
電線の抵抗
※ページ内にPR・広告が含まれる場合があります。
電線は電気を通すためのものですが、電線の抵抗と聞いて、電線に抵抗があるの? と思う方もいると思います。
ですが、電線にも抵抗があります!
たいていの場合、電気回路の計算をするときは電線の抵抗は考えないで計算します。
その理由は、電気回路に使われている「電線以外のものの抵抗(負荷の抵抗)」が「電線の抵抗」と比べるとすごく大きく、電線の抵抗は無視できるくらい小さいからです。
例えば、次のような電池とスイッチと電球がつながれた電気回路があるとします。
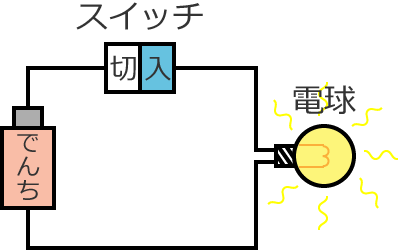
この電気回路の電線と電球の抵抗(負荷の抵抗)を比べると、「電球の抵抗」が「電線の抵抗」の数十倍〜数百倍にもなります。
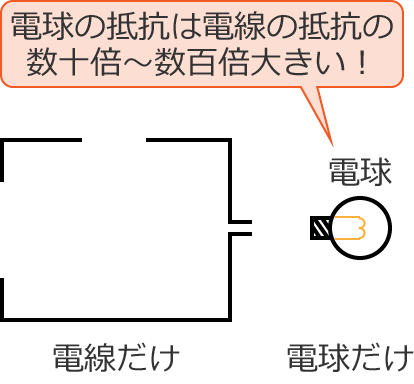
数十倍〜数百倍もある電球の抵抗に対して、すご〜く小さい電線の抵抗は無視して計算しても計算結果にはほとんど影響がないんです。なので、たいていの場合は電線の抵抗を無視して計算します。
が、第二種電気工事士学科試験では、「電線の抵抗を求める問題」が出題されます!
なぜ、電線の抵抗を求める問題が第二種電気工事士の学科試験で出題されるのでしょうか?
みなさんが外を歩いているときに上を見たとします。すると、配電線(電柱から電柱に渡っている電線)が見えます。(配電線については配電線とは?のページで解説します。)
「この配電線ってどこまで続いているんだろう?」って、思う人はいないか…、線路じゃないし…。
いるかいないかは別として、配電線があります。
配電線はすご〜く長いので、配電線の電線の抵抗はある程度の大きさになってしまいます。
そのため、配電線のように電線が長い場合には、電線の抵抗をちゃんと計算しなくてはならない場合があるんです、電気工事士として。なので、第二種電気工事士学科試験で出題されています。
ぉゃっ? 電線が長くなると抵抗が大きくなるの?
電線の抵抗の大きさは、電線の長さや太さで変わります。
つづきは、次の項目で。
スポンサーリンク
電線の抵抗の大きさ
電線の抵抗の大きさは、電線が長くなると大きくなって、短くなると小さくなります。
また、電線が太くなると小さくなって、細くなると大きくなります。
電線の長さが2倍になった場合
次のように長さが $1\,\mathrm{m}$ で、このときの抵抗の大きさが $1\,\Omega$ の電線があるとします。
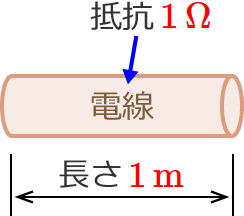
この電線の長さが $2$ 倍になった場合、抵抗は $2$ 倍の $2\,\Omega$ になります。(電線の太さはどちらも同じとします。)
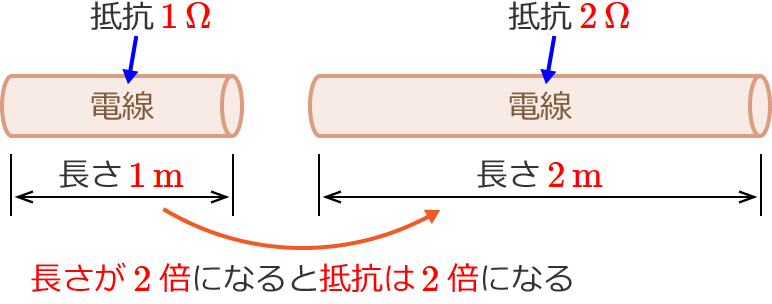
電線の長さが半分(1/2倍)になった場合
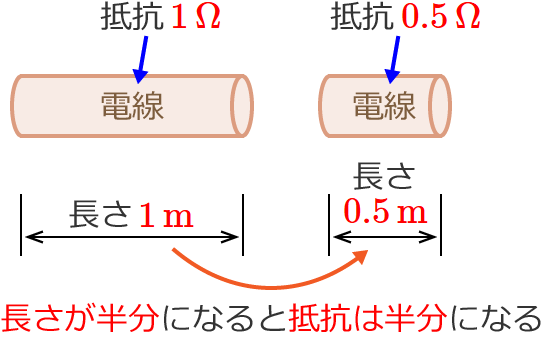
電線の長さが半分 $\left(\dfrac{1}{2}\,\text{倍}\right)$ になった場合、抵抗は半分の $0.5\,\Omega$ になります。(電線の太さはどちらも同じとします。)
電線の太さ(断面積)が2倍になった場合
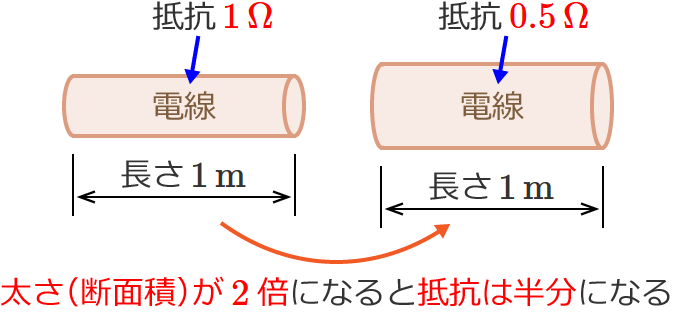
電線の太さ(断面積)が $2$ 倍になった場合、抵抗は半分の $0.5\,\Omega$ になります。(電線の長さはどちらも同じとします。)
電線の太さ(断面積)が半分(1/2倍)になった場合
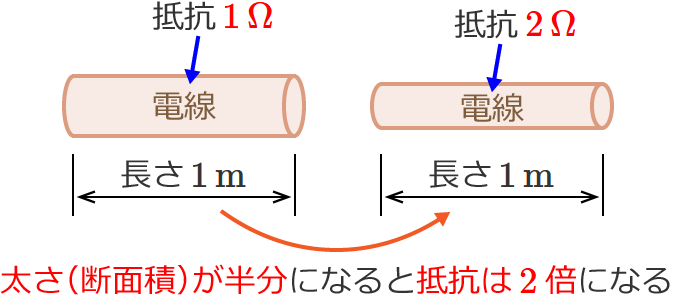
電線の太さ(断面積)が半分 $\left(\dfrac{1}{2}\,\text{倍}\right)$ になった場合、抵抗は $2$ 倍の $2\,\Omega$ になります。(電線の長さはどちらも同じとします。)
電線の太さ(直径)が2倍になった場合
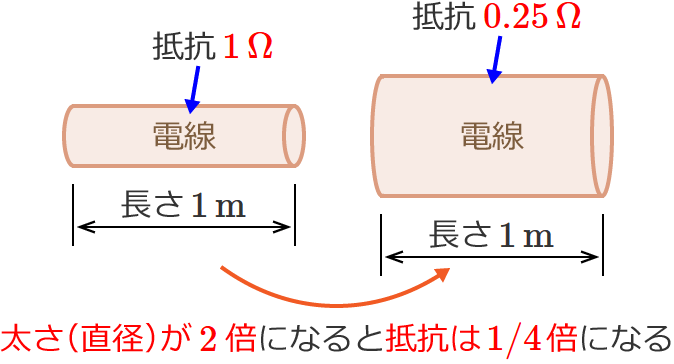
電線の太さ(直径)が $2$ 倍になった場合、抵抗は $\dfrac{1}{4}$ 倍 $\left( =\dfrac{1}{2^2}\,\text{倍}\right)$ の $0.25\,\Omega$ になります。(電線の長さはどちらも同じとします。)
電線の太さ(直径)が半分(1/2倍)になった場合
電線の太さ(直径)が半分 $\left(\dfrac{1}{2}\,\text{倍}\right)$ になった場合、抵抗は $4$ 倍 $\left( =2^2\,\text{倍}\right)$ の $4\,\Omega$ になります。(電線の長さはどちらも同じとします。)
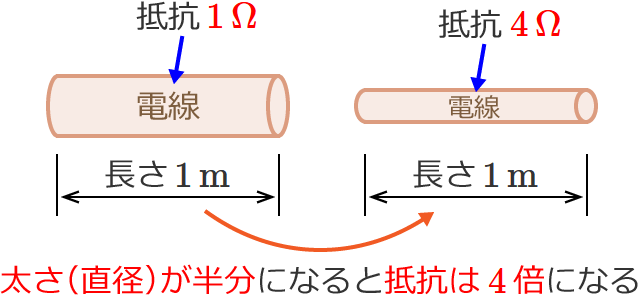
どうでしょう、「電線の長さ・太さ」と「抵抗の大きさ」の関係のイメージはつかめたでしょうか?
電線の抵抗は、電線が長くなると大きくなって、電線が太くなると小さくなる。
つまり、
- 電線の抵抗を小さくするためには、電線を短く、太くする
- 電線の抵抗を大きくするためには、電線を長く、細くする
ということになります。
電線の抵抗は小さい方がいいので、電線は短く、太くするのが理想的ですが、現実的には電線の長さは必要な分の長さが必要で、あまり太くすると重くなるので、適当な長さ、太さにする必要があります。
また、電線の材料には銅やアルミがよく使用されますが、電線を太くすると電線に使用する材料(銅やアルミ)が多くなり、電線の単価が上がってしまい不経済になります。
スポンサーリンク
スポンサーリンク
電線の抵抗の公式(その前に抵抗率とは?)
前の項目(電線の抵抗の大きさ)で、「電線の長さ・太さ」と「抵抗の大きさ」との関係がイメージできたと思います。
では次に、電線の抵抗の大きさを求めるために必要な抵抗率について解説します。
抵抗率とは、電線に使用される材料によって決まっている値で、抵抗率が小さい材料を電線に使用すると電線の抵抗は小さくなり、抵抗率が大きい材料を電線に使用すると電線の抵抗は大きくなります。
代表的な金属の抵抗率は、次のようになります。
| 材料 | 抵抗率[$\Omega\,\cdotp\mathrm{m}$] |
|---|---|
| 銀 | $1.62\times 10^{-8}$(抵抗率が小さい) |
| 軟銅 | $1.72\times 10^{-8}$( ↓ ) |
| 金 | $2.40\times 10^{-8}$( ↓ ) |
| アルミニウム | $2.82\times 10^{-8}$( ↓ ) |
| 鉄 | $10.0\times 10^{-8}$(抵抗率が大きい) |
この中では銀の抵抗率が一番小さいので、電線に銀を使用すると電線の抵抗を小さくすることができるのですが、銀は高い!ので、一般的には銅またはアルミニウムが使用されています。(銅もアルミニウムもそこそこ高いけどね。)
抵抗率の単位は「$\Omega\,\cdotp\mathrm{m}$」と書いて、「オームメートル」と読みます。また、抵抗率を表わす記号には一般的にギリシャ文字の「$\rho$」を使います。「$\rho$」は「ロー」と読みます。
第二種電気工事士学科試験では上表の抵抗率の値そのものについて問われる問題は出題されませんが(たぶん)、抵抗率の大きい順(または小さい順)はおぼえておきましょう。
電線の抵抗の公式
ここまでで「電線の長さ・太さと抵抗の大きさのイメージ」、「抵抗率」について分かったと思うので、次は、電線の抵抗の大きさを求めるための公式について解説します。
第二種電気工事士学科試験の問題を解くために使う電線の抵抗の公式には2つあるので、両方おぼえておきましょう。
抵抗の公式(その1)
1つ目は電線の太さが断面積の場合の公式で、次式で表わされます。
$R=\rho\dfrac{L}{S}$ [$\Omega$]
この式の中で使われている記号はそれぞれ、
$R$ :抵抗 [$\Omega$]
$\rho$ :抵抗率 [$\Omega\,\cdotp\mathrm{m}$]
$L$ :電線の長さ [$\mathrm{m}$]
$S$ :電線の断面積(太さ)[$\mathrm{m^2}$]
です。
イメージしやすいように図で書いてみると、次のようになります。
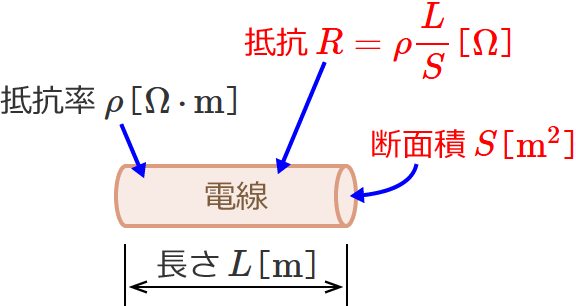
公式をみると分かるように、電線の抵抗 $R$ は、抵抗率 $\rho$ が分かっている場合、電線の長さ $L$ と断面積 $S$ が分かれば求められます。
また、
- 電線の長さ $\boldsymbol{L}$ が $\boldsymbol{2}$ 倍になると、抵抗の大きさ $\boldsymbol{R}$ も $\boldsymbol{2}$ 倍
- 電線の断面積 $\boldsymbol{S}$ が $\boldsymbol{2}$ 倍になると、抵抗の大きさ $\boldsymbol{R}$ は半分 $\boldsymbol{\left(\dfrac{1}{2}\,\text{倍}\right)}$
になることも、公式から分かります。
抵抗の公式(その2)
2つ目は電線の太さが直径の場合の公式で、次式で表わされます。
$R=\dfrac{4\rho L}{\pi D^2}$ [$\Omega$]
この式の中で使われている記号はそれぞれ、
$R$ :抵抗 [$\Omega$]
$\rho$ :抵抗率 [$\Omega\,\cdotp\mathrm{m}$]
$L$ :電線の長さ [$\mathrm{m}$]
$D$ :電線の直径(太さ)[$\mathrm{m}$]
です。ちなみに、公式中の $\pi$ は円周率の $\pi$($=3.14159265\ldots$)です。
図で書いてみると、次のようになります。
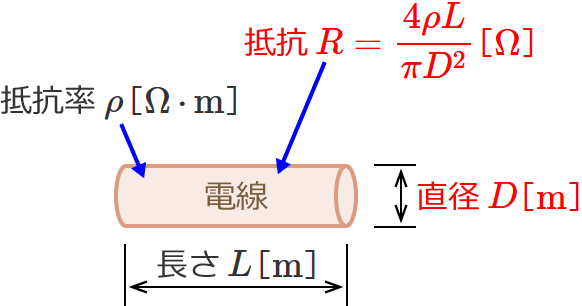
公式をみると分かるように、電線の抵抗 $R$ は、抵抗率 $\rho$ が分かっている場合、電線の長さ $L$ と直径 $D$ が分かれば求められます。
また、
- 電線の長さ $\boldsymbol{L}$ が $\boldsymbol{2}$ 倍になると、抵抗の大きさ $\boldsymbol{R}$ も $\boldsymbol{2}$ 倍
- 電線の直径 $\boldsymbol{D}$ が $\boldsymbol{2}$ 倍になると、抵抗の大きさ $\boldsymbol{R}$ は $\boldsymbol{\dfrac{1}{2^2}=\dfrac{1}{4}}$ 倍
になることも、公式から分かります。
抵抗の公式(その1)から抵抗の公式(その2)の導出
円の面積の公式を使うと、抵抗の公式(その1)から抵抗の公式(その2)を導くことができます。円の面積 $S$ は、円の直径を $D$ とすると、
$S=\pi\times\left(\dfrac{D}{2}\right)^2$ と表わされます。($D$ は円の直径なので、$2$ で割ると半径です。)
この $S$ を抵抗の公式(その1)に代入すると、
$R=\rho\dfrac{L}{S} =\rho\times\dfrac{L}{\pi\times\left(\dfrac{D}{2}\right)^2}$ $=\rho\times\dfrac{L}{\dfrac{\pi D^2}{4}}$ $=\rho\times\dfrac{4L}{\pi D^2}$ $=\dfrac{4\rho L}{\pi D^2}$
$\therefore R=\dfrac{4\rho L}{\pi D^2}$
となり、抵抗の公式(その2)の式になります。式の導出の方法をおぼえておくと、おぼえる式は1つだけ(抵抗の公式(その1)だけ)ですむので、導出方法もおぼえておくといいと思います。
第二種電気工事士学科試験では、抵抗に関する問題がよく出題されています。
出題される問題は、このページの2つの抵抗の公式をおぼえておけば解ける問題がほとんどなので、抵抗の公式は両方ともおぼえておきましょう。
また、第二種電気工事士学科試験では、電線の断面積の単位は[$\mathrm{mm^2}$]、電線の直径の単位は[$\mathrm{mm}$]で与えられることが多いので、抵抗の問題を解くときは単位に注意しましょう!
断面積と直径の単位の換算
このページの抵抗の公式の電線の断面積の単位は[$\mathrm{m^2}$]、電線の直径の単位は[$\mathrm{m}$]です。
なので、試験問題で電線の断面積の単位が[$\mathrm{mm^2}$]で与えられた場合には、単位を[$\mathrm{m^2}$]に直して(換算して)抵抗の公式に代入します。[$\mathrm{mm^2}$]を[$\mathrm{m^2}$]に直すときは、$10^{-6}$ をかけます。
例)$5.5$[$\mathrm{mm^2}$] $\Rightarrow$ $10^{-6}$ をかける $\Rightarrow$ $5.5\times 10^{-6}$[$\mathrm{m^2}$]
また、電線の直径の単位が[$\mathrm{mm}$]で与えられた場合には、単位を[$\mathrm{m}$]に直して(換算して)抵抗の公式に代入します。[$\mathrm{mm}$]を[$\mathrm{m}$]に直すときは、$10^{-3}$ をかけます。
例)$1.6$[$\mathrm{mm}$] $\Rightarrow$ $10^{-3}$ をかける $\Rightarrow$ $1.6\times 10^{-3}$[$\mathrm{m}$]
スポンサーリンク
スポンサーリンク
スポンサーリンク
電線の抵抗 関連ページ
- 電圧・電流・抵抗
- 第二種電気工事士学科試験の「電気理論」の問題を解くためにおぼえておかなければならない「電圧・電流・抵抗」についてまとめています。「電圧・電流・抵抗」は電気の計算をするために一番初めに理解しておかなくてはならないとても重要な項目なので、しっかりと勉強しておきましょう。
- オームの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「オームの法則」についてまとめています。「オームの法則」は電気の計算をするときの一番基本的な法則になりますので、しっかり勉強しておきましょう。
- 直列接続と並列接続
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「直列接続と並列接続」についてまとめています。「直列接続と並列接続」は電気回路の基本になる接続方法です。
- 合成抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「合成抵抗」についてまとめています。第二種電気工事士の学科試験では、「合成抵抗」を求める問題がよく出題されています。
- キルヒホッフの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「キルヒホッフの法則」についてまとめています。「キルヒホッフの法則」は電気の計算をするときの重要な法則になりますので、しっかり勉強しておきましょう。
- 直流回路と交流回路
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路と交流回路」についてまとめています。交流回路の最大値と実効値の関係はとても重要で、学科試験でもたまに出題されています。
- 直流回路の計算(基本)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路の計算(基本)」についてまとめています。まずは簡単な直流回路の計算をできるようになりましょう。
- 直流回路の計算(分圧と分流)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「分圧」と「分流」についてまとめています。「分圧」と「分流」は電気回路の計算をするときの考え方の基本になります。
- 電力・電力量・発熱量
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「電力・電力量・発熱量」についてまとめています。電力、電力量、発熱量の違いとそれぞれの求め方をおぼえましょう。
- 正弦波交流波形
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときにおぼえておかなければならない「正弦波交流波形」についてまとめています。「正弦波交流」の最大値または実効値を求める問題は試験でも度々出題されていますので、最大値と実効値の関係式は必ずおぼえておきましょう。
- 交流回路の位相
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路の位相」についてまとめています。「位相」は交流回路の計算をするときにとても重要な考え方です。遅れ位相、進み位相はどのようなものか理解しておきましょう。
- 交流回路のリアクタンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のリアクタンス」についてまとめています。コイルのリアクタンス(誘導性リアクタンス)とコンデンサのリアクタンス(容量性リアクタンス)の違いをおぼえておきましょう。
- 交流回路のインピーダンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のインピーダンス」についてまとめています。インピーダンスというとちょっとむずかしそうですが、おぼえると簡単です。
- 電気でよく使われる単位
- 第二種電気工事士学科試験の「電気理論」分野で出題される「電気でよく使われる単位」についてまとめています。「単位」は電気を勉強するときの基本中の基本になりますので、しっかりおぼえておきましょう。
- 電気でよく使われるギリシャ文字
- 第二種電気工事士学科試験の計算問題などや単位などで使用されるギリシャ文字の読み方と表わす意味についてまとめています。電気の世界に限らず理系の分野では、色々な量を表わしたり、単位の補助記号としてギリシャ文字が使用されますが、代表的なものだけでもおぼえておくようにしましょう。


