スポンサーリンク
正弦波交流波形
※ページ内にPR・広告が含まれる場合があります。
このページでは、正弦波交流波形について解説します。
正弦波交流の波形、最大値と実効値、周波数と周期などについて解説していますので、正弦波交流とはどういうもので、正弦波交流の最大値、実効値、周波数、周期とは何か? などについて勉強してみましょう。
正弦波交流って、ふだんの生活の中ではあまり聞かない言葉だと思うんですが、実はすぐ身近なところで見つけることができるんですよね、正弦波交流。
例えば、みなさんのおうちにある「コ…」「コンセ…」(あー、まだ言えない。続きを読んでみよう!)
スポンサーリンク
正弦波交流電圧の最大値と実効値
正弦波交流の最大値と実効値については直流回路と交流回路のページでも解説しましたが、大事なことなのでこのページでももう一度さらっと復習して、解説を追加します。
まず、正弦波交流電圧は次のような波形でした。
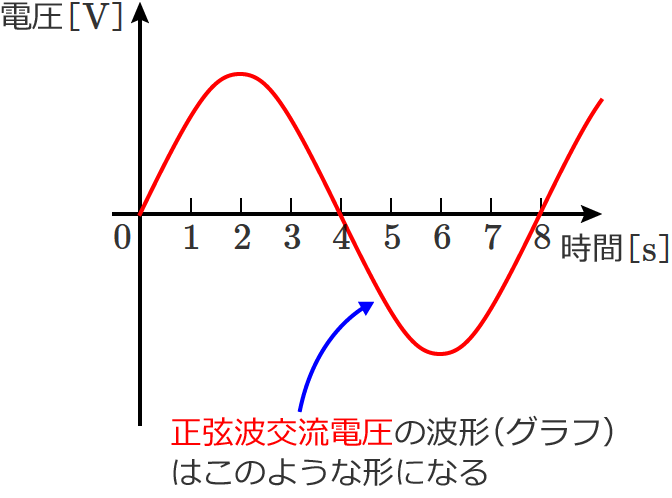
それから、正弦波交流電圧は、
- 交流なので、時間の経過とともに電圧がプラスになったりマイナスになったりする
- 波形の頂点の値が最大値になる
- 最大値を $\boldsymbol{\sqrt{2}}$ で割った値が実効値になる
ということでした。
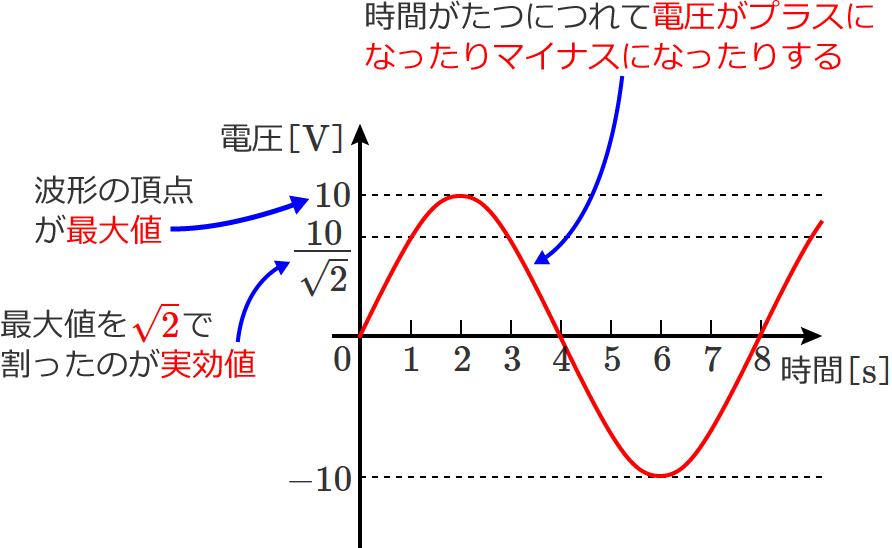
ところで、正弦波交流電圧を発生する電源はどこにあって、何に使われているでしょうか?
これは、周りを見渡すとすぐに見つけることができます。
はい、ありました。答えは、コンセントにあって、電化製品などに使われています!です。

では次に、コンセントから出力される正弦波交流電圧の波形(どんなグラフになるか?)について考えてみましょう。
「コンセントの電圧は何ボルト?」と聞かれると、ほとんどの方は「 $100$ ボルト!」と答えると思いますが、ではまた質問で、この $100$ ボルトは、最大値? 実効値? どちらのことを言っているでしょうか?
この $100$ ボルトは実効値のことを言っています。
ふつう、交流で「$100$ ボルト!」とか「$200$ ボルト!」と言えば、それは実効値のことを言っていて、実効値が $100\,\mathrm{V}$ の交流電圧は、直流の $100\,\mathrm{V}$ と同等の働きをする大きさの電圧になります。
では、コンセントの電圧 $100\,\mathrm{V}$ は実効値なので、正弦波交流の最大値と実効値の関係式(最大値 $=\sqrt{2} \ \times$ 実効値)よりコンセントの電圧の最大値を求めてみましょう。(正弦波交流の最大値を求めるときは、実効値に $\sqrt{2}$ をかけるのでした。)
コンセントの電圧の最大値は、
最大値 $=\sqrt{2} \ \times$ 実効値 $=\sqrt{2}\times100$ $\fallingdotseq 1.41\times 100=141$ [$\mathrm{V}$]
$\therefore$ コンセントの電圧の最大値 $=141$ [$\mathrm{V}$]
となります。なので、コンセントには、最大で約 $141\,\mathrm{V}$ の電圧がきているんですね。Max $100\,\mathrm{V}$ じゃないんですね。
以上ここまでで、コンセントの電圧について次のことが分かりました。
- コンセントの電圧は正弦波交流電圧
- コンセントの電圧の実効値は $\boldsymbol{100\,\mathrm{V}}$
- コンセントの電圧の最大値は $\boldsymbol{141\,\mathrm{V}}$
ここまで分かると、コンセントの電圧波形は次のようになるんじゃないかな? と予想できると思います。
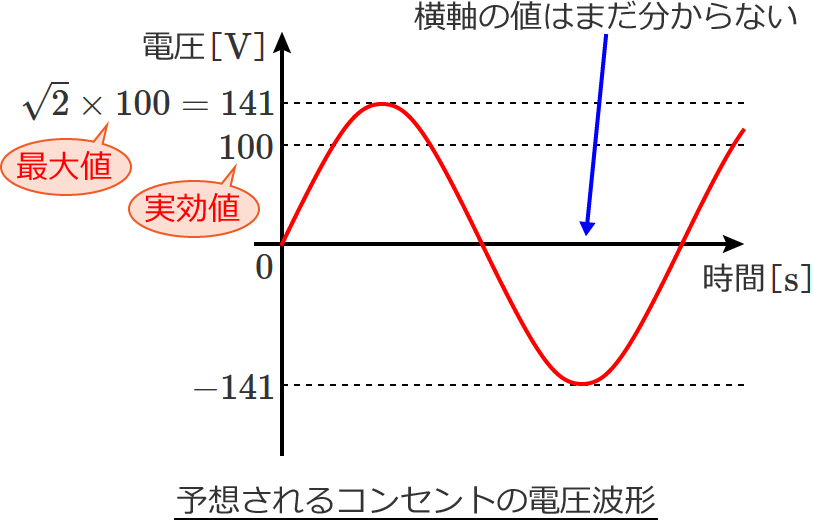
横軸(時間)の値については、まだ分かりませんよ。横軸の値については、次の項目(正弦波交流電圧波形の周波数と周期)で解説します。
それから、正弦波交流電圧の最大値と実効値の関係( $\sqrt{2}$ をかけるか、$\sqrt{2}$ で割るか)についての問題は、第二種電気工事士学科試験でも出題されているので、必ずおぼえておくようにしましょう。
スポンサーリンク
スポンサーリンク
正弦波交流電圧波形の周波数と周期
波形(グラフの形)について考えるとき、周波数と周期というのがあります。
この周波数と周期は、波形の横軸(時間軸)の値を与えるもので、交流波形を考えるときに大事な値になります。
それでは、周波数、周期、それから周波数と周期の関係について順番に解説していきます。
正弦波交流電圧波形の周波数
周波数とは、$\boldsymbol{1}$ 秒間に波が何回繰り返されるか?を表わす値で、周波数の単位は「 $\mathrm{Hz}$ 」と書いて「ヘルツ」と読みます。
「ヘルツ」って聞いたことありますよね?
例えば、携帯、スマホ、無線などの電波の周波数、コンセントの電源の周波数、パソコンのCPUのクロック数(CPUの性能を表わす数値)などの単位に使われています。
「あなたのおうちのコンセントは何ヘルツ?」
「私んちは $50$ ヘルツ!」
みたいな…。
周波数とは「 $1$ 秒間に波が何回繰り返されるか?」というものですが、これを波形で考えてみると次のようになります。
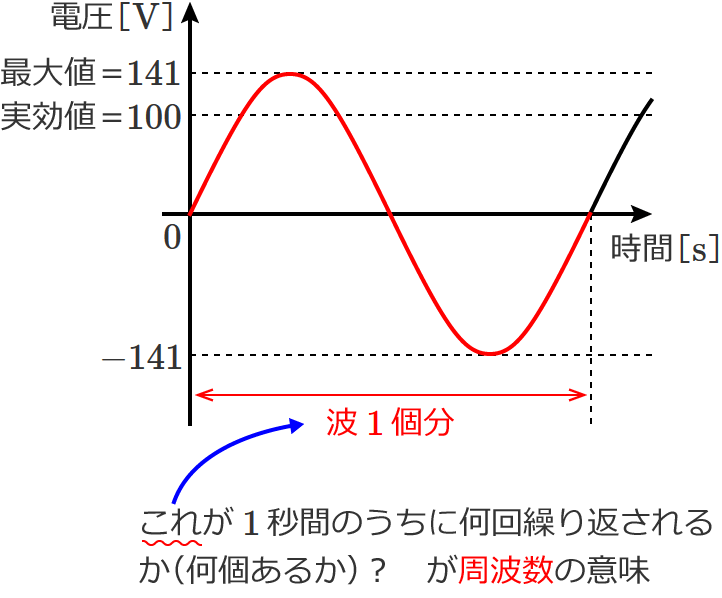
なので、コンセントの電圧の周波数が $50\,\mathrm{Hz}$ の場合は、次のように波が $1$ 秒間に $50$ 回繰り返されていることになります。
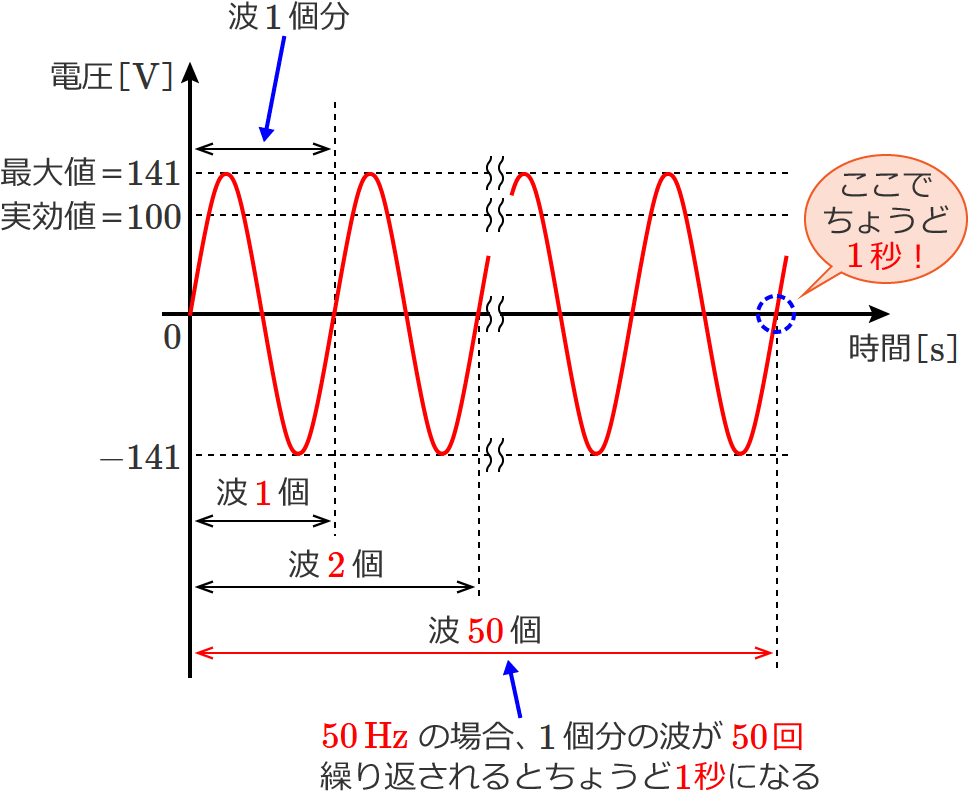
ちなみに、コンセントの電圧の周波数は、関東から北の地域(東日本)では $50\,\mathrm{Hz}$、関東より南(西?)の地域(西日本)では $60\,\mathrm{Hz}$ になります。
$60\,\mathrm{Hz}$ の場合は、$1$ 秒間に波 $1$ 個分が $60$ 回繰り返されているということになります。
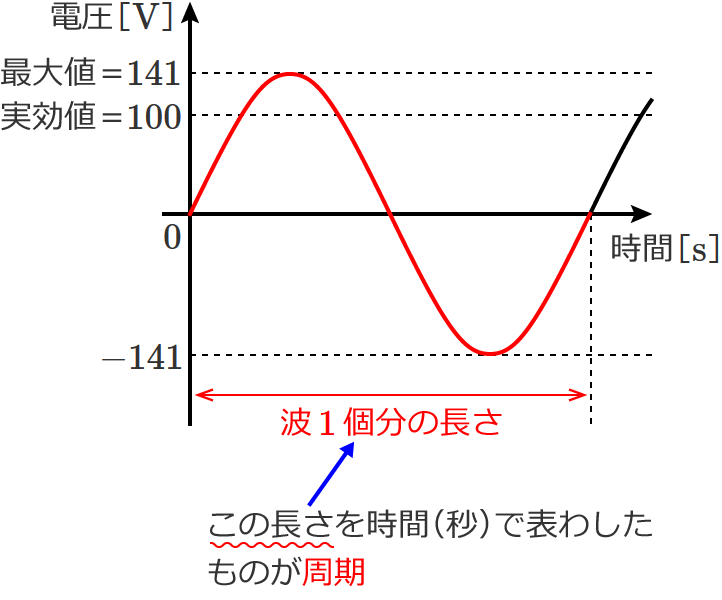
正弦波交流電圧波形の周期
周期とは、波 $\boldsymbol{1}$ 個分の長さを時間で表わしたもので、単位は時間なので「 $\mathrm{s}$ 」(秒)です。波形で考えてみると次のようになります。
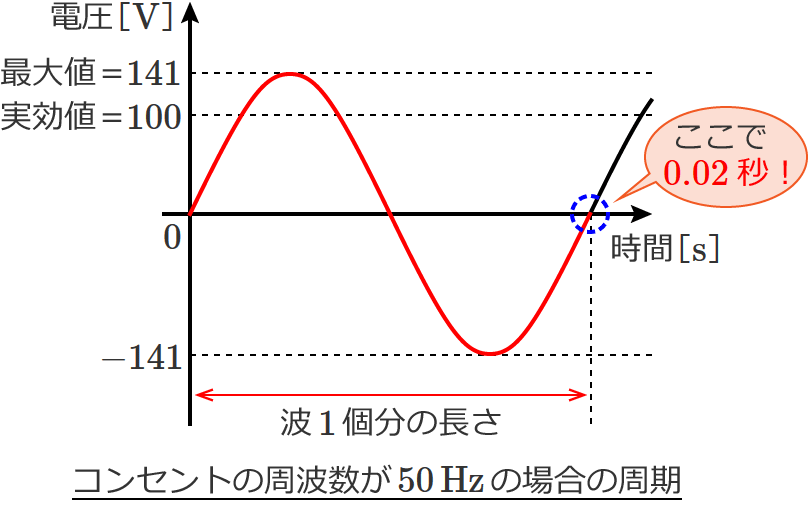
では、コンセントの周波数が $50\,\mathrm{Hz}$ の場合、周期(波 $\boldsymbol{1}$ 個分の長さ)はどのくらいになるでしょうか?
先ほど説明したように、$50\,\mathrm{Hz}$ の場合は、「 $1$ 個分の波が $50$ 回繰り返されると $1$ 秒になる」のでした。つまり、「 $1$ 秒間の中に波が $50$ 個入っている」ということなので、$\boldsymbol{1}$ 秒を $\boldsymbol{50}$ 分割すれば周期(波 $\boldsymbol{1}$ 個分の長さ)になります。したがって、
$\therefore 50\,\mathrm{Hz}$ の周期 $=\dfrac{1\text{[}\mathrm{s}\text{]}}{50\text{[}\mathrm{Hz}\text{]}} =0.02$ [$\mathrm{s}$]
となります。
けっこう短い時間ですよね!
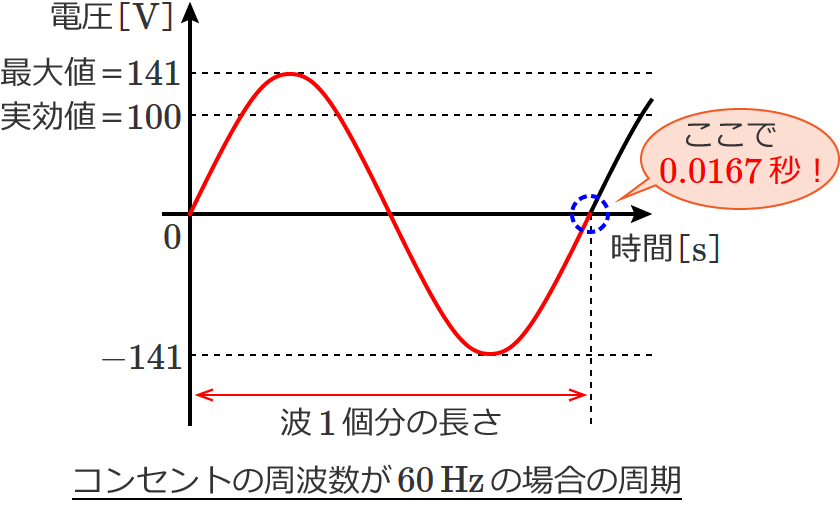
$60\,\mathrm{Hz}$ のときはもっと短いですよ!
$\therefore 60\,\mathrm{Hz}$ の周期 $=\dfrac{1\text{[}\mathrm{s}\text{]}}{60\text{[}\mathrm{Hz}\text{]}}\fallingdotseq 0.0167$ [$\mathrm{s}$]
正弦波交流電圧波形の周波数と周期の関係
ここまでの説明でだいたい予想がつくと思いますが、周波数を $f$[$\mathrm{Hz}$]、周期を $T$[$\mathrm{s}$]とすると、周波数と周期には次の関係があります。
$\therefore f=\dfrac{1}{T}$ [$\mathrm{Hz}$]
$\therefore T=\dfrac{1}{f}$ [$\mathrm{s}$]
周波数と周期は、お互いに逆数の関係になります。
スポンサーリンク
スポンサーリンク
電力・電力量・発熱量 ←BACK
NEXT→ 交流回路の位相
スポンサーリンク
正弦波交流波形 関連ページ
- 電圧・電流・抵抗
- 第二種電気工事士学科試験の「電気理論」の問題を解くためにおぼえておかなければならない「電圧・電流・抵抗」についてまとめています。「電圧・電流・抵抗」は電気の計算をするために一番初めに理解しておかなくてはならないとても重要な項目なので、しっかりと勉強しておきましょう。
- オームの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「オームの法則」についてまとめています。「オームの法則」は電気の計算をするときの一番基本的な法則になりますので、しっかり勉強しておきましょう。
- 電線の抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「電線の抵抗」についてまとめています。「電線の抵抗」は第二種電気工事士の学科試験でよく出題される重要な項目ですので、しっかり勉強しておきましょう。
- 直列接続と並列接続
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「直列接続と並列接続」についてまとめています。「直列接続と並列接続」は電気回路の基本になる接続方法です。
- 合成抵抗
- 第二種電気工事士学科試験の「電気理論」の分野で出題される「合成抵抗」についてまとめています。第二種電気工事士の学科試験では、「合成抵抗」を求める問題がよく出題されています。
- キルヒホッフの法則
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くときに使う「キルヒホッフの法則」についてまとめています。「キルヒホッフの法則」は電気の計算をするときの重要な法則になりますので、しっかり勉強しておきましょう。
- 直流回路と交流回路
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路と交流回路」についてまとめています。交流回路の最大値と実効値の関係はとても重要で、学科試験でもたまに出題されています。
- 直流回路の計算(基本)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「直流回路の計算(基本)」についてまとめています。まずは簡単な直流回路の計算をできるようになりましょう。
- 直流回路の計算(分圧と分流)
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなけらばならない「分圧」と「分流」についてまとめています。「分圧」と「分流」は電気回路の計算をするときの考え方の基本になります。
- 電力・電力量・発熱量
- 第二種電気工事士学科試験の「電気理論」の計算問題を解くためにおぼえておかなければならない「電力・電力量・発熱量」についてまとめています。電力、電力量、発熱量の違いとそれぞれの求め方をおぼえましょう。
- 交流回路の位相
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路の位相」についてまとめています。「位相」は交流回路の計算をするときにとても重要な考え方です。遅れ位相、進み位相はどのようなものか理解しておきましょう。
- 交流回路のリアクタンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のリアクタンス」についてまとめています。コイルのリアクタンス(誘導性リアクタンス)とコンデンサのリアクタンス(容量性リアクタンス)の違いをおぼえておきましょう。
- 交流回路のインピーダンス
- 第二種電気工事士学科試験の「電気理論」の問題を解くときにおぼえておかなければならない「交流回路のインピーダンス」についてまとめています。インピーダンスというとちょっとむずかしそうですが、おぼえると簡単です。
- 電気でよく使われる単位
- 第二種電気工事士学科試験の「電気理論」分野で出題される「電気でよく使われる単位」についてまとめています。「単位」は電気を勉強するときの基本中の基本になりますので、しっかりおぼえておきましょう。
- 電気でよく使われるギリシャ文字
- 第二種電気工事士学科試験の計算問題などや単位などで使用されるギリシャ文字の読み方と表わす意味についてまとめています。電気の世界に限らず理系の分野では、色々な量を表わしたり、単位の補助記号としてギリシャ文字が使用されますが、代表的なものだけでもおぼえておくようにしましょう。


