電気数学のお勉強｜三角関数｜三角関数のsin、cos、tanって何？

スポンサーリンク

数学に三角関数ってありますよね？

 

高校の数学で習ったと思うんですが、中学校でしたっけ？　高校ですよね？　ま、いっか。

 

三角関数ってあれですよ、

• $\boldsymbol{\sin}$
• $\boldsymbol{\cos}$
• $\boldsymbol{\tan}$

とかで、$\sin$（サイン）、$\cos$（コサイン）、$\tan$（タンジェント）が入っている式を見ただけで、「うわ〜、苦手〜。」って思ってしまう方も多かったりするんですが、三角関数、特にその基本になる $\sin \theta$ 、$\cos \theta$ 、$\tan \theta$ の基本的なところはそれほど難しくなく、使ってみると「そんなもんか…」と意外に簡単だったりします。（「$\theta$」ってシータです。）

 

まずは何事も基本からということで、このページでは三角関数の $\sin \theta$ 、$\cos \theta$ 、$\tan \theta$ の基本について解説します。

 

スポンサーリンク

 

三角関数のsin（サイン）

三角関数の $\sin$ 、$\cos$ 、$\tan$ を考えるときは、直角三角形で考えます。

 

直角三角形ですよ！　直角！

 

なので、次のような三角形で考えてはダメです。

 

 

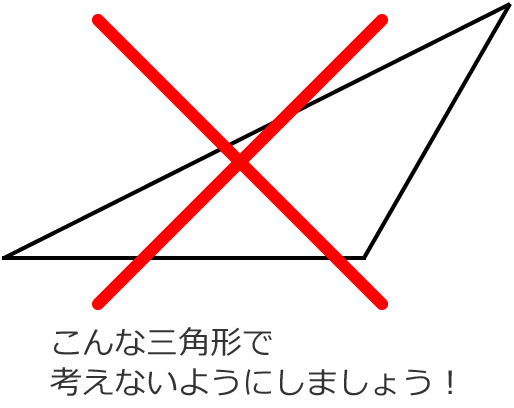
直角三角形は次のように一つの角が直角になっている三角形ですね。

 

 

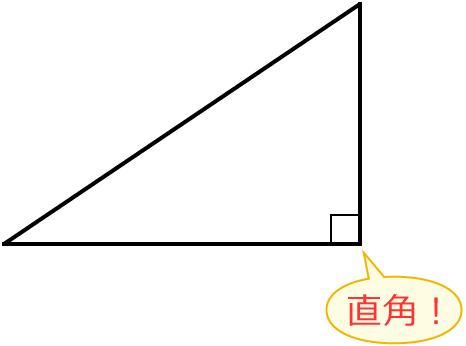
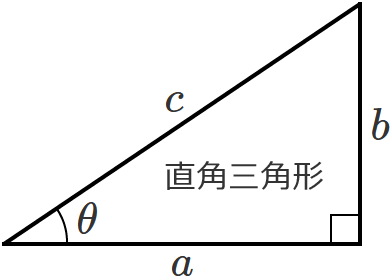
では、この直角三角形に辺の長さ（ $a$ 、$b$ 、$c$ ）と角度（ $\theta$ ）を書き入れてみます。

 

 

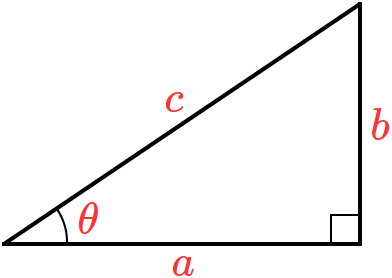
ここで、この場合の角度 $\theta$ は、図の三角形の左側としていることに注意しましょう。三角形の上側を角度 $\theta$ とすると、この後の話も変わってきますので…。てか、$\theta$ をどこにするかで $\sin \theta$ 、$\cos \theta$ 、$\tan \theta$ が変わります。

 

それで上の図のように辺の長さを $a$ 、$b$ 、$c$ 、角度を $\theta$ とすると、直角三角形の $\sin \theta$ は、

 

$\sin \theta = \dfrac{b}{c}$　…①　となります。

 

つまり、直角三角形が上の図のようなときに、辺の長さ $b$ を $c$ で割った $\left( \dfrac{b}{c} \right)$ のが $\sin \theta$ の値ですよ、ということですね。

 

 

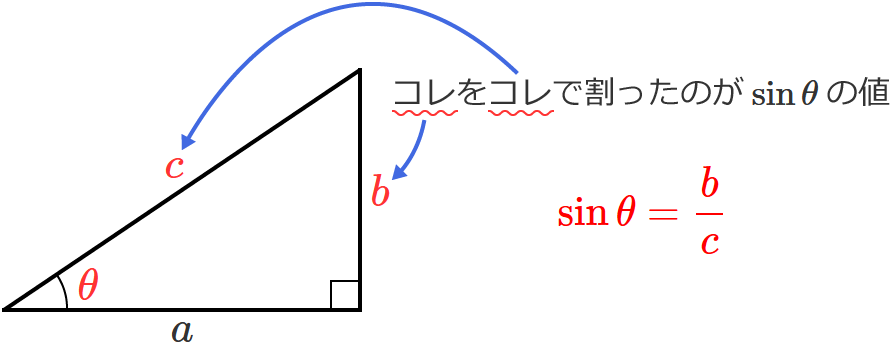
それから、$\sin \theta$ が使われるパターン（計算）で多いのは、こんなのですね。

 

次のように直角三角形の辺 $c$ の長さと角度 $\theta$だけが分かっているとします。このとき、辺 $b$ の長さはいくら？

 

 

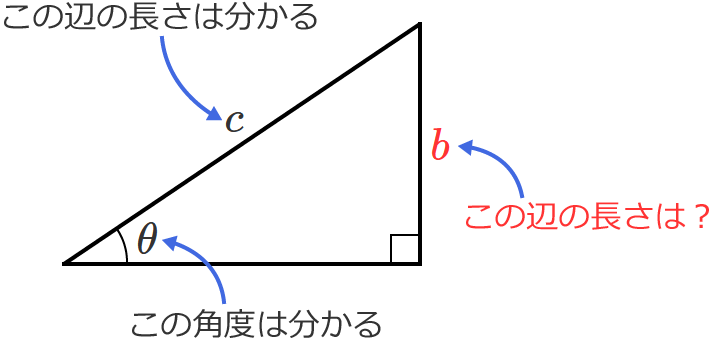
これは、先ほどの①式から簡単に分かります。

 

①式は、$\sin \theta = \dfrac{b}{c}$ でした。

 

これを変形すると、$b = c \times \sin \theta$ となり、辺の長さ $c$ と角度 $\theta$ が分かれば辺の長さ $b$ を求めることができます。これはよく使われるのでおぼえておくようにしましょう。（ $\sin \theta$ の値は角度（ $\theta$ ）によって値が決まります。）

 

次は $\cos$（コサイン）です。

 

三角関数のcos（コサイン）

$\cos$ も $\sin$ と同じように直角三角形で考えるので、先ほどと同じ直角三角形を書きます。

 

 

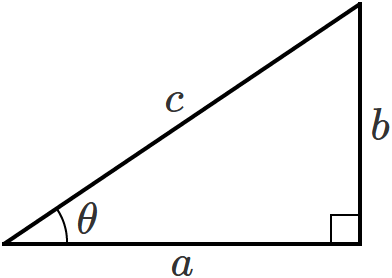
この直角三角形の $\cos \theta$ は、

 

$\cos \theta = \dfrac{a}{c}$　…②　となります。

 

つまり、直角三角形が上の図のようなときに、辺の長さ $a$ を $c$ で割った $\left( \dfrac{a}{c} \right)$ のが $\cos \theta$ の値ですよ、ということですね。

 

 

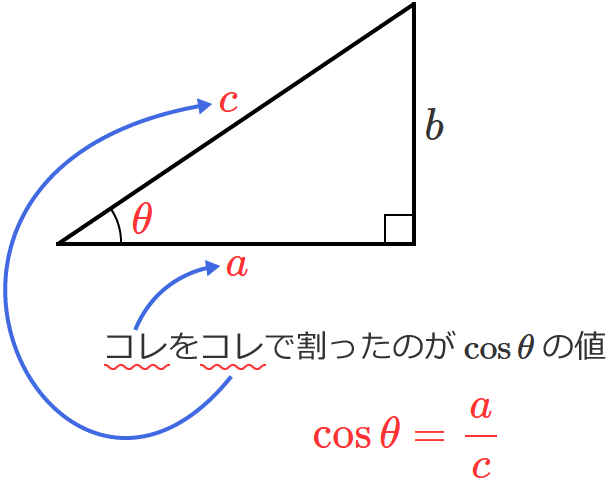
それから、$\cos \theta$ が使われるパターン（計算）で多いのは、$\sin \theta$ と同じようにこんなのですね。

 

次のように直角三角形の辺 $c$ の長さと角度 $\theta$だけが分かっているとします。このとき、辺 $a$ の長さはいくら？

 

 

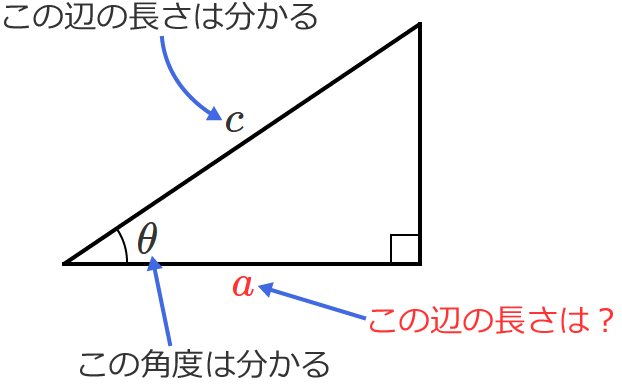
これは、先ほどの②式から簡単に分かります。

 

②式は、$\cos \theta = \dfrac{a}{c}$ でした。

 

これを変形すると、$a = c \times \cos \theta$ となり、辺の長さ $c$ と角度 $\theta$ が分かれば辺の長さ $a$ を求めることができます。（ $\cos \theta$ の値は角度（ $\theta$ ）によって値が決まります。）

 

これもよく使われ、例えばベクトルの成分の大きさ（ベクトルを分解したときの大きさ）を求めるときなどに使われます。

 

 

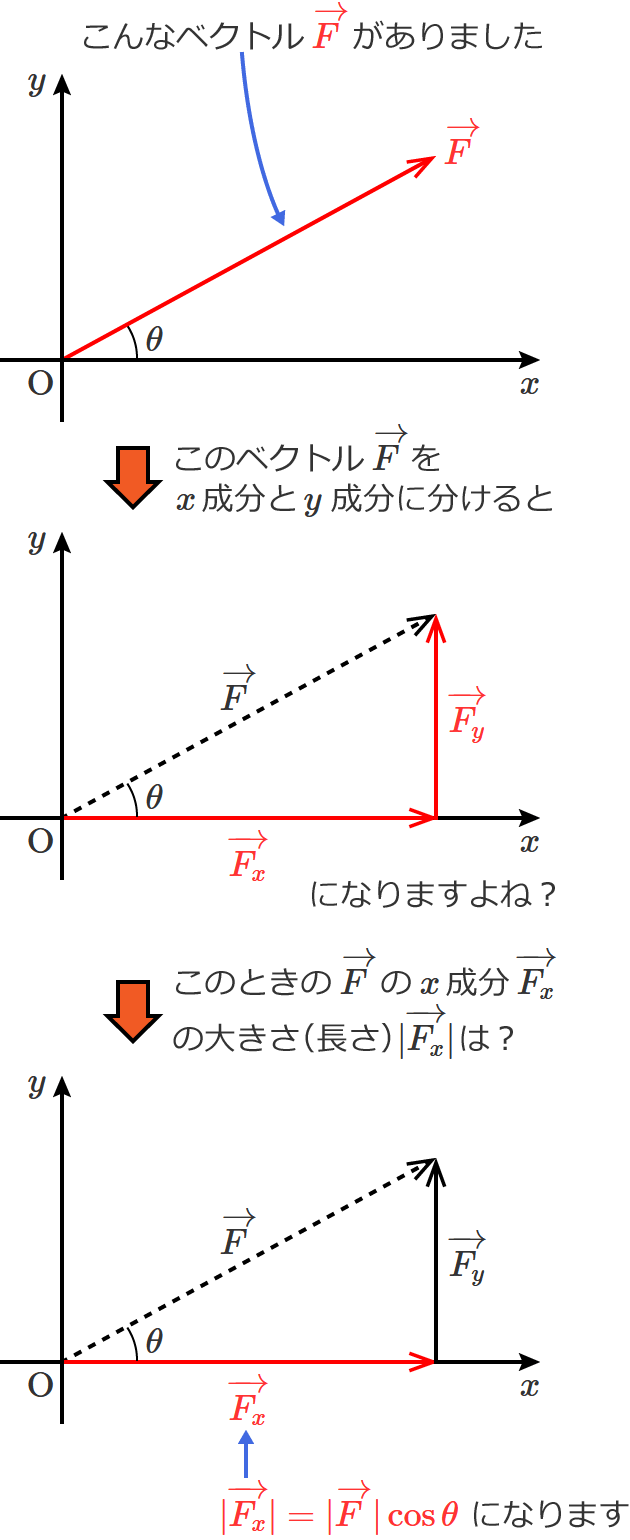
こんな感じのですね。

 

ちなみに、$y$ 成分は $\sin \theta$ を使って、$| \overrightarrow{F_y} | = | \overrightarrow{F} | \sin \theta$ ですよ。

 

最後は $\tan$ （タンジェント）です。

 

三角関数のtan（タンジェント）

またまた同じ直角三角形で考えます。

 

 

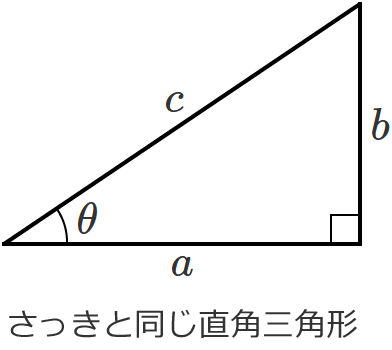
この直角三角形の $\tan \theta$ は、

 

$\tan \theta = \dfrac{b}{a}$　…③　となります。

 

つまり、直角三角形が上の図のようなときに、辺の長さ $b$ を $a$ で割った $\left( \dfrac{b}{a} \right)$ のが $\tan \theta$ の値ですよ、ということですね。

 

 

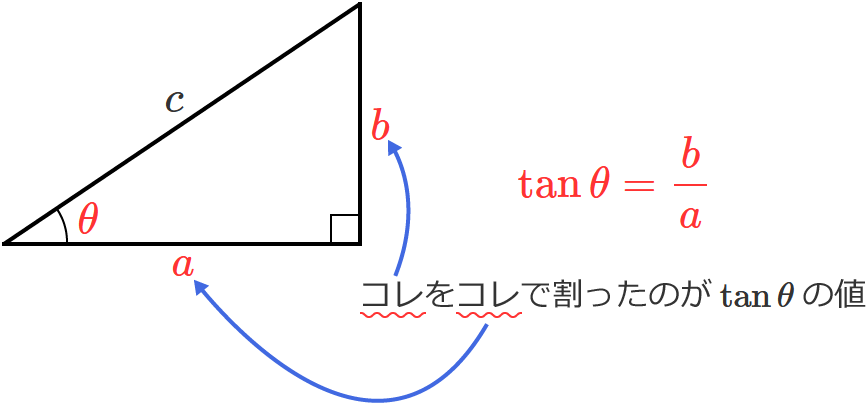
$\tan \theta$ が使われるパターン（計算）で多いのは、これまたこんなのですね。

 

次のように直角三角形の辺 $a$ の長さと角度 $\theta$だけが分かっているとします。このとき、辺 $b$ の長さはいくら？

 

 

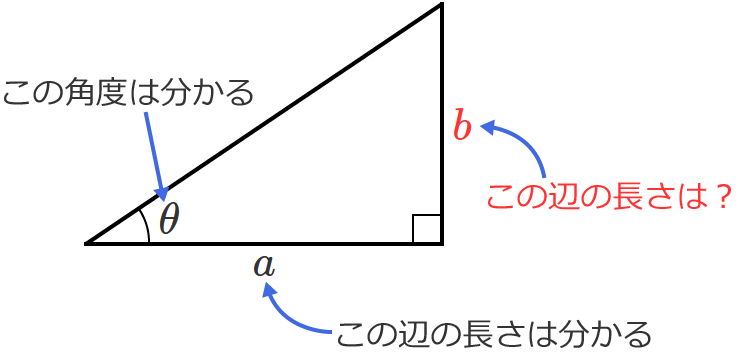
これまた先ほどの③式から簡単に分かります。

 

③式は、$\tan \theta = \dfrac{b}{a}$ でした。

 

これを変形すると、$b = a \times \tan \theta$ となり、辺の長さ $a$ と角度 $\theta$ が分かれば辺の長さ $b$ を求めることができます。（ $\tan \theta$ の値は角度（ $\theta$ ）によって値が決まります。）

 

以上が $\sin$ 、$\cos$ 、$\tan$ の基本になりますが、どの辺の長さをどの辺の長さで割れば何（ $\sin$ 、$\cos$ 、$\tan$ ）なのか？　おぼえておくようにしましょう。

 

あ、それから、三平方の定理ってありますよね？　ピタゴラスの定理とも呼ばれる定理で、直角三角形の斜辺の長さを求めるときなどに使う定理で、こんなの。

 

 

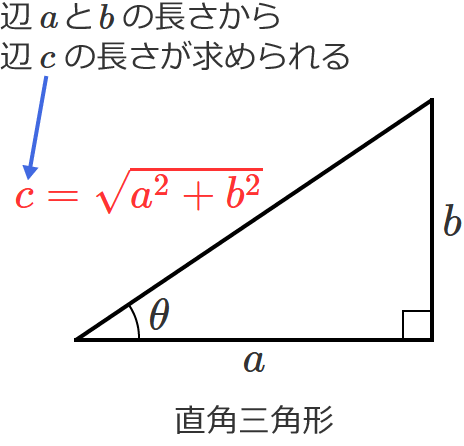
この三平方の定理を使うと、$\sin \theta$ 、$\cos \theta$ は次のようにも表わすことができます。

 

$\sin \theta = \dfrac{b}{\sqrt{a^2 + b^2}}$　、　$\cos \theta = \dfrac{a}{\sqrt{a^2 + b^2}}$

 

この2つも一緒におぼえておきましょう！

 

 

三角関数のsinθ、cosθ、tanθの公式のおぼえ方

ついでなので、三角関数の $\sin \theta$ 、$\cos \theta$ 、$\tan \theta$ の公式のおぼえ方を紹介します。

 

と言っても特別変わったおぼえ方ではないので、たぶん、みなさんこのおぼえ方で学校で習うのではないでしょうか？

 

まずは $\sin \theta$ の公式のおぼえ方です。

 

sinθの公式のおぼえ方

$\sin \theta$ はアルファベットの「$\mathrm{s}$」で始まりますが、この「$\mathrm{s}$」を筆記体の小文字で書くと、

 

 

ですよね。なので、次のようにおぼえます。

 

 

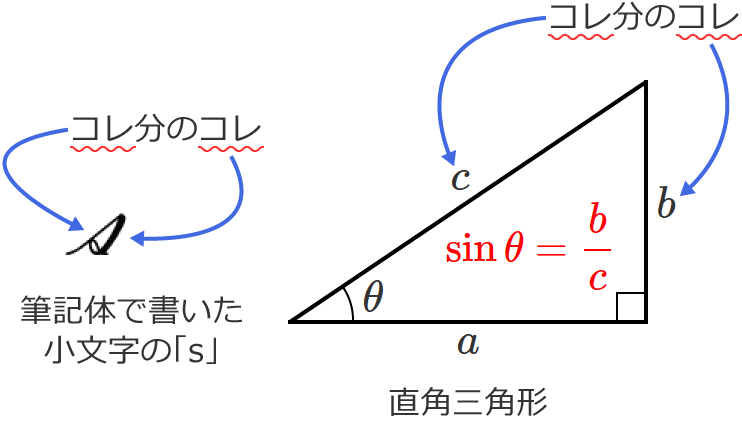
アルファベットの筆記体の小文字の「$\mathrm{s}$」と直角三角形を対応させているんですね。$\sin \theta$ の公式はアルファベットの筆記体の小文字の「$\mathrm{s}$」とおぼえましょう。

 

次は $\cos \theta$ の公式のおぼえ方です。

 

cosθの公式のおぼえ方

$\cos \theta$ はアルファベットの「$\mathrm{c}$」で始まりますが、この「$\mathrm{c}$」と直角三角形を対応させておぼえます。

 

 

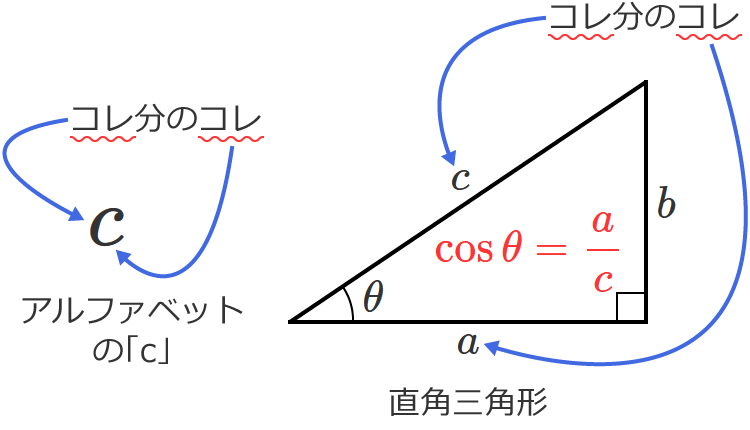
$\cos \theta$ の公式はアルファベットの「$\mathrm{c}$」とおぼえましょう。

 

最後は $\tan \theta$ の公式のおぼえ方です。

 

tanθの公式のおぼえ方

$\tan \theta$ はアルファベットの「$\mathrm{t}$」で始まりますが、この「$\mathrm{t}$」を筆記体の小文字で書くと、

 

 

ですよね。なので、次のようにおぼえます。

 

 

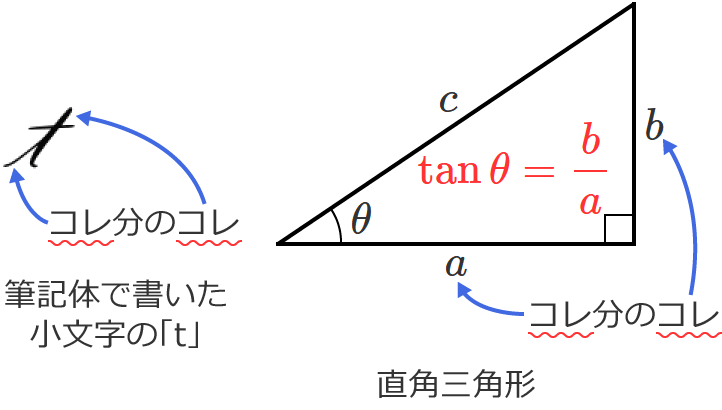
アルファベットの筆記体の小文字の「$\mathrm{t}$」と直角三角形を対応させているんですね。$\tan \theta$ の公式はアルファベットの筆記体の小文字の「$\mathrm{t}$」とおぼえましょう。

 

 

 

三角関数の公式・定理　←BACK

NEXT→　電気数学のお勉強

スポンサーリンク

三角関数のsin、cos、tanって何？　関連ページ

三角関数の公式・定理

電気数学で使われる三角関数sin（サイン）、cos（コサイン）、tan（タンジェント）などの公式・定理についてまとめています。三角関数は電気の計算でよく使われる関数ですので、公式・定理をおぼえておくようにしましょう。