スポンサーリンク
三角関数の公式・定理
※ページ内にPR・広告が含まれる場合があります。
三角関数の公式・定理についてまとめてみました。
三角関数は電気の計算でもよく使われる関数で電気数学の基本になりますので、公式と定理はおぼえておくようにしましょう。
sin、cos、tanの基本公式
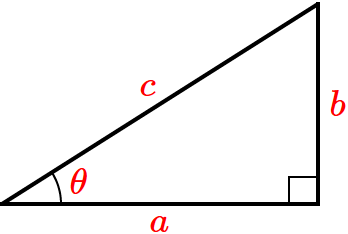
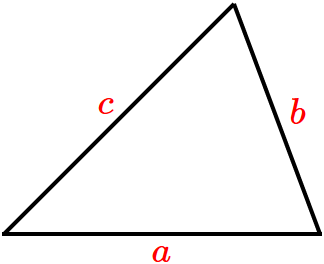
● $\sin\theta =\dfrac{b}{c}$
● $\cos\theta =\dfrac{a}{c}$
● $\tan\theta =\dfrac{b}{a}$
● $\tan\theta =\dfrac{\sin\theta}{\cos\theta}$
● $\sin\left(\theta +2\pi n\right) =\sin\theta$ ($n$ は整数)
● $\cos\left(\theta +2\pi n\right) =\cos\theta$ ($n$ は整数)
● $\tan\left(\theta +\pi n\right) =\tan\theta$ ($n$ は整数)
● $\sin\left( -\theta\right) =-\sin\theta$
● $\cos\left( -\theta\right) =\cos\theta$
● $\tan\left( -\theta\right) =-\tan\theta$
● $\sin\left(\theta +\dfrac{\pi}{2}\right) =\cos\theta$
● $\cos\left(\theta +\dfrac{\pi}{2}\right) =-\sin\theta$
● $\tan\left(\theta +\dfrac{\pi}{2}\right) =-\dfrac{1}{\tan\theta}$
● $\sin\left(\theta +\pi\right) =-\sin\theta$
● $\cos\left(\theta +\pi\right) =-\cos\theta$
● $\tan\left(\theta +\pi\right) =\tan\theta$
● $\sin\left(\theta -\dfrac{\pi}{2}\right) =-\cos\theta$
● $\cos\left(\theta -\dfrac{\pi}{2}\right) =\sin\theta$
● $\tan\left(\theta -\dfrac{\pi}{2}\right) =-\dfrac{1}{\tan\theta}$
● $\sin\left(\theta -\pi\right) =-\sin\theta$
● $\cos\left(\theta -\pi\right) =-\cos\theta$
● $\tan\left(\theta -\pi\right) =\tan\theta$
● $\sin\left(\dfrac{\pi}{2} -\theta\right) =\cos\theta$
● $\cos\left(\dfrac{\pi}{2} -\theta\right) =\sin\theta$
● $\tan\left(\dfrac{\pi}{2} -\theta\right) =\cot\theta =\dfrac{1}{\tan\theta}$
● $\sin\left(\pi -\theta\right) =\sin\theta$
● $\cos\left(\pi -\theta\right) =-\cos\theta$
● $\tan\left( \pi -\theta\right) =-\tan\theta$
● $\sin^2\theta +\cos^2\theta =1$
● $\tan^2\theta +1=\dfrac{1}{\cos^2\theta}$
cosec、sec、cotの公式
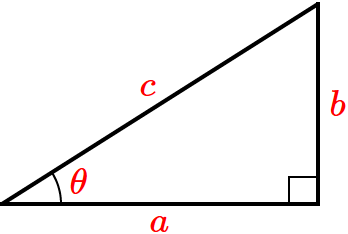
● $\mathrm{cosec}\,\theta =\dfrac{1}{\sin\theta} =\dfrac{c}{b}$
● $\sec\theta =\dfrac{1}{\cos\theta} =\dfrac{c}{a}$
● $\cot\theta =\dfrac{1}{\tan\theta} =\dfrac{a}{b}$
正弦定理
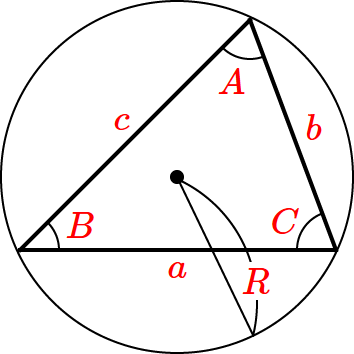
● $\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R$
余弦定理
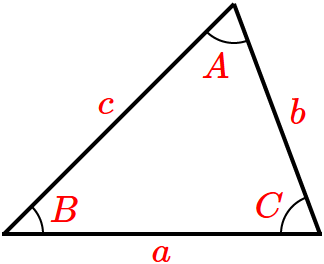
● $a^2=b^2+c^2-2bc\cos A$
● $b^2=a^2+c^2-2ac\cos B$
● $c^2=a^2+b^2-2ab\cos C$
加法定理
● $\sin\left(\alpha\pm\beta\right)$ $=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta$ (複合同順)
● $\cos\left(\alpha\pm\beta\right)$ $=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta$ (複合同順)
● $\tan\left(\alpha\pm\beta\right) =\dfrac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}$ (複合同順)
倍角の公式
● $\sin 2\alpha =2\sin\alpha\cos\alpha$
● $\cos 2\alpha =\cos^2\alpha -\sin^2\alpha$
● $\cos 2\alpha =2\cos^2\alpha -1$
● $\cos 2\alpha =1-2\sin^2\alpha$ $\left(\sin^2\alpha =\dfrac{1-\cos 2\alpha}{2}\right)$
● $\tan 2\alpha =\dfrac{2\tan\alpha}{1-\tan^2\alpha}$
半角の公式
● $\sin^2\dfrac{\alpha}{2} =\dfrac{1-\cos\alpha}{2}$
● $\cos^2\dfrac{\alpha}{2} =\dfrac{1+\cos\alpha}{2}$
● $\tan^2\dfrac{\alpha}{2} =\dfrac{1-\cos\alpha}{1+\cos\alpha}$
積和の公式(積を和(または差)に変換)
● $\sin\alpha\cos\beta$ $=\dfrac{\sin\left(\alpha +\beta\right) +\sin\left(\alpha -\beta\right)}{2}$
● $\cos\alpha\sin\beta$ $=\dfrac{\sin\left(\alpha +\beta\right) -\sin\left(\alpha -\beta\right)}{2}$
● $\sin\alpha\sin\beta$ $=\dfrac{\cos\left(\alpha -\beta\right) -\cos\left(\alpha +\beta\right)}{2}$
● $\cos\alpha\cos\beta$ $=\dfrac{\cos\left(\alpha +\beta\right) +\cos\left(\alpha -\beta\right)}{2}$
和積の公式(和(または差)を積に変換)
● $\sin A+\sin B$ $=2\sin\left(\dfrac{A+B}{2}\right)\cos\left(\dfrac{A-B}{2}\right)$
● $\sin A-\sin B$ $=2\cos\left(\dfrac{A+B}{2}\right)\sin\left(\dfrac{A-B}{2}\right)$
● $\cos A+\cos B$ $=2\cos\left(\dfrac{A+B}{2}\right)\cos\left(\dfrac{A-B}{2}\right)$
● $\cos A-\cos B$ $=-2\sin\left(\dfrac{A+B}{2}\right)\sin\left(\dfrac{A-B}{2}\right)$
三角関数の合成の公式
● $A\sin\theta +B\cos\theta$ $=\sqrt{A^2+B^2}\sin\left(\theta +\phi\right)$
● $A\cos\theta -B\sin\theta$ $=\sqrt{A^2+B^2}\cos\left(\theta +\phi\right)$
ただし、$\phi =\tan^{-1}\dfrac{B}{A}$
ヘロンの公式(三辺から三角形の面積を求める公式)
● $S=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}$
ただし、$s=\dfrac{a+b+c}{2}$
スポンサーリンク
スポンサーリンク
電気数学のお勉強 ←BACK
スポンサーリンク
三角関数の公式・定理 関連ページ
- 三角関数のsin、cos、tanって何?
- 電気数学で使われる三角関数のsin(サイン)、cos(コサイン)、tan(タンジェント)についてまとめています。三角関数は電気の計算でよく使われる関数ですので、まずは三角関数の基本であるsinθ、cosθ、tanθの公式と使い方をおぼえましょう。

