電気のお勉強｜直流回路｜分圧の法則による直流回路の計算

スポンサーリンク

次の図のように、電源電圧 $V$［$ \mathrm{V} $］に「抵抗 $R_1$」と「抵抗 $R_2$ と $R_3$ の並列接続」が直列に接続されている回路について考えます。

 

 

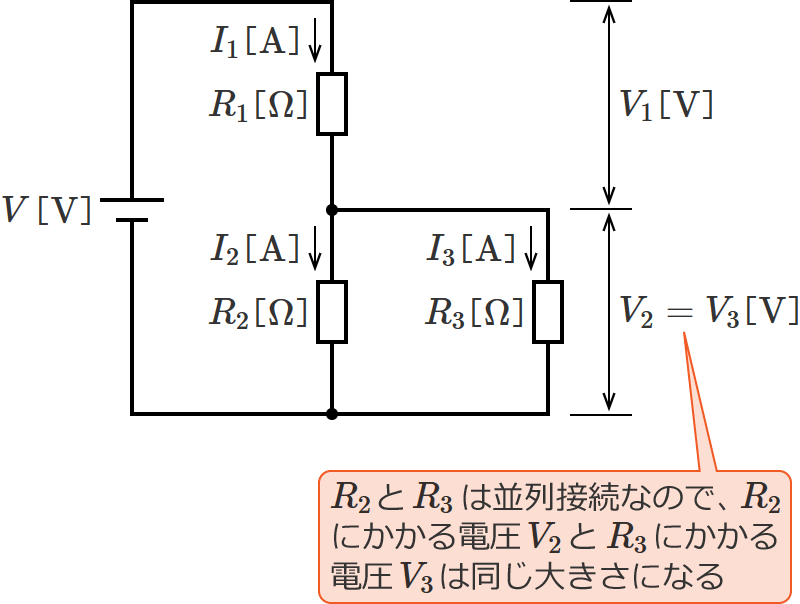
この回路において、各抵抗 $R_1$ 、$R_2$ 、$R_3$ にかかる電圧 $V_1$ 、$V_2$ 、$V_3$ 、および各抵抗 $R_1$ 、$R_2$ 、$R_3$ に流れる電流 $I_1$ 、$I_2$ 、$I_3$ を分圧の法則を使って求めてみます。

 

まず、抵抗 $R_2$ と $R_3$ を合成し、合成後の抵抗を $R_0$ 、合成抵抗 $R_0$ にかかる電圧を $V_0$ とすると、上の回路図は次のようになります。

 

 

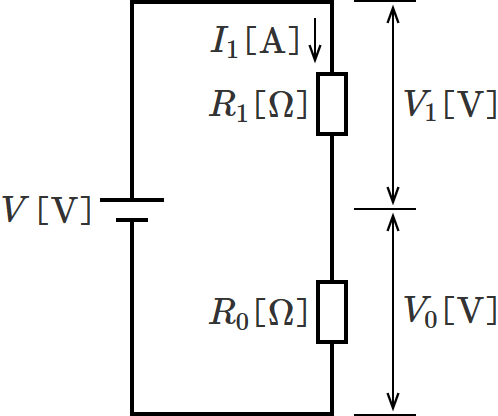
すると、抵抗 $R_1$ と $R_0$ が直列に接続された回路になるので、電圧 $V_1$ と $V_0$ は分圧の法則よりそれぞれ次式となります。

 

$V_1 = V \times \dfrac{R_1}{R_1 + R_0}$　　$\therefore V_1 = \dfrac{R_1 V}{R_1 + R_0}$　…①

 

$V_0 = V \times \dfrac{R_0}{R_1 + R_0}$　　$\therefore V_0 = \dfrac{R_0 V}{R_1 + R_0}$　…②

 

ここで、抵抗 $R_0$ は抵抗 $R_2$ と $R_3$ の並列合成抵抗なので、抵抗 $R_0$ は次式で与えられます。

 

$R_0 = \dfrac{R_2 R_3}{R_2 + R_3}$　…③

 

③を①式に代入すると、

 

$V_1 = \dfrac{R_1 V}{R_1 + \dfrac{R_2 R_3}{R_2 + R_3}}$ $= \dfrac{R_1 V}{\dfrac{R_1 \left( R_2 +R_3 \right) + R_2 R_3}{R_2 + R_3}}$ $= \dfrac{R_1 \left( R_2 + R_3 \right) V}{R_1 R_2 + R_1 R_3 + R_2 R_3}$

 

 

③を②式に代入すると、

 

$V_0 = \dfrac{\dfrac{R_2 R_3}{R_2 + R_3} V}{R_1 + \dfrac{R_2 R_3}{R_2 + R_3}}$ $= \dfrac{\dfrac{R_2 R_3}{R_2 + R_3} V}{\dfrac{R_1 \left( R_2 +R_3 \right) + R_2 R_3}{R_2 + R_3}}$ $= \dfrac{R_2 R_3 V}{R_1 R_2 + R_1 R_3 + R_2 R_3}$

 

$\therefore V_0 = \dfrac{R_2 R_3 V}{R_1 R_2 + R_2 R_3 + R_1 R_3}$

 

この電圧 $V_0$ は、抵抗 $R_2$ 、$R_3$ の電圧 $V_2$ 、$V_3$ に等しいので、
（$\because$ $R_0$ は $R_2$ と $R_3$ の並列合成抵抗）

 

 

となります。

 

以上④、⑤より、電圧 $V_1$ 、$V_2$ 、$V_3$ が求められたので、次に電流 $I_1$ 、$I_2$ 、$I_3$ を求めます。

 

$I_1 = \dfrac{V_1}{R_1}$ $= \dfrac{1}{R_1} \cdot \dfrac{R_1 \left( R_2 + R_3 \right) V}{R_1 R_2 + R_2 R_3 + R_1 R_3}$ $= \dfrac{\left( R_2 + R_3 \right) V}{R_1 R_2 + R_2 R_3 + R_1 R_3}$

 

 

$I_2 = \dfrac{V_2}{R_2}$ $= \dfrac{1}{R_2} \cdot \dfrac{R_2 R_3 V}{R_1 R_2 + R_2 R_3 + R_1 R_3}$ $= \dfrac{R_3 V}{R_1 R_2 + R_2 R_3 + R_1 R_3}$

 

 

$I_3 = \dfrac{V_3}{R_3}$ $= \dfrac{1}{R_3} \cdot \dfrac{R_2 R_3 V}{R_1 R_2 + R_2 R_3 + R_1 R_3}$ $= \dfrac{R_2 V}{R_1 R_2 + R_2 R_3 + R_1 R_3}$

 

 

以上④〜⑧より、抵抗 $R_1$ 、$R_2$ 、$R_3$ にかかる電圧と流れる電流を分圧の法則から求めることができました。

 

 

このページの回路と同じ回路を、分流の法則による直流回路の計算のページでは分流の法則を使って、また、ループ解析（基本）のページではループ解析を使って計算していますので参考にしてみてください。
直流回路を解く解き方にはいろいろな計算方法があることが分かるかと思います。（もちろん計算結果はどれも同じになります。）

 

そもそも分圧って何でしたっけ？という方は、こちらの直流回路の計算（分圧と分流）のページを参考にしてみてください。

 

合成抵抗の求め方については、こちらの合成抵抗の求め方（計算方法）のページを参考にしてみてください。

ミルマンの定理　←BACK

NEXT→　分流の法則による直流回路の計算

スポンサーリンク

分圧の法則による直流回路の計算　関連ページ

合成抵抗の求め方（計算方法）

合成抵抗の計算は直流回路、交流回路の計算をするときの基本になります。合成抵抗の計算は複雑そうに思えますが、基本的には、抵抗が2個の場合の直列接続または並列接続の合成抵抗の求め方さえ分かっていれば、ほとんどの回路の合成抵抗を求めることができます。

短絡されている抵抗がある場合の合成抵抗の求め方

短絡されている抵抗がある場合の合成抵抗の求め方について解説しています。回路に短絡されている抵抗があるんだけど、どうやって合成抵抗を求めるの？なんてときに参考にしてみてください。

重ね合わせの理

重ね合わせの理について解説しています。重ね合わせの理は、重ね合わせの定理、重ねの理とも呼ばれ、回路に電源が複数ある場合によく使われる定理です。電圧源が2つある回路や、電圧源と電流源が混在した回路などの重ね合わせの理を使った計算方法についても解説していますので参考にしてみてください。

テブナンの定理

テブナンの定理（鳳-テブナンの定理）について解説しています。テブナンの定理は等価電圧源の定理とも呼ばれ、回路の特定の素子に流れる電流を求めるときに有用な定理です。テブナンの定理を使った回路の計算方法や、テブナンの定理の証明についても解説していますので参考にしてみてください。

ノートンの定理

ノートンの定理について解説しています。ノートンの定理は等価電流源の定理とも呼ばれ、回路の特定の素子にかかる電圧を求めるときに有用な定理です。ノートンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。

ミルマンの定理

ミルマンの定理について解説しています。ミルマンの定理は全電圧の定理とも呼ばれ、抵抗と電源の直列接続が複数並列に接続されている回路の端子電圧を求めたいときに有用な定理です。ミルマンの定理の式の導出方法や、ミルマンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。

分流の法則による直流回路の計算

分流の法則を使った直流回路の計算方法の例です。分流の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。

ループ解析（基本）

直流回路の計算をするときによく使われる「ループ解析」の方法と基本的な手順について解説しています。ループ解析はキルヒホッフの第二法則（電圧則）を応用した電気回路の計算方法です。

電圧源と電流源の等価変換

電圧源と電流源の等価変換について解説しています。電圧源と電流源が等価になるための条件や、電圧源から電流源、電流源から電圧源への等価変換のやり方などについて解説していますので参考にしてみてください。

電源から供給できる最大電力（最大有能電力）

電源から供給できる最大電力（最大有能電力）について解説しています。内部抵抗をもつ電源は、負荷に供給できる電力に上限（限界）があります。電源からの供給電力が最大になるための条件や、負荷に供給できる電源の最大電力（最大有能電力）などについて解説していますので、参考にしてみてください。

コンデンサの静電容量と電荷の計算の基本（直列接続と並列接続）

コンデンサの静電容量と電荷の計算の基本についてまとめています。コンデンサの計算は、コンデンサ2個を直列接続または並列接続したときの考え方と計算方法が基本になります。

合成静電容量の求め方（計算方法）

合成静電容量の計算は直流回路、交流回路の計算をするときの基本になります。合成静電容量の計算は複雑そうに思えますが、基本的には、コンデンサが2個の場合の直列接続または並列接続の合成静電容量の求め方さえ分かっていれば、ほとんどの回路の合成静電容量を求めることができます。

ジュール熱とジュールの法則

抵抗や金属などの導体に電流が流れたときに発生するジュール熱と、ジュールの法則について解説しています。ジュール熱が発生する理由（原理）についても解説していますので、ジュール熱・ジュールの法則の勉強の参考にしてみてください。