コンデンサの静電容量と電荷の計算の基本（直列接続と並列接続）

※ページ内にPR･広告が含まれる場合があります。

コンデンサが直列に接続された場合や並列に接続された場合のコンデンサの静電容量、コンデンサに蓄えられる電荷についての問題は、電験三種の理論でもよく出題されていて、電気回路の計算の基礎的なところになります。

このページでは、コンデンサが1個の場合、直列接続の場合、並列接続の場合のコンデンサの静電容量とコンデンサに蓄えられる電荷の基本的な考え方、計算方法について解説します。

コンデンサが1個のときのコンデンサの静電容量と蓄えられる電荷

コンデンサが1個のときの計算（式）がコンデンサの静電容量と電荷の計算をするときの基本になりますので、まずはコンデンサが1個の場合からいってみましょう。

コンデンサが1個のときのコンデンサの静電容量

コンデンサが1個のときのコンデンサの静電容量は、次の図のようにコンデンサの静電容量を $C$［$ \mathrm{F} $］、誘電体の誘電率を $\varepsilon$［$ \mathrm{F / m} $］、電極板面積を $S$［$ \mathrm{m^2} $］、電極板間隔を $d$［$ \mathrm{m} $］とすると、

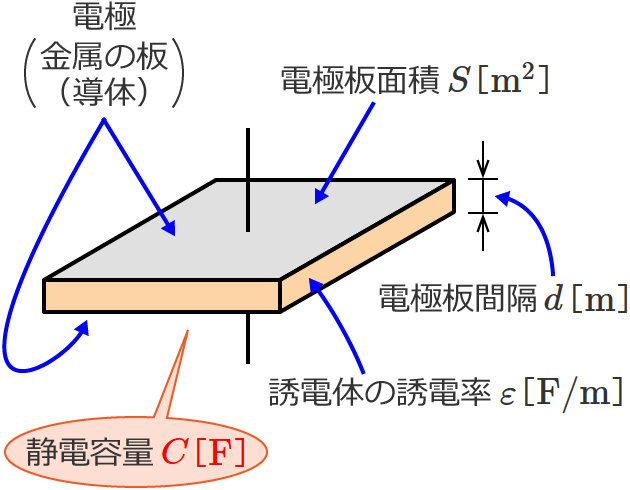
コンデンサの各値の説明図

次の式で与えられます。

$C = \varepsilon \dfrac{S}{d}$　［$ \mathrm{F} $］　…①　（←コンデンサの静電容量の公式）

①式を見ると分かるように、コンデンサの静電容量 $C$ は、誘電体の誘電率 $\varepsilon$ と電極板面積 $S$ に比例し、電極板間隔 $d$ に反比例します。

したがって、コンデンサの静電容量 $C$ は、誘電体の誘電率 $\varepsilon$ または電極板面積 $S$ が大きくなると大きくなり、電極板間隔 $d$ が大きくなると小さくなります。

この静電容量の公式は、次の電荷の公式（ $Q = CV$ ）とともにコンデンサの計算をするときの基本になるので、必ずおぼえておきましょう。

コンデンサが1個のときのコンデンサに蓄えられる電荷

次の図のように、1個のコンデンサに直流電圧 $V$［$ \mathrm{V} $］をかけてみます。

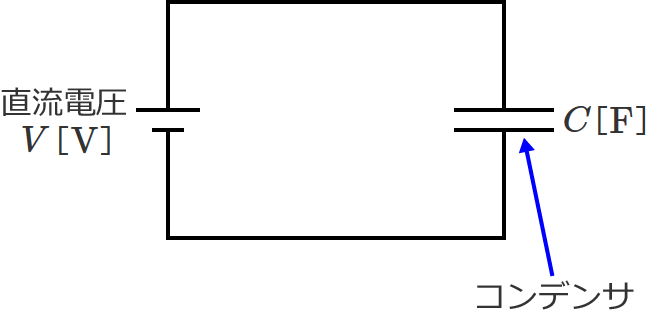
コンデンサ1個に電圧Vを印加

すると、コンデンサは直流電流を流すことができないので回路に電流は流れません※が、コンデンサには電荷が蓄えられます。

厳密に言えば、コンデンサに電荷が貯まりきるまでの時間であれば直流であっても電流は流れます。この電荷が貯まりきるまでに流れる電流について詳しく知りたい方はRC直列回路の過渡現象のページを参考にしてみてください。

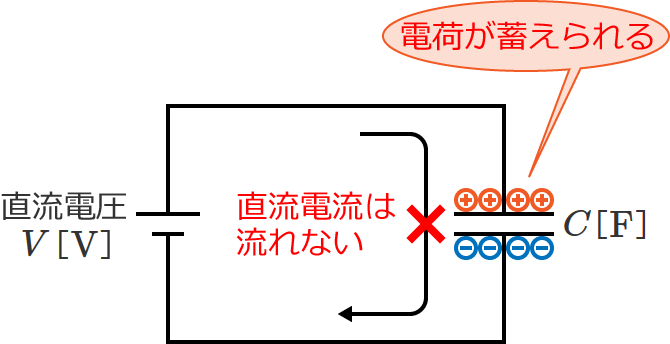
コンデンサには直流電流は流れないが電荷が蓄えられる

このときの蓄えられる電荷の大きさを $Q$［$ \mathrm{C} $］とすると、$Q$ は次の式で与えられます。

$Q = CV$　［$ \mathrm{C} $］　…②　（←コンデンサの電荷の公式）

コンデンサにQ［C］の電荷が蓄えらえる

②式を見ると分かるように、コンデンサに蓄えられる電荷 $Q$ は、コンデンサの静電容量 $C$ とコンデンサにかかる電圧 $V$ に比例します。

したがって、コンデンサに蓄えられる電荷 $Q$ は、コンデンサの静電容量 $C$ またはコンデンサにかかる電圧 $V$ が大きくなると大きくなります。

以上のように、コンデンサが1個のときのコンデンサの静電容量と蓄えられる電荷は、公式そのままで計算できます。公式をおぼえておくだけでいいので簡単ですね。

コンデンサの静電容量と電荷の公式

コンデンサが直列接続されているときのコンデンサの静電容量と蓄えられる電荷

次は、コンデンサ2個が直列接続されているときのコンデンサの静電容量と蓄えられる電荷についてです。

コンデンサが2個直列接続されているときのコンデンサの静電容量（合成静電容量）

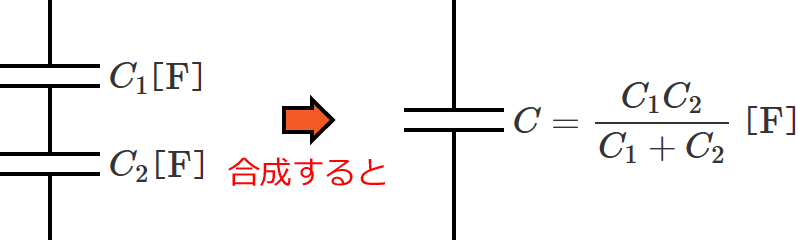
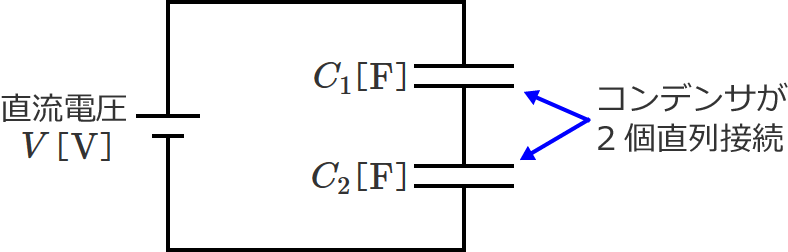
2つのコンデンサの静電容量をそれぞれ $C_1$［$ \mathrm{F} $］、$C_2$［$ \mathrm{F} $］として、コンデンサ $C_1$ と $C_2$ を直列接続すると次のようになります。

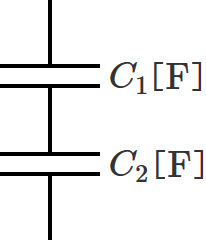
コンデンサが2個直列接続されたときの回路図

このとき、2つのコンデンサの静電容量を合成した合成静電容量は、どうやって求めればいいでしょうか？

コンデンサが2個直列接続されているときの合成静電容量は、2つの静電容量を和分の積すると求めることができます。

・・・、え？　なんか変？

そう、変（？）なんです。コンデンサの合成静電容量を求めるときと抵抗の合成抵抗を求めるときでは、求め方（和分の積か？ただ足すだけか？）が逆になります。

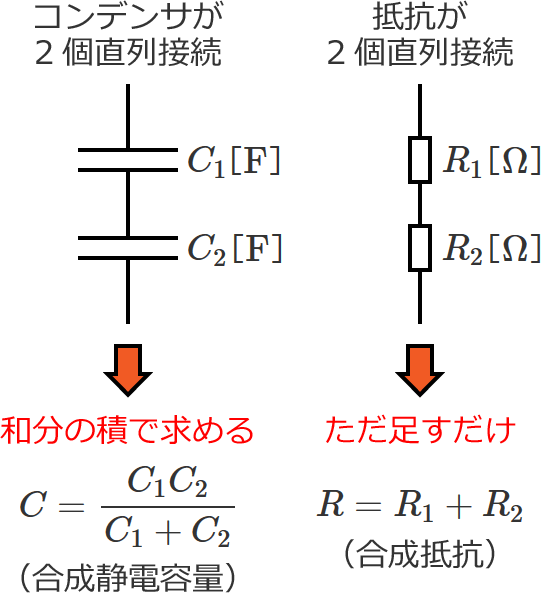
コンデンサの合成静電容量と抵抗の合成抵抗の求め方の違い（直列接続）

なので、コンデンサが2個直列接続されているときの合成静電容量 $C$ は、2つの静電容量（ $C_1$ 、$C_2$ ）を和分の積して、

$C = \dfrac{C_1 C_2}{C_1 + C_2}$　［$ \mathrm{F} $］

となります。

コンデンサが2個直列接続のときの合成静電容量

補足

コンデンサが3個以上直列接続されているときの合成静電容量

コンデンサが2個直列接続のときの合成静電容量は和分の積で求められますが、3個以上になると和分の積では求められません。3個以上のときは次の式で求めましょう。

$\dfrac{1}{C} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + \dfrac{1}{C_3} + \cdots + \dfrac{1}{C_n}$

（抵抗が3個以上並列接続されているときの合成抵抗を求めるときと同じ形の式になります。）

コンデンサの合成静電容量については、こちらの合成静電容量の求め方（計算方法）のページにまとめていますので、こちらも参考にしてみてください。

コンデンサが2個直列接続されているときのコンデンサに蓄えられる電荷

コンデンサが直列接続されているときの電荷

2個直列接続されているコンデンサに直流電圧 $V$［$ \mathrm{V} $］をかけてみます。すると、コンデンサ $C_1$ と $C_2$ には図のように電荷が蓄えられ、このときに蓄えられる電荷の大きさは $C_1$ と $C_2$ で同じ大きさになります。

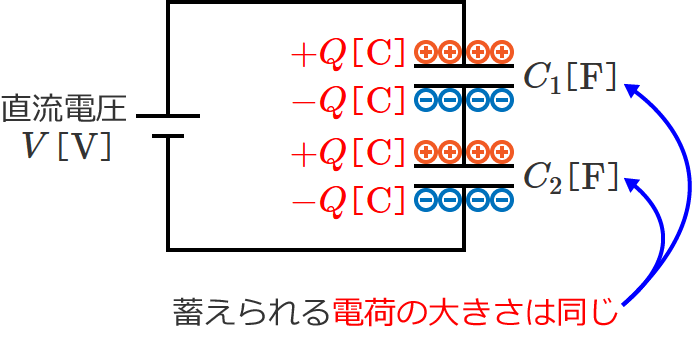
直列接続されたコンデンサに蓄えられる電荷の大きさは同じ

ちなみに、コンデンサが3つ、4つ…と増えても、各コンデンサに蓄えられる電荷の大きさはどれも同じになります。

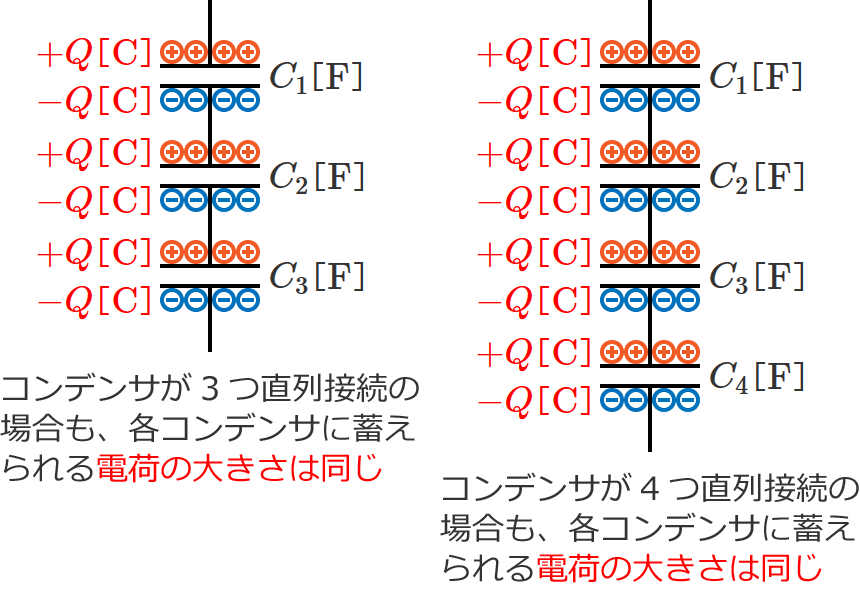
コンデンサが3個、4個直列接続のときの各コンデンサの電荷

この、

コンデンサが直列接続の場合には各コンデンサに蓄えられる電荷の大きさは同じになる

というのが、コンデンサの直列接続回路を考えるときの大事なポイント（基本！）になるので、必ずおぼえておきましょう。（これさえ分かっていれば、コンデンサの直列接続の問題は解けます！たぶん。）

コンデンサが2個直列接続されているときの電荷の計算

では、コンデンサが2個直列接続されているときのコンデンサに蓄えられる電荷の大きさを計算してみます。

コンデンサが2個直列接続のときの回路図

コンデンサ $C_1$ 、$C_2$ に蓄えられる電荷をそれぞれ $Q_1$ 、$Q_2$ とし、コンデンサ $C_1$ 、$C_2$ の電圧をそれぞれ $V_1$ 、$V_2$ とします。

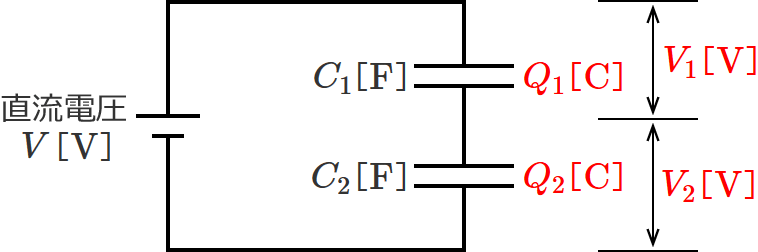
未知数を書き込んだコンデンサの直列回路の回路図

この回路図を見て、分かるところから式をたてて計算すれば、コンデンサに蓄えられる電荷の大きさを求めることができます。

この回路の電源電圧は $V$ で、その電圧 $V$ がコンデンサ $C_1$ と $C_2$ に分圧されるので、次の式が成り立ちます。

$V = V_1 + V_2$　…①

それから、コンデンサ $C_1$ のところを見ると、コンデンサ $C_1$ の電圧は $V_1$ なので、ここにコンデンサの電荷の公式（ $Q = CV$ ）をあてはめます。すると、

$Q_1 = C_1 V_1$　…②　となります。

同じようにコンデンサ $C_2$ のところにもコンデンサの電荷の公式（ $Q = CV$ ）をあてはめると、

$Q_2 = C_2 V_2$　…③　となります。

すると、①～③の3つの式ができました。

$\left\{ \begin{array}{l} V = V_1 + V_2 \quad \text{…①} \\ Q_1 = C_1 V_1 \quad \text{…②} \\ Q_2 = C_2 V_2 \quad \text{…③} \end{array} \right.$

この式（①～③の連立方程式）を見ると、未知数が $Q_1$ 、$Q_2$ 、$V_1$ 、$V_2$ の4つで式が3つ・・・

あ、解けません。

連立方程式は「式の数」が「未知数の数」以上ないと解けないんです。未知数が4つあるので、もう1つ式がほしいですね。何か式を立てられないでしょうか？

あ、ありました。大事なことを忘れていました。

コンデンサが直列接続されているときには、

コンデンサに蓄えられる電荷の大きさはすべて同じになる

のでした！　なので、次の式も成り立ちますね。

$Q_1 = Q_2$　…④

これで式が4つになりました。

$\left\{ \begin{array}{l} V = V_1 + V_2 \quad \text{…①} \\ Q_1 = C_1 V_1 \quad \text{…②} \\ Q_2 = C_2 V_2 \quad \text{…③} \\ Q_1 = Q_2 \quad \text{…④} \end{array} \right.$
（↑未知数が4つ、式が4つの連立方程式）

未知数が4つ（ $Q_1$ 、$Q_2$ 、$V_1$ 、$V_2$ ）、式が4つなのでこれなら解けますね。では解いていきましょう。

④式より $Q_1 = Q_2$ なので、これを③式に代入して未知数を3つ（ $Q_1$ 、$V_1$ 、$V_2$ ）、式を3つに減らします。

$\left\{ \begin{array}{l} V = V_1 + V_2 \quad \text{…①} \\ Q_1 = C_1 V_1 \quad \text{…②} \\ Q_1 = C_2 V_2 \quad \text{…③’} \end{array} \right.$
（↑未知数が3つ、式が3つの連立方程式）

③’を②式に代入して、未知数を2つ（ $V_1$ 、$V_2$ ）、式を2つに減らします。

$\left\{ \begin{array}{l} V = V_1 + V_2 \quad \text{…①} \\ C_1 V_1 = C_2 V_2 \quad \text{…②’} \end{array} \right.$
（↑未知数が2つ、式が2つの連立方程式）

②’より、$V_1 = \dfrac{C_2 V_2}{C_1}$ なので、これを①式に代入します。すると、

$V = \dfrac{C_2 V_2}{C_1} + V_2$　、　$V = \left( \dfrac{C_2}{C_1} +1 \right) V_2$　、　$V = \left( \dfrac{C_2 + C_1}{C_1} \right) V_2$　、　$V_2 = \left( \dfrac{C_1}{C_1 + C_2} \right) V$

$\therefore V_2 = \dfrac{C_1}{C_1 + C_2} V$　…⑤　（← $V_2$ が求められた）

$V_2$ が求められたので、⑤を①式に代入して $V_1$ を求めます。

$V = V_1 + \dfrac{C_1}{C_1 + C_2} V$　、　$V - \dfrac{C_1}{C_1 + C_2} V = V_1$　、　$V_1 = \left( 1 - \dfrac{C_1}{C_1 + C_2} \right) V$

$V_1 = \left( \dfrac{C_1 + C_2 - C_1}{C_1 + C_2} \right) V$　、　$V_1 = \left( \dfrac{C_2}{C_1 + C_2} \right) V$

$\therefore V_1 = \dfrac{C_2}{C_1 + C_2} V$　…⑥　（← $V_1$ が求められた）

$V_1$ 、$V_2$ が求められたので、次は⑥を②式に代入して $Q_1$ を求めます。すると、

$Q_1 = C_1 V_1 = C_1 \cdot \dfrac{C_2}{C_1 + C_2} V$ $= \dfrac{C_1 C_2}{C_1 + C_2} V$

$\therefore Q_1 = \dfrac{C_1 C_2}{C_1 + C_2} V$　…⑦　（← $Q_1$ が求められた）

④式より $Q_1 = Q_2$ なので $Q_2$ は、

$\therefore Q_2 = \dfrac{C_1 C_2}{C_1 + C_2} V$　…⑧　（← $Q_2$ が求められた）

となります。

以上⑤、⑥、⑦、⑧より、$V_1$ 、$V_2$ 、$Q_1$ 、$Q_2$ が求められました。

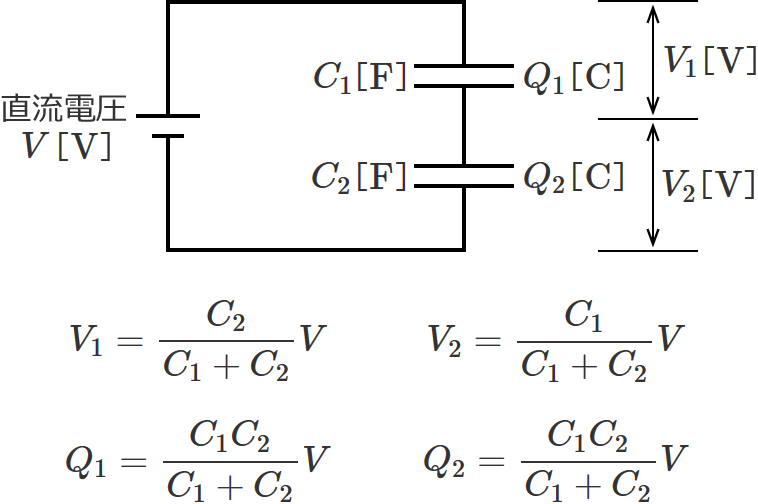
コンデンサの直列接続回路と各値

直列接続されたコンデンサの電荷を求めるときは、このように連立方程式をたてて、それを解いていけばいいです。

連立方程式の解き方（どの式を、どう使って、どの順番で解いていくか）は何パターンもあるので、自分で解きやすい方法を見つけて解いていくようにしましょう。（ここでの連立方程式の解き方は、ちょっとまわりくどい解き方をしています。）

コンデンサが並列接続されているときのコンデンサの静電容量と蓄えられる電荷

次は、コンデンサ2個が並列接続されているときのコンデンサの静電容量と蓄えられる電荷についてです。

コンデンサが2個並列接続されているときのコンデンサの静電容量（合成静電容量）

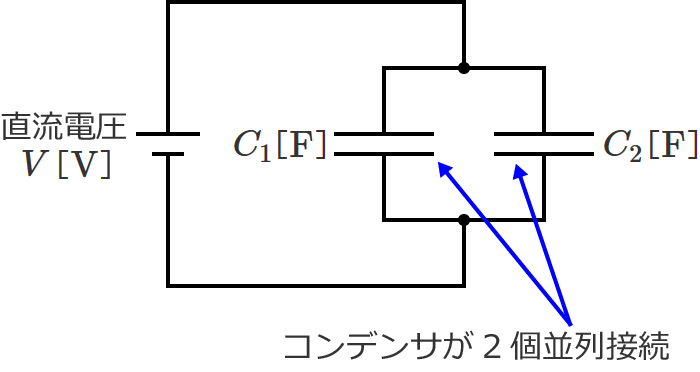
2つのコンデンサの静電容量をそれぞれ $C_1$［$ \mathrm{F} $］、$C_2$［$ \mathrm{F} $］として、コンデンサ $C_1$ と $C_2$ を並列接続すると次のようになります。

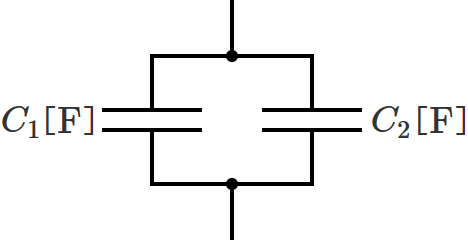
コンデンサが2個並列接続されたときの回路図

このとき、2つのコンデンサの静電容量を合成した合成静電容量は、どうやって求めればいいでしょうか？

コンデンサが2個並列接続されているときの合成静電容量は、2つの静電容量をただ足すだけで求められます。

並列接続の場合も、合成抵抗を求めるときとは求め方（和分の積か？ただ足すだけか？）が逆になります。

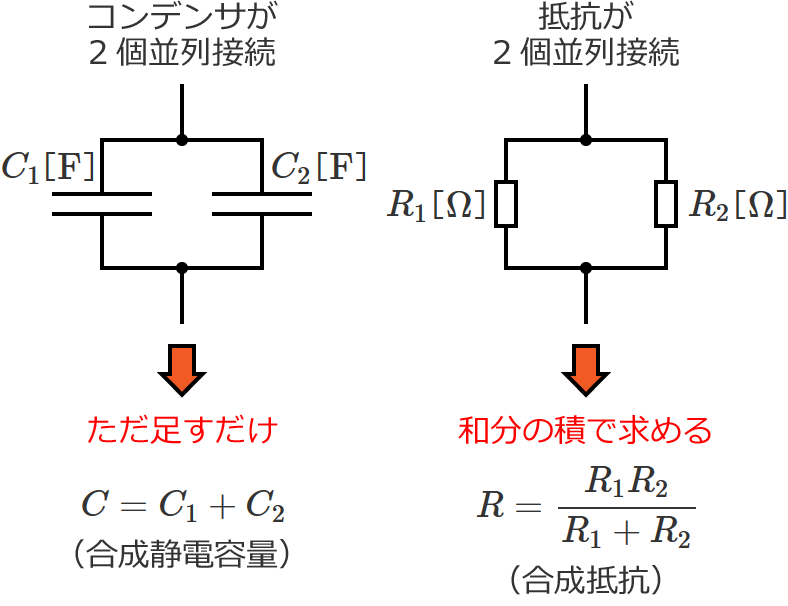
コンデンサの合成静電容量と抵抗の合成抵抗の求め方の違い（並列接続）

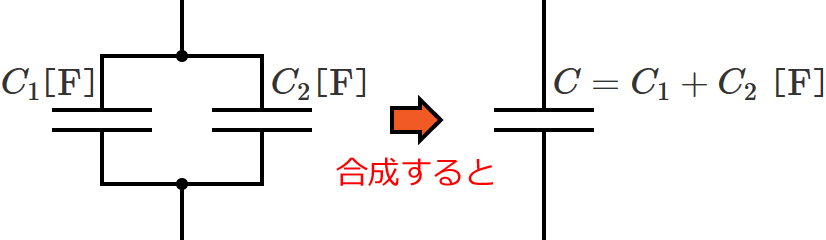
なので、コンデンサが2個並列接続されているときの合成静電容量 $C$ は、2つの静電容量（ $C_1$ 、$C_2$ ）をただ足して、

$C = C_1 + C_2$　［$ \mathrm{F} $］

となります。

コンデンサが2個並列接続のときの合成静電容量

コンデンサが2個並列接続されているときのコンデンサに蓄えられる電荷

コンデンサが並列接続されているときの電荷

2個並列接続されているコンデンサに直流電圧 $V$［$ \mathrm{V} $］をかけてみます。すると、コンデンサ $C_1$ と $C_2$ には図のように電荷が蓄えられ、このときのコンデンサ $C_1$ と $C_2$ の電圧は同じ大きさ $V$［$ \mathrm{V} $］になります。

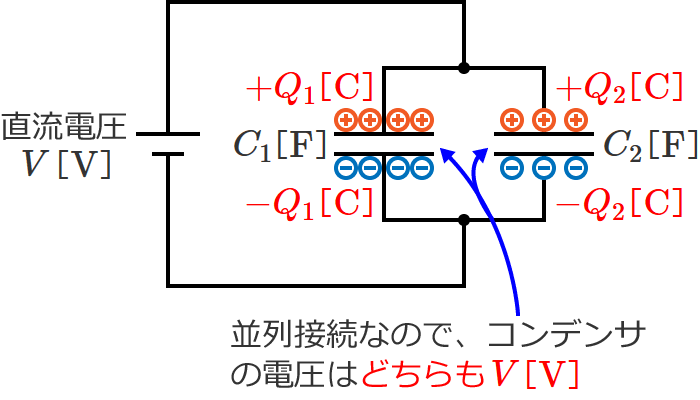
並列接続されたコンデンサの電圧の大きさは同じ

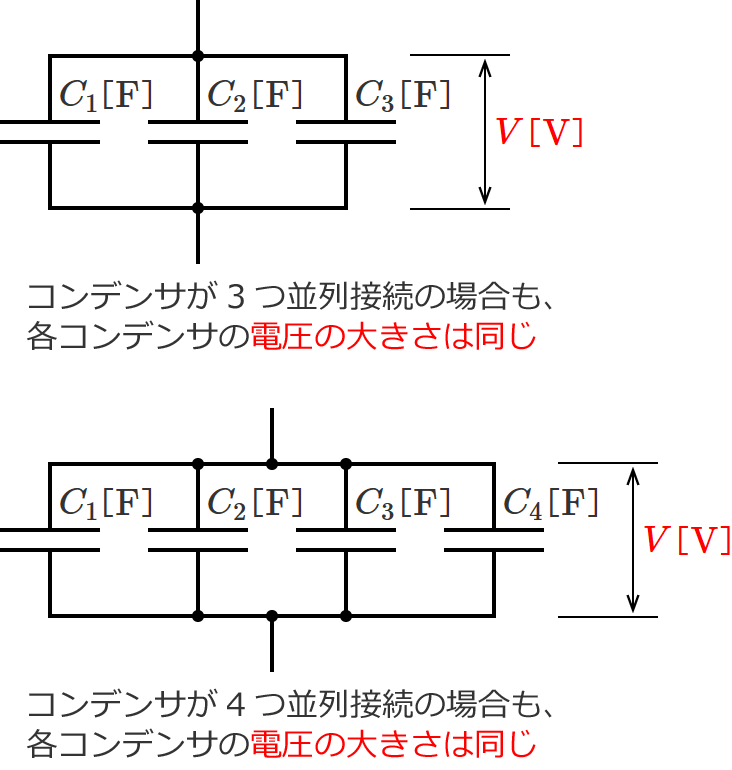
ちなみに、コンデンサが3つ、4つ…と増えても、各コンデンサの電圧の大きさはどれも同じになります。

コンデンサが3個、4個並列接続のときの各コンデンサの電圧

この、

コンデンサが並列接続の場合には各コンデンサの電圧の大きさは同じになる

というのが、コンデンサの並列接続回路を考えるときの大事なポイント（基本！）になるので、必ずおぼえておきましょう。（これさえ分かっていれば、コンデンサの並列接続の問題は解けます！たぶん。）

コンデンサが2個並列接続されているときの電荷の計算

では、コンデンサが2個並列接続されているときのコンデンサに蓄えられる電荷の大きさを計算してみます。

コンデンサが2個並列接続のときの回路図

直列接続のときと同じように、コンデンサ $C_1$ 、$C_2$ に蓄えられる電荷をそれぞれ $Q_1$ 、$Q_2$ とし、コンデンサ $C_1$ 、$C_2$ の電圧をそれぞれ $V_1$ 、$V_2$ とします。（ま、$V_1$ 、$V_2$ は直流電圧 $V$［$ \mathrm{V} $］なんですけどね、とりあえずってことで。）

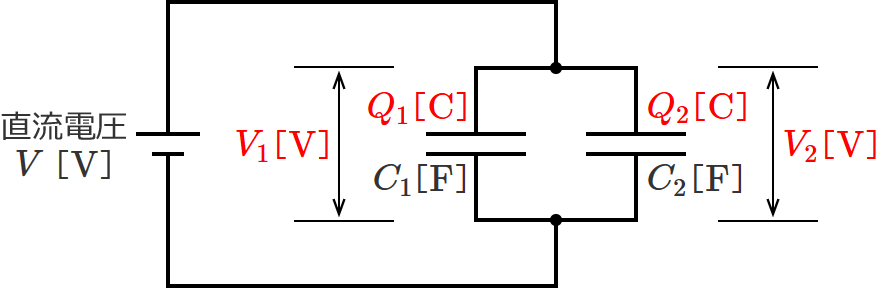
未知数を書き込んだコンデンサの並列回路の回路図

この回路図を見て、分かるところから式をたてて計算していきます。

この回路の電源電圧は $V$ で、その電圧 $V$ がコンデンサ $C_1$ と $C_2$ にそのままかかるので、次の式が成り立ちます。

$V = V_1$　…①

$V = V_2$　…②

それから、コンデンサ $C_1$ のところを見ると $C_1$ にかかる電圧は $V_1$ なので、ここにコンデンサの電荷の公式（ $Q = CV$ ）をあてはめます。すると、

$Q_1 = C_1 V_1$　…③　となります。

同じようにコンデンサ $C_2$ のところにもコンデンサの電荷の公式（ $Q = CV$ ）をあてはめると、

$Q_2 =C_2 V_2$　…④　となります。

すると、①～④の4つの式ができました。

$\left\{ \begin{array}{l} V = V_1 \quad \text{…①} \\ V= V_2 \quad \text{…②} \\ Q_1 = C_1 V_1 \quad \text{…③} \\ Q_2 = C_2 V_2 \quad \text{…④} \end{array} \right.$

この連立方程式は、未知数が4つ（ $Q_1$ 、$Q_2$ 、$V_1$ 、$V_2$ ）、式が4つなので解けますね。では、解いていきましょう。

①、②式より、電圧 $V_1$ 、$V_2$ は $V$ なので、①、②を③、④式に代入します。すると、

$\left\{ \begin{array}{l} Q_1 = C_1 V \quad \text{…③’} \\ Q_2 = C_2 V \quad \text{…④’} \end{array} \right.$

あ、$Q_1$ 、$Q_2$ がでちゃいました。

$\therefore Q_1 = C_1 V$　…③’　（← $Q_1$ が求められた）

$\therefore Q_2 = C_2 V$　…④’　（← $Q_2$ が求められた）

コンデンサの電圧は既に①、②で、でていますね。

$\therefore V_1 = V$　…①　（← $V_1$ が求められた）

$\therefore V_2 = V$　…②　（← $V_2$ が求められた）

以上①、②、③’、④’より、$Q_1$ 、$Q_2$ 、$V_1$ 、$V_2$ が求められました。

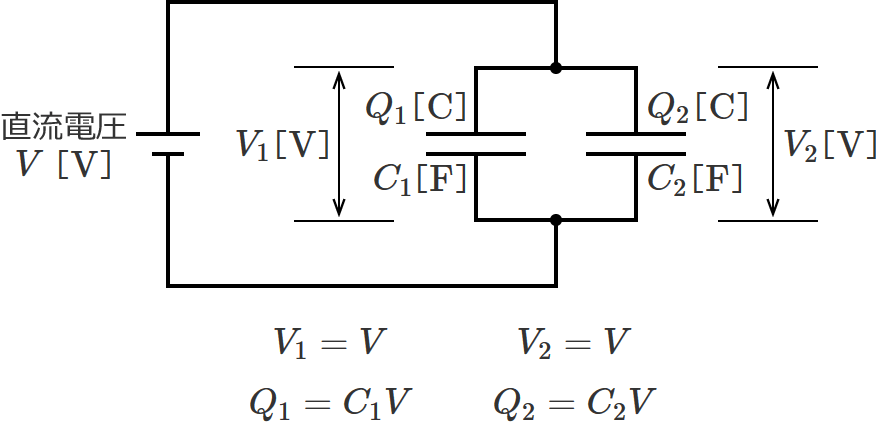
コンデンサの並列接続回路と各値

コンデンサが並列接続のときは、コンデンサ $C_1$ と $C_2$ の電圧がどちらも電圧 $V$ になるので計算も簡単になります。

最後に、コンデンサの静電容量と電荷の計算の基本についてまとめておきます。

コンデンサの静電容量と電荷の計算の基本のまとめ

コンデンサの静電容量の公式： $C = \varepsilon \dfrac{S}{d}$
コンデンサに蓄えられる電荷の公式： $Q = CV$
コンデンサが直列接続のとき、各コンデンサに蓄えられる電荷の大きさは同じになる
コンデンサが並列接続のとき、各コンデンサの電圧の大きさは同じになる

電源から供給できる最大電力（最大有能電力）　←BACK

NEXT→　合成静電容量の求め方（計算方法）

コンデンサの静電容量と電荷の計算の基本（直列接続と並列接続）　関連ページ

合成抵抗の求め方（計算方法）: 合成抵抗の計算は直流回路、交流回路の計算をするときの基本になります。合成抵抗の計算は複雑そうに思えますが、基本的には、抵抗が2個の場合の直列接続または並列接続の合成抵抗の求め方さえ分かっていれば、ほとんどの回路の合成抵抗を求めることができます。
短絡されている抵抗がある場合の合成抵抗の求め方: 短絡されている抵抗がある場合の合成抵抗の求め方について解説しています。回路に短絡されている抵抗があるんだけど、どうやって合成抵抗を求めるの？なんてときに参考にしてみてください。
重ね合わせの理: 重ね合わせの理について解説しています。重ね合わせの理は、重ね合わせの定理、重ねの理とも呼ばれ、回路に電源が複数ある場合によく使われる定理です。電圧源が2つある回路や、電圧源と電流源が混在した回路などの重ね合わせの理を使った計算方法についても解説していますので参考にしてみてください。
テブナンの定理: テブナンの定理（鳳-テブナンの定理）について解説しています。テブナンの定理は等価電圧源の定理とも呼ばれ、回路の特定の素子に流れる電流を求めるときに有用な定理です。テブナンの定理を使った回路の計算方法や、テブナンの定理の証明についても解説していますので参考にしてみてください。
ノートンの定理: ノートンの定理について解説しています。ノートンの定理は等価電流源の定理とも呼ばれ、回路の特定の素子にかかる電圧を求めるときに有用な定理です。ノートンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。
ミルマンの定理: ミルマンの定理について解説しています。ミルマンの定理は全電圧の定理とも呼ばれ、抵抗と電源の直列接続が複数並列に接続されている回路の端子電圧を求めたいときに有用な定理です。ミルマンの定理の式の導出方法や、ミルマンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。
分圧の法則による直流回路の計算: 分圧の法則を使った直流回路の計算方法の例です。分圧の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。
分流の法則による直流回路の計算: 分流の法則を使った直流回路の計算方法の例です。分流の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。
ループ解析（基本）: 直流回路の計算をするときによく使われる「ループ解析」の方法と基本的な手順について解説しています。ループ解析はキルヒホッフの第二法則（電圧則）を応用した電気回路の計算方法です。
電圧源と電流源の等価変換: 電圧源と電流源の等価変換について解説しています。電圧源と電流源が等価になるための条件や、電圧源から電流源、電流源から電圧源への等価変換のやり方などについて解説していますので参考にしてみてください。
電源から供給できる最大電力（最大有能電力）: 電源から供給できる最大電力（最大有能電力）について解説しています。内部抵抗をもつ電源は、負荷に供給できる電力に上限（限界）があります。電源からの供給電力が最大になるための条件や、負荷に供給できる電源の最大電力（最大有能電力）などについて解説していますので、参考にしてみてください。
合成静電容量の求め方（計算方法）: 合成静電容量の計算は直流回路、交流回路の計算をするときの基本になります。合成静電容量の計算は複雑そうに思えますが、基本的には、コンデンサが2個の場合の直列接続または並列接続の合成静電容量の求め方さえ分かっていれば、ほとんどの回路の合成静電容量を求めることができます。
ジュール熱とジュールの法則: 抵抗や金属などの導体に電流が流れたときに発生するジュール熱と、ジュールの法則について解説しています。ジュール熱が発生する理由（原理）についても解説していますので、ジュール熱・ジュールの法則の勉強の参考にしてみてください。

電気のお勉強｜直流回路｜コンデンサの静電容量と電荷の計算の基本（直列接続と並列接続）