電気のお勉強｜直流回路｜ループ解析（基本）

スポンサーリンク

ループ解析とはキルヒホッフの第二法則（電圧則）を応用した電気回路の解析方法で、このループ解析をおぼえておくと、回路が複雑であっても機械的に解くことができるので実務でも役に立ちます。
（ただし、回路によっては式の数が多くなり、計算がちょっと大変になることもあります。）

 

ちなみに解析とは、電気回路中の各部の電圧、電流を求めることなどをいい「回路を解く」とほぼ同じ意味と考えてもらっていいです。

ループ解析の基本的な手順は、次のようになります。

 

 

それでは、実際にこの手順に従ってループ解析をしてみます。

 

例えば次のような回路があるとして、それぞれの抵抗 $R_1$ 、$R_2$ 、$R_3$ にかかる電圧と、抵抗 $R_1$ 、$R_2$ 、$R_3$ に流れる電流をループ解析で求めます。

 

 

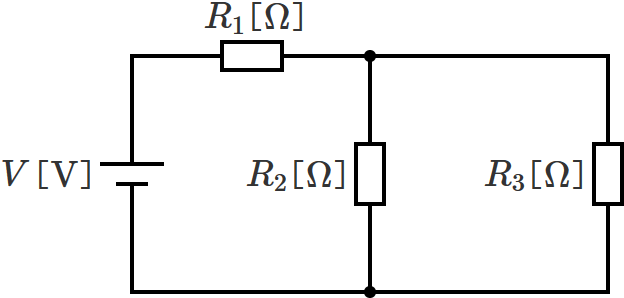
次のようにループ①とループ②を考え、それぞれのループに流れる電流を $I_1$ 、$I_2$ と仮定します。

 

 

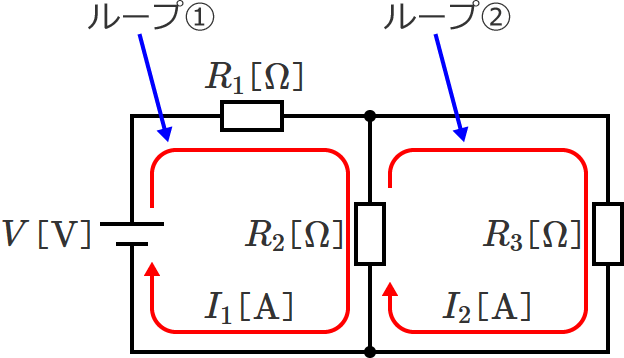
このとき、電流が流れる向き も仮定することに注意してください。ここでは、ループ①、ループ②ともに時計回りを正としています。

 

また、$R_2$ にはループ①の電流とループ②の電流があるので、$R_2$ に実際に流れる電流を求めるときは、ループ①に流れる電流 $I_1$ からループ②に流れる電流 $I_2$ を引いて求めます。

 

ループ①の回路方程式は、次のようになります。

 

$V = R_1 I_1 + R_2 \left( I_1 - I_2 \right)$　…（$\mathrm{A}$）
（↑$R_2$ に流れる電流 $I_1$ と $I_2$ は互いに逆向きなので引き算しています。）

 

ループ②の回路方程式は、次のようになります。

 

$0 = R_3 I_2 + R_2 \left( I_2 - I_1 \right)$　…（$\mathrm{B}$）
（↑電源がないループなので左辺はゼロになります。電流の符号にも注意しましょう。）

 

（$\mathrm{A}$）と（$\mathrm{B}$）の連立方程式

 

$\left\{ \begin{array}{l} V = R_1 I_1 + R_2 \left( I_1 - I_2 \right) \text{…（} \mathrm{A} \text{）} \\ 0 = R_3 I_2 + R_2 \left( I_2 - I_1 \right) \text{…（} \mathrm{B} \text{）} \end{array} \right.$

 

を電流 $I_1$ 、$I_2$ について解けば、ループ①とループ②の電流が求められます。

 

（$\mathrm{A}$）式より、

 

$V = R_1 I_1 + R_2 I_1 - R_2 I_2$　、　$V = \left( R_1 + R_2 \right) I_1 -R_2 I_2$　、　$\left( R_1 + R_2 \right) I_1 = V + R_2 I_2$

 

$\therefore I_1 = \dfrac{V +R_2 I_2}{R_1 + R_2}$　…（$\mathrm{C}$）

 

（$\mathrm{B}$）式より、

 

$\therefore 0 = R_3 I_2 + R_2 I_2 - R_2 I_1$　…（$\mathrm{D}$）

 

（$\mathrm{C}$）を（$\mathrm{D}$）式に代入すると、

 

$0 = R_3 I_2 + R_2 I_2 - R_2 \cdot \dfrac{V +R_2 I_2}{R_1 + R_2}$

 

$0 = R_3 I_2 + R_2 I_2 - \dfrac{R_2 V +{R_2}^2 I_2}{R_1 + R_2}$

 

$0 = R_3 I_2 + R_2 I_2 - \dfrac{R_2 V}{R_1 + R_2}$ $- \dfrac{{R_2}^2}{R_1 + R_2} I_2$

 

$\left( R_3 + R_2 - \dfrac{{R_2}^2}{R_1 + R_2} \right) I_2$ $= \dfrac{R_2 V}{R_1 + R_2}$

 

$\dfrac{\left( R_3 + R_2 \right) \left( R_1 + R_2 \right) - {R_2}^2}{R_1 + R_2} I_2$ $= \dfrac{R_2 V}{R_1 + R_2}$

 

$\left( R_1 R_3 + R_2 R_3 + R_1 R_2 + {R_2}^2 - {R_2}^2 \right) I_2$ $= R_2 V$

 

$\therefore I_2 = \dfrac{R_2 V}{R_1 R_2 + R_2 R_3 + R_1 R_3}$　…（$\mathrm{E}$）　（←ループ②の電流 $I_2$ の式）

 

電流 $I_2$ の式が求められたので、（$\mathrm{E}$）を（$\mathrm{C}$）式に代入して電流 $I_1$ の式を求めます。

 

$I_1$ $= \dfrac{V + R_2 \cdot \dfrac{R_2 V}{R_1 R_2 + R_2 R_3 + R_1 R_3}}{R_1 + R_2}$ $= \dfrac{\dfrac{R_1 R_2 + R_2 R_3 + R_1 R_3 +{R_2}^2}{R_1 R_2 + R_2 R_3 + R_1 R_3} V}{R_1 + R_2}$

 

$= \dfrac{\left( R_1 R_2 + R_2 R_3 + R_1 R_3 + {R_2}^2 \right) V}{\left( R_1 + R_2 \right) \left( R_1 R_2 + R_2 R_3 + R_1 R_3 \right)}$ $= \dfrac{\left\{ R_1 \left( R_2 + R_3 \right) + R_2 \left( R_2 + R_3 \right) \right\} V}{\left( R_1 + R_2 \right) \left( R_1 R_2 + R_2 R_3 + R_1 R_3 \right)}$

 

$= \dfrac{\left( R_2 + R_3 \right) \left( R_1 + R_2 \right) V}{\left( R_1 + R_2 \right) \left( R_1 R_2 + R_2 R_3 + R_1 R_3 \right)}$

 

$\therefore I_1 = \dfrac{\left( R_2 + R_3 \right) V}{R_1 R_2 + R_2 R_3 + R_1 R_3}$　…（$\mathrm{F}$）　（←ループ①の電流 $I_1$ の式）

 

したがって（$\mathrm{E}$）、（$\mathrm{F}$）より、ループ①とループ②の電流 $I_1$ 、$I_2$ は、

 

$\therefore$ ループ①の電流： $I_1 = \dfrac{\left( R_2 + R_3 \right) V}{R_1 R_2 + R_2 R_3 + R_1 R_3}$　［$ \mathrm{A} $］　…（$\mathrm{G}$）

 

$\therefore$ ループ②の電流： $I_2 = \dfrac{R_2 V}{R_1 R_2 + R_2 R_3 + R_1 R_3}$　［$ \mathrm{A} $］　…（$\mathrm{H}$）

 

となります。

 

$R_1$ に流れる電流は、ループ①に流れる電流そのままなので、

 

 

$R_2$ に流れる電流の向きを下向きを正と仮定すると、$R_2$ に流れる電流は $I_1$ から $I_2$ を引いた値になるので、

 

$R_2$ に流れる電流 $= I_1 - I_2$

 

$= \dfrac{\left( R_2 + R_3 \right) V}{R_1 R_2 + R_2 R_3 + R_1 R_3}$ $- \dfrac{R_2 V}{R_1 R_2 + R_2 R_3 + R_1 R_3}$ $= \dfrac{R_2 V + R_3 V - R_2 V}{R_1 R_2 + R_2 R_3 + R_1 R_3}$

 

 

$R_3$ に流れる電流は、ループ②に流れる電流そのままなので、

 

 

④で各素子（ $R_1$ 、$R_2$ 、$R_3$ ）に流れる電流が求められたので、求めた電流から各素子にかかる電圧を求めます。

 

$R_1$ にかかる電圧は、$R_1$ に流れる電流が（$\mathrm{I}$）式で与えられるので、

 

$R_1$ にかかる電圧 $= \dfrac{\left( R_2 + R_3 \right) V}{R_1 R_2 + R_2 R_3 + R_1 R_3} \times R_1$

 

 

$R_2$ にかかる電圧は、$R_2$ に流れる電流が（$\mathrm{J}$）式で与えられるので、

 

$R_2$ にかかる電圧 $= \dfrac{R_3 V}{R_1 R_2 + R_2 R_3 + R_1 R_3} \times R_2$

 

 

$R_3$ にかかる電圧は、$R_3$ に流れる電流が（$\mathrm{K}$）式で与えられるので、

 

$R_3$ にかかる電圧 $= \dfrac{R_2 V}{R_1 R_2 + R_2 R_3 + R_1 R_3} \times R_3$

 

 

以上（$\mathrm{I}$）〜（$\mathrm{N}$）より、$R_1$ 、$R_2$ 、$R_3$ にかかる電圧と流れる電流をループ解析で求めることができました。

 

 

このページの回路と同じ回路を、分圧の法則による直流回路の計算のページでは分圧の法則を使って、また、分流の法則による直流回路の計算のページでは分流の法則を使って計算していますので参考にしてみてください。
直流回路を解く解き方にはいろいろな計算方法があることが分かるかと思います。（もちろん計算結果はどれも同じになります。）

 

キルヒホッフの第二法則については、こちらのキルヒホッフの法則のページを参考にしてみてください。

分流の法則による直流回路の計算　←BACK

NEXT→　電圧源と電流源の等価変換

スポンサーリンク

ループ解析（基本）　関連ページ

合成抵抗の求め方（計算方法）

合成抵抗の計算は直流回路、交流回路の計算をするときの基本になります。合成抵抗の計算は複雑そうに思えますが、基本的には、抵抗が2個の場合の直列接続または並列接続の合成抵抗の求め方さえ分かっていれば、ほとんどの回路の合成抵抗を求めることができます。

短絡されている抵抗がある場合の合成抵抗の求め方

短絡されている抵抗がある場合の合成抵抗の求め方について解説しています。回路に短絡されている抵抗があるんだけど、どうやって合成抵抗を求めるの？なんてときに参考にしてみてください。

重ね合わせの理

重ね合わせの理について解説しています。重ね合わせの理は、重ね合わせの定理、重ねの理とも呼ばれ、回路に電源が複数ある場合によく使われる定理です。電圧源が2つある回路や、電圧源と電流源が混在した回路などの重ね合わせの理を使った計算方法についても解説していますので参考にしてみてください。

テブナンの定理

テブナンの定理（鳳-テブナンの定理）について解説しています。テブナンの定理は等価電圧源の定理とも呼ばれ、回路の特定の素子に流れる電流を求めるときに有用な定理です。テブナンの定理を使った回路の計算方法や、テブナンの定理の証明についても解説していますので参考にしてみてください。

ノートンの定理

ノートンの定理について解説しています。ノートンの定理は等価電流源の定理とも呼ばれ、回路の特定の素子にかかる電圧を求めるときに有用な定理です。ノートンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。

ミルマンの定理

ミルマンの定理について解説しています。ミルマンの定理は全電圧の定理とも呼ばれ、抵抗と電源の直列接続が複数並列に接続されている回路の端子電圧を求めたいときに有用な定理です。ミルマンの定理の式の導出方法や、ミルマンの定理を使った回路の計算方法などについても解説していますので参考にしてみてください。

分圧の法則による直流回路の計算

分圧の法則を使った直流回路の計算方法の例です。分圧の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。

分流の法則による直流回路の計算

分流の法則を使った直流回路の計算方法の例です。分流の法則は直流回路、交流回路どちらでも使える法則で、回路計算の基本になります。

電圧源と電流源の等価変換

電圧源と電流源の等価変換について解説しています。電圧源と電流源が等価になるための条件や、電圧源から電流源、電流源から電圧源への等価変換のやり方などについて解説していますので参考にしてみてください。

電源から供給できる最大電力（最大有能電力）

電源から供給できる最大電力（最大有能電力）について解説しています。内部抵抗をもつ電源は、負荷に供給できる電力に上限（限界）があります。電源からの供給電力が最大になるための条件や、負荷に供給できる電源の最大電力（最大有能電力）などについて解説していますので、参考にしてみてください。

コンデンサの静電容量と電荷の計算の基本（直列接続と並列接続）

コンデンサの静電容量と電荷の計算の基本についてまとめています。コンデンサの計算は、コンデンサ2個を直列接続または並列接続したときの考え方と計算方法が基本になります。

合成静電容量の求め方（計算方法）

合成静電容量の計算は直流回路、交流回路の計算をするときの基本になります。合成静電容量の計算は複雑そうに思えますが、基本的には、コンデンサが2個の場合の直列接続または並列接続の合成静電容量の求め方さえ分かっていれば、ほとんどの回路の合成静電容量を求めることができます。

ジュール熱とジュールの法則

抵抗や金属などの導体に電流が流れたときに発生するジュール熱と、ジュールの法則について解説しています。ジュール熱が発生する理由（原理）についても解説していますので、ジュール熱・ジュールの法則の勉強の参考にしてみてください。