スポンサーリンク
定電圧源
※ページ内にPR・広告が含まれる場合があります。
電源の内部抵抗が $0\,\Omega$ で、接続される負荷によらず常に一定の電圧を出力する電源(電圧源)を定電圧源(または理想電圧源)といいます。
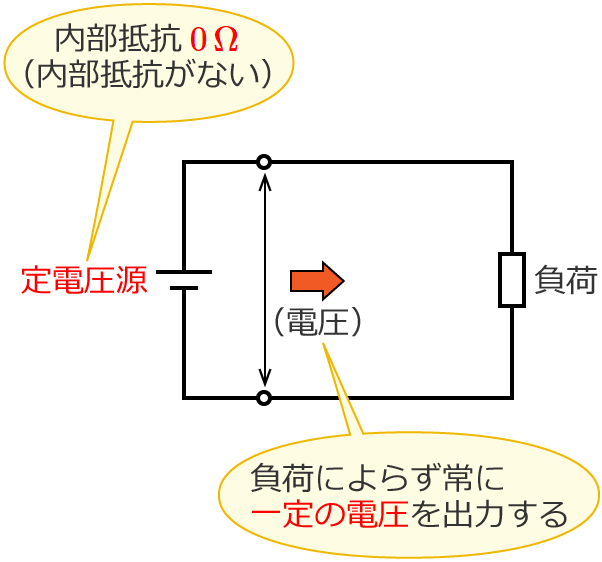
例えば次の図のように、$V$[$\mathrm{V}$]の電圧を出力する定電圧源に、可変抵抗 $R$(抵抗の大きさを変えることができる抵抗)が接続された回路があるとします。
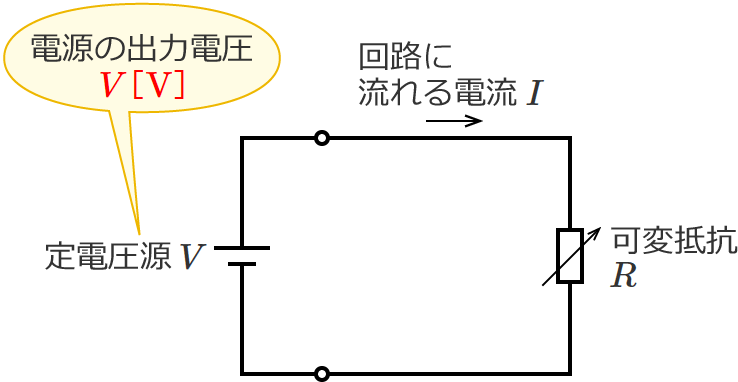
この回路において、負荷の抵抗(可変抵抗)$R$ の大きさを変化させると回路に流れる電流 $I$ の大きさも変わりますが、
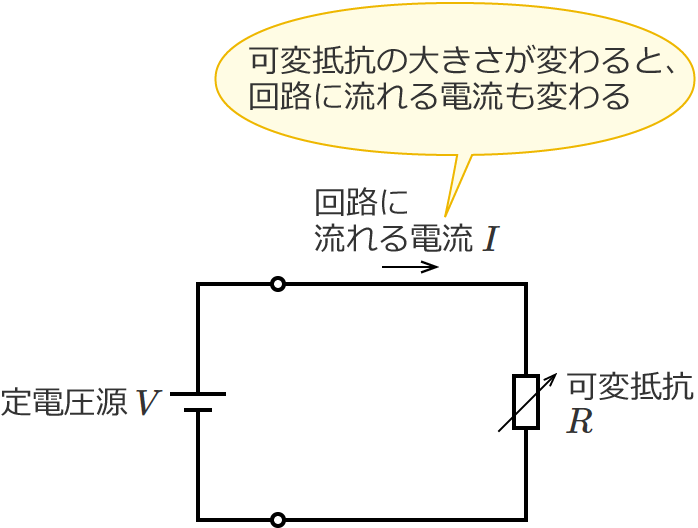
電源は定電圧源なので、回路に流れる電流 $I$ の大きさが変わっても電源から出力される電圧は常に $V$[$\mathrm{V}$]一定になります。
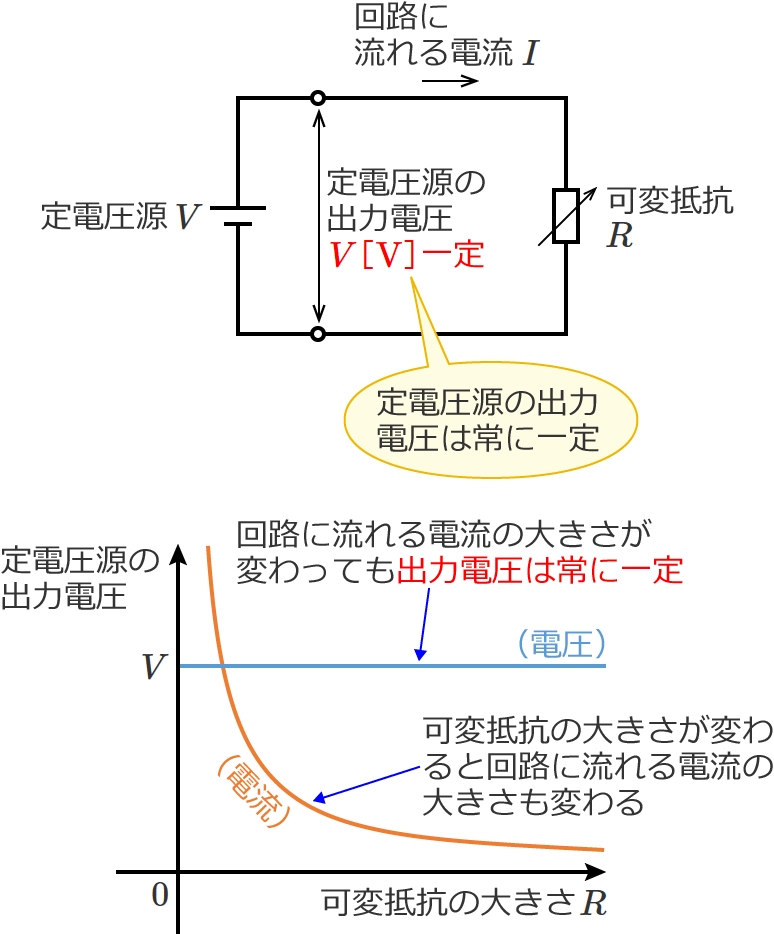
このように、負荷の抵抗の大きさや回路に流れる電流が変わっても常に一定の電圧を出力する電源が定電圧源です。
ちなみに、定電圧源を回路図に書くときは、次のような図記号が使われます。
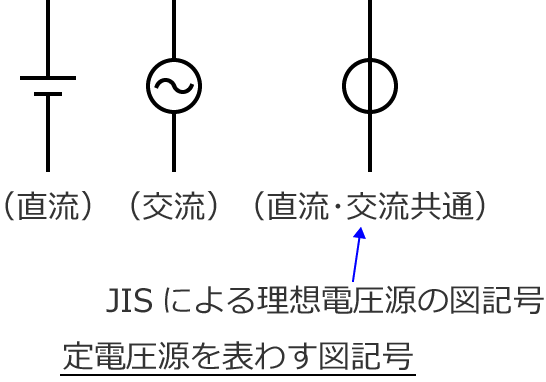
スポンサーリンク
なぜ定電圧源の出力電圧は常に一定になるのか?
例えば電池のような電源の場合、電源の内部に内部抵抗 $r$ があります。
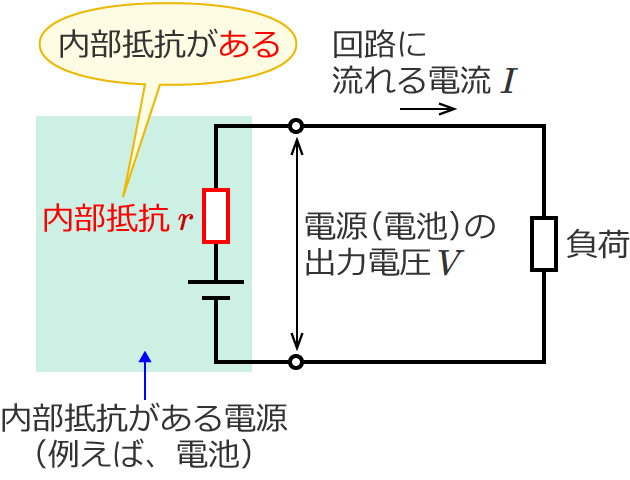
電源の内部に内部抵抗 $r$ があると、電源の内部で電圧降下が生じるため電源の出力電圧 $V$ は小さくなります。この内部抵抗 $r$ による電圧降下( $rI$ )は回路に流れる電流 $I$ が大きくなればなるほど大きくなるため、回路に流れる電流 $I$ が大きくなるほど電源の出力電圧 $V$ は小さくなっていきます。
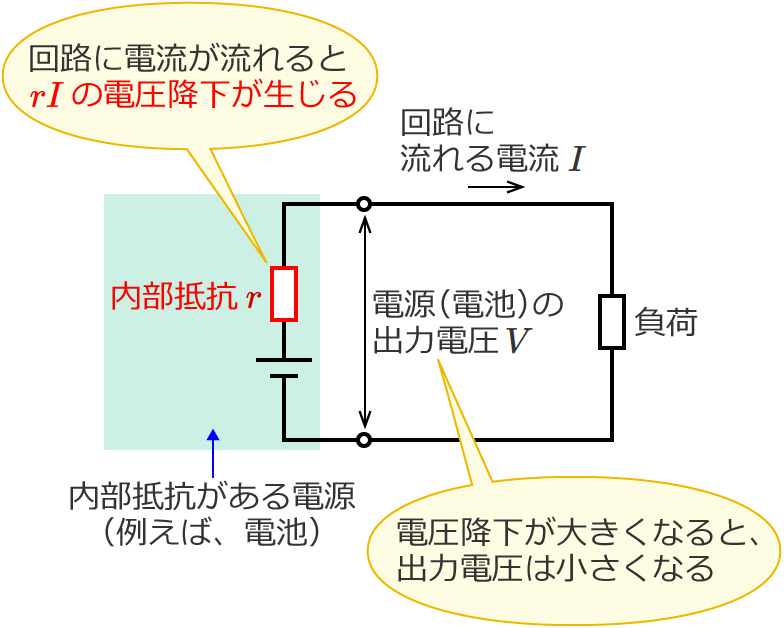
なので、内部抵抗がある電源の出力電圧は回路に流れる電流の大きさによって変わるため、内部抵抗がある電源の出力電圧は一定にはなりません。
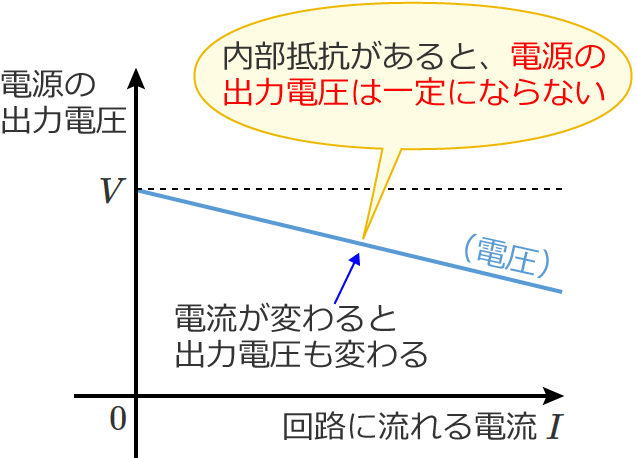
電池の内部抵抗と出力電圧(端子電圧)について詳しくは、こちらの電池の内部抵抗と端子電圧のページを参考にしてみてください。
一方、定電圧源の場合は内部抵抗 $r$ が $0\,\Omega$(=内部抵抗がない)なので、内部抵抗による電圧降下は生じません( $\because rI=0\times I=0$ )。
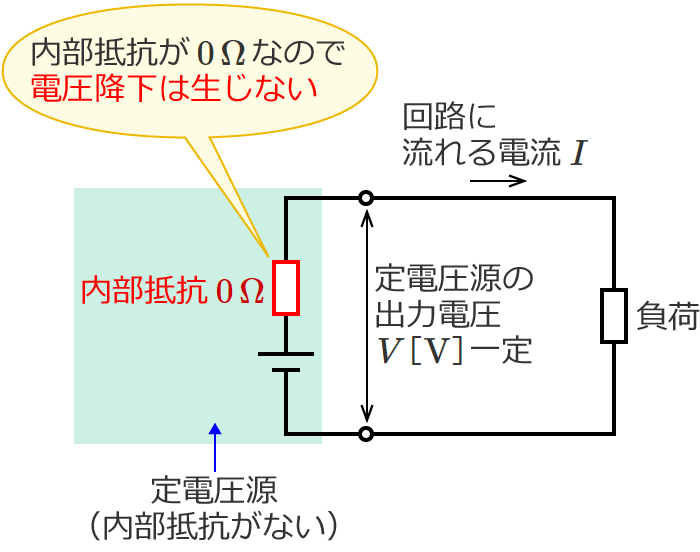
なので、定電圧源の出力電圧は一定になるんです。
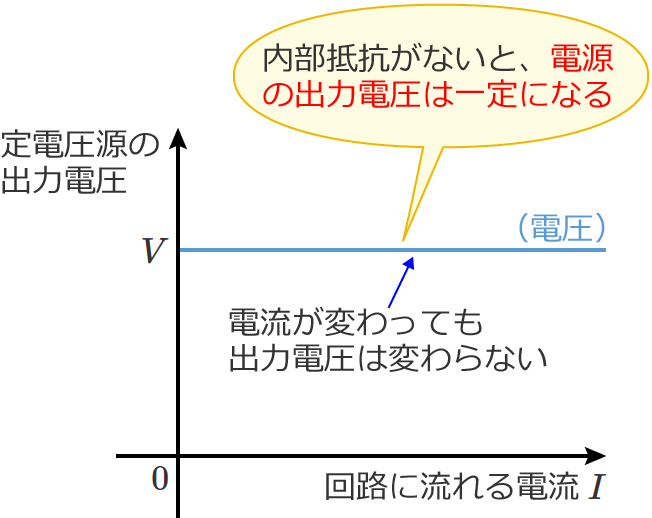
このように定電圧源は、負荷が変わっても回路に流れる電流が変わっても常に一定の電圧を出力するので、理想的な電源(電圧源)といえます。
スポンサーリンク
スポンサーリンク
定電圧源はいくらでも電流を流せる
ここまでの解説のとおり、定電圧源は、負荷が変わっても回路に流れる電流が変わっても常に一定の電圧を出力します。
ということは…。
例えば次の図のように、$10\,\mathrm{V}$ の電圧を出力する定電圧源 $V$ に $5\,\Omega$ の抵抗 $R$ が接続された回路があるとします。
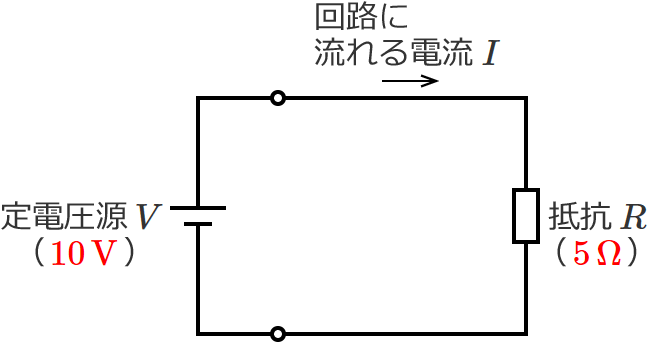
この回路に流れる電流 $I$[$\mathrm{A}$]は、オームの法則より、
$I=\dfrac{10\,\mathrm{V}}{5\,\Omega} =2\,\mathrm{A}$
$\therefore I=2\,\mathrm{A}$ (抵抗 $R$ が $5\,\Omega$ のときの回路に流れる電流 $I$ )
となり、抵抗 $R$ が $5\,\Omega$ のときは回路に流れる電流 $I$ は $2\,\mathrm{A}$ になりますね。
では、抵抗 $R$ がもっと小さいときはどうなるのでしょうか?
同じ回路で抵抗 $R$ を $0.05\,\Omega$ としてみましょう。
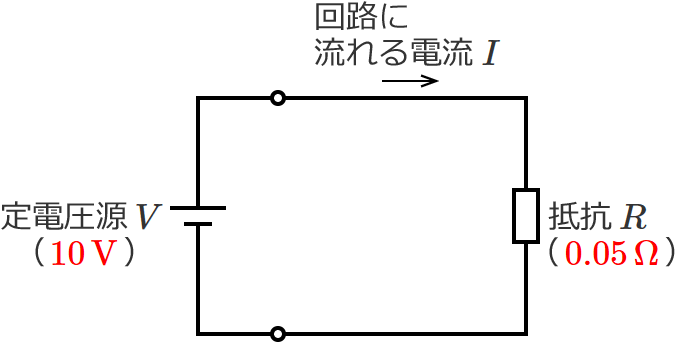
すると、回路に流れる電流 $I$ は、
$I=\dfrac{10\,\mathrm{V}}{0.05\,\Omega} =200\,\mathrm{A}$
$\therefore I=200\,\mathrm{A}$ (抵抗 $R$ が $0.05\,\Omega$ のときの回路に流れる電流 $I$ )
となり、抵抗 $R$ が $0.05\,\Omega$ のときは回路に流れる電流 $I$ は $200\,\mathrm{A}$ になります。さきほどの $5\,\Omega$ のときと比べると、なんと $100$ 倍です!
ではでは、抵抗 $R$ をもっと極端に小さくして、同じ回路で抵抗 $R$ を $0\,\Omega$ にしてみましょう。
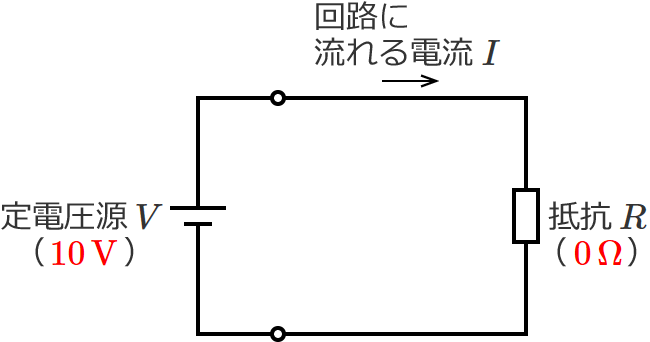
すると、回路に流れる電流 $I$ は、
$I=\dfrac{10\,\mathrm{V}}{0\,\Omega} =\infty$[$\mathrm{A}$] (定数をゼロで割ると無限大になります)
$\therefore I=\infty$[$\mathrm{A}$] (抵抗 $R$ が $0\,\Omega$ のときの回路に流れる電流 $I$ )
となり、抵抗 $R$ が $0\,\Omega$ のときは回路に流れる電流 $I$ は $\infty$(無限大)になります。
このように、定電圧源は常に一定の電圧を出力するので、負荷の抵抗の大きさを変えるといくらでも電流を流すことができるんです。(理論上)
ちなみに、抵抗 $R$ が $0\,\Omega$ というのは、定電圧源を短絡した場合に相当します。
定電圧源を短絡した場合はものすごく大きな電流(計算上は無限大の電流)が流れるので、定電圧源は短絡しないようにしなければなりません。
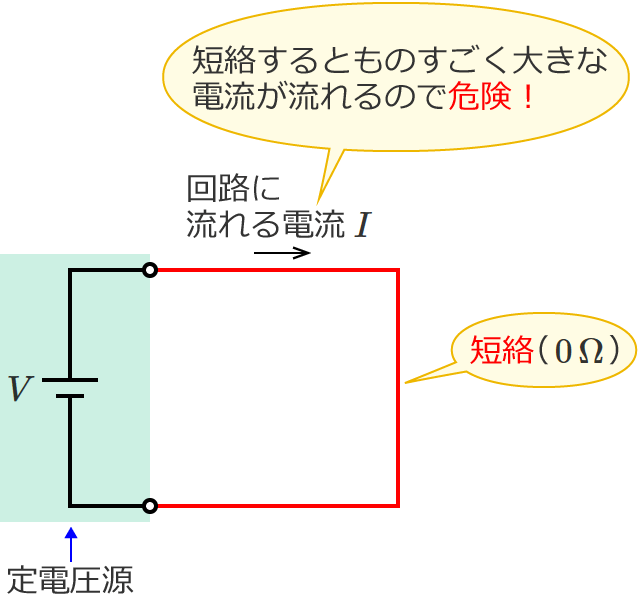
電圧源の短絡はこわいですねー、こわいですよー。
短絡について詳しくは、こちらの短絡(ショート)のページを参考にしてみてください。
- 電源の内部抵抗が $0\,\Omega$ で、接続される負荷によらず常に一定の電圧を出力する電源を定電圧源(または理想電圧源)という
- 定電圧源の内部抵抗は $0\,\Omega$ なので、内部抵抗による電圧降下は生じない(なので、一定の電圧(定電圧)を出力できる)
- 定電圧源から流れる電流は最大で無限大になる(なので、定電圧源を短絡するのは危険!)
スポンサーリンク
スポンサーリンク
定電圧源から流れる電流は最大で無限大になるので、定電圧源から取り出せる電力(=電圧×電流)も最大で無限大になります。ですが、実際の電源には内部抵抗があるため、実際の電源から取り出せる最大電力には上限があります。
実際の電源から取り出せる最大電力については、こちらの電源から供給できる最大電力(最大有能電力)のページを参考にしてみてください。
定電圧源は一定の電圧を出力する電源ですが、電圧ではなく一定の電流を出力する電源として定電流源があります。定電流源については、こちらの定電流源のページを参考にしてみてください。
スポンサーリンク
定電圧源 関連ページ
- 導体と絶縁体(不導体)
- 導体と絶縁体(不導体)について解説しています。「導体」と「絶縁体」は、電気でよく使われる用語ですので、おぼえておくようにしましょう。
- 導体の抵抗値と温度の関係
- 導体の抵抗値と温度の関係について解説しています。導体の抵抗値と温度の関係は、電気の基礎的なところですので、おぼえておくようにしましょう。
- 短絡(ショート)
- 電気回路の短絡(ショート)について解説しています。「短絡」はショートともいい、電気でよく使われる用語ですので、おぼえておくようにしましょう。
- 開放(オープン)
- 電気回路の開放(オープン)について解説しています。「開放」はオープンともいい、電気でよく使われる用語ですので、おぼえておくようにしましょう。
- 電位と電位差
- 電位と電位差について解説しています。「電位」と「電位差」は、電気でよく使われる用語ですので、おぼえておくようにしましょう。
- 定電流源
- 定電流源について解説しています。定電流源は電源の内部抵抗の大きさが無限大で、接続される負荷によらず常に一定の電流を出力する電源です。定電流源の出力電流が一定になる理由などについても解説していますので参考にしてみてください。
- 電池の内部抵抗と端子電圧
- 電池の内部抵抗と端子電圧について解説しています。電池に内部抵抗があると電池の端子電圧が起電力よりも小さくなる理由や、電池から流れる電流と端子電圧の関係などについて解説していますので、参考にしてみてください。
- SI接頭語
- SI接頭語について解説しています。SI接頭語は、アルファベットやギリシャ文字で表わされ、大きな桁の値や小さな桁の値を表わすときなどに単位記号の前に付けて用いられる接頭語です。SI接頭語の一覧表と使い方も掲載していますので参考にしてみてください。


