スポンサーリンク
SI接頭語
※ページ内にPR・広告が含まれる場合があります。
SI接頭語は、大きな桁の値や小さな桁の値を表わすときなどに、単位記号の前に付けて用いられる接頭語です。SI接頭語はアルファベットやギリシャ文字で表わされ、SI接頭語はSI接頭辞とか、単に接頭語とも呼ばれます。
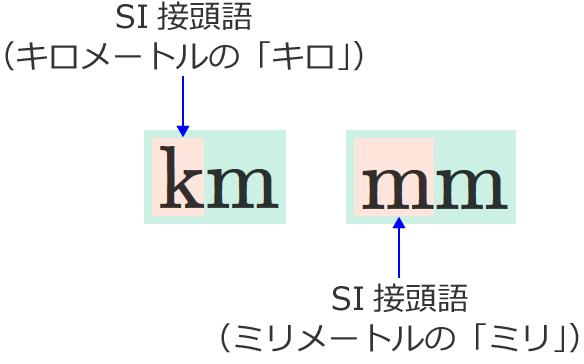
SI接頭語の例として身近なものでは、長い距離を表わすときに使う単位 $\mathrm{km}$(キロメートル)の「 $\mathrm{k}$(キロ)」や、短い長さを表わすときに使う単位 $\mathrm{mm}$(ミリメートル)の「 $\mathrm{m}$(ミリ)」などがあります。
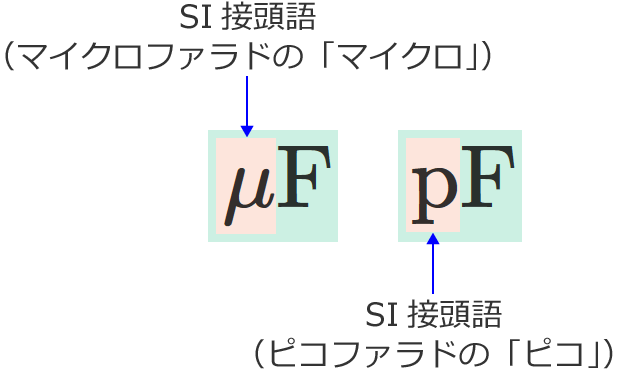
また、電気回路でよく扱われるコンデンサの静電容量の単位では、$10^{-6}$ の大きさを表わす「 $\mu$(マイクロ)」や、$10^{-12}$ の大きさを表わす「 $\mathrm{p}$(ピコ)」などのSI接頭語が使われています。
スポンサーリンク
10の整数乗倍を表わすSI接頭語
SI接頭語( $10$ の整数乗倍を表わすSI接頭語)を一覧表にまとめると、次の表のようになります。
| 接頭語 | 大きさ | ||
|---|---|---|---|
| 名称 | 記号 | ||
| ヨタ(yotta) | $\mathrm{Y}$ | $10^{24}$ | $1\, 000\, 000\, 000\, 000\, 000\, 000\, 000\, 000$ |
| ゼタ(zetta) | $\mathrm{Z}$ | $10^{21}$ | $1\, 000\, 000\, 000\, 000\, 000\, 000\, 000$ |
| エクサ(exa) | $\mathrm{E}$ | $10^{18}$ | $1\, 000\, 000\, 000\, 000\, 000\, 000$ |
| ペタ(peta) | $\mathrm{P}$ | $10^{15}$ | $1\, 000\, 000\, 000\, 000\, 000$ |
| テラ(tera) | $\mathrm{T}$ | $10^{12}$ | $1\, 000\, 000\, 000\, 000$ |
| ギガ(giga) | $\mathrm{G}$ | $10^{9}$ | $1\, 000\, 000\, 000$ |
| メガ(mega) | $\mathrm{M}$ | $10^{6}$ | $1\, 000\, 000$ |
| キロ(kilo) | $\mathrm{k}$ | $10^{3}$ | $1\, 000$ |
| ヘクト(hecto) | $\mathrm{h}$ | $10^{2}$ | $100$ |
| デカ(deca) | $\mathrm{da}$ | $10^{1}$ | $10$ |
| デシ(deci) | $\mathrm{d}$ | $10^{-1}$ | $0.1$ |
| センチ(centi) | $\mathrm{c}$ | $10^{-2}$ | $0.01$ |
| ミリ(milli) | $\mathrm{m}$ | $10^{-3}$ | $0.001$ |
| マイクロ(micro) | $\mu$ | $10^{-6}$ | $0.000\, 001$ |
| ナノ(nano) | $\mathrm{n}$ | $10^{-9}$ | $0.000\, 000\, 001$ |
| ピコ(pico) | $\mathrm{p}$ | $10^{-12}$ | $0.000\, 000\, 000\, 001$ |
| フェムト(femto) | $\mathrm{f}$ | $10^{-15}$ | $0.000\, 000\, 000\, 000\, 001$ |
| アト(atto) | $\mathrm{a}$ | $10^{-18}$ | $0.000\, 000\, 000\, 000\, 000\, 001$ |
| ゼプト(zepto) | $\mathrm{z}$ | $10^{-21}$ | $0.000\, 000\, 000\, 000\, 000\, 000\, 001$ |
| ヨクト(yocto) | $\mathrm{y}$ | $10^{-24}$ | $0.000\, 000\, 000\, 000\, 000\, 000\, 000\, 001$ |
表をみると分かるように、SI接頭語が表わす大きさは $10$ の整数乗倍になっていて、「 $\mathrm{c}$(センチ)」などの一部を除くと、その乗数は $3$ の倍数になっています。
SI接頭語の使い方の例をいくつかあげると、次のようになります。
$1\, 000\,\mathrm{m}$
⇒ $1\times$$10^{3}\,$$\mathrm{m}$
⇒ $1\,$$\mathrm{k}$$\mathrm{m}$ ($\mathrm{k}$(キロ)は $10^{3}$ を表わすSI接頭語)
$0.001\,\mathrm{m}$
⇒ $1\times$$10^{-3}\,$$\mathrm{m}$
⇒ $1\,$$\mathrm{m}$$\mathrm{m}$ ($\mathrm{m}$(ミリ)は $10^{-3}$ を表わすSI接頭語)
$4\, 000\, 000\,\Omega$
⇒ $4\times$$10^{6}\,$$\Omega$
⇒ $4\,$$\mathrm{M}$$\Omega$ ($\mathrm{M}$(メガ)は $10^{6}$ を表わすSI接頭語)
$0.000\, 020\,\mathrm{F}$
⇒ $20\times$$10^{-6}\,$$\mathrm{F}$
⇒ $20\,$$\mu$$\mathrm{F}$ ($\mu$(マイクロ)は $10^{-6}$ を表わすSI接頭語)
$2\, 100\, 000\, 000\,\mathrm{Hz}$
⇒ $2.1\times$$10^{9}\,$$\mathrm{Hz}$
⇒ $2.1\,$$\mathrm{G}$$\mathrm{Hz}$ ($\mathrm{G}$(ギガ)は $10^{9}$ を表わすSI接頭語)
$\mathrm{m}$(メートル)は長さの単位、$\Omega$(オーム)は抵抗の単位、$\mathrm{F}$(ファラド)はコンデンサの静電容量の単位、$\mathrm{Hz}$(ヘルツ)は周波数の単位です。
このように、値をSI接頭語で対応できる $10$ の整数乗倍を用いて表わし、その $10$ の整数乗倍をSI接頭語で置きかえれば、値をSI接頭語を用いて表わすことができます。
もちろん、これらは逆も成り立つので、
$1\,$$\mathrm{k}$$\mathrm{m}$ ($\mathrm{k}$(キロ)は $10^{3}$ を表わすSI接頭語)
⇒ $1\times$$10^{3}\,$$\mathrm{m}$
⇒ $1\, 000\,\mathrm{m}$
$1\,$$\mathrm{m}$$\mathrm{m}$ ($\mathrm{m}$(ミリ)は $10^{-3}$ を表わすSI接頭語)
⇒ $1\times$$10^{-3}\,$$\mathrm{m}$
⇒ $0.001\,\mathrm{m}$
$4\,$$\mathrm{M}$$\Omega$ ($\mathrm{M}$(メガ)は $10^{6}$ を表わすSI接頭語)
⇒ $4\times$$10^{6}\,$$\Omega$
⇒ $4\, 000\, 000\,\Omega$
$20\,$$\mu$$\mathrm{F}$ ($\mu$(マイクロ)は $10^{-6}$ を表わすSI接頭語)
⇒ $20\times$$10^{-6}\,$$\mathrm{F}$
⇒ $0.000\, 020\,\mathrm{F}$
$2.1\,$$\mathrm{G}$$\mathrm{Hz}$ ($\mathrm{G}$(ギガ)は $10^{9}$ を表わすSI接頭語)
⇒ $2.1\times$$10^{9}\,$$\mathrm{Hz}$
⇒ $2\, 100\, 000\, 000\,\mathrm{Hz}$
となり、SI接頭語を用いて表された値をふつうの値(SI接頭語を用いないで表わした値)で表わすこともできます。
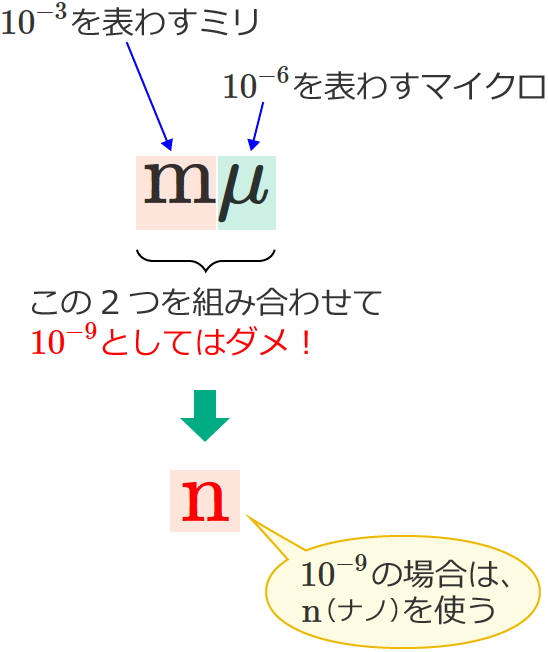
なお、SI接頭語は2つ以上の接頭語を組み合わせて使うことはできませんので、例えば、$10^{-9}$ を表わすのに $\mathrm{m}\mu$ などとしてはなりません。$10^{-9}$ の場合は $\mathrm{n}$(ナノ)を使います。
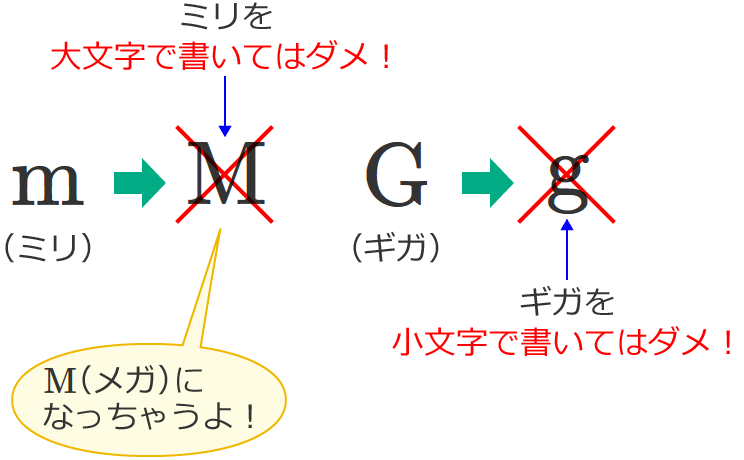
また、大文字で定められているものを小文字で書いたり、小文字で定められているものを大文字で書いたりすることはできません。SI接頭語を使うときは注意しましょう!
スポンサーリンク
スポンサーリンク
電池の内部抵抗と端子電圧 ←BACK
NEXT→ 電気のお勉強のTOP
スポンサーリンク
SI接頭語 関連ページ
- 導体と絶縁体(不導体)
- 導体と絶縁体(不導体)について解説しています。「導体」と「絶縁体」は、電気でよく使われる用語ですので、おぼえておくようにしましょう。
- 導体の抵抗値と温度の関係
- 導体の抵抗値と温度の関係について解説しています。導体の抵抗値と温度の関係は、電気の基礎的なところですので、おぼえておくようにしましょう。
- 短絡(ショート)
- 電気回路の短絡(ショート)について解説しています。「短絡」はショートともいい、電気でよく使われる用語ですので、おぼえておくようにしましょう。
- 開放(オープン)
- 電気回路の開放(オープン)について解説しています。「開放」はオープンともいい、電気でよく使われる用語ですので、おぼえておくようにしましょう。
- 電位と電位差
- 電位と電位差について解説しています。「電位」と「電位差」は、電気でよく使われる用語ですので、おぼえておくようにしましょう。
- 定電圧源
- 定電圧源について解説しています。定電圧源は電源の内部抵抗がゼロΩで、接続される負荷によらず常に一定の電圧を出力する電源です。定電圧源の出力電圧が一定になる理由などについても解説していますので参考にしてみてください。
- 定電流源
- 定電流源について解説しています。定電流源は電源の内部抵抗の大きさが無限大で、接続される負荷によらず常に一定の電流を出力する電源です。定電流源の出力電流が一定になる理由などについても解説していますので参考にしてみてください。
- 電池の内部抵抗と端子電圧
- 電池の内部抵抗と端子電圧について解説しています。電池に内部抵抗があると電池の端子電圧が起電力よりも小さくなる理由や、電池から流れる電流と端子電圧の関係などについて解説していますので、参考にしてみてください。


