スポンサーリンク
三平方の定理(ピタゴラスの定理)
※ページ内にPR・広告が含まれる場合があります。
三平方の定理は、直角三角形の辺の長さを求めるときによく使われる定理で、数学の中でもとても重要な定理の一つです。
三平方の定理を初めて習ったのは中学だったと思うのですが、三平方の定理は高校や大学の数学でも使われ、数学の中でもとても重要な定理の一つです。
このページでは、
- 三平方の定理の式(公式)
- 三平方の定理の使い方
- 三平方の定理の証明
などについて解説していますので、このページを読んで三平方の定理をおぼえましょう。
「定理」というとなんだか難しそうな感じがしますが、使ってみるとそんなに難しくはなかったりします、よ!
スポンサーリンク
三平方の定理(ピタゴラスの定理)
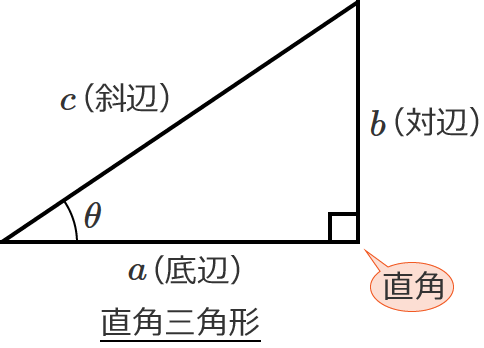
三平方の定理は、直角三角形の3つの辺の長さの関係を表わした定理で、直角三角形の直角を挟む2つの辺の長さをそれぞれ $a$ 、$b$ とし、斜辺の長さを $c$ とすると、

$a^2+b^2=c^2$ の関係が成り立つ、という定理です。
つまり、三平方の定理は、
直角三角形の直角を挟む2つの辺の長さをそれぞれ2乗して足すと、その値は斜辺の長さを2乗したものと等しくなるよ!
みたいな定理です。(みたいなというか、そういう定理。)
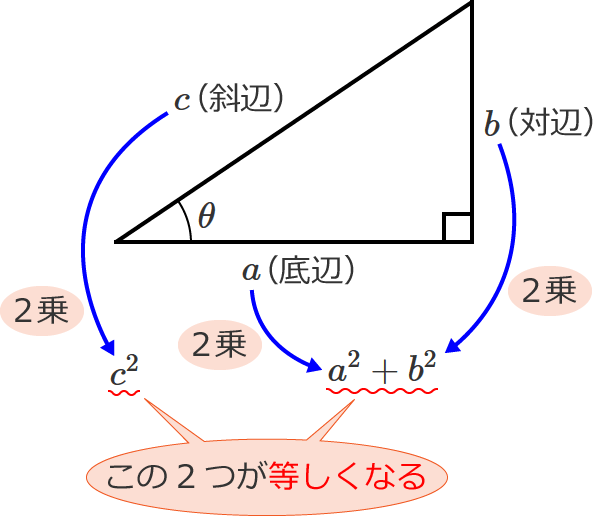
三平方の定理はピタゴラスの定理とも呼ばれ、三平方の定理の式( $a^2+b^2=c^2$ )は、直角三角形の辺の長さを求めるときによく使われています。
三平方の定理の使い方
三平方の定理の式( $a^2+b^2=c^2$ )を見ると分かるように、三平方の定理の式は3つの辺の長さ( $a$ 、$b$ 、$c$ )でできています。
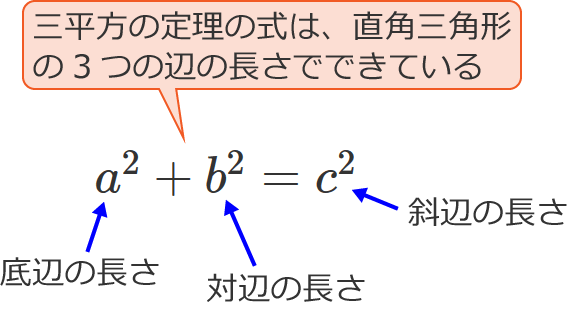
なので、直角三角形のいずれか2つの辺の長さが分かっていて、
残りの1つの辺の長さを求めたい!
なんてときには、三平方の定理の式( $a^2+b^2=c^2$ )を使うと、残りの1つの辺の長さを求めることができます。
対辺と斜辺の長さから底辺の長さを求める場合
$b$(対辺)と $c$(斜辺)の長さが分かっていて、$a$(底辺)の長さを求めたい場合は、
三平方の定理の式 $a^2+b^2=c^2$ より、 $a^2=c^2-b^2$ $\therefore a=\sqrt{c^2-b^2}$ …①
となるので、①式を使うと $a$(底辺)の長さを求めることができます。

なので、例えば、次のような $b$(対辺)の長さが $4$、$c$(斜辺)の長さが $5$ の直角三角形があるとすると、
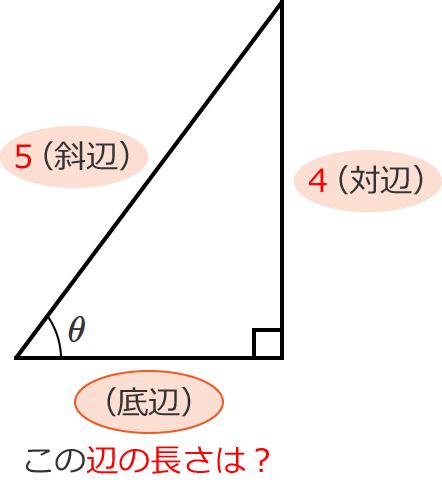
この直角三角形の $a$(底辺)の長さは、次のように計算することができます。
$a=\sqrt{c^2-b^2} =\sqrt{5^2-4^2}$ $=\sqrt{25-16}$ $=\sqrt{9} =3$
$\therefore a$(底辺)$=3$
底辺と斜辺の長さから対辺の長さを求める場合
$a$(底辺)と $c$(斜辺)の長さが分かっていて、$b$(対辺)の長さを求めたい場合は、
三平方の定理の式 $a^2+b^2=c^2$ より、 $b^2=c^2-a^2$ $\therefore b=\sqrt{c^2-a^2}$ …②
となるので、②式を使うと $b$(対辺)の長さを求めることができます。

なので、例えば、次のような $a$(底辺)の長さが $\sqrt{3}$、$c$(斜辺)の長さが $2$ の直角三角形があるとすると、
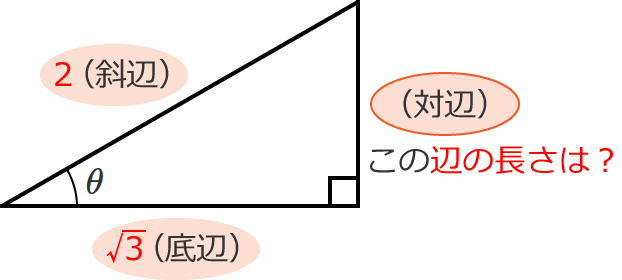
この直角三角形の $b$(対辺)の長さは、次のように計算することができます。
$b=\sqrt{c^2-a^2} =\sqrt{2^2-(\sqrt{3} )^2}$ $=\sqrt{4-3}$ $=\sqrt{1}$ $=1$
$\therefore b$(対辺)$=1$
底辺と対辺の長さから斜辺の長さを求める場合
$a$(底辺)と $b$(対辺)の長さが分かっていて、$c$(斜辺)の長さを求めたい場合は、
三平方の定理の式 $a^2+b^2=c^2$ より、 $c^2=a^2+b^2$ $\therefore c=\sqrt{a^2+b^2}$ …③
となるので、③式を使うと $c$(斜辺)の長さを求めることができます。

なので、例えば、次のような $a$(底辺)の長さが $1$、$b$(対辺)の長さが $1$ の直角三角形があるとすると、
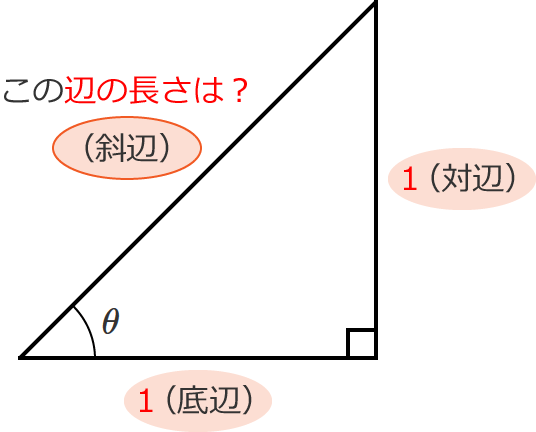
この直角三角形の $c$(斜辺)の長さは、次のように計算することができます。
$c=\sqrt{a^2+b^2} =\sqrt{1^2+1^2}$ $=\sqrt{1+1}$ $=\sqrt{2}$
$\therefore c$(斜辺)$=\sqrt{2}$
以上のように、三平方の定理の式を使うと直角三角形の辺の長さ(残り一つの辺の長さ)を求めることができるので、三平方の定理の式は、
直角三角形の辺の長さを求めるときの公式
としてよく使われています。
スポンサーリンク
スポンサーリンク
三平方の定理の証明
ここまでの解説で三平方の定理と使い方が分かったと思うので(たぶん)、ついでに、三平方の定理の証明もおぼえてしまいましょう。
三平方の定理を証明する方法は色々いっぱいあるんですが、その中でもたぶん分かりやすい(と思う)方法を紹介します。
この証明方法は、三角形と正方形の面積の求め方さえ分かっていれば理解できる証明方法ですので、証明は苦手!という方でも比較的理解しやすいと思います。
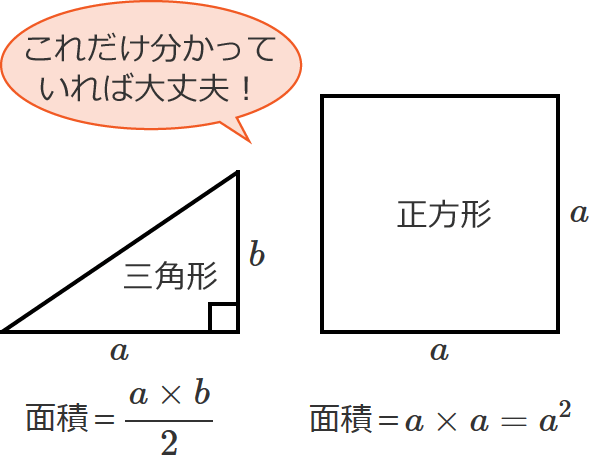
では、三平方の定理の証明をしてみます。
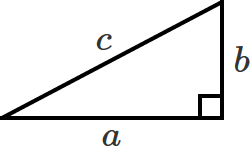
まず初めに、底辺の長さが $a$、対辺の長さが $b$、斜辺の長さが $c$ の直角三角形を書きます。
次に、いま書いた直角三角形と合同な直角三角形(同じ形で同じ大きさの直角三角形)を次のように書きます。(反時計回りに90°回転させています。)
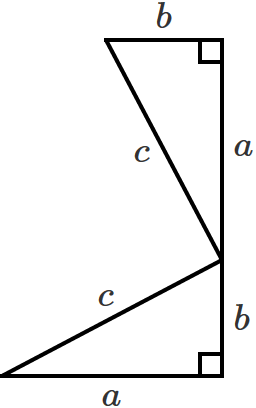
さらに反時計回りに90°回転させた直角三角形を次のように書きます。
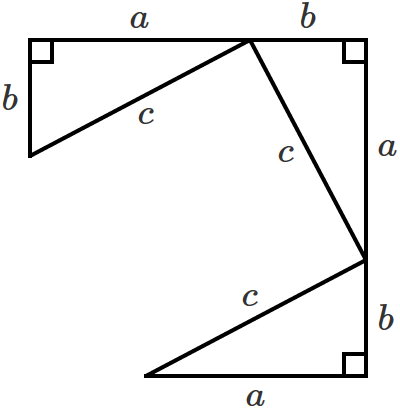
またまたさらに、反時計回りに90°回転させた直角三角形を次のように書きます。
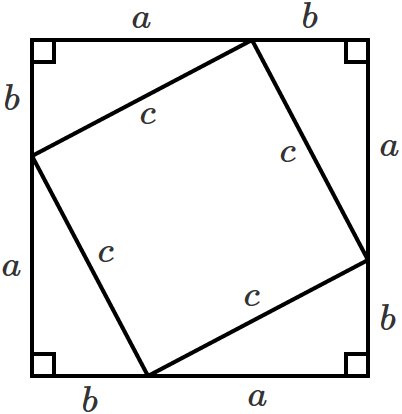
すると、「少し傾いた正方形」と「4つの直角三角形」からできている「正方形」の図形ができました。
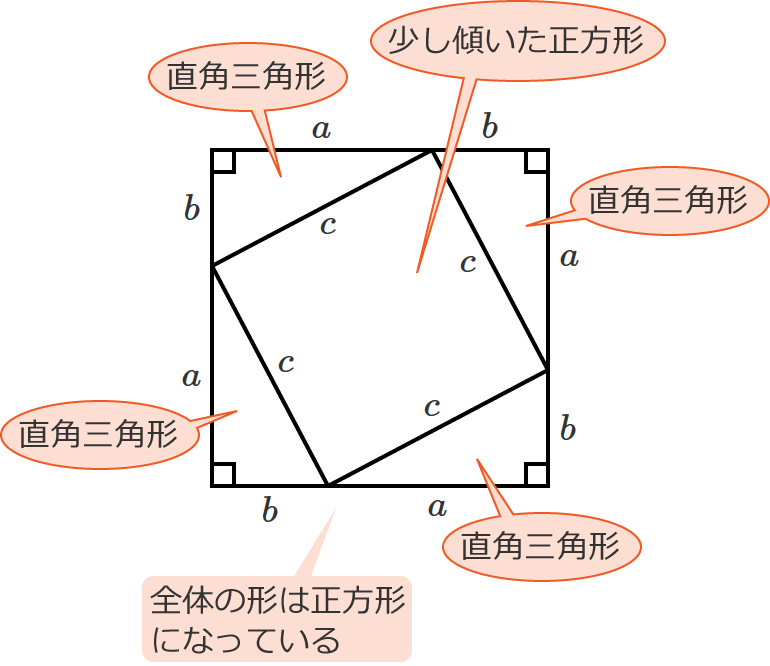
この図形全体の形は、辺の長さが $a+b$ の正方形になっているので、この正方形の面積は、
正方形の面積 $=\left( a+b\right)\times \left( a+b\right)$ $=\left( a+b\right)^2$
$\therefore$ 正方形の面積 $=\left( a+b\right)^2$ …④ になります。
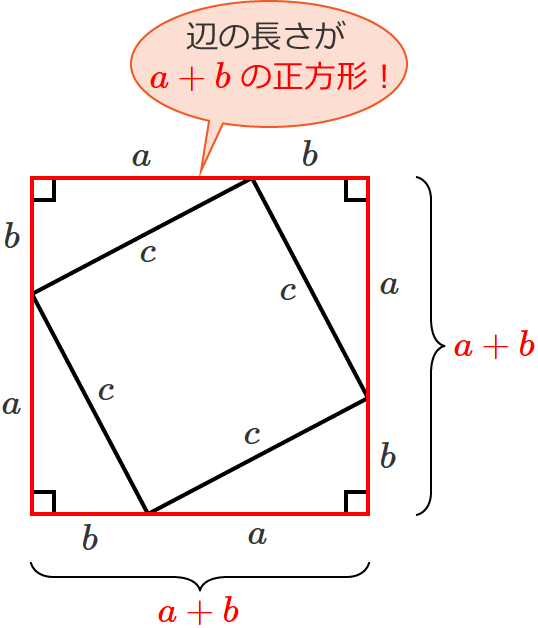
また、図形全体の正方形の面積は、「少し傾いた正方形の面積」に「4つの直角三角形の面積」を足したものでもあるので、
正方形の面積 $=c^2+4\times\dfrac{a\times b}{2}$ $=c^2+2ab$
$\therefore$ 正方形の面積 $=c^2+2ab$ …⑤ と表わすこともできます。
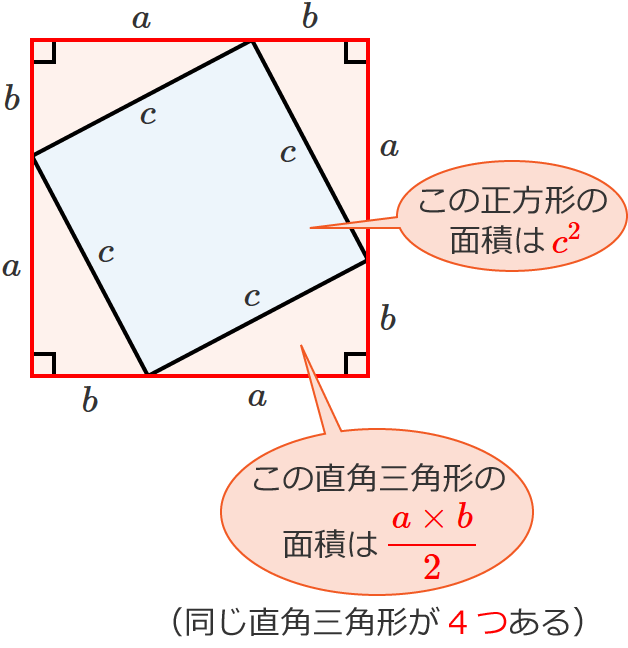
いま求めた④と⑤はどちらも図形全体の正方形の面積なので、同じものになります。なので、④=⑤とすると、
$\left( a+b\right)^2 =c^2+2ab$ の式が成り立ちます。
これを展開して整理すると、
$a^2+2ab+b^2=c^2+2ab$
$\therefore a^2+b^2=c^2$
となり、三平方の定理の式になりました!(証明終わり)
三平方の定理は色々なところで使われ、数学の基礎的なところですので、必ずおぼえておくようにしましょう。
$a^2+b^2=c^2$
スポンサーリンク
スポンサーリンク
立体の体積を求める公式 ←BACK
NEXT→ 正方形の対角線の長さの求め方
スポンサーリンク
三平方の定理(ピタゴラスの定理) 関連ページ
- 図形の面積を求める公式
- 三角形、平行四辺形、ひし形、台形、正六角形、円、扇形、楕円などの平面図形の面積を求めるときに使う公式についてまとめています。図形の面積を求めたいときや、面積の公式を忘れてしまったときなどの参考にしてみてください。
- 立体の体積を求める公式
- 直方体、三角柱、円柱、三角錐、円錐、球、中空球、楕円体などの立体の体積を求めるときに使う公式についてまとめています。立体の体積を求めたいときや、体積の公式を忘れてしまったときなどの参考にしてみてください。
- 正方形の対角線の長さの求め方
- 正方形の対角線の長さの求め方について解説しています。正方形の対角線の長さを求めるときの参考にしてみてください。
- 長方形の対角線の長さの求め方
- 長方形の対角線の長さの求め方について解説しています。長方形の対角線の長さを求めるときの参考にしてみてください。
- 平行四辺形の対角線の長さの求め方
- 平行四辺形の対角線の長さの求め方について解説しています。平行四辺形の「辺の長さ」と「高さ」が分かっている場合、平行四辺形の「辺の長さ」と「角度」が分かっている場合について解説していますので、平行四辺形の対角線の長さを求めるときの参考にしてみてください。
- ひし形の対角線の長さの求め方
- ひし形の対角線の長さの求め方について解説しています。「対角線の半分の長さを求めてそれを2倍して求める方法」、「対角線を斜辺とする直角三角形を書いて三平方の定理を使って求める方法」について解説していますので、ひし形の対角線の長さを求めるときの参考にしてみてください。
- 立方体の対角線の長さの求め方
- 立方体の対角線の長さの求め方について解説しています。立方体の対角線の長さを求めるときの参考にしてみてください。
- 直方体の対角線の長さの求め方
- 直方体の対角線の長さの求め方について解説しています。直方体の対角線の長さを求めるときの参考にしてみてください。


