スポンサーリンク
平行四辺形の対角線の長さの求め方
※ページ内にPR・広告が含まれる場合があります。
平行四辺形の「辺の長さ」と「高さ」、または「辺の長さ」と「角度」が分かっている場合、

平行四辺形の対角線の長さは、次の手順で求めることができます。
平行四辺形の対角線の長さを求める手順

長さを求めたい対角線を斜辺とする直角三角形を書く
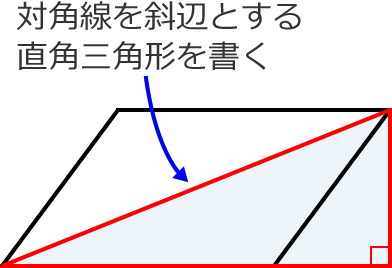
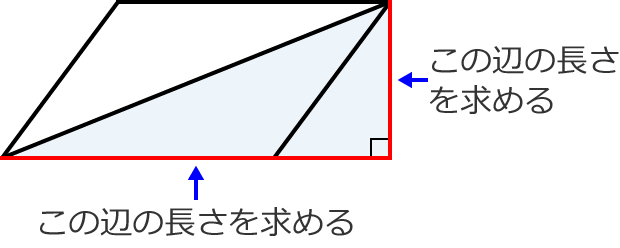
手順①で書いた直角三角形の斜辺を除く2辺それぞれの長さを求める
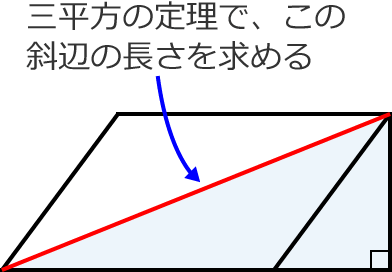
手順②で求めた2辺の長さから三平方の定理で斜辺の長さを求める(これが対角線の長さになる)
このページでは、
- 平行四辺形の「辺の長さ」と「高さ」から対角線の長さを求める場合
- 平行四辺形の「辺の長さ」と「角度」から対角線の長さを求める場合
について解説していますので、
平行四辺形の対角線の長さを求めたい!
なんてときに参考にしてみてください。
スポンサーリンク
平行四辺形の「辺の長さ」と「高さ」から対角線の長さを求める
次のように、辺の長さと高さが分かっている平行四辺形 $\mathrm{ABCD}$ があるとします。
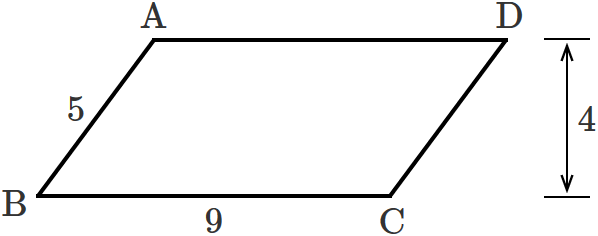
この平行四辺形の「対角線 $\mathrm{BD}$ の長さ」と「対角線 $\mathrm{AC}$ の長さ」を、先ほどの手順に従って求めてみます。
対角線BDの長さの求め方
手順①:対角線を斜辺とする直角三角形を書く
対角線 $\mathrm{BD}$ を斜辺とする直角三角形を書くと次のようになります。(直角三角形の直角になっているところの頂点は $\mathrm{E}$ とします。)
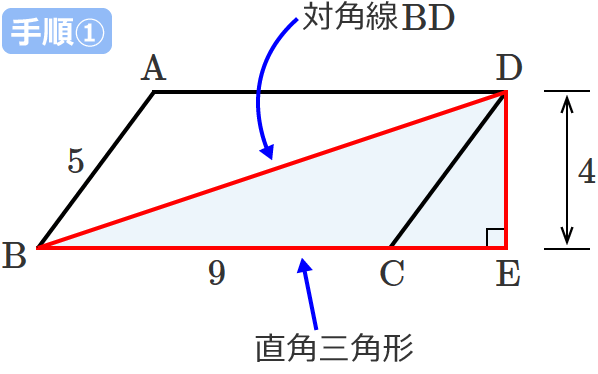
手順②:直角三角形の斜辺を除く2辺それぞれの長さを求める
直角三角形 $\mathrm{BDE}$ の辺 $\mathrm{DE}$ の長さは、平行四辺形の高さと等しいので、
$\therefore \mathrm{DE} =4$ …① となります。
また、直角三角形 $\mathrm{BDE}$ の辺 $\mathrm{BE}$ の長さは、$\mathrm{BC}$ の長さと $\mathrm{CE}$ の長さを足したものなので、$\mathrm{BE} =\mathrm{BC} +\mathrm{CE}$ となります。
ここで、$\mathrm{BC}$ の長さは平行四辺形の辺の長さなので「$9$」と分かりますが、$\mathrm{CE}$ の長さは分かりません。なので、$\mathrm{CE}$ の長さを三平方の定理を使って求めると、
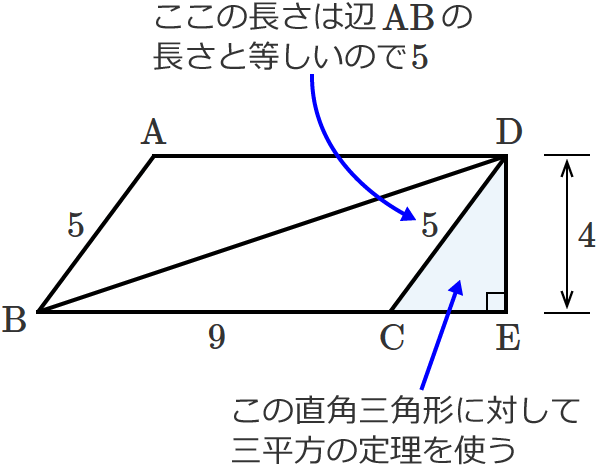
$\mathrm{CE} =\sqrt{5^2-4^2} =\sqrt{25-16}$ $=\sqrt{9}$ $=3$
$\therefore\mathrm{CE} =3$ となります。
したがって、
$\mathrm{BE} =\mathrm{BC} +\mathrm{CE} =9+3=12$
$\therefore\mathrm{BE} =12$ …② となるので、
直角三角形 $\mathrm{BDE}$ の斜辺を除く2辺( $\mathrm{DE}$ と $\mathrm{BE}$ )それぞれの長さは、①、②より、「$4$」と「$12$」になります。
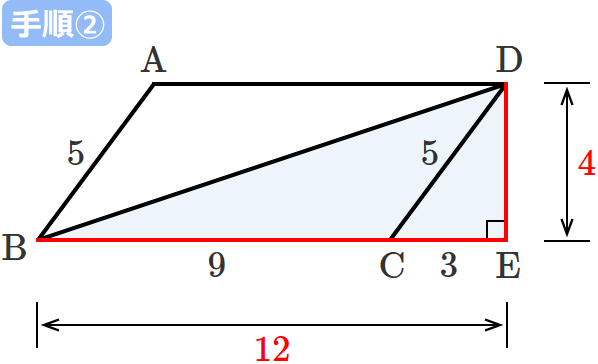
手順③:三平方の定理で斜辺の長さを求める
手順②より2辺の長さが求められたので、あとは三平方の定理で直角三角形 $\mathrm{BDE}$ の斜辺の長さを求めるだけです。
三平方の定理より、直角三角形 $\mathrm{BDE}$ の斜辺 $\mathrm{BD}$ の長さは、
$\mathrm{BD} =\sqrt{4^2+12^2} =\sqrt{16+144}$ $=\sqrt{160}$ $=4\sqrt{10}$
したがって、平行四辺形 $\mathrm{ABCD}$ の対角線 $\mathrm{BD}$ の長さは、
$\therefore\mathrm{BD} =4\sqrt{10}$
となります。
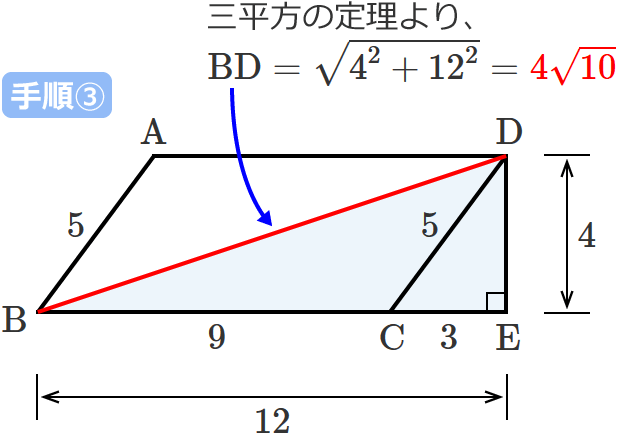
対角線ACの長さの求め方
手順①:対角線を斜辺とする直角三角形を書く
対角線 $\mathrm{AC}$ を斜辺とする直角三角形を書くと次のようになります。(直角三角形の直角になっているところの頂点は $\mathrm{F}$ とします。)
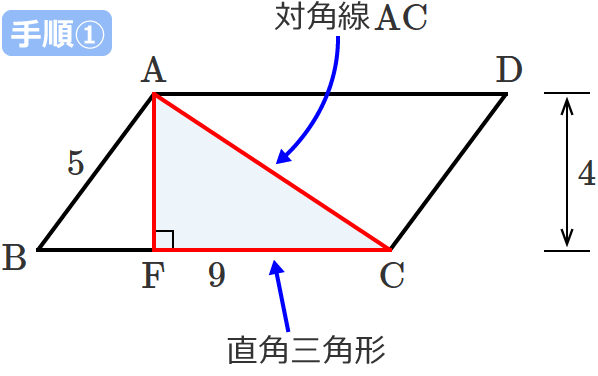
手順②:直角三角形の斜辺を除く2辺それぞれの長さを求める
直角三角形 $\mathrm{ACF}$ の辺 $\mathrm{AF}$ の長さは、平行四辺形の高さと等しいので(てか、$\mathrm{AF}$ は平行四辺形の高さ)、
$\therefore\mathrm{AF} =4$ …③ となります。
また、直角三角形 $\mathrm{ACF}$ の辺 $\mathrm{CF}$ の長さは、$\mathrm{BC}$ の長さから $\mathrm{BF}$ の長さを引いたものなので、$\mathrm{CF} =\mathrm{BC} -\mathrm{BF}$ となります。
ここで、$\mathrm{BC}$ の長さは平行四辺形の辺の長さなので「$9$」と分かりますが、$\mathrm{BF}$ の長さは分かりません。なので、$\mathrm{BF}$ の長さを三平方の定理を使って求めると、
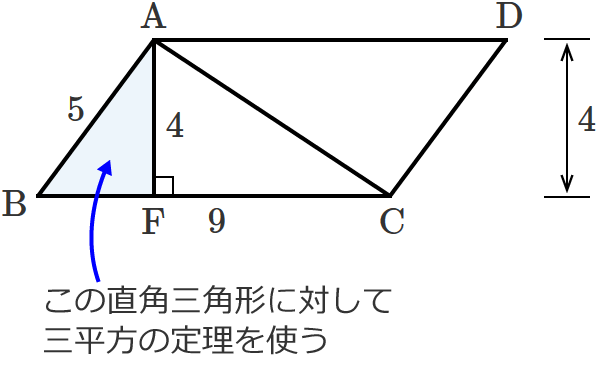
$\mathrm{BF} =\sqrt{5^2-4^2} =\sqrt{25-16}$ $=\sqrt{9}$ $=3$
$\therefore\mathrm{BF} =3$ となります。
したがって、
$\mathrm{CF} =\mathrm{BC} -\mathrm{BF} =9-3=6$
$\therefore\mathrm{CF} =6$ …④ となるので、
直角三角形 $\mathrm{ACF}$ の斜辺を除く2辺( $\mathrm{AF}$ と $\mathrm{CF}$ )それぞれの長さは、③、④より、「$4$」と「$6$」になります。
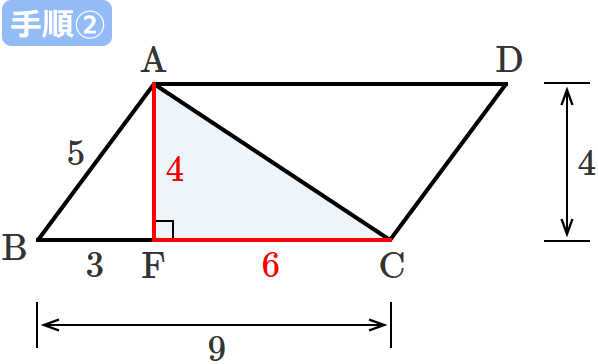
手順③:三平方の定理で斜辺の長さを求める
手順②より2辺の長さが求められたので、あとは三平方の定理で直角三角形 $\mathrm{ACF}$ の斜辺の長さを求めるだけです。
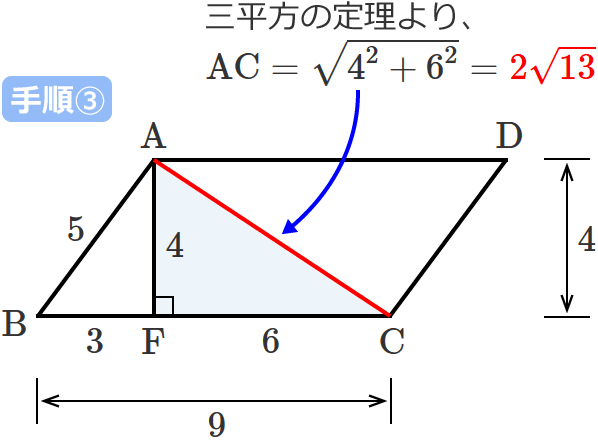
三平方の定理より、直角三角形 $\mathrm{ACF}$ の斜辺 $\mathrm{AC}$ の長さは、
$\mathrm{AC} =\sqrt{4^2+6^2} =\sqrt{16+36}$ $=\sqrt{52}$ $=2\sqrt{13}$
したがって、平行四辺形 $\mathrm{ABCD}$ の対角線 $\mathrm{AC}$ の長さは、
$\therefore\mathrm{AC} =2\sqrt{13}$
となります。
スポンサーリンク
スポンサーリンク
平行四辺形の「辺の長さ」と「角度」から対角線の長さを求める
次のように、辺の長さと角度が分かっている平行四辺形 $\mathrm{ABCD}$ があるとします。
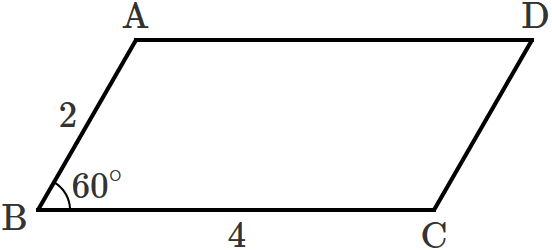
この平行四辺形の「対角線 $\mathrm{BD}$ の長さ」と「対角線 $\mathrm{AC}$ の長さ」を求めてみます。
対角線BDの長さの求め方
手順①:対角線を斜辺とする直角三角形を書く
対角線 $\mathrm{BD}$ を斜辺とする直角三角形を書くと次のようになります。(直角三角形の直角になっているところの頂点は $\mathrm{E}$ とします。)
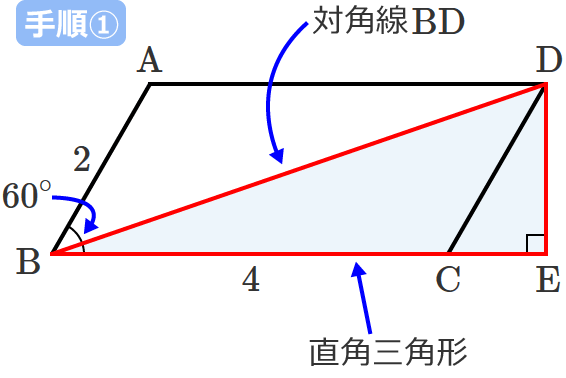
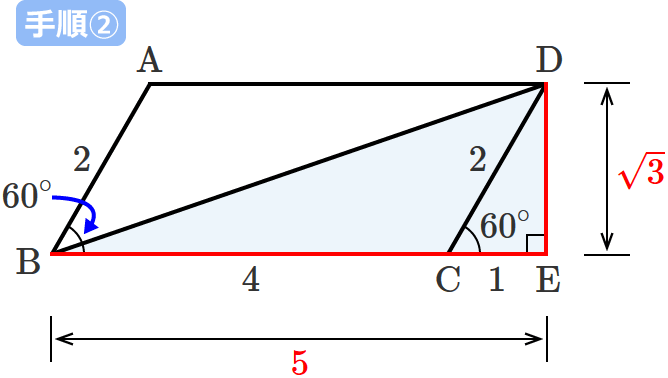
手順②:直角三角形の斜辺を除く2辺それぞれの長さを求める
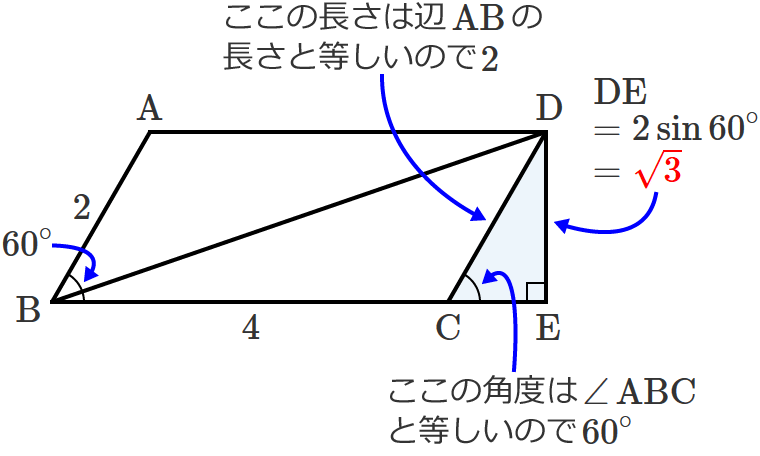
直角三角形 $\mathrm{BDE}$ の辺 $\mathrm{DE}$ の長さは、$\mathrm{DC} =2$ 、$\angle\,\mathrm{DCE} =60^\circ$ なので、
$\mathrm{DE} =\mathrm{DC}\times\sin 60^\circ =2\times\dfrac{\sqrt{3}}{2}$ $=\sqrt{3}$
$\therefore\mathrm{DE} =\sqrt{3}$ …⑤ となります。
また、直角三角形 $\mathrm{BDE}$ の辺 $\mathrm{BE}$ の長さは、$\mathrm{BC}$ の長さと $\mathrm{CE}$ の長さを足したものなので、$\mathrm{BE} =\mathrm{BC} +\mathrm{CE}$ となります。
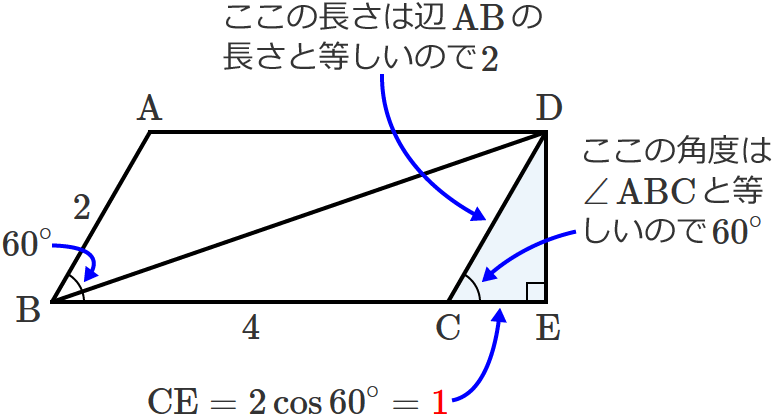
ここで、$\mathrm{BC}$ の長さは平行四辺形の辺の長さなので「$4$」と分かりますが、$\mathrm{CE}$ の長さは分かりません。なので、$\mathrm{CE}$ の長さを求めると、
$\mathrm{DC} =2$ 、$\angle\,\mathrm{DCE} =60^\circ$ より、
$\mathrm{CE} =\mathrm{DC}\times\cos 60^\circ =2\times\dfrac{1}{2} =1$
$\therefore\mathrm{CE} =1$ となります。
したがって、
$\mathrm{BE} =\mathrm{BC} +\mathrm{CE} =4+1=5$
$\therefore\mathrm{BE} =5$ …⑥ となるので、
直角三角形 $\mathrm{BDE}$ の斜辺を除く2辺( $\mathrm{DE}$ と $\mathrm{BE}$ )それぞれの長さは、⑤、⑥より、「$\sqrt{3}$」と「$5$」になります。
手順③:三平方の定理で斜辺の長さを求める
手順②より2辺の長さが求められたので、あとは三平方の定理で直角三角形 $\mathrm{BDE}$ の斜辺の長さを求めるだけです。
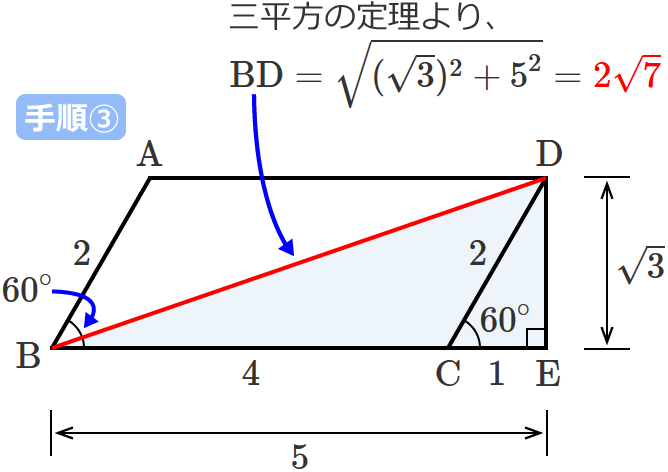
三平方の定理より、直角三角形 $\mathrm{BDE}$ の斜辺 $\mathrm{BD}$ の長さは、
$\mathrm{BD} =\sqrt{(\sqrt{3} )^2 +5^2} =\sqrt{3+25}$ $=\sqrt{28}$ $=2\sqrt{7}$
したがって、平行四辺形 $\mathrm{ABCD}$ の対角線 $\mathrm{BD}$ の長さは、
$\therefore\mathrm{BD} =2\sqrt{7}$
となります。
対角線ACの長さの求め方
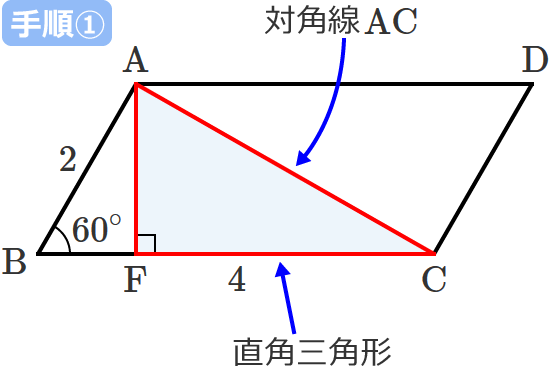
手順①:対角線を斜辺とする直角三角形を書く
対角線 $\mathrm{AC}$ を斜辺とする直角三角形を書くと次のようになります。(直角三角形の直角になっているところの頂点は $\mathrm{F}$ とします。)
手順②:直角三角形の斜辺を除く2辺それぞれの長さを求める
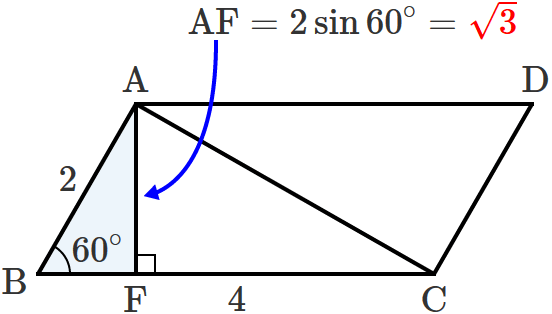
直角三角形 $\mathrm{ACF}$ の辺 $\mathrm{AF}$ の長さは、$\mathrm{AB} =2$ 、$\angle\,\mathrm{ABF} =60^\circ$ なので、
$\mathrm{AF} =\mathrm{AB}\times\sin 60^\circ =2\times\dfrac{\sqrt{3}}{2}$ $=\sqrt{3}$
$\therefore\mathrm{AF} =\sqrt{3}$ …⑦ となります。
また、直角三角形 $\mathrm{ACF}$ の辺 $\mathrm{CF}$ の長さは、$\mathrm{BC}$ の長さから $\mathrm{BF}$ の長さを引いたものなので、$\mathrm{CF} =\mathrm{BC} -\mathrm{BF}$ となります。
ここで、$\mathrm{BC}$ の長さは平行四辺形の辺の長さなので「$4$」と分かりますが、$\mathrm{BF}$ の長さは分かりません。なので、$\mathrm{BF}$ の長さを求めると、
$\mathrm{AB} =2$ 、$\angle\,\mathrm{ABF} =60^\circ$ より、
$\mathrm{BF} =\mathrm{AB}\times\cos 60^\circ =2\times\dfrac{1}{2} =1$
$\therefore\mathrm{BF} =1$ となります。
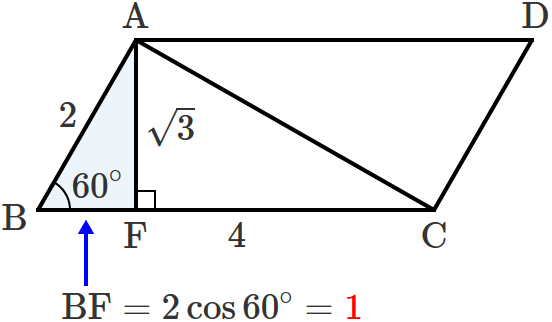
したがって、
$\mathrm{CF} =\mathrm{BC} -\mathrm{BF} =4-1=3$
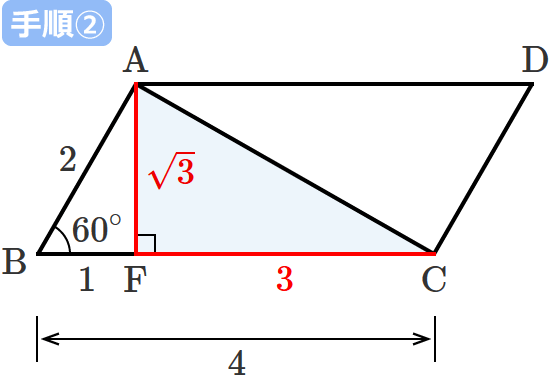
$\therefore\mathrm{CF} =3$ …⑧ となるので、
直角三角形 $\mathrm{ACF}$ の斜辺を除く2辺( $\mathrm{AF}$ と $\mathrm{CF}$ )それぞれの長さは、⑦、⑧より、「$\sqrt{3}$」と「$3$」になります。
手順③:三平方の定理で斜辺の長さを求める
手順②より2辺の長さが求められたので、あとは三平方の定理で直角三角形 $\mathrm{ACF}$ の斜辺の長さを求めるだけです。
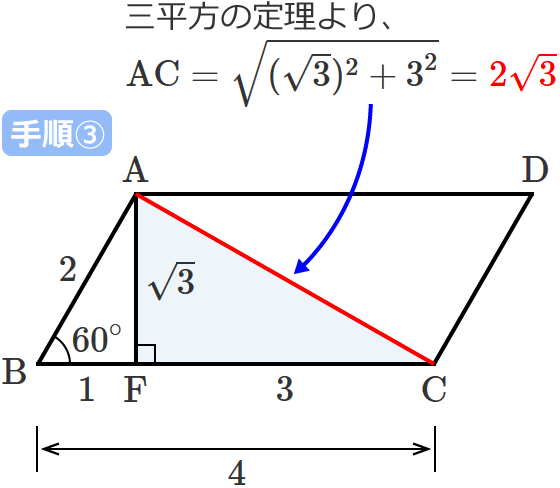
三平方の定理より、直角三角形 $\mathrm{ACF}$ の斜辺 $\mathrm{AC}$ の長さは、
$\mathrm{AC} =\sqrt{(\sqrt{3} )^2 +3^2} =\sqrt{3+9}$ $=\sqrt{12}$ $=2\sqrt{3}$
したがって、平行四辺形 $\mathrm{ABCD}$ の対角線 $\mathrm{AC}$ の長さは、
$\therefore\mathrm{AC} =2\sqrt{3}$
となります。
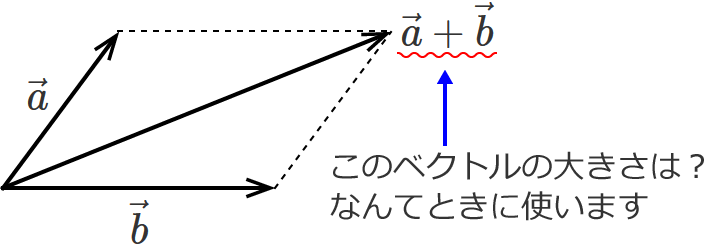
平行四辺形の対角線の長さの求め方の解説は以上になりますが、ここで解説した対角線の長さの求め方は、例えば、2つのベクトルを合成したベクトルの大きさを求めるときなどにもよく使うので、おぼえておくようにしましょう。
- 対角線を斜辺とした直角三角形を書いて、三平方の定理を使って対角線(斜辺)の長さを求める
スポンサーリンク
スポンサーリンク
直角三角形の辺の長さを求めるときに使っている三平方の定理についてもうちょっと詳しく知りたい方は、こちらの三平方の定理(ピタゴラスの定理)のページを参考にしてみてください。
また、$\sin$ 、$\cos$ については、こちらの三角関数のsin、cos、tanって何?のページを参考にしてみてください。
長方形の対角線の長さの求め方 ←BACK
NEXT→ ひし形の対角線の長さの求め方
スポンサーリンク
平行四辺形の対角線の長さの求め方 関連ページ
- 図形の面積を求める公式
- 三角形、平行四辺形、ひし形、台形、正六角形、円、扇形、楕円などの平面図形の面積を求めるときに使う公式についてまとめています。図形の面積を求めたいときや、面積の公式を忘れてしまったときなどの参考にしてみてください。
- 立体の体積を求める公式
- 直方体、三角柱、円柱、三角錐、円錐、球、中空球、楕円体などの立体の体積を求めるときに使う公式についてまとめています。立体の体積を求めたいときや、体積の公式を忘れてしまったときなどの参考にしてみてください。
- 三平方の定理(ピタゴラスの定理)
- 三平方の定理(ピタゴラスの定理)について解説しています。三平方の定理の式(公式)、使い方、証明などについて解説していますので、三平方の定理の勉強の参考にしてみてください。
- 正方形の対角線の長さの求め方
- 正方形の対角線の長さの求め方について解説しています。正方形の対角線の長さを求めるときの参考にしてみてください。
- 長方形の対角線の長さの求め方
- 長方形の対角線の長さの求め方について解説しています。長方形の対角線の長さを求めるときの参考にしてみてください。
- ひし形の対角線の長さの求め方
- ひし形の対角線の長さの求め方について解説しています。「対角線の半分の長さを求めてそれを2倍して求める方法」、「対角線を斜辺とする直角三角形を書いて三平方の定理を使って求める方法」について解説していますので、ひし形の対角線の長さを求めるときの参考にしてみてください。
- 立方体の対角線の長さの求め方
- 立方体の対角線の長さの求め方について解説しています。立方体の対角線の長さを求めるときの参考にしてみてください。
- 直方体の対角線の長さの求め方
- 直方体の対角線の長さの求め方について解説しています。直方体の対角線の長さを求めるときの参考にしてみてください。


