電気のお勉強｜電気機器｜誘導電動機のL形等価回路

スポンサーリンク

等価回路

三相誘導電動機の一相分のL形等価回路（簡易等価回路）は、次のように表わされます。

 

 

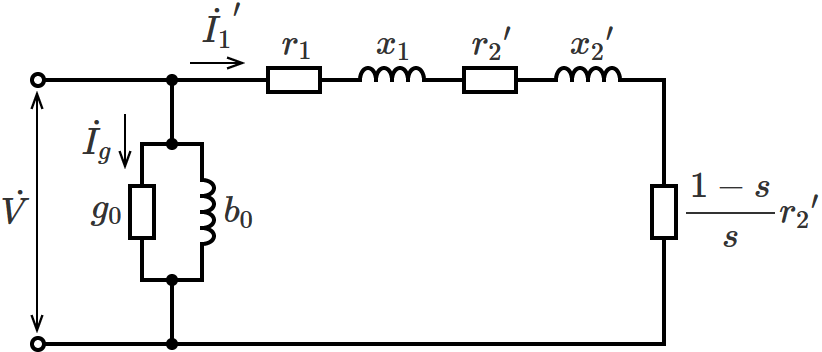
$\dot{V}$ ：一次相電圧 ［$ \mathrm{V} $］
$\dot{I_g}$ ：励磁コンダクタンスに流れる電流 ［$ \mathrm{A} $］
$g_0$ ：励磁コンダクタンス ［$ \mathrm{S} $］
$b_0$ ：励磁サセプタンス ［$ \mathrm{S} $］
$\dot{I_1}^\prime$ ：一次負荷電流 ［$ \mathrm{A} $］
$r_1$ ：一次抵抗 ［$ \Omega $］
$x_1$ ：一次漏れリアクタンス ［$ \Omega $］
${r_2}^\prime$ ：二次抵抗（一次換算値）［$ \Omega $］
${x_2}^\prime$ ：二次漏れリアクタンス（一次換算値）［$ \Omega $］
$s$ ：すべり

 

スポンサーリンク

 

励磁コンダクタンスg0に流れる電流Igの求め方

等価回路図より、励磁コンダクタンス $g_0$ には電圧 $V$ がかかっているので、励磁コンダクタンス $g_0$ に流れる電流 $I_g$ は、

 

$I_g = \left| \dot{I_g} \right| = g_0 V$

 

 

となります。

 

一次負荷電流I1’の求め方

一次負荷電流 ${I_1}^\prime$ が流れるループのインピーダンスを $\dot{Z_1}$ とすると、

 

 

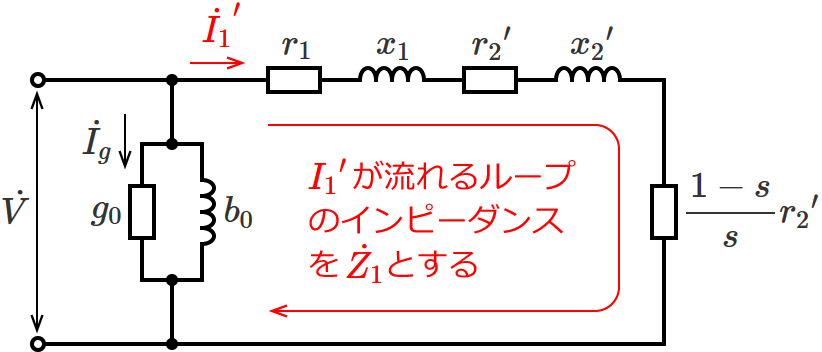
$\dot{Z_1}$ $= r_1 + j x_1 + {r_2}^\prime + j {x_2}^\prime + \dfrac{1-s}{s} {r_2}^\prime$ $= \left( r_1 + {r_2}^\prime + \dfrac{1-s}{s} {r_2}^\prime \right)$ $+ j ( x_1 + {x_2}^\prime )$ $= \left( r_1 + \left( \dfrac{s+1-s}{s} \right) {r_2}^\prime \right)$ $+ j (x_1 + {x_2}^\prime )$ $= \left( r_1 + \dfrac{{r_2}^\prime}{s} \right) + j (x_1 + {x_2}^\prime )$

 

$\therefore \dot{Z_1} = \left( r_1 + \dfrac{{r_2}^\prime}{s} \right) + j (x_1 + {x_2}^\prime )$　となるので、インピーダンス $\dot{Z_1}$ の大きさ $\left| \dot{Z_1} \right|$ は次のようになります。

 

$\therefore \left| \dot{Z_1} \right|$ $= \sqrt{\left( r_1 + \dfrac{{r_2}^\prime}{s} \right)^2 + (x_1 + {x_2}^\prime )^2}$

 

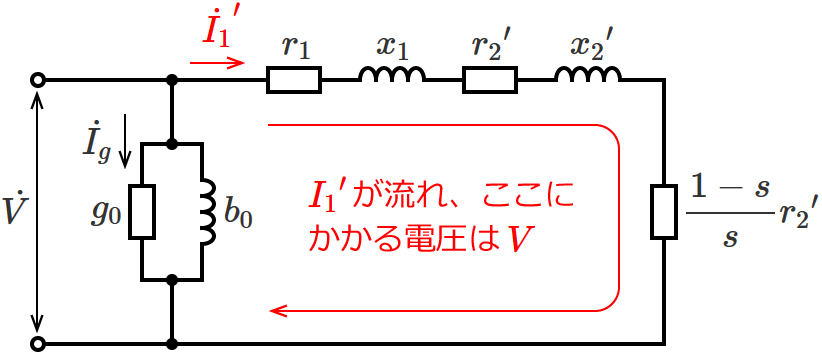
したがって、一次負荷電流 ${I_1}^\prime$ が流れるループには電圧 $V$ がかかっているので、一次負荷電流 ${I_1}^\prime$ は次のようになります。

 

${I_1}^\prime = \left| \dot{I_1}^\prime \right| = \dfrac{V}{\left| \dot{Z_1} \right|}$ $= \dfrac{V}{\sqrt{\left( r_1 + \dfrac{{r_2}^\prime}{s} \right)^2 + (x_1 + {x_2}^\prime )^2}}$

 

 

 

三相分の鉄損Piの求め方

鉄損は等価回路中の励磁コンダクタンス $g_0$ による損失であるので、一相分の鉄損を ${P_i}^\prime$ とすると ${P_i}^\prime$ は次式となります。

 

${P_i}^\prime = {I_g}^2 \dfrac{1}{g_0}$

 

ここで、励磁コンダクタンス $g_0$ に流れる電流 $I_g$ は、$I_g = g_0 V$ であるので、一相分の鉄損 ${P_i}^\prime$ は、

 

${P_i}^\prime = {I_g}^2 \dfrac{1}{g_0} = \left( g_0 V \right)^2 \cdot \dfrac{1}{g_0}$ $= {g_0}^2 \, V^2 \cdot \dfrac{1}{g_0}$ $= g_0 V^2$　となります。

 

したがって、三相分の鉄損 $P_i$ は一相分の鉄損 ${P_i}^\prime$ の3倍なので、

 

$P_i = 3 \times {P_i}^\prime = 3 \times g_0 V^2 = 3 g_0 V^2$

 

 

となります。

 

 

三相分の一次銅損PC1の求め方

一次銅損は一次抵抗 $r_1$ による損失であるので、一相分の一次銅損を ${P_{C1}}^\prime$ とすると ${P_{C1}}^\prime$ は次式となります。

 

${P_{C1}}^\prime = {{I_1}^\prime}^2 \, r_1$

 

したがって、三相分の一次銅損 $P_{C1}$ は一相分の一次銅損 ${P_{C1}}^\prime$ の3倍なので、

 

$P_{C1} = 3 \times {P_{C1}}^\prime = 3 {{I_1}^\prime}^2 \, r_1$

 

 

となります。

 

ここで、先ほど求めた一次負荷電流 ${I_1}^\prime$ を上式に代入すると、三相分の一次銅損 $P_{C1}$ は次式でも表わせます。

 

$P_{C1}$ $= 3 \cdot \left( \dfrac{V}{\sqrt{\left( r_1 + \dfrac{{r_2}^\prime}{s} \right)^2 + (x_1 + {x_2}^\prime )^2}} \right)^2$ $\cdot r_1$ $= \dfrac{3 V^2 \, r_1}{\left( r_1 + \dfrac{{r_2}^\prime}{s} \right)^2 + (x_1 + {x_2}^\prime )^2}$

 

 

 

三相分の二次入力P2の求め方

二次入力は等価回路の二次側の抵抗分で消費される電力になります。

 

等価回路より二次側の合成抵抗分を求めると、

 

${r_2}^\prime + \dfrac{1-s}{s} {r_2}^\prime = \left( 1 + \dfrac{1-s}{s} \right) {r_2}^\prime$ $= \left( \dfrac{s+1-s}{s} \right) {r_2}^\prime$ $= \dfrac{{r_2}^\prime}{s}$

 

$\therefore$ 二次側の合成抵抗分 $= \dfrac{{r_2}^\prime}{s}$

 

求めた二次側の合成抵抗分は一相分の抵抗分で、流れる電流は ${I_1}^\prime$ であるので、求める三相分の二次入力 $P_2$ は次のようになります。

 

$P_2 = 3 \times {{I_1}^\prime}^2 \, \dfrac{{r_2}^\prime}{s} = 3 \dfrac{{{I_1}^\prime}^2 \, {r_2}^\prime}{s}$

 

 

三相分の二次銅損PC2の求め方

二次銅損は二次抵抗 ${r_2}^\prime$ による損失であるので、一相分の二次銅損を ${P_{C2}}^\prime$ とすると ${P_{C2}}^\prime$ は次式となります。

 

${P_{C2}}^\prime = {{I_1}^\prime}^2 \, {r_2}^\prime$

 

したがって、三相分の二次銅損 $P_{C2}$ は一相分の二次銅損 ${P_{C2}}^\prime$ の3倍なので、

 

$P_{C2} = 3 \times {P_{C2}}^\prime = 3 {{I_1}^\prime}^2 \, {r_2}^\prime$

 

 

となります。

 

三相分の出力POの求め方

出力は等価回路の二次側の負荷抵抗 $\dfrac{1-s}{s} {r_2}^\prime$ で消費される電力になります。

 

 

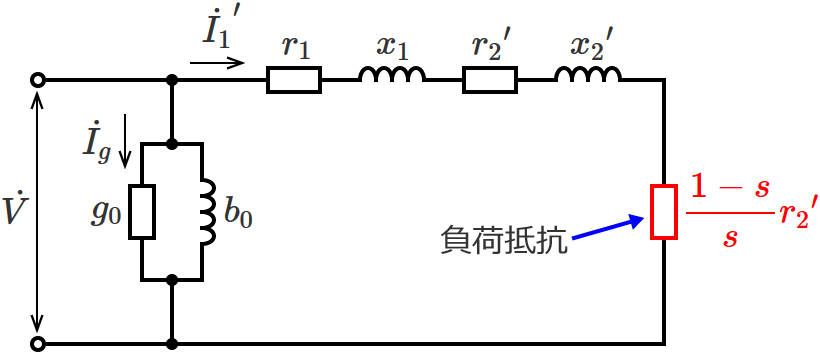
この負荷抵抗（等価回路）は一相分を表わしているので、求める三相分の出力 $P_o$ は次式となります。

 

$P_o = 3 \times {{I_1}^\prime}^2 \, \left( \dfrac{1-s}{s} {r_2}^\prime \right)$ $= 3 {{I_1}^\prime}^2 \, \left( \dfrac{1-s}{s} \right) {r_2}^\prime$

 

 

効率ηの求め方

効率は電動機の出力を電動機の入力で割ったもので表わされます。

 

ここで電動機の入力 $P_{in}$ は、電動機の出力＋電動機の損失分であるので、すなわち、

 

電動機の入力 $P_{in}$ ＝ 電動機の出力 $P_o$ ＋ 鉄損 $P_i$ ＋ 一次銅損 $P_{C1}$ ＋ 二次銅損 $P_{C2}$

 

となります。

 

したがって効率 $\eta$ は、

 

$\eta = \dfrac{P_o}{P_in} \times 100$ $= \dfrac{P_o}{P_o + P_i + P_{C1} + P_{C2}} \times 100$

 

 

となります。

 

等価回路のまとめ

等価回路の各抵抗とそれぞれの抵抗が表わす値

等価回路の各抵抗とそれぞれの抵抗が表わす値（意味）は、次の図のようになります。

 

 

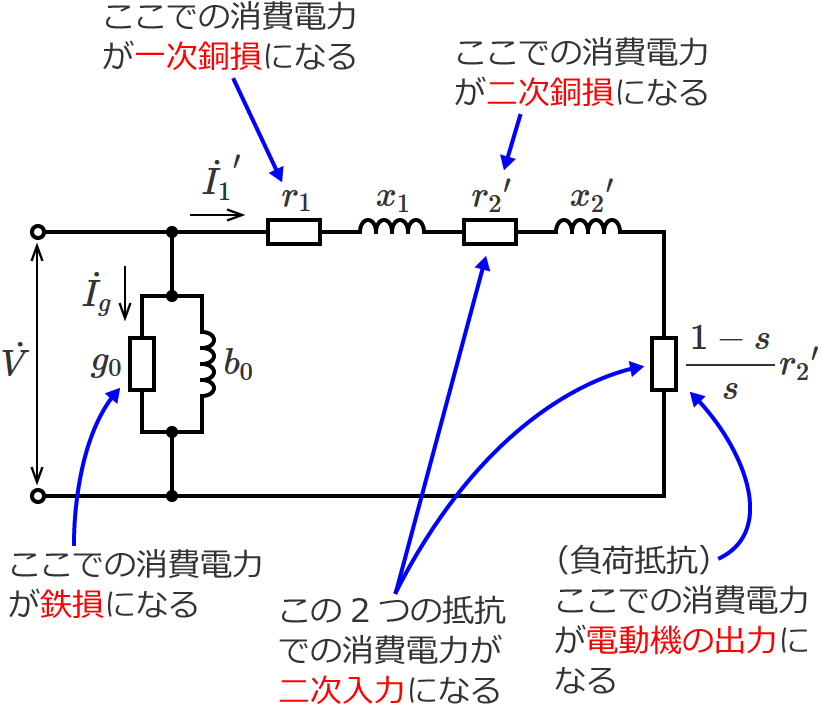
三相誘導電動機のL形等価回路の別表現

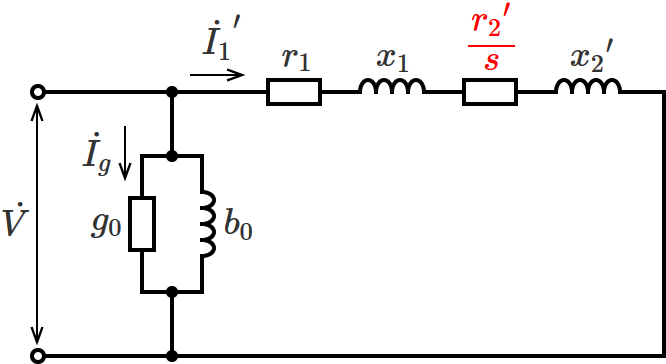
三相誘導電動機のL形等価回路は、${r_2}^\prime$ と $\dfrac{1-s}{s} {r_2}^\prime$ を合成した次のような等価回路で表わすこともあります。

 

 

 

誘導電動機の固定子巻線抵抗　←BACK

NEXT→　誘導電動機の無負荷試験

スポンサーリンク

誘導電動機のL形等価回路　関連ページ

直流発電機の誘導起電力

電気機器分野の「直流発電機の誘導起電力」についてまとめたページです。「直流発電機の誘導起電力」は第三種電気主任技術者試験（電験三種）でも出題される重要な項目です。誘導起電力の式の導出方法を理解して、公式をおぼえておきましょう。

直流分巻電動機の等価回路

電気機器分野の「直流分巻電動機の等価回路」についてまとめたページです。「直流分巻電動機」は第三種電気主任技術者試験（電験三種）でも出題される重要な項目です。等価回路の書き方、誘導起電力（逆起電力）、出力、トルクなどの求め方を理解しておきましょう。

直流他励電動機の等価回路

電気機器分野の「直流他励電動機の等価回路」についてまとめたページです。「直流他励電動機」は第三種電気主任技術者試験（電験三種）でも出題される重要な項目です。等価回路の書き方、誘導起電力（逆起電力）、回転速度、トルクなどの求め方を理解しておきましょう。

誘導電動機の同期速度

電気機器の「誘導電動機の同期速度」についてまとめたページです。「誘導電動機の同期速度」は第二種電気工事士試験、第三種電気主任技術者試験（電験三種）でも出題される重要な項目です。同期速度を与える式をおぼえておきましょう。

誘導電動機のすべり

電気機器の「誘導電動機のすべり」についてまとめたページです。「誘導電動機のすべり」は第三種電気主任技術者試験（電験三種）でも出題される重要な項目です。すべりを与える式をおぼえておきましょう。

誘導電動機のトルク

電気機器の「誘導電動機のトルク」についてまとめたページです。「誘導電動機のトルク」は第三種電気主任技術者試験（電験三種）でも出題される重要な項目です。トルクを与える式をおぼえておきましょう。

誘導電動機の固定子巻線抵抗

電気機器分野の「誘導電動機の固定子巻線抵抗」についてまとめたページです。「誘導電動機の固定子巻線抵抗」は第二種電気主任技術者試験（電験二種）でも出題される項目です。

誘導電動機の無負荷試験

電気機器の「誘導電動機の無負荷試験」についてまとめたページです。「誘導電動機の無負荷試験」は第三種電気主任技術者試験（電験三種）でも出題される重要な項目です。無負荷試験時の等価回路をおぼえておきましょう。

誘導電動機の拘束試験

電気機器の「誘導電動機の拘束試験」についてまとめたページです。「誘導電動機の拘束試験」は第三種電気主任技術者試験（電験三種）でも出題される重要な項目です。拘束試験時の等価回路をおぼえておきましょう。

誘導電動機のスターデルタ（Y-Δ）始動法

電気機器の「誘導電動機のスターデルタ始動法」についてまとめたページです。「誘導電動機のスターデルタ始動法」は第二種電気工事士や第三種電気主任技術者試験（電験三種）の機械科目でも出題される重要で基本的な項目です。

同期電動機の等価回路とベクトル図

電気機器分野の「同期電動機の等価回路」についてまとめたページです。「同期電動機の等価回路」は第三種電気主任技術者試験（電験三種）でも出題される重要な項目です。等価回路とベクトル図の書き方をおぼえておきましょう。

三相回路の基準インピーダンス・基準電流の式の導出

電気機器分野の「三相回路の基準インピーダンス・基準電流の式の導出」についてまとめたページです。「三相回路の基準インピーダンス・基準電流の式」は第三種電気主任技術者試験（電験三種）でも出題される重要な項目です。公式を暗記するだけではなく、式の導出方法をおぼえておきましょう。