スポンサーリンク
過渡現象とは
※ページ内にPR・広告が含まれる場合があります。
過渡現象とは、ある定常状態から別の定常状態に移るまでに起こる現象(電圧や電流などの時間的な変化)のことをいいます。
過渡現象は、スイッチを切り替えた場合や回路素子の値が変わった場合など、回路の状態が変化することによって起こり、過渡現象はコイルやコンデンサを含む回路で起こります。(コイルやコンデンサを含む回路であっても過渡現象が現われない特殊な場合もあるんですけどね。ここでは、それはおいといて…。)
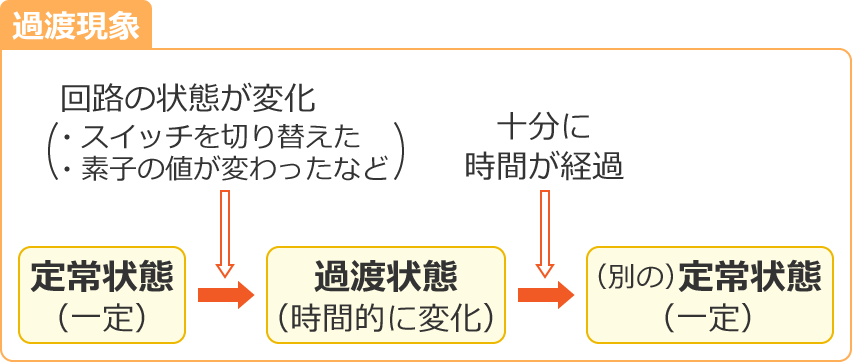
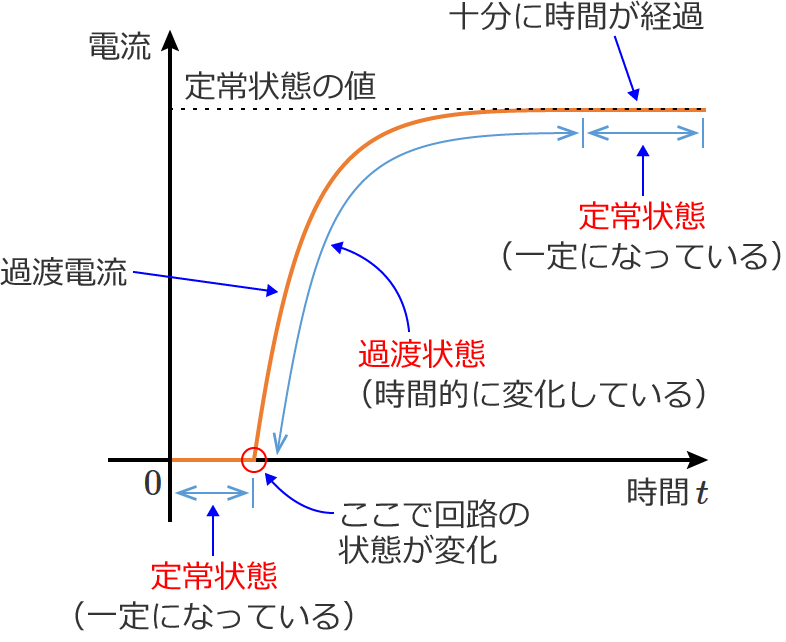
ちなみに、定常状態とは、時間が十分に経過し、電圧や電流などが一定の値になって変化していない状態、または、電圧や電流などが周期的に一定の繰り返しになっている状態のことをいいます。
また、過渡状態とは、ある定常状態から別の定常状態に移るまでの間の状態(時間的に変化している状態)のことをいいます。なお、このときに流れる電流を過渡電流といいます。
スポンサーリンク
過渡現象の例(RL直列回路)
次のように、$R$[$\Omega$]の抵抗、インダクタンス $L$[$\mathrm{H}$]のコイル、ⒶとⒷに接続を切り替えることができるスイッチ $\mathrm{S}$、$E$[$\mathrm{V}$]の直流電源からなるRL直列回路があるとします。
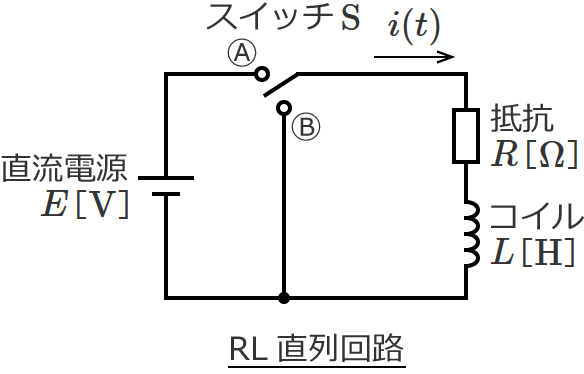
このRL直列回路のスイッチ $\mathrm{S}$ をⒷ側にして十分に時間がたった後、スイッチ $\mathrm{S}$ をⒶ側に切り替え、その後スイッチ $\mathrm{S}$ をまたⒷ側に切り替えると、この回路に流れる電流 $i(t)$ と回路の状態は以下のように変化し、過渡現象が現われます。
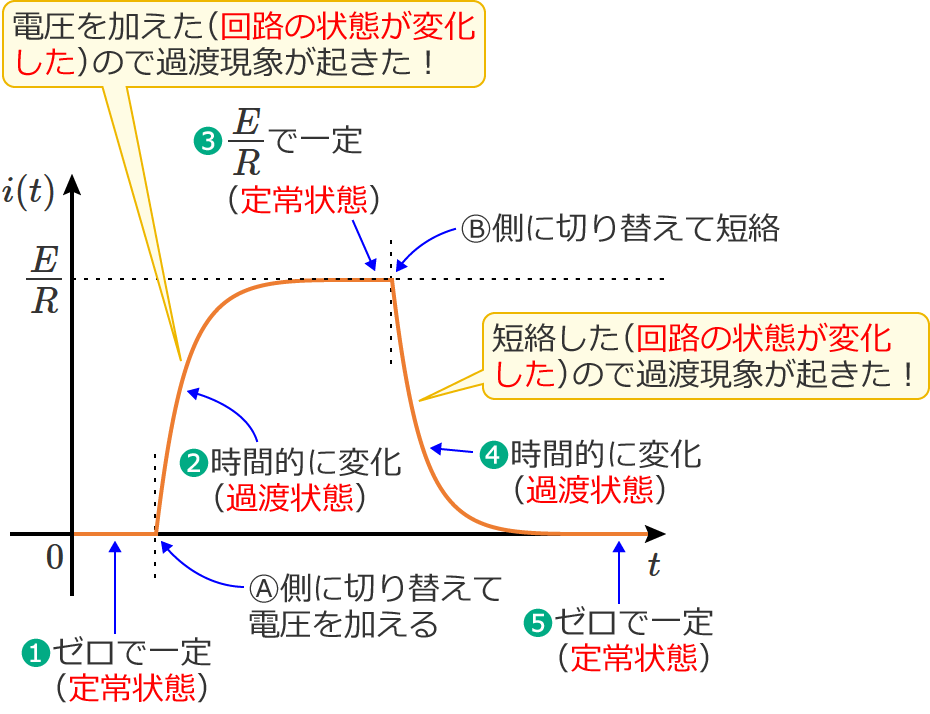
❶最初はスイッチ $\mathrm{S}$ がⒷ側になっているので、回路に流れる電流はゼロになります。(定常状態)
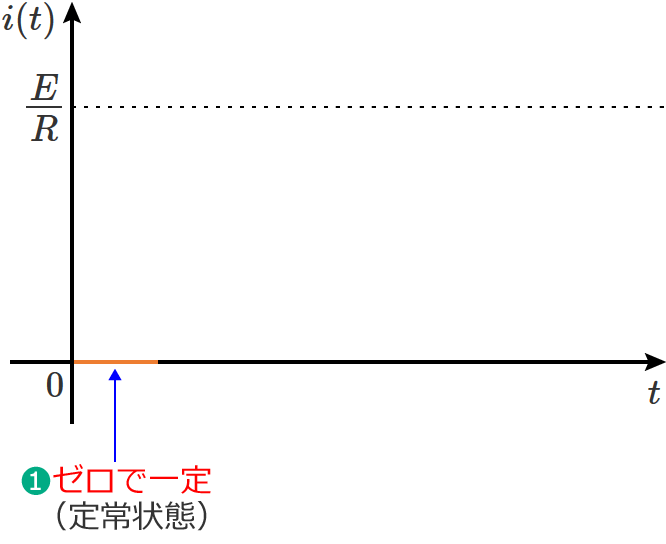
❷ここでスイッチ $\mathrm{S}$ をⒶ側に切り替えると、直流電源がつながって回路に電圧が加わるので電流が流れ、電流は次のように増加(時間的に変化)していきます。(過渡状態)
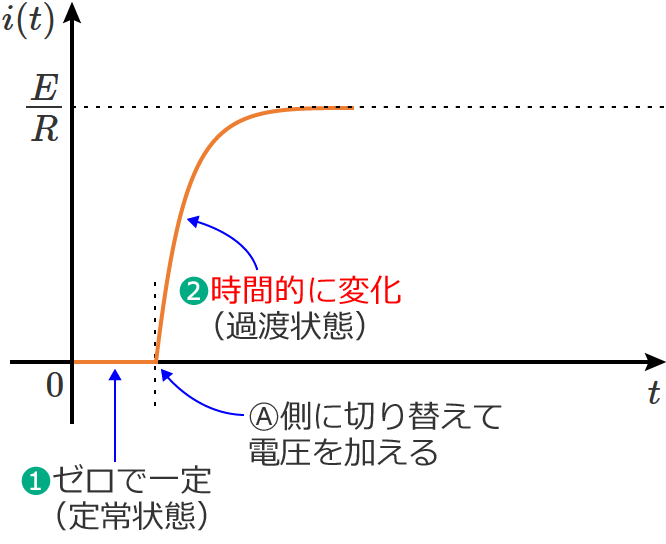
❸そして時間が十分に経過すると、回路には一定の電流( $E/R$ )が流れるようになります。(定常状態)
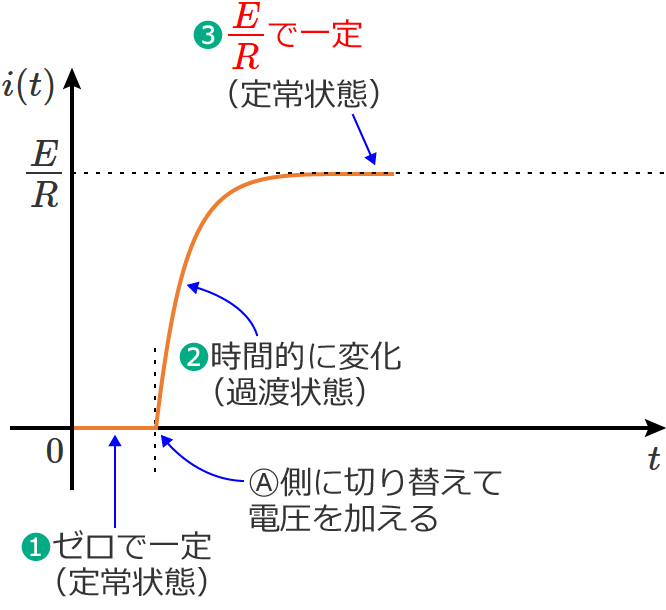
❹❸の定常状態においてスイッチ $\mathrm{S}$ をⒷ側に瞬時に切り替えると、回路に流れる電流は次のように減少(時間的に変化)していきます。(過渡状態)
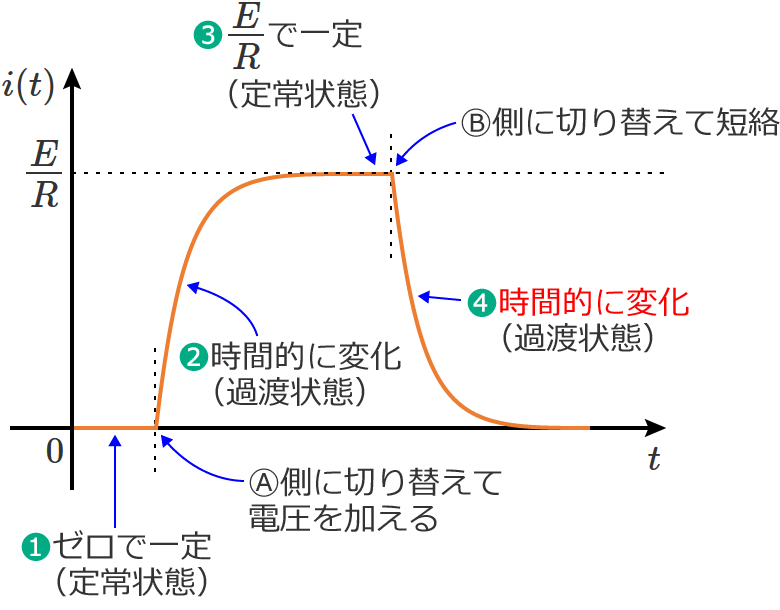
❺そして時間が十分に経過すると、回路に流れる電流はゼロになり、最初の状態❶に戻ります。(定常状態)
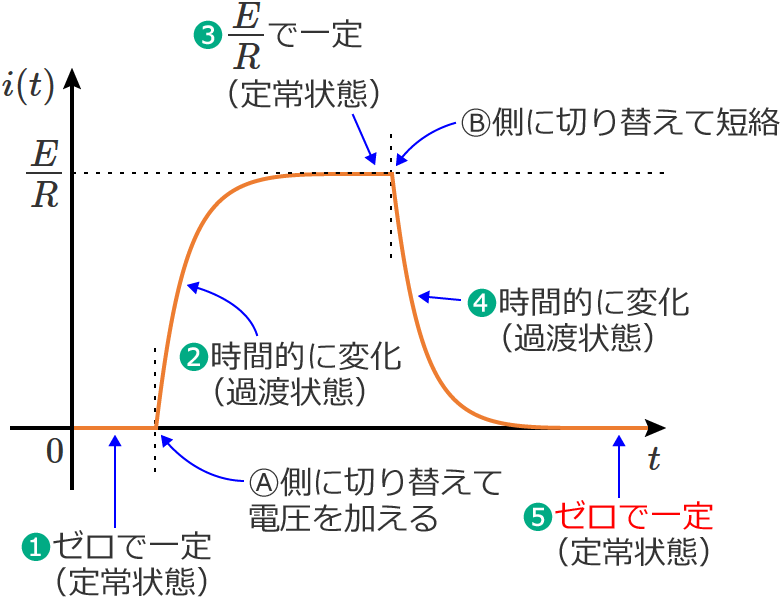
以上のように、スイッチ $\mathrm{S}$ をⒷ側からⒶ側に切り替えてRL直列回路に電圧を加え、その後スイッチ $\mathrm{S}$ をⒷ側に切り替えて短絡すると、回路は「定常状態 ⇨ 過渡状態 ⇨ 定常状態 ⇨ 過渡状態 ⇨ 定常状態」と変化し、「電圧を加えた場合」「その後、短絡した場合」それぞれで過渡現象が起こります。
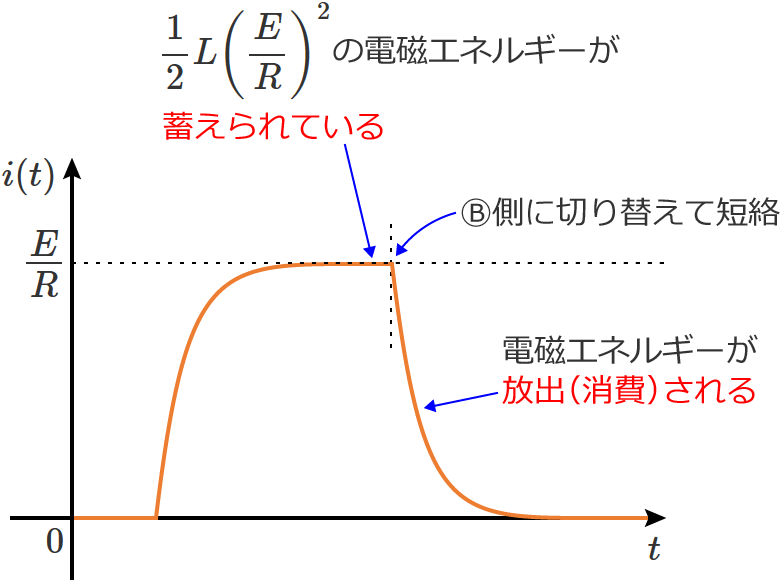
ちなみに、スイッチ $\mathrm{S}$ をⒷ側に切り替えて短絡する前まではコイルには $\dfrac{1}{2} L\left(\dfrac{E}{R}\right) ^2$ の電磁エネルギーが蓄えられていて、スイッチ $\mathrm{S}$ をⒷ側に切り替えるとこの電磁エネルギーは放出(抵抗 $R$ で消費)されます。この電磁エネルギーが消費されるまで回路には電流が流れ続けます。
スポンサーリンク
スポンサーリンク
過渡現象の例(RC直列回路)
もう一つだけ過渡現象の例を…。
次のように、$R$[$\Omega$]の抵抗、静電容量 $C$[$\mathrm{F}$]のコンデンサ、ⒶとⒷに接続を切り替えることができるスイッチ $\mathrm{S}$、$E$[$\mathrm{V}$]の直流電源からなるRC直列回路があるとします。
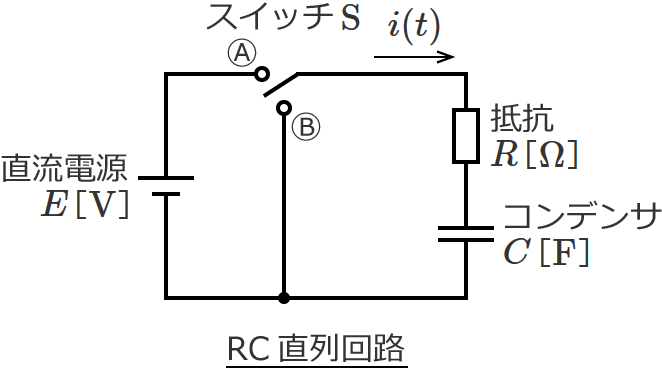
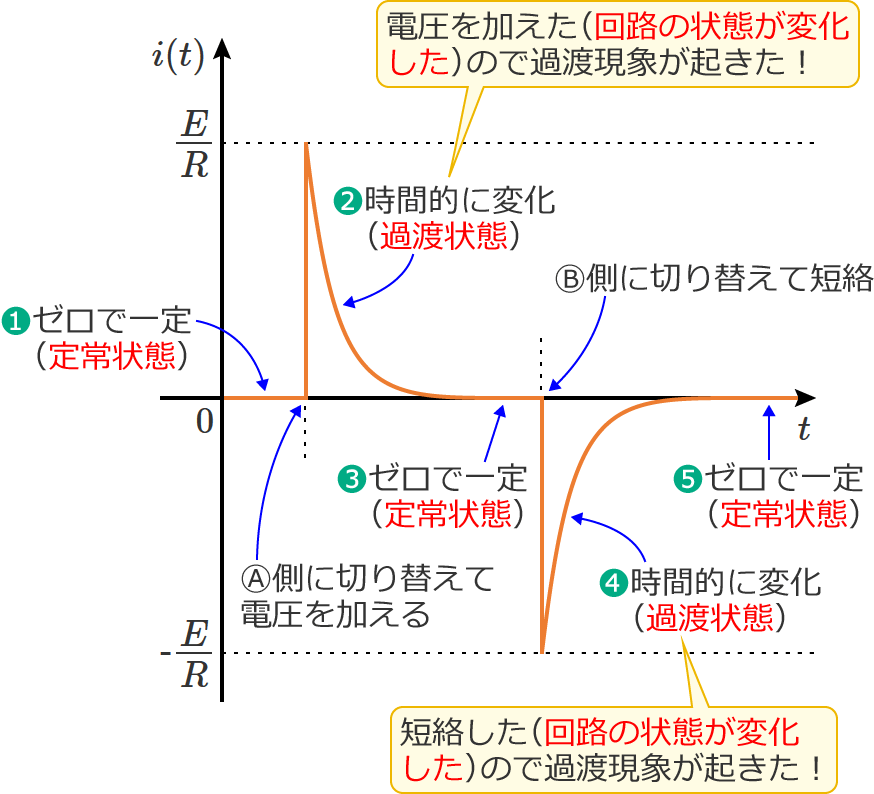
このRC直列回路のスイッチ $\mathrm{S}$ をⒷ側にして十分に時間がたった後、スイッチ $\mathrm{S}$ をⒶ側に切り替え、その後スイッチ $\mathrm{S}$ をまたⒷ側に切り替えると、この回路に流れる電流 $i(t)$ と回路の状態は以下のように変化し、過渡現象が現われます。
❶最初はスイッチ $\mathrm{S}$ がⒷ側になっているので、回路に流れる電流はゼロになります。(定常状態)
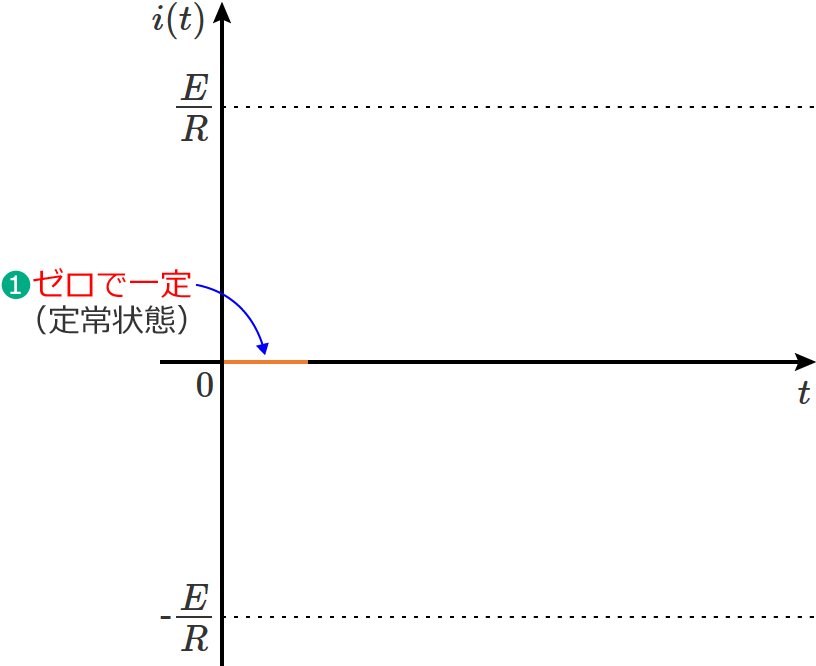
❷ここでスイッチ $\mathrm{S}$ をⒶ側に切り替えると、スイッチ $\mathrm{S}$ を切り替えた瞬間に電流は $E/R$ になり、その後電流は次のように減少(時間的に変化)していきます。(過渡状態)
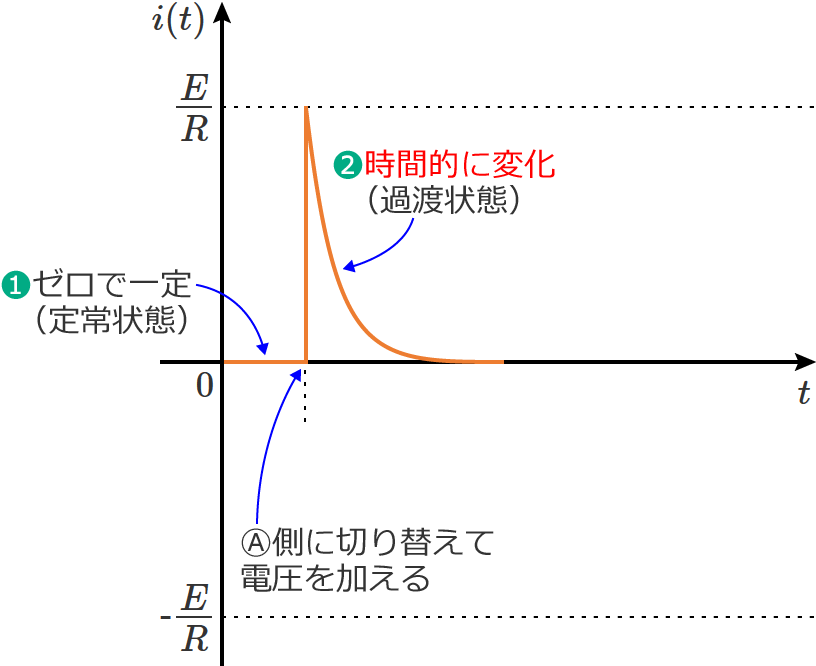
❸そして時間が十分に経過すると、回路の電流はゼロになります。(定常状態)
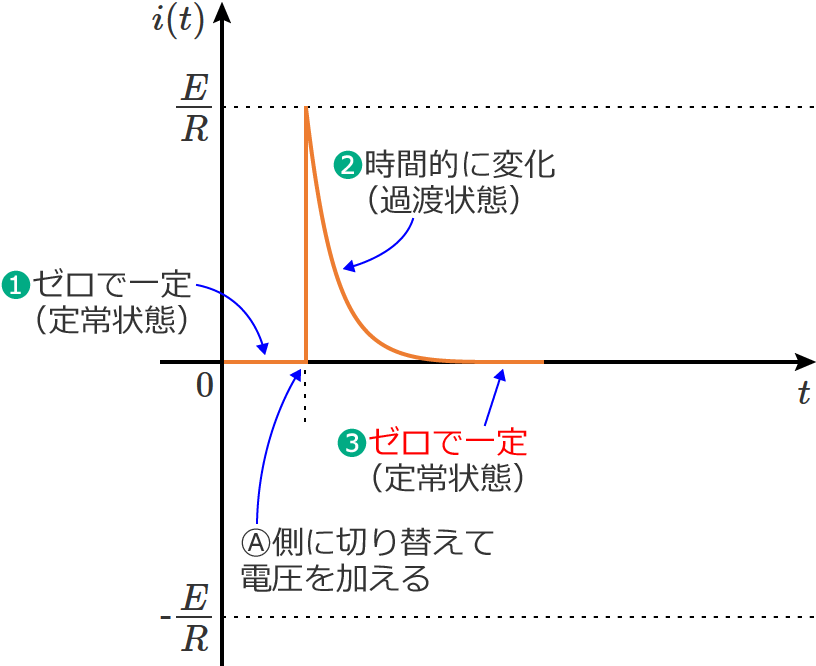
❹❸の定常状態においてスイッチ $\mathrm{S}$ をⒷ側に切り替えると、スイッチ $\mathrm{S}$ を切り替えた瞬間に電流は $-E/R$ になり、その後電流は次のように減少(時間的に変化)していきます。(過渡状態)
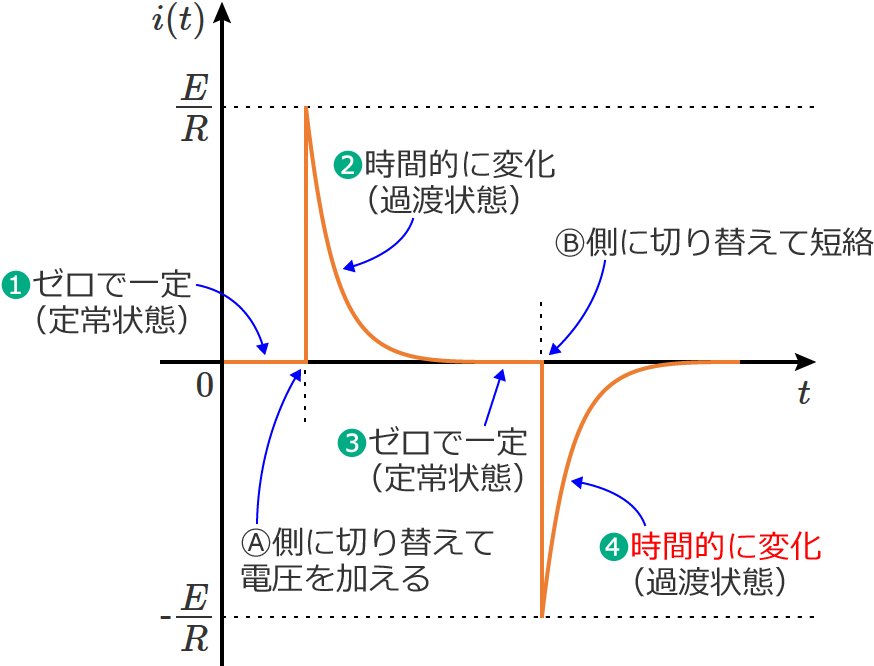
電流の向きが❷とは逆になるため、ここでの電流はマイナスになります。
❺そして時間が十分に経過すると、回路に流れる電流はゼロになり、最初の状態❶に戻ります。(定常状態)
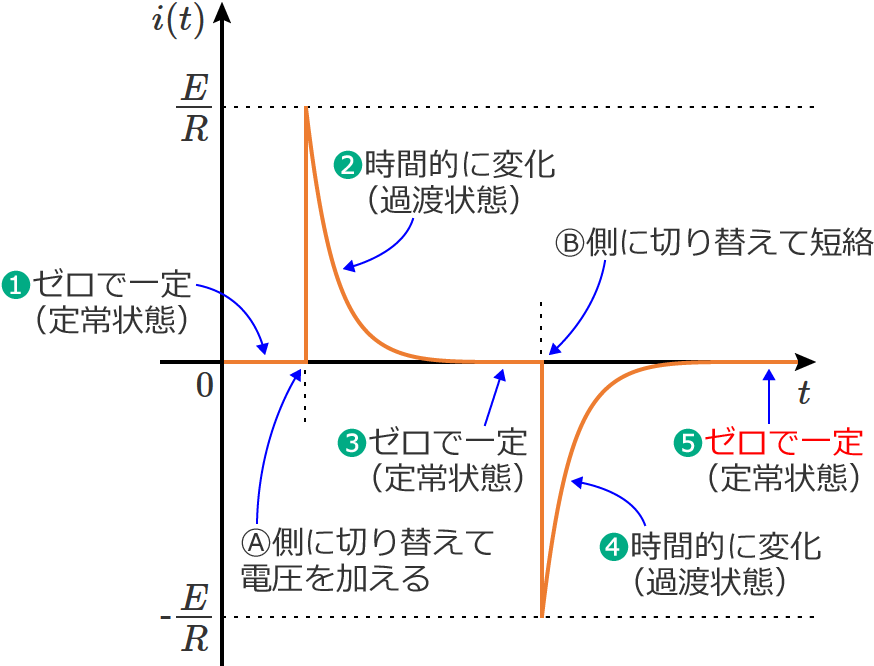
以上のように、スイッチ $\mathrm{S}$ をⒷ側からⒶ側に切り替えてRC直列回路に電圧を加え、その後スイッチ $\mathrm{S}$ をⒷ側に切り替えて短絡すると、回路は「定常状態 ⇨ 過渡状態 ⇨ 定常状態 ⇨ 過渡状態 ⇨ 定常状態」と変化し、「電圧を加えた場合」「その後、短絡した場合」それぞれで過渡現象が起こります。
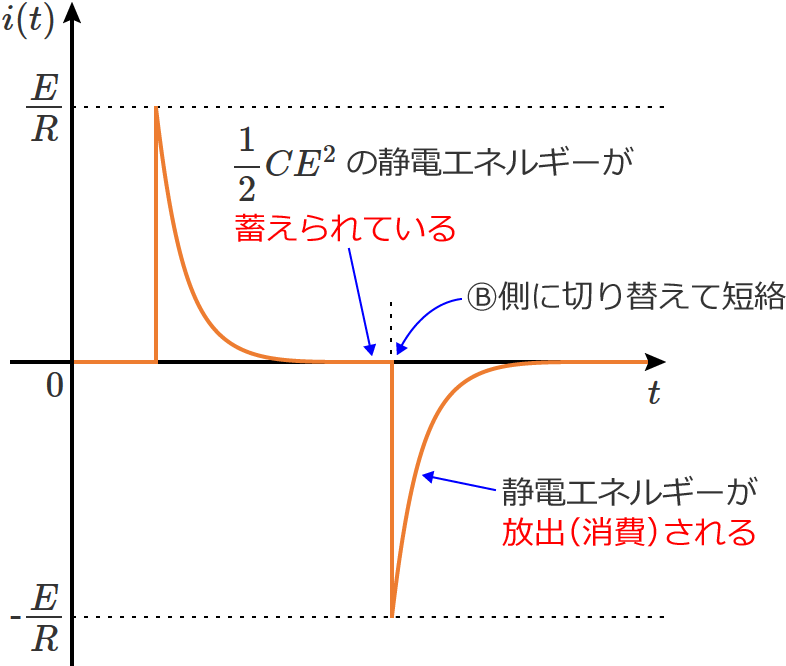
ちなみに、スイッチ $\mathrm{S}$ をⒷ側に切り替えて短絡する前まではコンデンサには $\dfrac{1}{2} CE^2$ の静電エネルギーが蓄えられていて、スイッチ $\mathrm{S}$ をⒷ側に切り替えると静電エネルギーは放出(抵抗 $R$ で消費)されます。この静電エネルギーが消費されるまで回路には電流が流れ続けます。
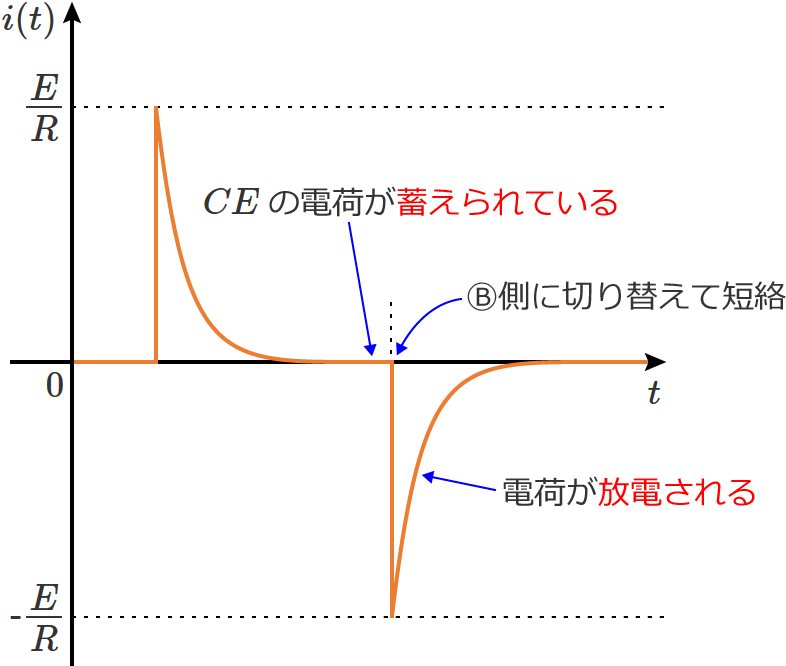
電荷でいえば…、
スイッチ $\mathrm{S}$ をⒷ側に切り替えて短絡する前まではコンデンサには $CE$ の電荷が蓄えられていて、スイッチ $\mathrm{S}$ をⒷ側に切り替えると電荷は放電されます。この放電が完了するまで回路には電流が流れ続けます。
となります。
- 過渡現象は、ある定常状態から別の定常状態に移るまでに起こる現象
- 過渡現象は、回路の状態が変化することによって起こる
- 過渡現象は、コイルやコンデンサを含む回路で起こる
スポンサーリンク
スポンサーリンク
電気のお勉強のTOP ←BACK
NEXT→ 時定数
スポンサーリンク
過渡現象とは 関連ページ
- 時定数
- 過渡現象の時定数について解説しています。時定数は、過渡状態での変化の速さを表わす量で、時定数が小さければ変化する速さは速くなり、時定数が大きければ変化する速さは遅くなります。
- 時定数の単位はなぜ時間s(秒)になるのか?
- 過渡現象の時定数の単位はなぜ時間s(秒)になるのか?について解説しています。時定数の単位が時間(s)になる過程も詳しく書いていますので、参考にしてみてください。
- RL直列回路の時定数(τ=L/R)の導出
- RL直列回路の時定数(τ=L/R)の導出方法について解説しています。RL直列回路の時定数は、電流のt=0における接線と定常状態の電流を表わす直線との交点の時間を算出すると求められます。
- RC直列回路の時定数(τ=CR)の導出
- RC直列回路の時定数(τ=CR)の導出方法について解説しています。RC直列回路の時定数は、電流のt=0における接線と定常状態の電流を表わす直線との交点の時間を算出すると求められます。
- RL直列回路の過渡現象の解き方
- RL直列回路の過渡現象の解き方について解説しています。過渡現象を解くためには微分方程式を解く必要があるため計算がちょっと大変ですが、解き方のパターンをおぼえてしまうとそれほど難しくはありませんよ。
- RC直列回路の過渡現象の解き方
- RC直列回路の過渡現象の解き方について解説しています。RC直列回路の過渡現象はRL直列回路よりもちょっとだけ計算が大変ですが、解き方のパターンは同じなので、おぼえてしまうとそれほど難しくはありませんよ。
- ラプラス変換によるRL直列回路の過渡現象の解き方
- ラプラス変換によるRL直列回路の過渡現象の解き方について解説しています。ラプラス変換を使ってRL直列回路の過渡現象を解いていますので、ラプラス変換を使った過渡現象の解き方の参考にしてみてください。
- ラプラス変換によるRC直列回路の過渡現象の解き方
- ラプラス変換によるRC直列回路の過渡現象の解き方について解説しています。ラプラス変換を使ってRC直列回路の過渡現象を解いていますので、ラプラス変換を使った過渡現象の解き方の参考にしてみてください。


