RC直列回路の時定数（τ＝CR）の導出

※ページ内にPR･広告が含まれる場合があります。

次のように、抵抗 $R$、コンデンサ $C$、直流電源、スイッチからなるRC直列回路があるとします。

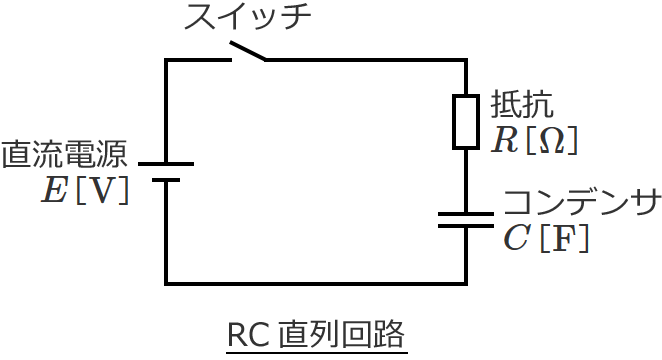
RC直列回路

このRC直列回路の時定数 $\tau$ は、よく知られているように $\tau =CR$ です。

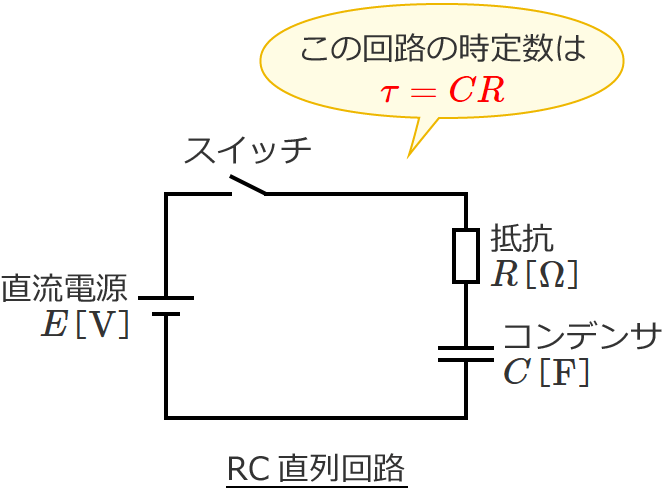
RC直列回路の時定数はτ＝CR

この $\tau =CR$ は、参考書などにも公式としてよく書かれているので、RC直列回路の時定数を求めるときは、

$\tau =CR$ にコンデンサの静電容量の値 $C$ と抵抗 $R$ の値を代入して…、時定数でた！

みたいな感じで使っていると思います。（たぶん）

このようによく使う $\tau =CR$ ですが、RC直列回路の時定数は、なぜ $CR$ になるのでしょうか？

RC直列回路の電流の過渡現象を表わす式を使って、RC直列回路の時定数 $\tau =CR$ を導いてみました。

RC直列回路の時定数の導出

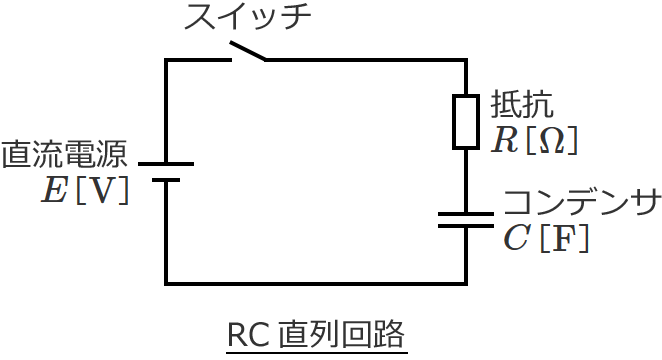
RC直列回路

上の図のようなRC直列回路において、$t=0$ でスイッチをONすると次のように電流が流れます。（コンデンサ $C$ に蓄えられている初期電荷はないもの（ゼロ）とします。）

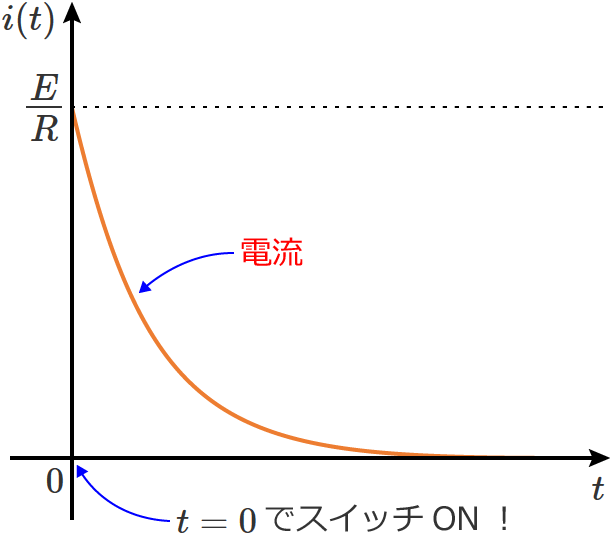
RC直列回路に流れる電流

このとき、この曲線の $t=0$ における接線を引くと、接線は、$t=0$ から「ある時間」のところで定常状態の電流値（ $i(t)=0$ の直線）と交わります。

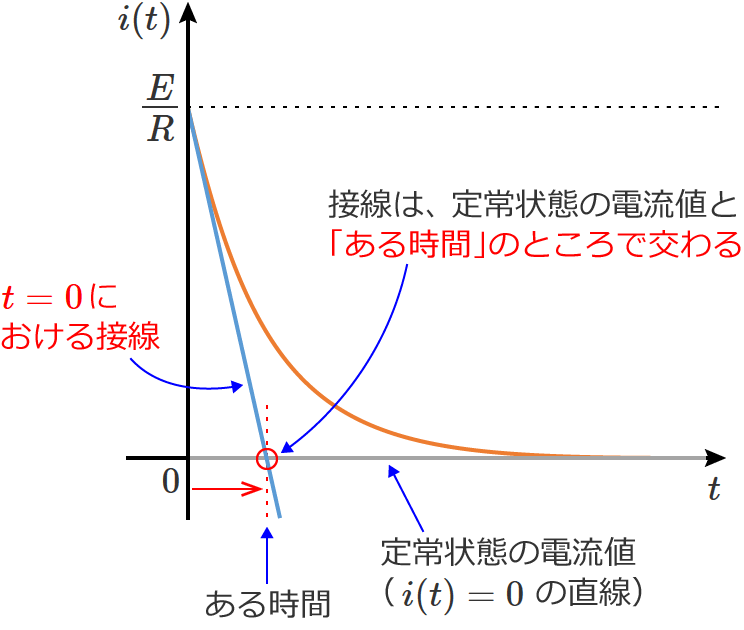
接線はある時間のところで定常状態の電流値（ゼロ）と交わる

この「ある時間」が時定数になるので、$t=0$ から2つの直線の交点までの時間を求めれば、それが時定数になります。

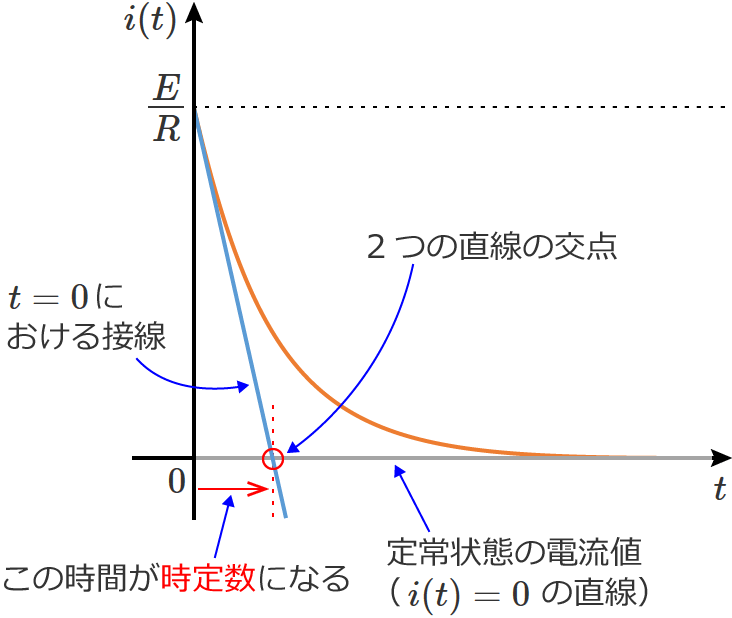
2つの直線の交点までの時間が時定数

では、$t=0$ から2つの直線の交点までの時間を求めてみます。

初めに、$t=0$ における接線の式を求めます。

RC直列回路において、$t=0$ でスイッチをONしてから電流が定常状態になるまでの式（RC直列回路の電流の過渡現象を表わす式）は、次の図中の①式で表わされます。

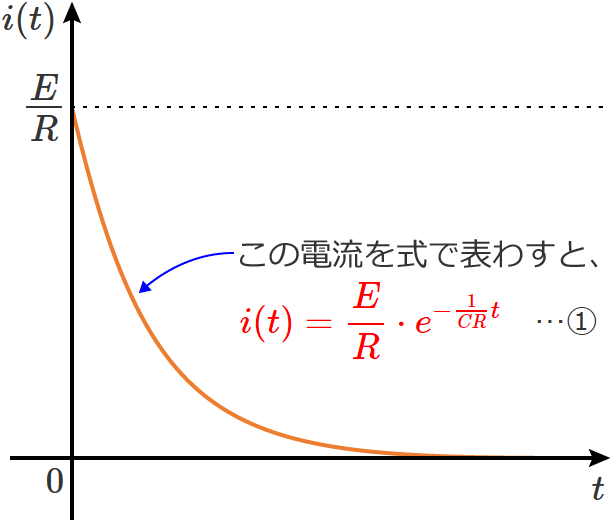
RC直列回路の電流の過渡現象を表わす式

この①式を $t$ で微分して $t=0$ を代入すると、$t=0$ における接線の傾きが求められます。①式を $t$ で微分すると、

$\dfrac{d\, i(t)}{dt} =\dfrac{E}{R}\cdot\left( -\dfrac{1}{CR}\right)\cdot e^{-\frac{1}{CR} t}$

$\therefore\dfrac{d\, i(t)}{dt} =-\dfrac{E}{CR^2}\cdot e^{-\frac{1}{CR} t}$

となり、これに $t=0$ を代入すると、

$\dfrac{d\, i(0)}{dt} =-\dfrac{E}{CR^2}\cdot e^{-\frac{1}{CR}\times 0}$

$\therefore\dfrac{d\, i(0)}{dt} =-\dfrac{E}{CR^2}$　…②　（$t=0$ における接線の傾き）

となります。この②が $t=0$ における接線の傾きになり、接線は点 $\left( 0\, ,\, \dfrac{E}{R}\right)$ を通るので、$t=0$ における接線の式は次のようになります。

$\therefore i(t)=-\dfrac{E}{CR^2} t+\dfrac{E}{R}$　…③　（$t=0$ における接線の式）

$t=0$ のときの電流値は $\dfrac{E}{R}$ なので、$t=0$ における接線は点 $\left( 0\, ,\, \dfrac{E}{R}\right)$ を通ります。

$t=0$ における接線の式が求められたので、次は、③式の直線と $i(t)=0$ の直線（定常状態の電流値を表わす直線）が交わる時間を求めます。

$-\dfrac{E}{CR^2} t+\dfrac{E}{R} =0$

として、これを $t$ について解きます。すると、

$\dfrac{E}{CR^2} t=\dfrac{E}{R}$

$\dfrac{1}{CR} t=1$

$\therefore t=CR$

となり、2つの直線が交わる時間（ $t=0$ から2つの直線の交点までの時間）は $t=CR$ と求められました。

この時間が時定数になるので、RC直列回路の時定数 $\tau$ は、

$\tau =CR$　（RC直列回路の時定数）

になります。

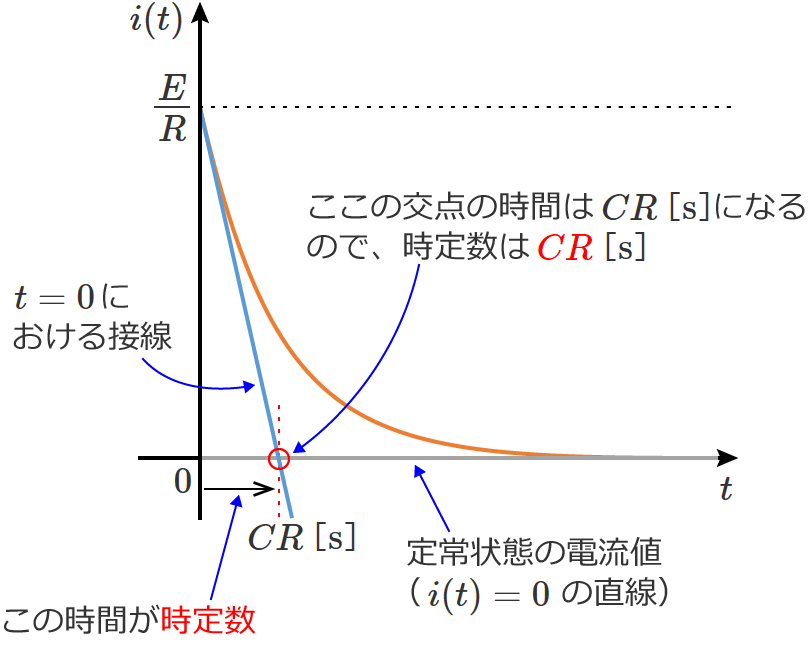
2直線の交点の時間がCR（時定数）になる

RC直列回路の時定数の導出のまとめ

「電流の過渡現象を表わす式の $t=0$ における接線」と「 $i(t)=0$ の直線」が交わる時間を求めると、RC直列回路の時定数（ $\tau =CR$ ）が求められる

時定数については、こちらの時定数のページを参考にしてみてください。
RL直列回路の時定数（ $\tau =L/R$ ）の導出については、こちらのRL直列回路の時定数の導出のページを参考にしてみてください。

RL直列回路の時定数（τ＝L/R）の導出　←BACK

NEXT→　RL直列回路の過渡現象の解き方

RC直列回路の時定数（τ＝CR）の導出　関連ページ

過渡現象とは: 過渡現象について解説しています。過渡現象とは、ある定常状態から別の定常状態に移るまでに起こる現象（電圧や電流などの時間的な変化）のことをいい、過渡現象は回路の状態が変化することによって起こります。
時定数: 過渡現象の時定数について解説しています。時定数は、過渡状態での変化の速さを表わす量で、時定数が小さければ変化する速さは速くなり、時定数が大きければ変化する速さは遅くなります。
時定数の単位はなぜ時間s（秒）になるのか？: 過渡現象の時定数の単位はなぜ時間s（秒）になるのか？について解説しています。時定数の単位が時間（s）になる過程も詳しく書いていますので、参考にしてみてください。
RL直列回路の時定数（τ＝L/R）の導出: RL直列回路の時定数（τ＝L/R）の導出方法について解説しています。RL直列回路の時定数は、電流のt=0における接線と定常状態の電流を表わす直線との交点の時間を算出すると求められます。
RL直列回路の過渡現象の解き方: RL直列回路の過渡現象の解き方について解説しています。過渡現象を解くためには微分方程式を解く必要があるため計算がちょっと大変ですが、解き方のパターンをおぼえてしまうとそれほど難しくはありませんよ。
RC直列回路の過渡現象の解き方: RC直列回路の過渡現象の解き方について解説しています。RC直列回路の過渡現象はRL直列回路よりもちょっとだけ計算が大変ですが、解き方のパターンは同じなので、おぼえてしまうとそれほど難しくはありませんよ。
ラプラス変換によるRL直列回路の過渡現象の解き方: ラプラス変換によるRL直列回路の過渡現象の解き方について解説しています。ラプラス変換を使ってRL直列回路の過渡現象を解いていますので、ラプラス変換を使った過渡現象の解き方の参考にしてみてください。
ラプラス変換によるRC直列回路の過渡現象の解き方: ラプラス変換によるRC直列回路の過渡現象の解き方について解説しています。ラプラス変換を使ってRC直列回路の過渡現象を解いていますので、ラプラス変換を使った過渡現象の解き方の参考にしてみてください。

過渡現象｜RC直列回路の時定数（τ＝CR）の導出