時定数の単位はなぜ時間s（秒）になるのか？

※ページ内にPR･広告が含まれる場合があります。

時定数の単位はよく知られているように、時間 ${\mathbf{s}}$（秒）になります。

例えば、RL直列回路の過渡現象の時定数は $\tau =\dfrac{L}{R}$ $\left[\,\mathrm{s}\,\right]$ になり、

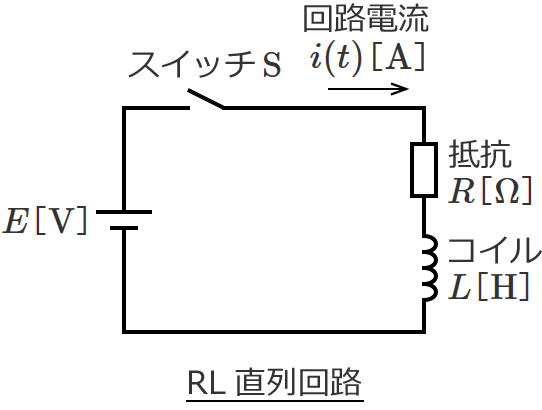
RL直列回路

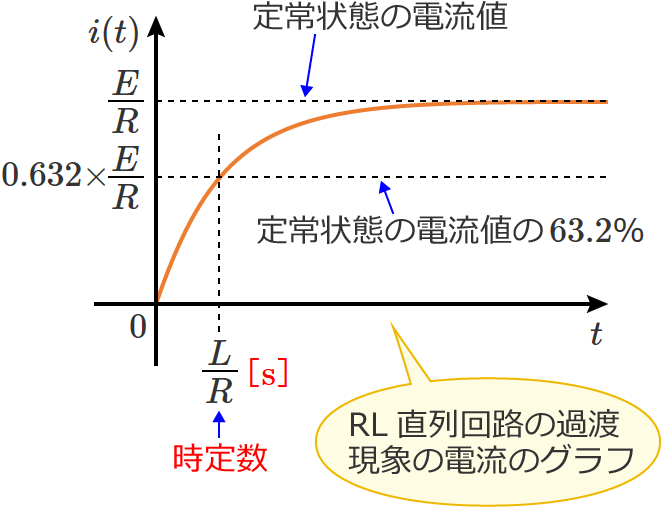
RL直列回路の時定数

RC直列回路の過渡現象の時定数は $\tau =CR$ $\left[\,\mathrm{s}\,\right]$ になります。

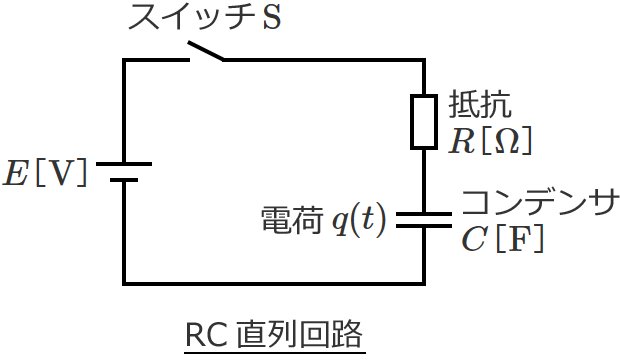
RC直列回路

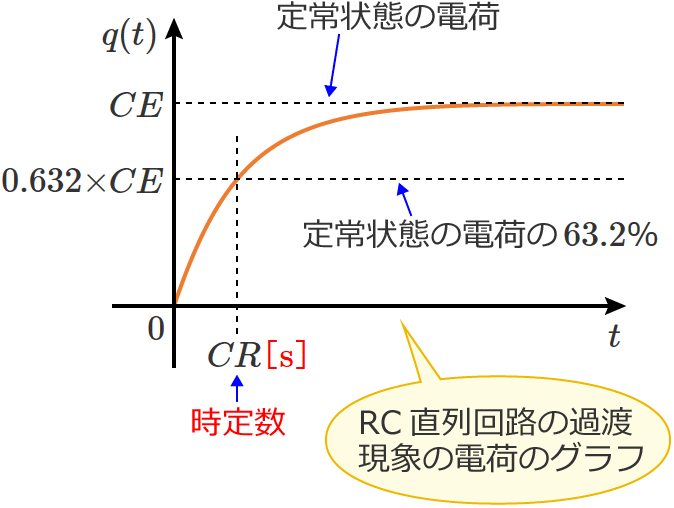
RC直列回路の時定数

でも、この時定数の単位ってなんか変な感じがしますよね。

コイルのインダクタンス $L$ の単位は $\left[\,\mathrm{H}\,\right]$（ヘンリー）で、抵抗 $R$ の単位は $\left[\,\Omega\,\right]$（オーム）で、コンデンサの静電容量 $C$ の単位は $\left[\,\mathrm{F}\,\right]$（ファラド）ですよね。

なので、RL直列回路の時定数は $L$ を $R$ で割っているので $\dfrac{\left[\,\mathrm{H}\,\right]}{\left[\,\Omega\,\right]}$ なんですが、なんでこれが時間の単位 $\left[\,\mathrm{s}\,\right]$ になるの？？

RC直列回路の時定数は $C$ に $R$ をかけるので $\left[\,\mathrm{F}\,\right]\times\left[\,\Omega\,\right]$ なんですが、なんでこれが時間の単位 $\left[\,\mathrm{s}\,\right]$ になるの？？

このページでは、時定数の単位がなぜ時間 $\mathrm{s}$（秒）になるのかについて解説しますので、

なんで、時定数の単位は時間 $\mathrm{s}$（秒）なの？

なんて方は、続きを読んでみてください。

時定数の単位が時間s（秒）になる理由

RL直列回路の時定数の単位

まず初めに、RL直列回路の過渡現象の時定数 $\tau =\dfrac{L}{R}$ について考えてみます。

コイルにかかる電圧とコイルに流れる電流の関係は、電圧を $v \ \left[\,\mathrm{V}\,\right]\,$、電流を $i \ \left[\,\mathrm{A}\,\right]\,$、コイルのインダクタンスを $L \ \left[\,\mathrm{H}\,\right]$ とすると、

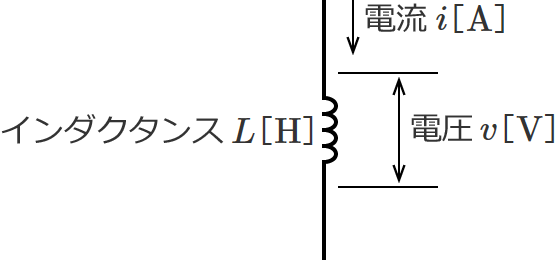
コイルの電圧、電流、インダクタンス

$v=L\dfrac{di}{dt}$　（コイルにかかる電圧と電流の関係）

で表わされます。これを次元で表わすと、

$\left[\,\mathrm{V}\,\right] =\left[\,\mathrm{H}\,\right]\dfrac{\left[\,\mathrm{A}\,\right]}{\left[\,\mathrm{s}\,\right]}$　…①

となります。なので、①を $\left[\,\mathrm{H}\,\right] =$ … に変形すると、

$\left[\,\mathrm{H}\,\right] =\dfrac{\left[\,\mathrm{V}\,\right]}{\left[\,\mathrm{A}\,\right]}\left[\,\mathrm{s}\,\right]$　…②

となり、$\left[\,\mathrm{H}\,\right]$ は $\dfrac{\left[\,\mathrm{V}\,\right]}{\left[\,\mathrm{A}\,\right]}\left[\,\mathrm{s}\,\right]$ と表わせます。

また、オームの法則より抵抗 $R \ \left[\,\Omega\,\right]$ は、電圧を $v \ \left[\,\mathrm{V}\,\right]\,$、電流を $i \ \left[\,\mathrm{A}\,\right]$ とすると、

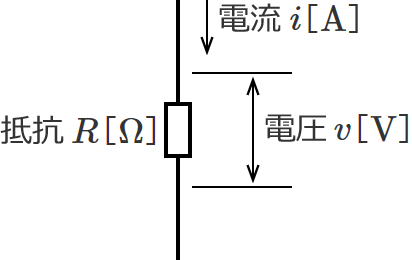
抵抗の電圧、電流、抵抗

$R=\dfrac{v}{i}$　（オームの法則）

で表わされます。これも次元で表わすと、

$\left[\,\Omega\,\right] =\dfrac{\left[\,\mathrm{V}\,\right]}{\left[\,\mathrm{A}\,\right]}$　…③

となります。③より $\dfrac{\left[\,\mathrm{V}\,\right]}{\left[\,\mathrm{A}\,\right]}$ は $\left[\,\Omega\,\right]$ なので、これを②に代入すると、

$\left[\,\mathrm{H}\,\right] =\left[\,\Omega\,\right]\left[\,\mathrm{s}\,\right]$　となるので、

$\therefore\dfrac{\left[\,\mathrm{H}\,\right]}{\left[\,\Omega\,\right]} =\left[\,\mathrm{s}\,\right]$　（RL直列回路の時定数の単位）

となります。したがって、時定数 $\tau =\dfrac{L\left[\,\mathrm{H}\,\right]}{R\left[\,\Omega\,\right]}$ は時間 $\left[\,\mathrm{s}\,\right]$ の次元になるので、時定数の単位は時間 $\mathrm{s}$（秒）になります。

以上のように、「コイルにかかる電圧と電流の関係」と「オームの法則」を使うと、RL直列回路の時定数の単位が時間 $\mathrm{s}$（秒）になることが分かります。

RC直列回路の時定数の単位

次は、RC直列回路の過渡現象の時定数 $\tau =CR$ について考えてみます。単位の導き方は、RL直列回路の場合と同じようなやり方です。

コンデンサに蓄えられる電荷とコンデンサにかかる電圧の関係は、電荷を $q \ \left[\,\mathrm{C}\,\right]\,$、電圧を $v \ \left[\,\mathrm{V}\,\right]\,$、コンデンサの静電容量を $C \ \left[\,\mathrm{F}\,\right]$ とすると、

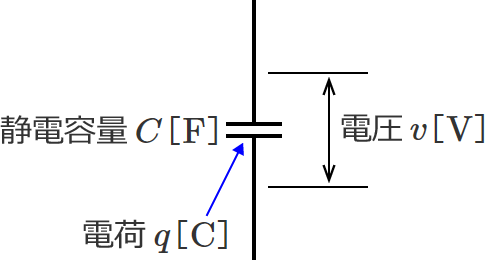
コンデンサの電圧、電荷、静電容量

$q=C\,v$　（コンデンサに蓄えられる電荷と電圧の関係）

で表わされます。これを次元で表わすと、

$\left[\,\mathrm{C}\,\right] =\left[\,\mathrm{F}\,\right]\left[\,\mathrm{V}\,\right]$　…④

となります。なので、④を $\left[\,\mathrm{F}\,\right] =$ … に変形すると、

$\left[\,\mathrm{F}\,\right] =\dfrac{\left[\,\mathrm{C}\,\right]}{\left[\,\mathrm{V}\,\right]}$　…⑤

となり、$\left[\,\mathrm{F}\,\right]$ は $\dfrac{\left[\,\mathrm{C}\,\right]}{\left[\,\mathrm{V}\,\right]}$ と表わせます。

また、電流と電荷の関係は、電荷を $q \ \left[\,\mathrm{C}\,\right]\,$、電流を $i \ \left[\,\mathrm{A}\,\right]$ とすると、

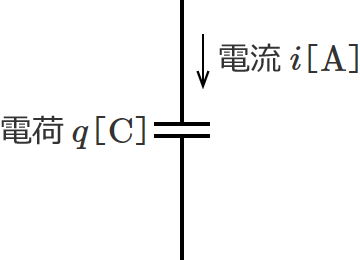
コンデンサの電流、電荷

$i=\dfrac{dq}{dt}$　（電流と電荷の関係）

で表わされます。これも次元で表わすと、

$\left[\,\mathrm{A}\,\right] =\dfrac{\left[\,\mathrm{C}\,\right]}{\left[\,\mathrm{s}\,\right]}$

$\therefore\left[\,\mathrm{C}\,\right] =\left[\,\mathrm{A}\,\right]\left[\,\mathrm{s}\,\right]$　…⑥

となります。⑥より $\left[\,\mathrm{C}\,\right]$ は $\left[\,\mathrm{A}\,\right]\left[\,\mathrm{s}\,\right]$ なので、これを⑤に代入すると、

$\left[\,\mathrm{F}\,\right] =\dfrac{\left[\,\mathrm{C}\,\right]}{\left[\,\mathrm{V}\,\right]} =\dfrac{\left[\,\mathrm{A}\,\right]\left[\,\mathrm{s}\,\right]}{\left[\,\mathrm{V}\,\right]}$

$\therefore\left[\,\mathrm{F}\,\right] =\dfrac{\left[\,\mathrm{A}\,\right]}{\left[\,\mathrm{V}\,\right]}\left[\,\mathrm{s}\,\right]$　…⑦

となります。ここで、$\dfrac{\left[\,\mathrm{A}\,\right]}{\left[\,\mathrm{V}\,\right]}$ は $\dfrac{1}{\left[\,\Omega\,\right]}$ なので、これを⑦に代入すると、

$\left[\,\mathrm{F}\,\right] =\dfrac{\left[\,\mathrm{A}\,\right]}{\left[\,\mathrm{V}\,\right]}\left[\,\mathrm{s}\,\right] =\dfrac{\left[\,\mathrm{s}\,\right]}{\left[\,\Omega\,\right]}$　となるので、

$\therefore\left[\,\mathrm{F}\,\right]\left[\,\Omega\,\right] =\left[\,\mathrm{s}\,\right]$　（RC直列回路の時定数の単位）

となります。したがって、時定数 $\tau =C\left[\,\mathrm{F}\,\right]\times R\left[\,\Omega\,\right]$ は時間 $\left[\,\mathrm{s}\,\right]$ の次元になるので、時定数の単位は時間 $\mathrm{s}$（秒）になります。

以上のように、「コンデンサに蓄えられる電荷と電圧の関係」と「電流と電荷の関係」を使うと、RC直列回路の時定数の単位が時間 $\mathrm{s}$（秒）になることが分かります。

時定数については、こちらの時定数のページも参考にしてみてください。こちらのページでは、時定数と回路素子の値の関係や時定数と電流値の関係などについても解説しています。

時定数　←BACK

NEXT→　RL直列回路の時定数（τ＝L/R）の導出

時定数の単位はなぜ時間s（秒）になるのか？　関連ページ

過渡現象とは: 過渡現象について解説しています。過渡現象とは、ある定常状態から別の定常状態に移るまでに起こる現象（電圧や電流などの時間的な変化）のことをいい、過渡現象は回路の状態が変化することによって起こります。
時定数: 過渡現象の時定数について解説しています。時定数は、過渡状態での変化の速さを表わす量で、時定数が小さければ変化する速さは速くなり、時定数が大きければ変化する速さは遅くなります。
RL直列回路の時定数（τ＝L/R）の導出: RL直列回路の時定数（τ＝L/R）の導出方法について解説しています。RL直列回路の時定数は、電流のt=0における接線と定常状態の電流を表わす直線との交点の時間を算出すると求められます。
RC直列回路の時定数（τ＝CR）の導出: RC直列回路の時定数（τ＝CR）の導出方法について解説しています。RC直列回路の時定数は、電流のt=0における接線と定常状態の電流を表わす直線との交点の時間を算出すると求められます。
RL直列回路の過渡現象の解き方: RL直列回路の過渡現象の解き方について解説しています。過渡現象を解くためには微分方程式を解く必要があるため計算がちょっと大変ですが、解き方のパターンをおぼえてしまうとそれほど難しくはありませんよ。
RC直列回路の過渡現象の解き方: RC直列回路の過渡現象の解き方について解説しています。RC直列回路の過渡現象はRL直列回路よりもちょっとだけ計算が大変ですが、解き方のパターンは同じなので、おぼえてしまうとそれほど難しくはありませんよ。
ラプラス変換によるRL直列回路の過渡現象の解き方: ラプラス変換によるRL直列回路の過渡現象の解き方について解説しています。ラプラス変換を使ってRL直列回路の過渡現象を解いていますので、ラプラス変換を使った過渡現象の解き方の参考にしてみてください。
ラプラス変換によるRC直列回路の過渡現象の解き方: ラプラス変換によるRC直列回路の過渡現象の解き方について解説しています。ラプラス変換を使ってRC直列回路の過渡現象を解いていますので、ラプラス変換を使った過渡現象の解き方の参考にしてみてください。

電気のお勉強｜過渡現象｜時定数の単位はなぜ時間s（秒）になるのか？