スポンサーリンク
時定数
※ページ内にPR・広告が含まれる場合があります。
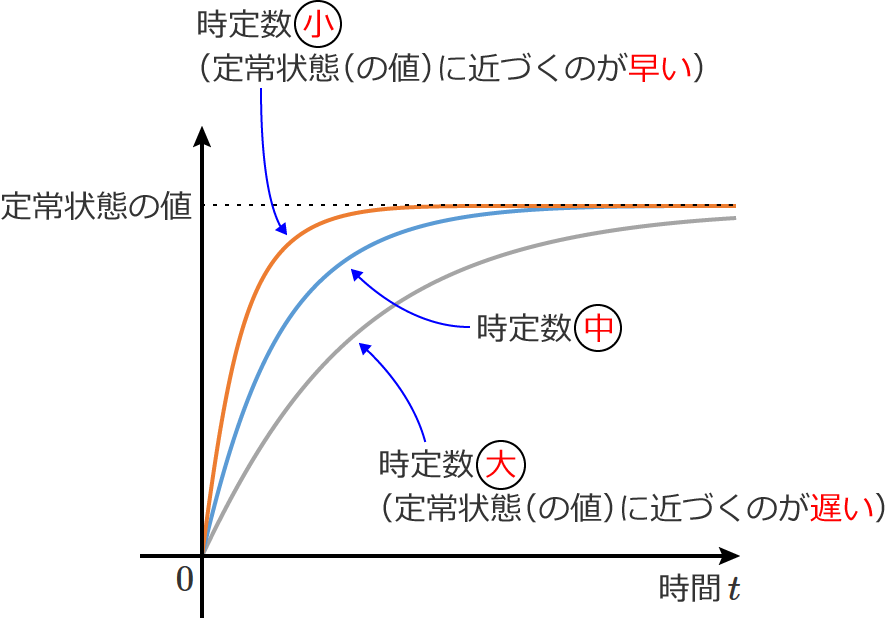
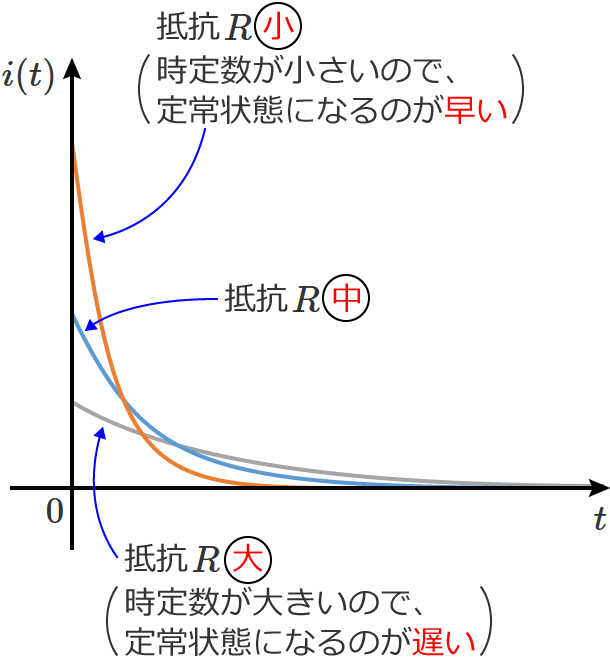
時定数は過渡状態での変化の速さを表わす量で、時定数が小さければ変化する速さは速くなり、時定数が大きければ変化する速さは遅くなります。
したがって、時定数が小さい場合は早く定常状態に近づきますが、時定数が大きい場合はゆるやかに定常状態に近づきます。
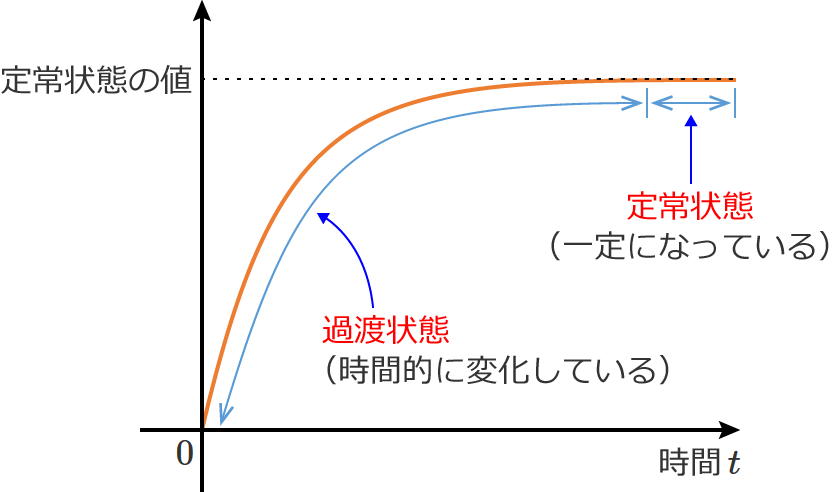
ちなみに、時間的に変化している間の状態を過渡状態、時間が十分に経過して一定の状態になっている状態を定常状態といいます。
スポンサーリンク
RL直列回路の時定数
RL直列回路の時定数と回路素子の値との関係
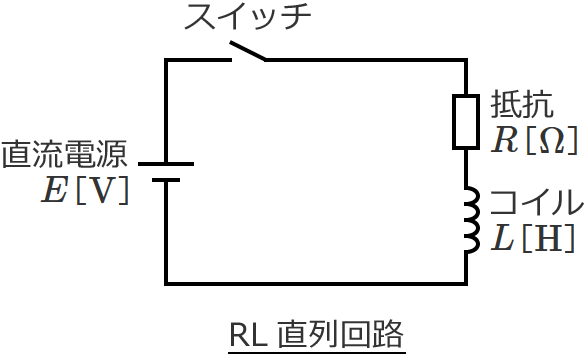
次のように、抵抗 $R$、コイル $L$、直流電源、スイッチからなるRL直列回路があるとします。
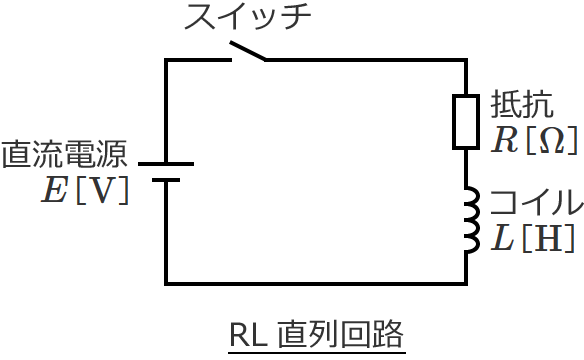
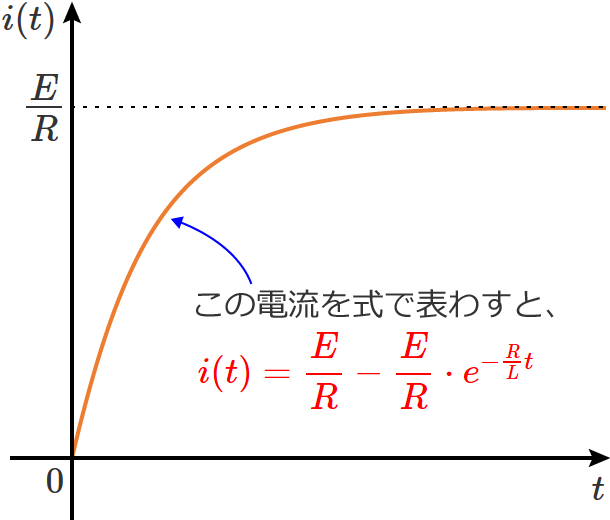
この回路のスイッチを $t=0$ でONしてRL直列回路に直流電圧を加えると、電流は次のように変化します。
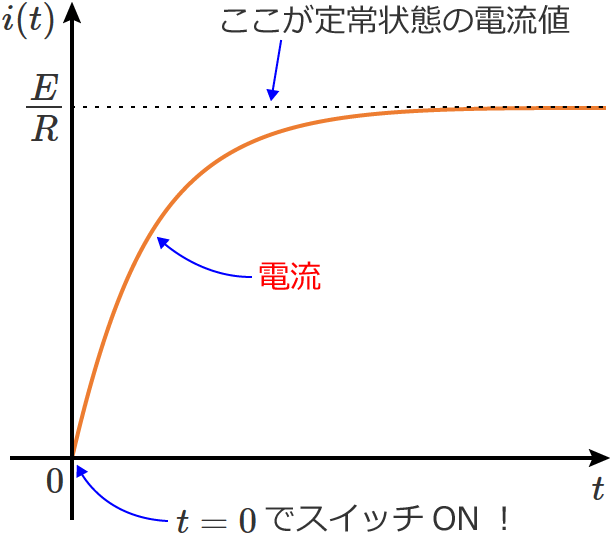
このとき、この曲線の $t=0$ における接線を引くと、接線は、定常状態の電流値( $i(t)=E/R$ の直線)と「ある時間」のところで交わります。
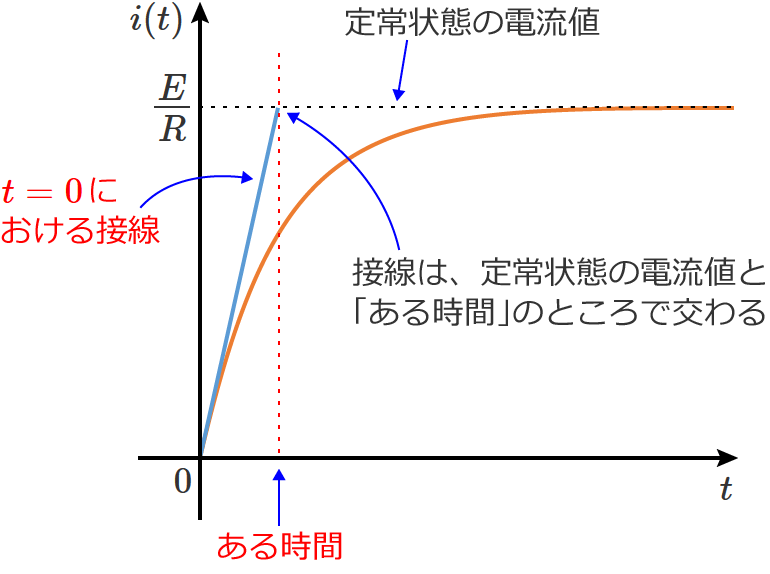
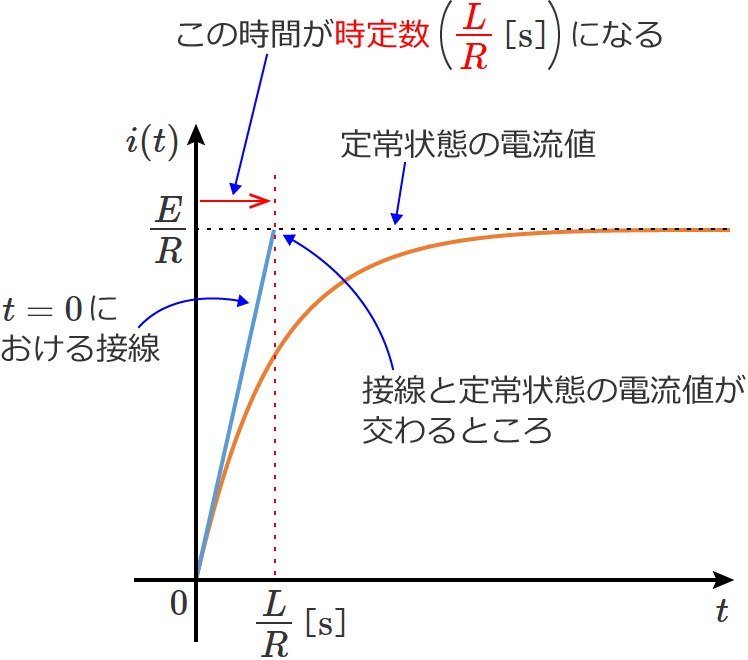
この「ある時間」が時定数になり、RL直列回路の時定数 $\tau$ は、
$\tau =\dfrac{L}{R}$ …① (これがRL直列回路の時定数)
になります。ちなみに、時定数の単位は時間の単位[$\mathrm{s}$](秒)です。
時定数の単位が時間[$\mathrm{s}$]になる理由については、こちらの時定数の単位はなぜ時間s(秒)になるのか?のページを参考にしてみてください。
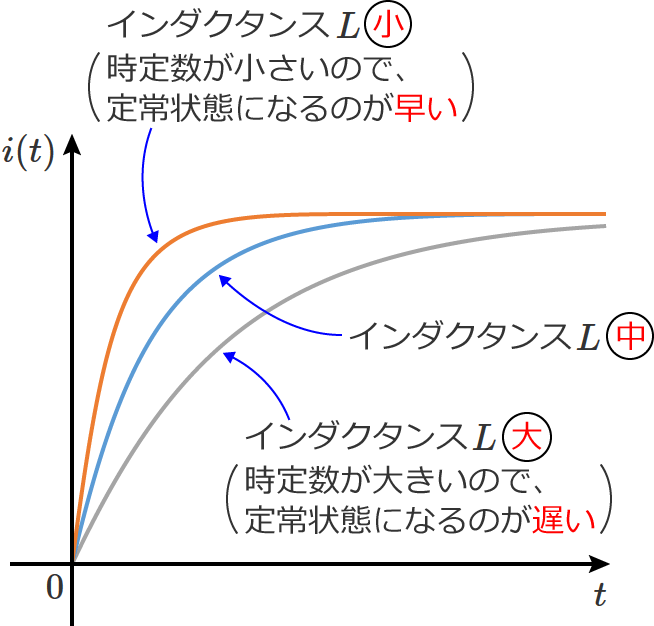
①式をみると分かるように、RL直列回路では、コイルのインダクタンス $L$ の値が大きくなると時定数は大きくなり、抵抗 $R$ の値が大きくなると時定数は小さくなります。(RL直列回路の時定数は、$L$ に比例し、$R$ に反比例します。)
つまり、RL直列回路のコイルのインダクタンス $L$ の値を大きくすると、時定数が大きくなるので定常状態になるまでの時間は遅くなり(定常状態になるまで時間がかかる)、
抵抗 $R$ の値を大きくすると、時定数が小さくなるので定常状態になるまでの時間が早くなります。
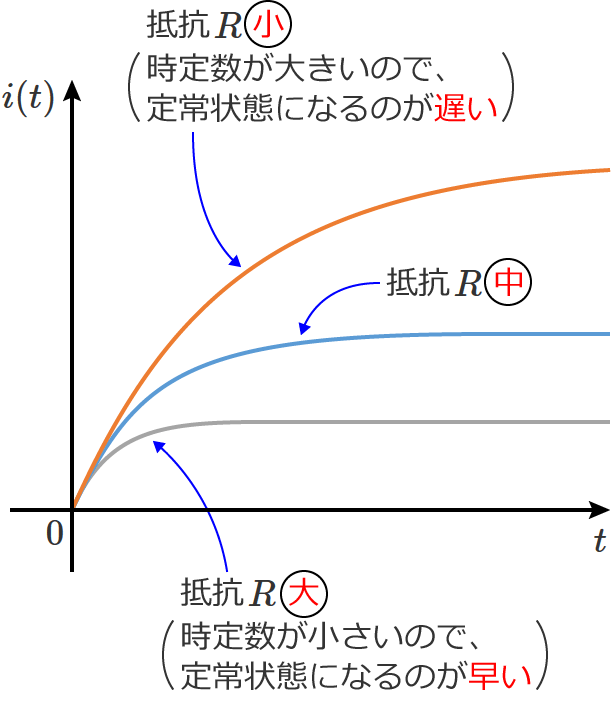
RL直列回路の時定数と電流値との関係
RL直列回路のスイッチをONして時定数と等しい時間がたつと、回路に流れる電流は、定常状態の電流値の $63.2$% になります。
この $63.2$% は、抵抗 $R$ やコイルのインダクタンス $L$ の大きさによらず、常に $63.2$% になります。
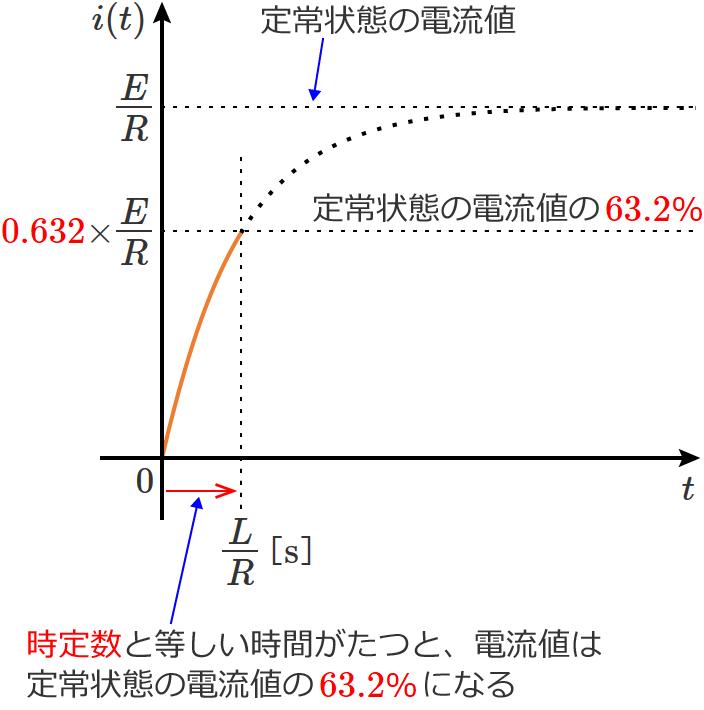
$63.2$% は 約$63.2$% です。
なぜ $63.2$% になるのかは、ちょっと計算してみると分かります。
スイッチをONしてから電流が定常状態になるまでの式は、次の図中の②式で表わされます。
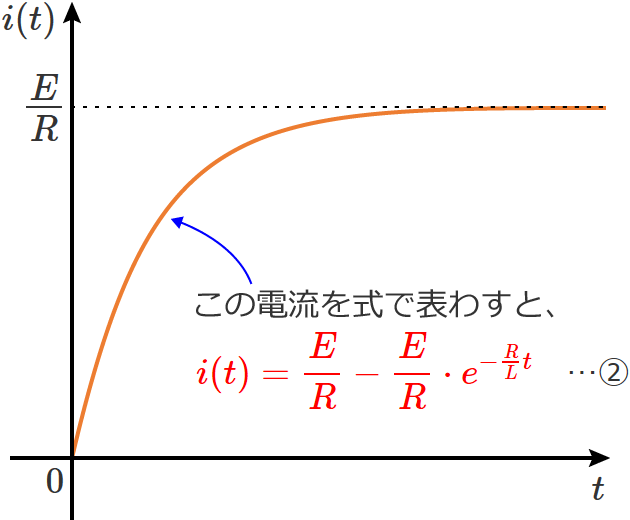
この②式の $t$ に $t=L/R$(時定数 $\tau$ )を代入すると、$t=L/R$(時定数 $\tau$ )での電流値が求められます。
では、②式に $t=L/R$ を代入してみます。すると、
$i\left(\dfrac{L}{R}\right) =\dfrac{E}{R} -\dfrac{E}{R}\cdot e^{-\frac{R}{L}\times\frac{L}{R}}$ ($t=L/R$ を代入)
$=\dfrac{E}{R} -\dfrac{E}{R}\cdot e^{-1}$
$=\dfrac{E}{R}\left( 1-e^{-1}\right)$
$\therefore i\left(\dfrac{L}{R}\right) =\dfrac{E}{R}\left( 1-\dfrac{1}{e}\right)$ …③
となり、あら不思議、③式の右辺の括弧の中には $R$ と $L$ はありません!( $t=L/R$ を代入するところで、$R/L$ の逆数の $L/R$ をかけているからこうなるんです。)

計算を続けると、③式の $e$ は自然対数の底で $e=2.71828\ldots$ という値なのでこれも代入すると、
$i\left(\dfrac{L}{R}\right) \fallingdotseq\dfrac{E}{R}\left( 1-\dfrac{1}{2.71828}\right)$
$=\dfrac{E}{R}\left(\dfrac{2.71828-1}{2.71828}\right)$
$\therefore i\left(\dfrac{L}{R}\right) \fallingdotseq\dfrac{E}{R}\times$$0.632$ …④ (これが $t=L/R$(時定数 $\tau$ )のときの電流値)
となり、$t=L/R$ のときの電流値が求められました。
この④式をみると、④式は定常状態での電流値を $0.632$倍 したものになっていて、この「$0.632$」は抵抗 $R$ やインダクタンス $L$ の大きさによりません。

なので、時定数と等しい時間がたったときの電流値は、抵抗 $R$ やインダクタンス $L$ の大きさによらず定常状態の電流値の $63.2$% になるということになります。
逆にいえば、RL直列回路の時定数は「電流が定常状態の電流値の $63.2$% に達するまでの時間」ともいえます。(ただし、$63.2$% は 約$63.2$% なので、多少の誤差はあります。)
過渡現象の勉強をしていると $63.2$% ってよく見たり聞いたりすると思うんですが(たぶん)、$63.2$% ってこういうことだったんですね、みたいなお話でした。
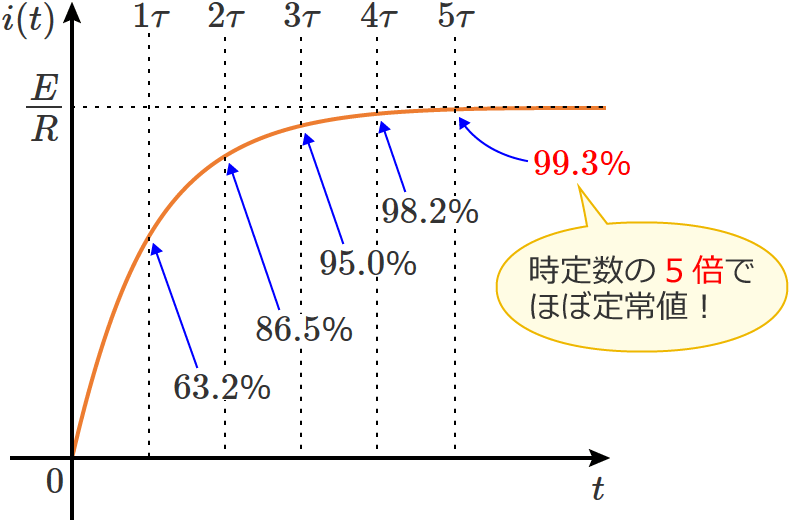
時定数の5倍程度の時間がたつとほぼ定常状態の値になる
RL直列回路でスイッチをONしてから電流が定常状態になるまでの式は、
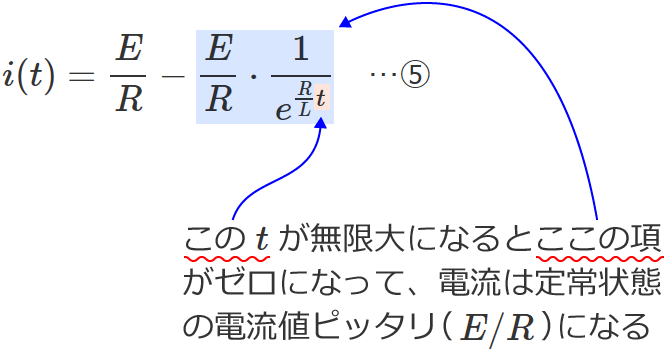
で表わされます。この式をちょっと変形すると、
$i(t)=\dfrac{E}{R} -\dfrac{E}{R}\cdot\dfrac{1}{e^{\frac{R}{L} t}}$ …⑤
となります。この⑤式をみると分かるように、電流が定常状態の値( $E/R$ )ピッタリになるためには、無限大の時間がかかります!(理論上)
例えば、実験やらなにやらで実際の回路の定常状態の値を知りたいときに、無限大の時間…、そんな時間待ってられないです。
では、どのくらいの時間待てばおおよそ定常状態の値になるのか?(おおよそです) 時定数を基準にして計算してみます。
時定数の1倍の場合
時定数の $1$倍 の時間( $1\times\tau$ )がたった場合、つまり時定数と同じ時間がたった場合は、
$i\left(\dfrac{L}{R}\right) =\dfrac{E}{R} -\dfrac{E}{R}\cdot e^{-\frac{R}{L}\times\frac{L}{R}}$
$=\dfrac{E}{R} -\dfrac{E}{R}\cdot e^{-1}$
$=\dfrac{E}{R}\left( 1-e^{-1}\right)$
$=\dfrac{E}{R}\left( 1-\dfrac{1}{e}\right)$
$\fallingdotseq\dfrac{E}{R}\left( 1-\dfrac{1}{2.71828}\right)$ ($e=2.71828$ を代入)
$\fallingdotseq\dfrac{E}{R}\times$$0.632$
となります。なので、時定数の $1$倍 の時間がたつと、電流は定常状態の値の $63.2$%( $0.632$倍 )になります。(これは、さきほど計算したものと同じです。)
時定数の2倍の場合
時定数の $2$倍 の時間( $2\times\tau$ )がたった場合は、
$i\left(\dfrac{2L}{R}\right) =\dfrac{E}{R} -\dfrac{E}{R}\cdot e^{-\frac{R}{L}\times\frac{2L}{R}}$
$=\dfrac{E}{R} -\dfrac{E}{R}\cdot e^{-2}$
$=\dfrac{E}{R}\left( 1-e^{-2}\right)$
$=\dfrac{E}{R}\left( 1-\dfrac{1}{e^2}\right)$
$\fallingdotseq\dfrac{E}{R}\left( 1-\dfrac{1}{2.71828^2}\right)$ ($e=2.71828$ を代入)
$\fallingdotseq\dfrac{E}{R}\times$$0.865$
となります。なので、時定数の $2$倍 の時間がたつと、電流は定常状態の値の $86.5$%( $0.865$倍 )になります。
時定数の3倍の場合
時定数の $3$倍 の時間( $3\times\tau$ )がたった場合は、
$i\left(\dfrac{3L}{R}\right) =\dfrac{E}{R} -\dfrac{E}{R}\cdot e^{-\frac{R}{L}\times\frac{3L}{R}}$
$=\dfrac{E}{R} -\dfrac{E}{R}\cdot e^{-3}$
$=\dfrac{E}{R}\left( 1-e^{-3}\right)$
$=\dfrac{E}{R}\left( 1-\dfrac{1}{e^3}\right)$
$\fallingdotseq\dfrac{E}{R}\left( 1-\dfrac{1}{2.71828^3}\right)$ ($e=2.71828$ を代入)
$\fallingdotseq\dfrac{E}{R}\times$$0.950$
となります。なので、時定数の $3$倍 の時間がたつと、電流は定常状態の値の $95.0$%( $0.950$倍 )になります。(だんだん定常状態の値に近づいてきました!)
時定数の4倍の場合
時定数の $4$倍 の時間( $4\times\tau$ )がたった場合は、
$i\left(\dfrac{4L}{R}\right) =\dfrac{E}{R} -\dfrac{E}{R}\cdot e^{-\frac{R}{L}\times\frac{4L}{R}}$
$=\dfrac{E}{R} -\dfrac{E}{R}\cdot e^{-4}$
$=\dfrac{E}{R}\left( 1-e^{-4}\right)$
$=\dfrac{E}{R}\left( 1-\dfrac{1}{e^4}\right)$
$\fallingdotseq\dfrac{E}{R}\left( 1-\dfrac{1}{2.71828^4}\right)$ ($e=2.71828$ を代入)
$\fallingdotseq\dfrac{E}{R}\times$$0.982$
となります。なので、時定数の $4$倍 の時間がたつと、電流は定常状態の値の $98.2$%( $0.982$倍 )になります。
時定数の5倍の場合
時定数の $5$倍 の時間( $5\times\tau$ )がたった場合は、
$i\left(\dfrac{5L}{R}\right) =\dfrac{E}{R} -\dfrac{E}{R}\cdot e^{-\frac{R}{L}\times\frac{5L}{R}}$
$=\dfrac{E}{R} -\dfrac{E}{R}\cdot e^{-5}$
$=\dfrac{E}{R}\left( 1-e^{-5}\right)$
$=\dfrac{E}{R}\left( 1-\dfrac{1}{e^5}\right)$
$\fallingdotseq\dfrac{E}{R}\left( 1-\dfrac{1}{2.71828^5}\right)$ ($e=2.71828$ を代入)
$\fallingdotseq\dfrac{E}{R}\times$$0.993$
となります。なので、時定数の $5$倍 の時間がたつと、電流は定常状態の値の $99.3$%( $0.993$倍 )になります。( $5$倍 ならけっこういいかんじ。)
以上より、時定数の $5$倍 の時間がたつと電流は定常状態の値の $99.3$% になるので、時定数の $5$倍 くらいの時間待てばほぼ定常状態の値!といって良さそうです。
スポンサーリンク
スポンサーリンク
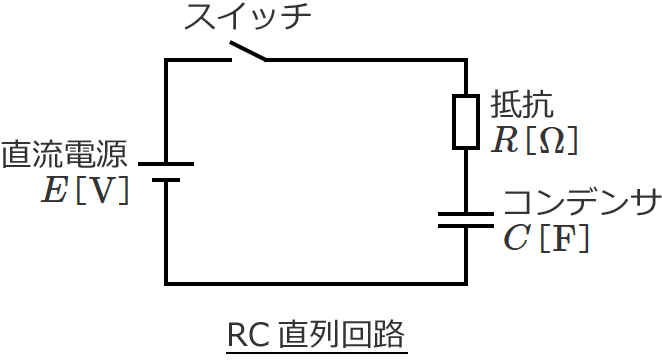
RC直列回路の時定数
次は、RC直列回路についてです。RL直列回路とほぼ同じような内容なんですが、いちおう…、ね。
RC直列回路の時定数と回路素子の値との関係
次のように、抵抗 $R$、コンデンサ $C$、直流電源、スイッチからなるRC直列回路があるとします。(スイッチを入れる前のコンデンサ $C$ に蓄えられている電荷(初期電荷)はゼロとします。)
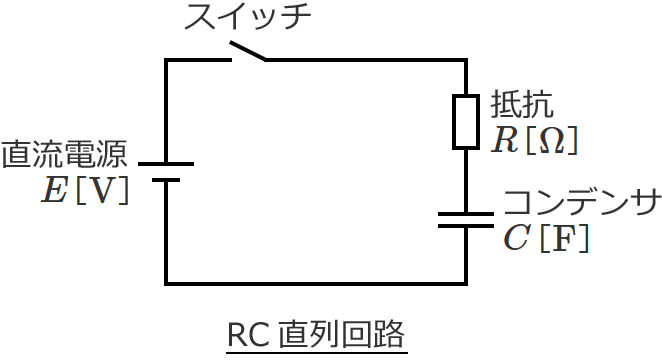
この回路のスイッチを $t=0$ でONしてRC直列回路に直流電圧を加えると、電流は次のように変化します。
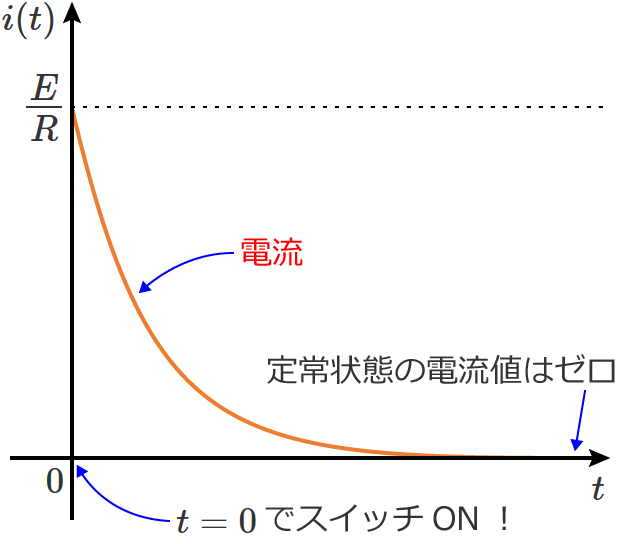
このとき、この曲線の $t=0$ における接線を引くと、接線は、定常状態の電流値( $i(t)=0$ の直線)と「ある時間」のところで交わります。
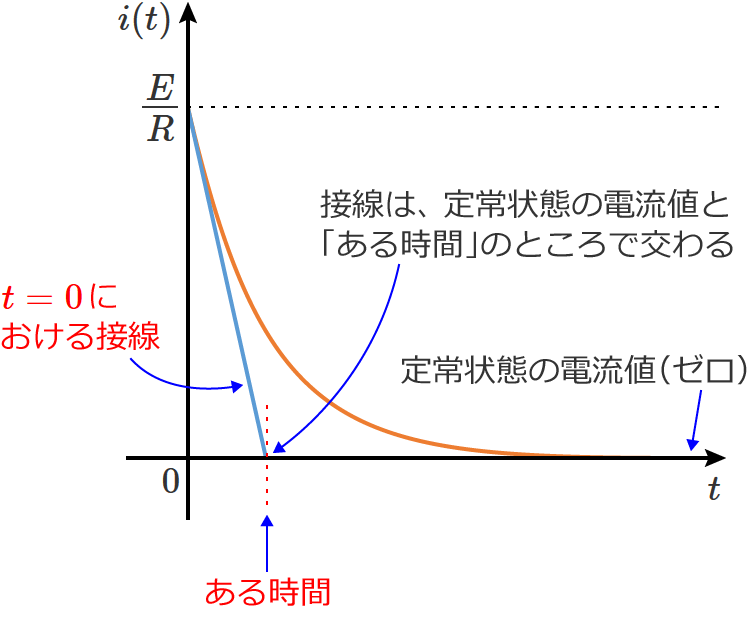
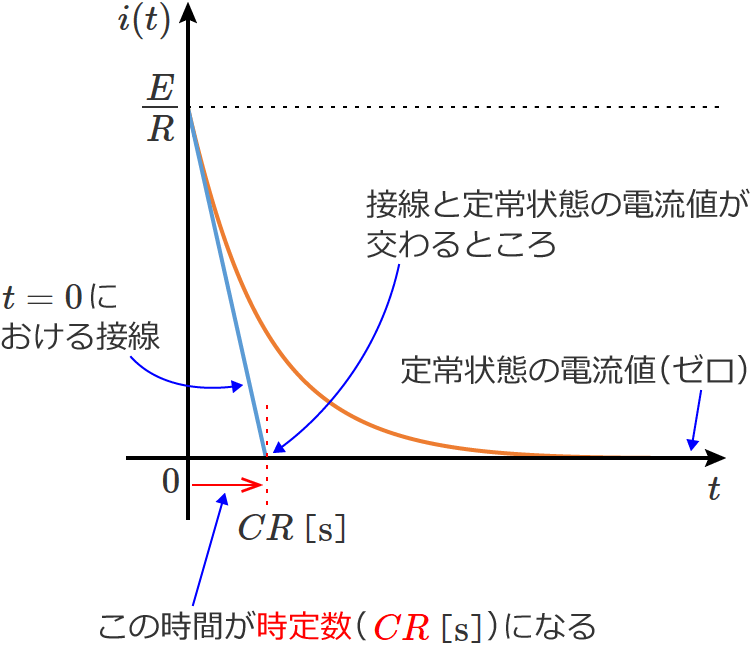
この「ある時間」が時定数になり、RC直列回路の時定数 $\tau$ は、
$\tau =CR$ …⑥ (これがRC直列回路の時定数)
になります。
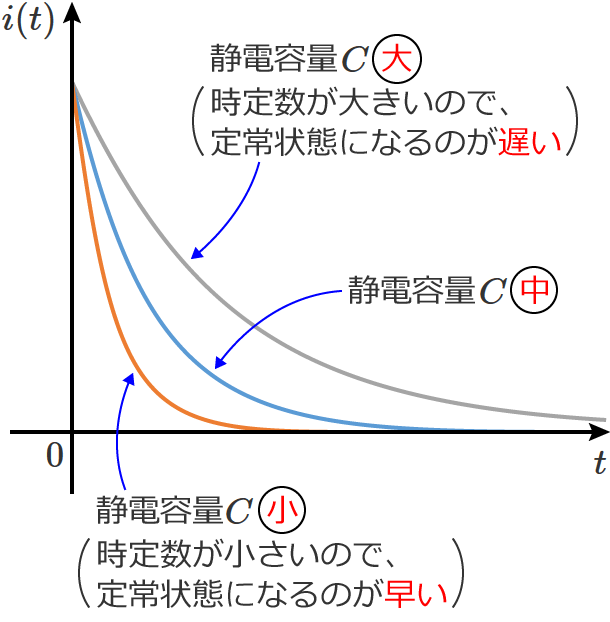
⑥式をみると分かるように、RC直列回路では、コンデンサの静電容量 $C$ の値または抵抗 $R$ の値が大きくなると時定数は大きくなります。(RC直列回路の時定数は、$C$ と $R$ に比例します。)
つまり、RC直列回路のコンデンサの静電容量 $C$ の値または抵抗 $R$ の値を大きくすると、時定数が大きくなるので定常状態になるまでの時間は遅くなります(定常状態になるまで時間がかかる)。
RC直列回路の時定数と電流値との関係
RC直列回路のスイッチをONして時定数と等しい時間がたつと、回路に流れる電流は、最初の電流値( $E/R$ )の $36.8$% になります。(最初の電流値の $36.8$% の値は、最初の電流値から $63.2$% 減少した値になります。)
この $36.8$% は、抵抗 $R$ やコンデンサの静電容量 $C$ の大きさによらず、常に $36.8$% になります。
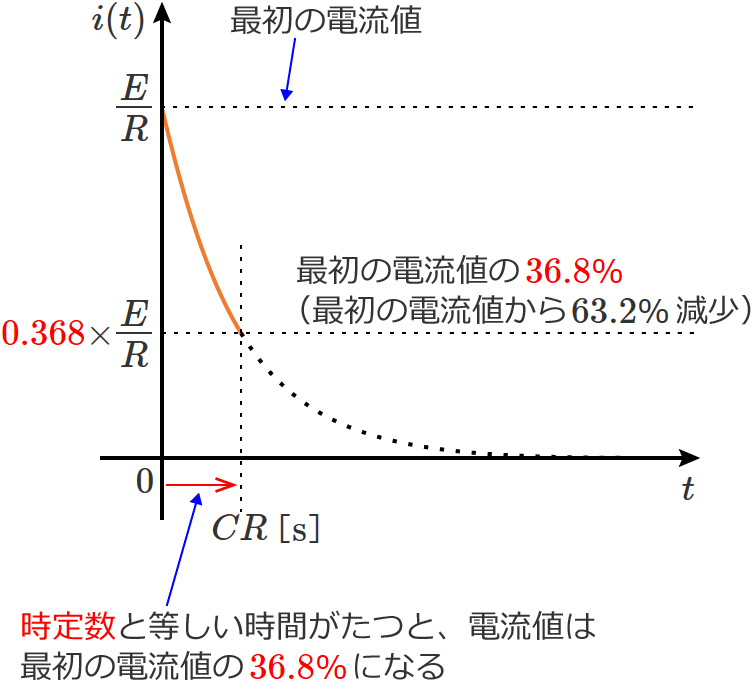
$36.8$% は 約$36.8$% です。
なぜ $36.8$% になるのかは、さきほどのRL直列回路の場合と同じように計算してみると分かります。
スイッチをONしてから電流が定常状態になるまでの式は、次の図中の⑦式で表わされます。
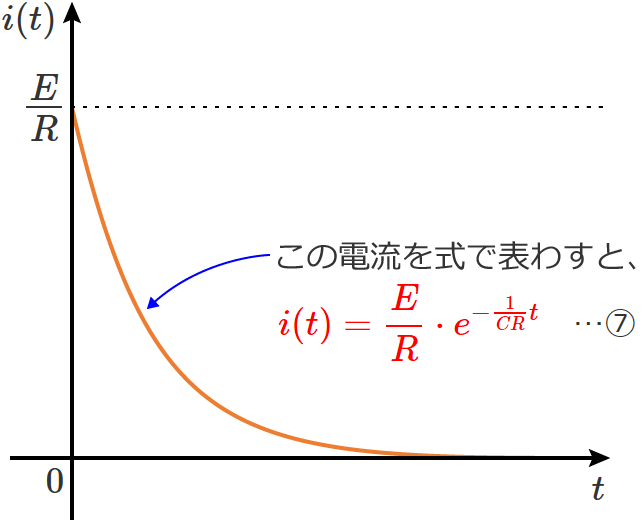
この⑦式の $t$ に $t=CR$(時定数 $\tau$ )を代入すると、$t=CR$(時定数 $\tau$ )での電流値が求められます。
では、⑦式に $t=CR$ を代入してみます。すると、
$i(CR)=\dfrac{E}{R}\cdot e^{-\frac{1}{CR}\times CR}$ ($t=CR$ を代入)
$=\dfrac{E}{R}\cdot e^{-1}$
$=\dfrac{E}{R}\cdot\dfrac{1}{e}$
$\fallingdotseq\dfrac{E}{R}\cdot\dfrac{1}{2.71828}$ ($e=2.71828$ を代入)
$\therefore i(CR)\fallingdotseq\dfrac{E}{R}\times$$0.368$ …⑧ (これが $t=CR$(時定数 $\tau$ )のときの電流値)
となり、$t=CR$ のときの電流値が求められました。
この⑧式をみると、⑧式は最初の電流値を $0.368$倍 したものになっていて、この「$0.368$」は抵抗 $R$ や静電容量 $C$ の大きさによりません。
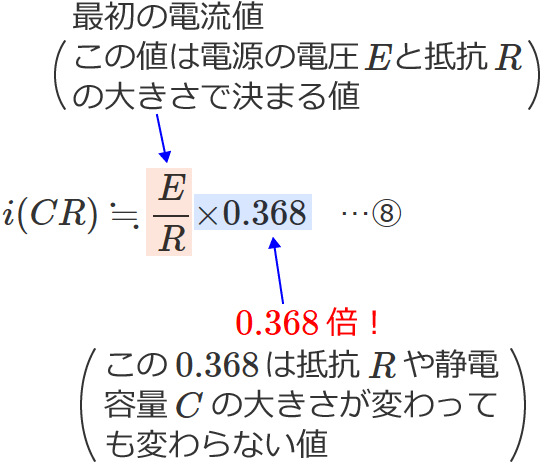
なので、時定数と等しい時間がたったときの電流値は、抵抗 $R$ や静電容量 $C$ の大きさによらず最初の電流値の $36.8$% になるということになります。
逆にいえば、RC直列回路の時定数は「最初の電流値が $36.8$% に減少するまでの時間」ともいえます。(ただし、$36.8$% は 約$36.8$% なので、多少の誤差はあります。)
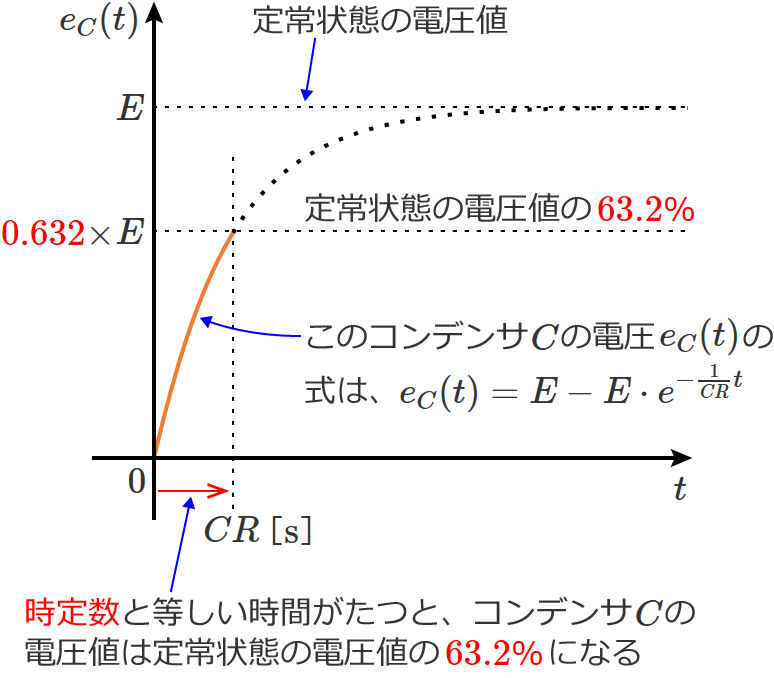
ちなみに、ここではRC直列回路の電流についてですが、RC直列回路のコンデンサ $C$ の電圧で考える場合は「定常状態の電圧値の $63.2$% に達するまでの時間」が時定数になります。
- 時定数は過渡状態での変化の速さを表わす量
- 時定数が小さければ早く定常状態に近づく
- 時定数が大きければゆるやかに定常状態に近づく
- RL直列回路の時定数は $\tau =L/R$
- RC直列回路の時定数は $\tau =CR$
スポンサーリンク
スポンサーリンク
過渡現象については、こちらの過渡現象とはのページを参考にしてみてください。
RL直列回路の時定数( $\tau =L/R$ )の求め方については、こちらのRL直列回路の時定数の導出のページを参考にしてみてください。
RC直列回路の時定数( $\tau =CR$ )の求め方については、こちらのRC直列回路の時定数の導出のページを参考にしてみてください。
過渡現象とは ←BACK
NEXT→ 時定数の単位はなぜ時間s(秒)になるのか?
スポンサーリンク
時定数 関連ページ
- 過渡現象とは
- 過渡現象について解説しています。過渡現象とは、ある定常状態から別の定常状態に移るまでに起こる現象(電圧や電流などの時間的な変化)のことをいい、過渡現象は回路の状態が変化することによって起こります。
- 時定数の単位はなぜ時間s(秒)になるのか?
- 過渡現象の時定数の単位はなぜ時間s(秒)になるのか?について解説しています。時定数の単位が時間(s)になる過程も詳しく書いていますので、参考にしてみてください。
- RL直列回路の時定数(τ=L/R)の導出
- RL直列回路の時定数(τ=L/R)の導出方法について解説しています。RL直列回路の時定数は、電流のt=0における接線と定常状態の電流を表わす直線との交点の時間を算出すると求められます。
- RC直列回路の時定数(τ=CR)の導出
- RC直列回路の時定数(τ=CR)の導出方法について解説しています。RC直列回路の時定数は、電流のt=0における接線と定常状態の電流を表わす直線との交点の時間を算出すると求められます。
- RL直列回路の過渡現象の解き方
- RL直列回路の過渡現象の解き方について解説しています。過渡現象を解くためには微分方程式を解く必要があるため計算がちょっと大変ですが、解き方のパターンをおぼえてしまうとそれほど難しくはありませんよ。
- RC直列回路の過渡現象の解き方
- RC直列回路の過渡現象の解き方について解説しています。RC直列回路の過渡現象はRL直列回路よりもちょっとだけ計算が大変ですが、解き方のパターンは同じなので、おぼえてしまうとそれほど難しくはありませんよ。
- ラプラス変換によるRL直列回路の過渡現象の解き方
- ラプラス変換によるRL直列回路の過渡現象の解き方について解説しています。ラプラス変換を使ってRL直列回路の過渡現象を解いていますので、ラプラス変換を使った過渡現象の解き方の参考にしてみてください。
- ラプラス変換によるRC直列回路の過渡現象の解き方
- ラプラス変換によるRC直列回路の過渡現象の解き方について解説しています。ラプラス変換を使ってRC直列回路の過渡現象を解いていますので、ラプラス変換を使った過渡現象の解き方の参考にしてみてください。


