スポンサーリンク
RC直列回路の過渡現象の解き方
※ページ内にPR・広告が含まれる場合があります。
RC直列回路に流れる電流の求め方
次の図のように、抵抗 $R$[$\Omega$]、コンデンサ $C$[$\mathrm{F}$]、直流電源 $E$[$\mathrm{V}$]、スイッチ $\mathrm{S}$ からなるRC直列回路があるとします。(スイッチ $\mathrm{S}$ を入れる前のコンデンサ $C$ に蓄えられている電荷はゼロとします。(つまり、コンデンサの初期電荷はなく、$t=0$ で $q(0) = 0$ ))
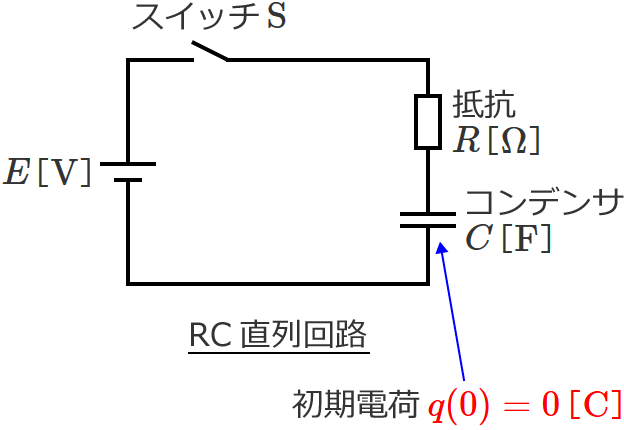
この回路のスイッチをONすると過渡現象が起こるため、スイッチをONすると回路に流れる電流は時間的に変化し、その後ある程度の時間が経過すると一定値に落ち着きます。
このような時間的に変化する過渡現象の電圧や電流を求めるときは、次のような手順で解いていきます。
回路の過渡現象を解く基本的な手順
❶対象の回路の回路方程式(微分や積分が含まれる)をたてる
❷初期条件を考慮して❶の微分方程式(または積分方程式)を解く
ざっくりいえばこれだけですが、上に記載した解く手順❷の「微分方程式(または積分方程式)を解く」ことが回路によっては大変になったりします。
それでは、RC直列回路に流れる電流を求めてみます。
スポンサーリンク
まず初めに、回路の回路方程式をたてます。
回路に流れる電流を $i(t)$[$ \mathrm{A} $]として、
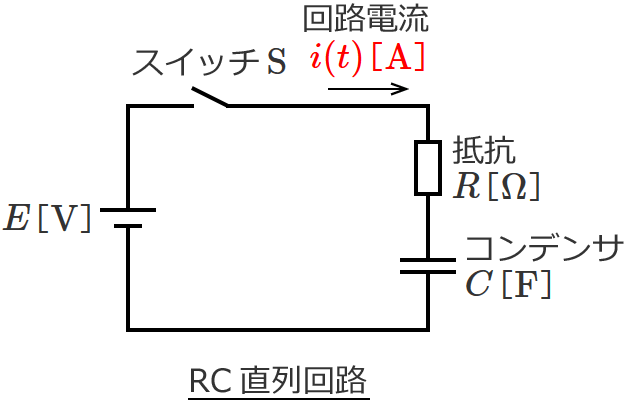
この回路にキルヒホッフの第二法則(電圧則)を適用すれば、回路方程式は次の①式(積分方程式)で与えられます。
$E = R \, i(t) + \dfrac{1}{C} \displaystyle\int i(t) \, dt$ …①
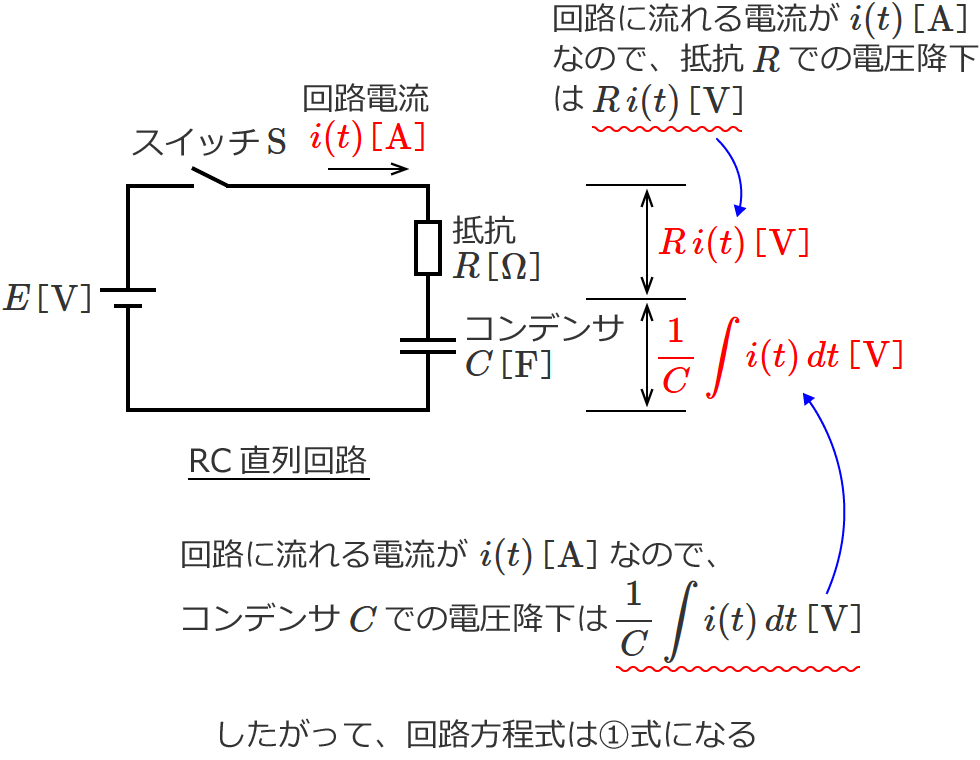
ここでちょっと補足ですが、コンデンサ $C$ の電圧降下の式は次のようにして求めます。
コンデンサ $C$ に蓄えられる電荷を $q(t)$[$ \mathrm{C} $]とすると、電流と電荷の関係は次の式で与えられます。
$i(t) = \dfrac{d \, q(t)}{dt}$ (この式の意味は、電荷 $q(t)$ を微分すると電流になりますよ、という意味ですね。)
上式の両辺を $t$ で積分します。すると、
$\displaystyle\int i(t) \, dt = \int \left( \dfrac{d \, q(t)}{dt} \right) \, dt$
$\displaystyle\int i(t) \, dt = q(t)$
$\therefore q(t) = \displaystyle\int i(t) \, dt$ となります。 (この式の意味は、電流を積分すると電荷になりますよ、という意味ですね。)
あとはコンデンサの公式( $Q = CV$ )にあてはめるだけです。コンデンサ $C$ の電圧降下を $e_C(t)$ とすると、
$q(t) = C \cdot e_C(t)$
$\displaystyle\int i(t) \, dt = C \cdot e_C(t)$
$e_C(t) = \dfrac{1}{C} \displaystyle\int i(t) \, dt$
したがって、コンデンサの電圧降下 $e_C(t)$ は、
$\therefore e_C(t) = \dfrac{1}{C} \displaystyle\int i(t) \, dt$ となります。
それでは、話を回路方程式(①式)に戻します。
①の回路方程式がたてられたので、あとは①式を解くだけなのですが、①式は積分の形で与えられています。これを計算しやすくするため、さきほどの電流と電荷の関係式を使って微分の形にもっていきます。
電流と電荷の関係式より、次の2つの式が成り立ちますね。
$i(t) = \dfrac{d \, q(t)}{dt}$
$\displaystyle\int i(t) \, dt = q(t)$
これらを①式に代入します。すると、
$E = R \dfrac{d \, q(t)}{dt} + \dfrac{1}{C} q(t)$ …② となります。
②式は電流の式ではなく電荷の式になっていますが、②式を電荷 $q(t)$ について解いて、電流と電荷の関係式を使って電流 $i(t)$ の式にすれば電流 $i(t)$ を求めることができます。
では、②式の微分方程式を電荷 $q(t)$ について解いていきましょう。
微分方程式は、その方程式の形で色々な解き方があったり、ラプラス変換を使って解いたりすることができますが、ここでは微分方程式の解法の一つである変数分離法を使って解くことにします。
変数分離法は名前の通り、変数を左辺と右辺に分離して解いていく方法です。
②式の場合、電荷 $q(t)$ と時間 $t$ が変数なので、電荷 $q(t)$ に関するものは左辺に、時間 $t$ に関するものは右辺になるように②式を変形します。(電源電圧 $E$ と抵抗 $R$ とコンデンサの静電容量 $C$ は定数なので、左辺と右辺どちらにあってもいいです。)
②式の $R \dfrac{d \, q(t)}{dt}$ を左辺に、$E$ を右辺に移動します。すると、
$R \dfrac{d \, q(t)}{dt} = E - \dfrac{1}{C} q(t)$
$R \dfrac{d \, q(t)}{dt} = \dfrac{CE - q(t)}{C}$
上式の両辺を $R$ で割ります。
$\dfrac{d \, q(t)}{dt} = \dfrac{CE - q(t)}{CR}$
両辺を $CE - q(t)$ で割ります。
$\dfrac{1}{CE - q(t)} \cdot \dfrac{d \, q(t)}{dt} = \dfrac{1}{CR}$
両辺に $dt$ をかけます。
$\dfrac{1}{CE - q(t)} \cdot d \, q(t) = \dfrac{1}{CR} \cdot dt$
計算をしやすくするため、もうちょっと変形しておきます。両辺にマイナスをかけて、
$\dfrac{1}{q(t) - CE} \cdot d \, q(t) = -\dfrac{1}{CR} \cdot dt$
$\therefore \dfrac{1}{q(t) - CE} \cdot d \, q(t) = -\dfrac{1}{CR} \cdot dt$ …③
これで左辺は電荷 $q(t)$(変数)に関するもの、右辺は時間 $t$(変数)に関するものとなり、2つの変数を左辺と右辺に分離することができました。(定数は変数ではないので、左辺にあっても右辺にあってもいいです。)
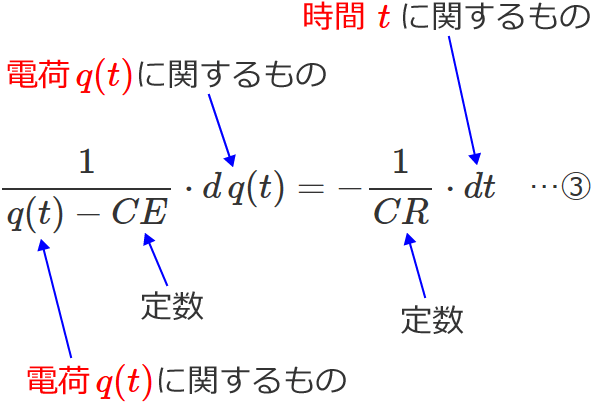
変数を分離できたので、あとは両辺を積分して計算を続けていきます。
③式の両辺を積分すると(両辺に積分記号を付けるだけ)、
$\displaystyle\int \dfrac{1}{q(t) - CE} \, d \, q(t) = -\int \dfrac{1}{CR} \, dt$ …④
となります。では、④式の左辺から計算してみましょう。
④式の左辺は $\displaystyle\int \dfrac{1}{x} \, dx$ の形の積分なので、積分の公式より、
④式の左辺 $ = \displaystyle\int \dfrac{1}{q(t) - CE} \, d \, q(t)$
$= \log_e \left| q(t) - CE \right| + A$ ( $A$ は積分定数) …⑤
⑤式に絶対値が付いているので、これを外しましょう。
絶対値の中は $q(t) - CE$ ですが、$q(t)$ はコンデンサ $C$ に蓄えられていく電荷で、$CE$ は電源電圧 $E$ がコンデンサ $C$ にすべてかかっている状態(つまり、定常状態)での電荷なので、$q(t) \leqq CE$ となり、絶対値の中は常にゼロ以下になります。
なので、絶対値の中( $q(t)-CE$ )にマイナスをかけると絶対値を外すことができます。つまり、
$\log_e \left| q(t) - CE \right| + A$ $= \log_e \left( CE - q(t) \right) +A$ …⑥
となります。したがって⑤式と⑥式より、
④式の左辺 $ = \log_e \left( CE - q(t) \right) + A$ …⑦ となります。これで④式の左辺は計算できたので、次は④式の右辺について考えます。
$\dfrac{1}{CR}$ は定数なので、そのまま積分の外に出します。すると、
④式の右辺 $ = -\displaystyle\int \dfrac{1}{CR} \, dt$
$= -\dfrac{1}{CR} \displaystyle\int \, dt$
$= -\dfrac{1}{CR} \cdot t + B$ ( $B$ は積分定数) …⑧
となります。
以上で④式の左辺と右辺が計算できたので、⑦、⑧式を④式に戻すと次の⑨式になります。
$\log_e \left( CE - q(t) \right) + A$ $= -\dfrac{1}{CR} \cdot t + B$ …⑨
⑨式には $A$ と $B$ の2つの積分定数があるので、積分定数を $D$ として1つにまとめてしまいます。(つまり、$B-A=D$ とおく)
$\log_e \left( CE - q(t) \right) = -\dfrac{1}{CR} \cdot t + D$
対数の定義より、この式を展開すると、
$CE - q(t) = e^{-\frac{1}{CR} t +D}$
$CE - q(t) = e^{-\frac{1}{CR} t} \cdot e^D$
$\therefore CE - q(t) = e^D \cdot e^{-\frac{1}{CR} t}$ …⑩
あとは、⑩式の中の積分定数を求めます。積分定数は回路の初期条件を⑩式に代入すれば求められ、この回路の場合、時間 $t = 0$ のときはコンデンサ $C$ に蓄えられている電荷がゼロなので、初期条件は $t = 0$、$q(t) = 0$ になります。(電荷の式で考えているので、初期条件も電流ではなく電荷で考えます。)
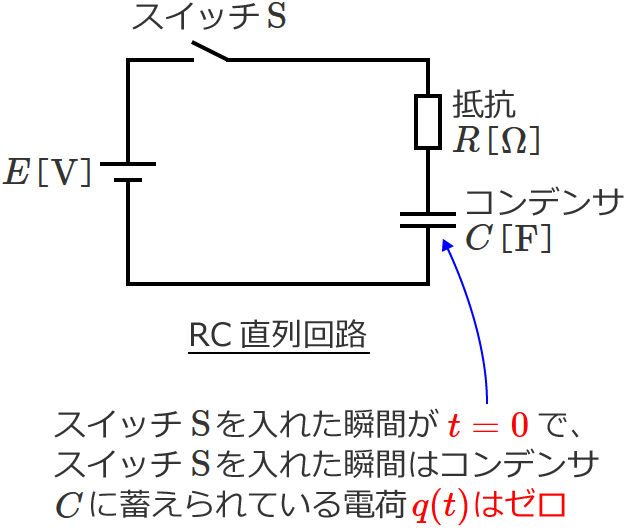
$t=0$、$q(t) = 0$ を⑩式に代入すると、
$CE - 0 = e^D \cdot e^{-\frac{1}{CR} \times 0}$
$CE = e^D \cdot e^0 = e^D \cdot 1 = e^D$
$\therefore e^D = CE$ …⑪
⑪式の両辺の対数をとって $D = \cdots$ を求めてもいいのですが、⑩式をみると $e^D$ をそのまま代入できるので、⑪を⑩式にそのまま代入します。すると、
$CE - q(t) = CE \cdot e^{-\frac{1}{CR} t}$
$-q(t) = -CE + CE \cdot e^{-\frac{1}{CR} t}$
$\therefore q(t) = CE - CE \cdot e^{-\frac{1}{CR} t}$ …⑫ (これがコンデンサ $C$ の電荷)
となり、RC直列回路のコンデンサ $C$ に蓄えられる電荷 $q(t)$ が求められました。
ちなみに、この⑫式の右辺の第1項を定常解、第2項を過渡解といいます。
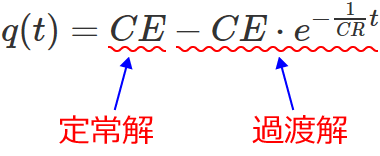
⑫式は電荷の式で、求めたいのは回路に流れる電流 $i(t)$ なので、次に、⑫式を使って電流 $i(t)$ を求めます。
電荷の式から電流の式を求めるためには、ここで何度か使っている電流と電荷の関係式を使います。
電流と電荷の関係式は、$i(t) = \dfrac{d \, q(t)}{dt}$ でしたので、⑫式の電荷 $q(t)$ を時間 $t$ で微分すれば電流 $i(t)$ が求められます。なので、
$i(t) = \dfrac{d \, q(t)}{dt}$ $= \dfrac{d}{dt} \left( CE - CE \cdot e^{-\frac{1}{CR} t} \right)$
となり、この式を解くと電流 $i(t)$ を求めることができます。では、解いてみましょう。
$CE$ は定数なので、微分の外に出してしまいます。
$i(t) = CE \cdot \dfrac{d}{dt} \left( 1 - e^{-\frac{1}{CR} t} \right)$
$=CE\left(\dfrac{d}{dt} 1-\dfrac{d}{dt} e^{-\frac{1}{CR} t} \right)$
$= CE \, \left\lbrace 0 - \left( -\dfrac{1}{CR} \cdot e^{-\frac{1}{CR} t} \right) \right\rbrace$
$= CE \left( \dfrac{1}{CR} \cdot e^{-\frac{1}{CR} t} \right)$
$= \dfrac{E}{R} \cdot e^{-\frac{1}{CR} t}$
$\therefore i(t) = \dfrac{E}{R} \cdot e^{-\frac{1}{CR} t}$ …⑬ (これが回路に流れる電流)
となり、RC直列回路に流れる電流 $i(t)$ が求められました。
RC直列回路に流れる電流のグラフ
RC直列回路に流れる電流 $i(t)$ が求められたので、次は $i(t)$ のグラフを書いてみます。
さきほど求めた電流の式(⑬式)より、RC直列回路の回路に流れる電流の式は次のようになります。
$i(t) = \dfrac{E}{R} \cdot e^{-\frac{1}{CR} t}$ …⑬
⑬式より、回路に流れる電流 $i(t)$ の $t=0$ および $t=\infty$ での値をそれぞれ求めると、
$t=0$ のとき
$i(0)=\dfrac{E}{R} \cdot e^{-\frac{1}{CR}\times 0}$ (⑬式の $t$ に $0$ を代入した)
$=\dfrac{E}{R}\cdot e^0$
$=\dfrac{E}{R}\times 1=\dfrac{E}{R}$
$\therefore t=0$ のとき $\dfrac{E}{R}$
$t=\infty$ のとき
$i(\infty)=\dfrac{E}{R} \cdot e^{-\frac{1}{CR}\times\infty}$ (⑬式の $t$ に $\infty$ を代入した)
$=\dfrac{E}{R} \cdot\dfrac{1}{e^{\frac{1}{CR}\times\infty}}$
$=\dfrac{E}{R} \cdot\dfrac{1}{\infty} =0$
$\therefore t=\infty$ のとき $0$
となります。
また、⑬式は $e^{-\frac{1}{CR} t}$ によって減衰していくので、回路に流れる電流 $i(t)$ のグラフは、時間がたつにつれて減少がゆるやかになる次のようなグラフになります。
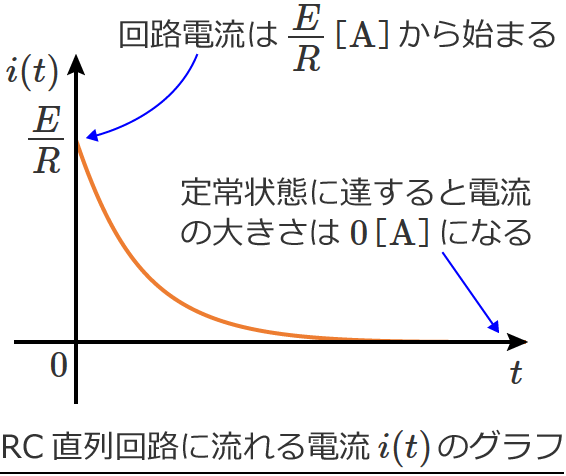
このグラフをみると、回路に流れる電流は $\dfrac{E}{R}$[$ \mathrm{A} $]から始まり、ある程度時間が経過する(定常状態に達するという意味)と電流の大きさは $0$[$ \mathrm{A} $]になるのが分かります。
つまり、スイッチをONした直後はコンデンサ $C$ は短絡されたような状態で抵抗 $R$ だけに制限された電流が流れ、回路に電流が流れたことでコンデンサ $C$ に電荷が徐々に蓄えられ、コンデンサ $C$ に電荷がたまりきる(フル充電)と回路には電流が流れなくなります(定常状態に達する)。(これ、大事!)
ちなみに、RC直列回路の時定数 $\tau$ は、$\tau = CR$ になります。
時定数については、こちらの時定数のページを参考にしてみてください。
RC直列回路のコンデンサCに蓄えられる電荷のグラフ
ついでに、コンデンサ $C$ に蓄えられる電荷のグラフも書いてみます。
コンデンサ $C$ に蓄えられる電荷の式は⑫式より、
$q(t) = CE - CE \cdot e^{-\frac{1}{CR} t}$ …⑫ でした。
⑫式より、コンデンサ $C$ に蓄えられる電荷 $q(t)$ の $t=0$ および $t=\infty$ での値をそれぞれ求めると、
$t=0$ のとき
$q(0)=CE-CE\cdot e^{-\frac{1}{CR}\times 0}$ (⑫式の $t$ に $0$ を代入した)
$=CE-CE\cdot e^0$
$=CE-CE\times 1=0$
$\therefore t=0$ のとき $0$
$t=\infty$ のとき
$q(\infty)=CE-CE\cdot e^{-\frac{1}{CR}\times\infty}$ (⑫式の $t$ に $\infty$ を代入した)
$=CE-CE\cdot\dfrac{1}{e^{\frac{1}{CR}\times\infty}}$
$=CE-CE\cdot\dfrac{1}{\infty}$
$=CE-0=CE$
$\therefore t=\infty$ のとき $CE$
となります。
また、⑫式の第2項は $e^{-\frac{1}{CR} t}$ によって減衰していくので、コンデンサ $C$ に蓄えられる電荷 $q(t)$ のグラフは、時間がたつにつれて増加がゆるやかになる次のようなグラフになります。
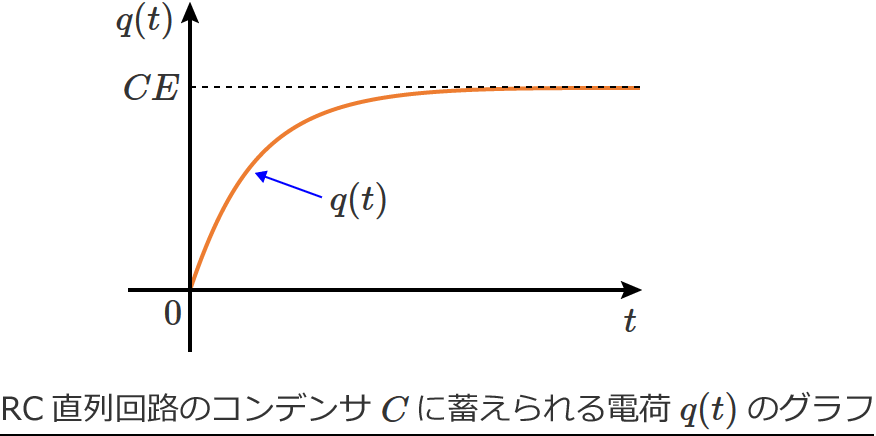
以上でRC直列回路のコンデンサ $C$ に蓄えられる電荷 $q(t)$ のグラフが書けましたが、$q(t)$ のグラフをみるとRC直列回路の場合、コンデンサ $C$ に蓄えられる電荷はゼロから始まり、徐々に大きくなって、ある程度の時間が経過する(定常状態に達するという意味)と $CE$ の大きさの電荷がたまったままになることが分かります。(つまり、定常状態に達すると電荷の大きさは変化しなくなるということです。)
ちなみに、電流と電荷の関係式より電流と電荷の関係は $i(t) = \dfrac{d \, q(t)}{dt}$ なので、電荷 $q(t)$ の大きさが変化しないということは電流が流れないということになります。(これ、大事!)
スポンサーリンク
スポンサーリンク
RC直列回路の抵抗Rの電圧の求め方
RC直列回路に流れる電流 $i(t)$ はさきほどの⑬式で与えられるので、⑬式を使うと、抵抗 $R$ にかかる電圧 $e_R(t)$[$ \mathrm{V} $]は次のようになります。
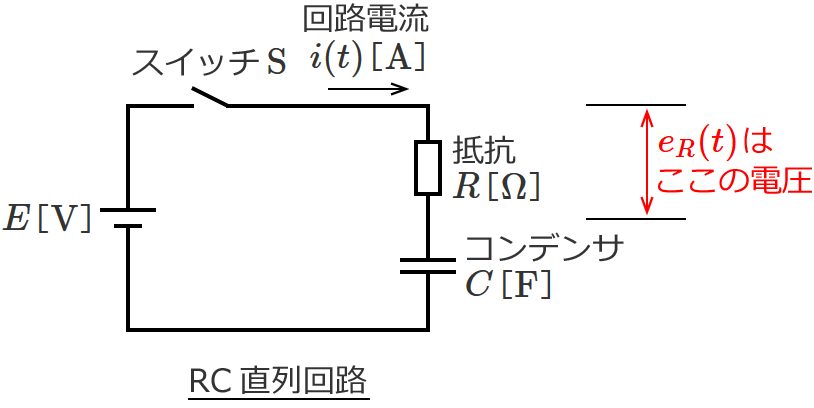
$e_R(t) = i(t) \cdot R$
$= \left( \dfrac{E}{R} \cdot e^{-\frac{1}{CR} t} \right) \cdot R$
$= E \cdot e^{-\frac{1}{CR} t}$
$\therefore e_R(t) = E \cdot e^{-\frac{1}{CR} t}$ …⑭ (これが抵抗 $R$ の電圧)
電流を求めてしまえば、抵抗 $R$ の電圧は簡単に求められますね。
RC直列回路の抵抗Rの電圧のグラフ
グラフについては、電圧 $e_R(t)$ は $i(t)$ に $R$ をかけただけなので、$i(t)$ と同じような形のグラフになります。
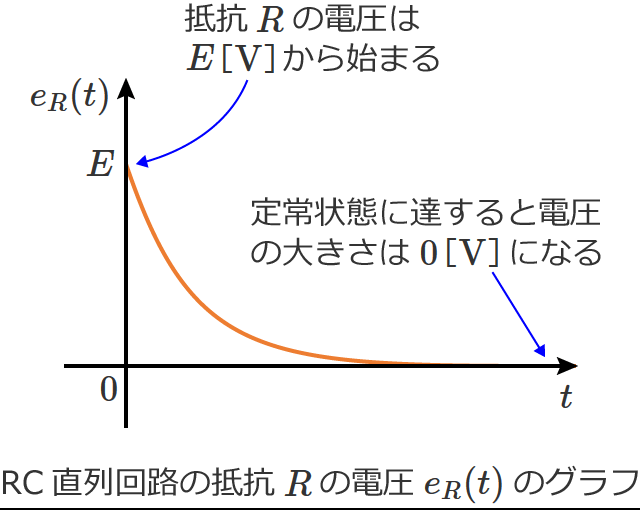
このグラフをみると、抵抗 $R$ の電圧は $E$[$ \mathrm{V} $]から始まり、ある程度時間が経過する(定常状態に達するという意味)と電圧の大きさは $0$[$ \mathrm{V} $]になるのが分かります。
つまり、スイッチをONした直後は電源の電圧がすべて抵抗 $R$ にかかりますが、定常状態に達すると抵抗 $R$ には電圧がかからず、電源の電圧はすべてコンデンサ $C$ にかかることになります。(これ、大事!)
RC直列回路のコンデンサCの電圧の求め方
コンデンサ $C$ の電圧についても求めてみましょう。
ここでもさきほど求めた電流 $i(t)$ の式(⑬式)を使うと、コンデンサ $C$ の電圧 $e_C(t)$[$ \mathrm{V} $]は次のようになります。
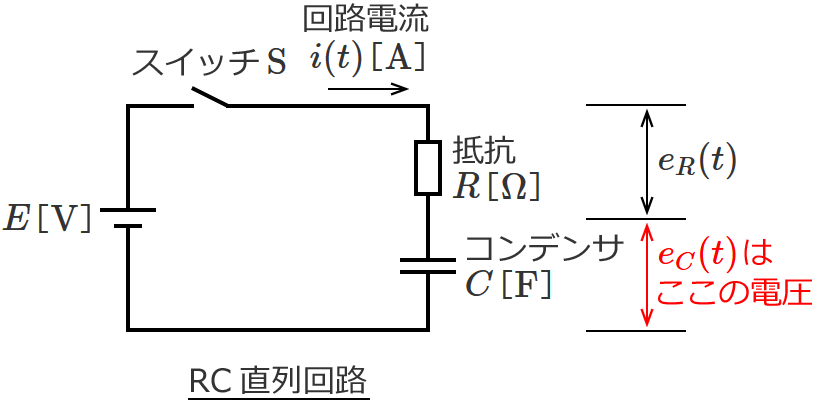
$e_C(t) = \dfrac{1}{C} \displaystyle\int i(t) \, dt$
$= \dfrac{1}{C} \displaystyle\int \left( \dfrac{E}{R} \cdot e^{-\frac{1}{CR} t} \right) \, dt$
この式を解くとコンデンサ $C$ の電圧 $e_C(t)$ を求めることができます。では、解いてみましょう。
$\dfrac{E}{R}$ は定数なので、積分の外に出してしまいます。
$e_C(t) = \dfrac{E}{CR} \displaystyle\int e^{-\frac{1}{CR} t} \, dt$
$= \dfrac{E}{CR} \cdot \dfrac{1}{-\dfrac{1}{CR}} \cdot e^{-\frac{1}{CR} t} + F$
$= -E \cdot e^{-\frac{1}{CR} t} + F$
$\therefore e_C(t) = -E \cdot e^{-\frac{1}{CR} t} + F$ ( $F$ は積分定数) …⑮
⑮式には積分定数があるので、あとは積分定数を求めればいいです。
この回路の場合、時間 $t=0$ のときはコンデンサ $C$ には電荷がなく、つまりコンデンサ $C$ の電圧はゼロなので、初期条件は $t=0$、$e_C(t) = 0$ になります。なので、$t=0$、$e_C(t) = 0$ を⑮式に代入すると、
$0 = -E \cdot e^{-\frac{1}{CR} \times 0} + F$
$0 = -E + F$
$\therefore F = E$ …⑯
積分定数が求められたので、⑯を⑮式に代入します。すると、
$e_C(t) = -E \cdot e^{-\frac{1}{CR} t} + E$
$\therefore e_C(t) = E -E \cdot e^{-\frac{1}{CR} t}$ …⑰ (これがコンデンサ $C$ の電圧)
以上でRC直列回路のコンデンサ $C$ の電圧 $e_C(t)$ が求められました。
コンデンサCの電圧を求める別の計算方法
コンデンサ $C$ の電圧を求めるには、次のように計算してもいいです。
コンデンサ $C$ の電圧は $e_C(t) = \dfrac{1}{C} \displaystyle\int i(t) \, dt$ で与えられますが、電流と電荷の関係式より $i(t) = \dfrac{d \, q(t)}{dt}$ なので、これを代入すると、
$e_C(t) = \dfrac{1}{C} \displaystyle\int \left( \dfrac{d \, q(t)}{dt} \right) \, dt$ $= \dfrac{1}{C} \cdot q(t)$ となるので、この式に既に求めている電荷の式(⑫式)を代入してもいいです。代入してみると、
$e_C(t) = \dfrac{1}{C} \left( CE - CE \cdot e^{-\frac{1}{CR} t} \right)$ $= E - E \cdot e^{-\frac{1}{CR} t}$
$\therefore e_C(t) = E - E \cdot e^{-\frac{1}{CR} t}$ となり、さきほど求めた⑰式と同じになります。
こっちの方が簡単かもね。
RC直列回路のコンデンサCの電圧のグラフ
コンデンサ $C$ の電圧 $e_C(t)$ が求められたのでグラフも書いてみます。
グラフについては、電圧 $e_C(t)$ は電荷 $q(t)$ に $\dfrac{1}{C}$ をかけただけなので、$q(t)$ と同じような形のグラフになります。
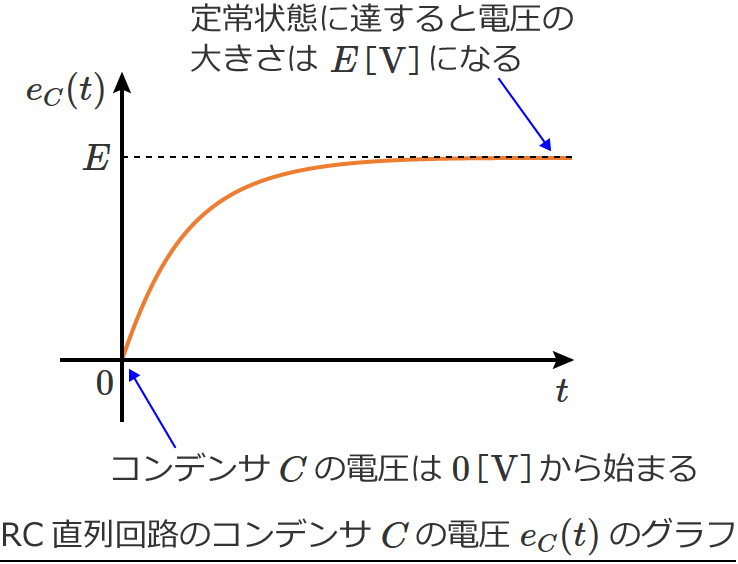
このグラフをみると、コンデンサ $C$ の電圧は $0$[$ \mathrm{V} $]から始まり、ある程度時間が経過する(定常状態に達するという意味)と電圧の大きさは $E$[$ \mathrm{V} $]になるのが分かります。
コンデンサ $C$ の電圧 $e_C(t)$ が最終的に $E$[$ \mathrm{V} $]になるということは、定常状態に達すると電源の電圧がすべてコンデンサ $C$ にかかるということになります。
RC直列回路の過渡現象のまとめ
以上をまとめると次のようになります。
RC直列回路
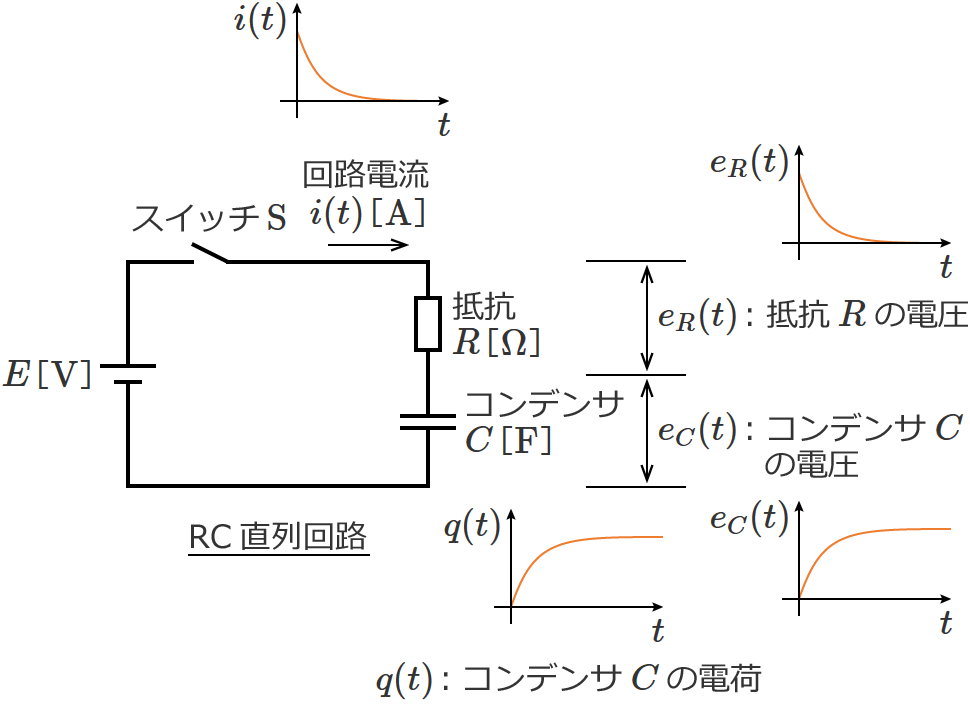
RC直列回路の過渡現象の解き方
❶回路の回路方程式(積分方程式)をたてる
❷電流と電荷の関係式を使って❶の積分方程式を電荷に関する微分方程式にする
❸初期条件から電荷を求める
❹電流と電荷の関係式を使って❸で求めた電荷から電流を求める
❺電圧は❹で求めた電流を使って求める
RC直列回路の過渡現象の式
コンデンサ $C$ の電荷: $q(t) = CE - CE \cdot e^{-\frac{1}{CR} t}$
回路に流れる電流: $i(t) = \dfrac{E}{R} \cdot e^{-\frac{1}{CR} t}$
抵抗 $R$ の電圧: $e_R(t) = E \cdot e^{-\frac{1}{CR} t}$
コンデンサ $C$ の電圧: $e_C(t) = E - E \cdot e^{-\frac{1}{CR} t}$
RC直列回路の時定数
時定数: $\tau = CR$
RC直列回路の過渡現象のグラフ
<電荷のグラフ>
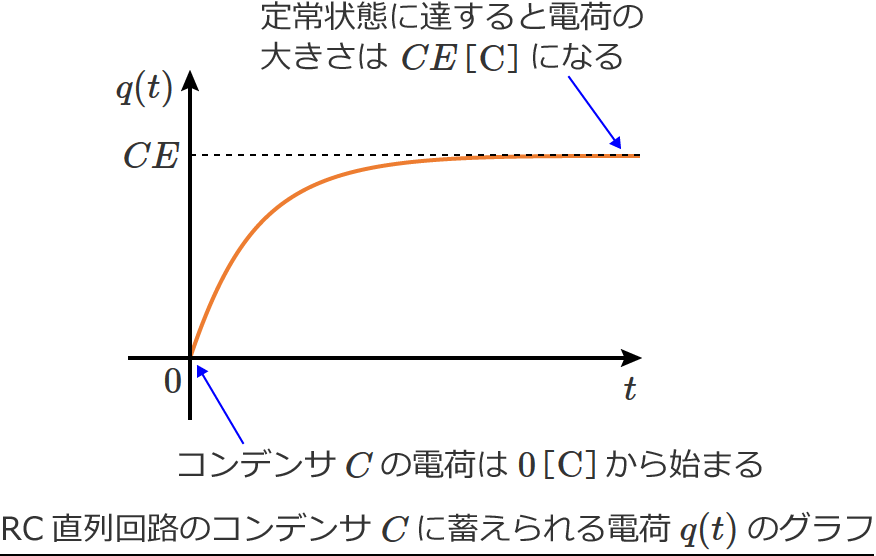
<電流のグラフ>
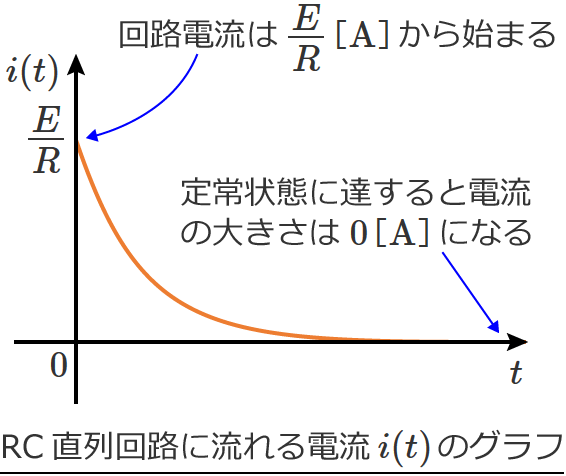
<電圧のグラフ>
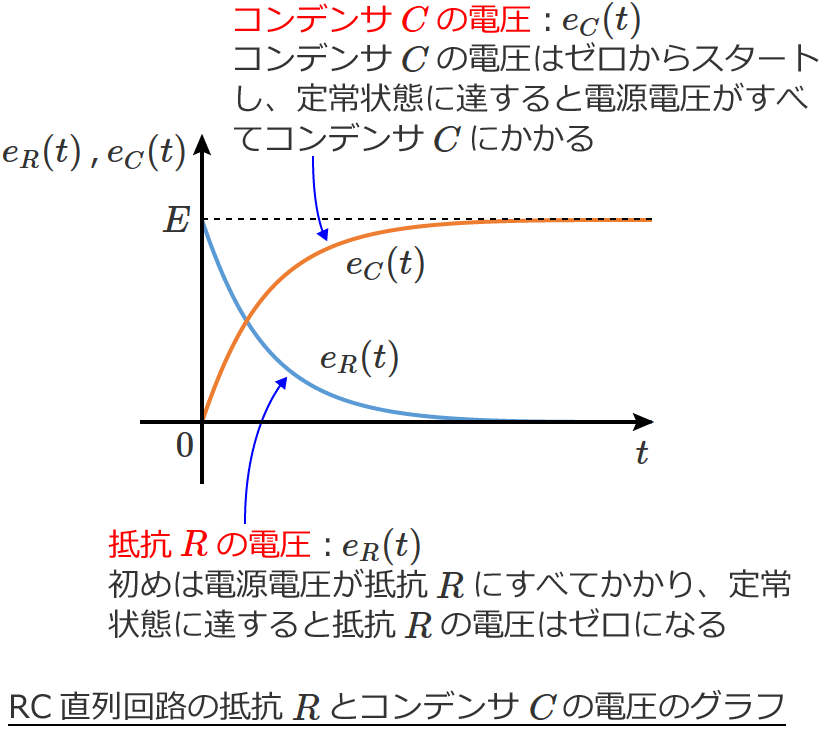
過渡現象を解くためには微分方程式(または積分方程式)を解く必要があるため計算が大変になる場合もありますが、たいていの場合、決まった形の微分方程式を解くだけなので、初めは大変かもしれませんがパターンをおぼえて慣れれば大丈夫ですよ。
それから、電験二種の一次試験の理論では過渡現象の解き方などが出題されることがあり、RL直列回路とRC直列回路の過渡現象の解き方は過渡現象回路を解くための基本になるので、電験二種を受験する方は解き方をおぼえておくようにしましょう。
電験三種を受験する方は過渡現象の解き方までは分からなくてもいいと思いますが、RL直列回路とRC直列回路の過渡現象のグラフと時定数は必ずおぼえておくようにしましょう。
スポンサーリンク
スポンサーリンク
そもそも過渡現象ってなんでしたっけ?という方は、こちらの過渡現象とはのページを参考にしてみてください。
RL直列回路については、こちらのRL直列回路の過渡現象の解き方のページを参考にしてみてください。
ラプラス変換を使ったRC直列回路の過渡現象の解き方については、こちらのラプラス変換によるRC直列回路の過渡現象の解き方のページを参考にしてみてください。
RL直列回路の過渡現象の解き方 ←BACK
NEXT→ ラプラス変換によるRL直列回路の過渡現象の解き方
スポンサーリンク
RC直列回路の過渡現象の解き方 関連ページ
- 過渡現象とは
- 過渡現象について解説しています。過渡現象とは、ある定常状態から別の定常状態に移るまでに起こる現象(電圧や電流などの時間的な変化)のことをいい、過渡現象は回路の状態が変化することによって起こります。
- 時定数
- 過渡現象の時定数について解説しています。時定数は、過渡状態での変化の速さを表わす量で、時定数が小さければ変化する速さは速くなり、時定数が大きければ変化する速さは遅くなります。
- 時定数の単位はなぜ時間s(秒)になるのか?
- 過渡現象の時定数の単位はなぜ時間s(秒)になるのか?について解説しています。時定数の単位が時間(s)になる過程も詳しく書いていますので、参考にしてみてください。
- RL直列回路の時定数(τ=L/R)の導出
- RL直列回路の時定数(τ=L/R)の導出方法について解説しています。RL直列回路の時定数は、電流のt=0における接線と定常状態の電流を表わす直線との交点の時間を算出すると求められます。
- RC直列回路の時定数(τ=CR)の導出
- RC直列回路の時定数(τ=CR)の導出方法について解説しています。RC直列回路の時定数は、電流のt=0における接線と定常状態の電流を表わす直線との交点の時間を算出すると求められます。
- RL直列回路の過渡現象の解き方
- RL直列回路の過渡現象の解き方について解説しています。過渡現象を解くためには微分方程式を解く必要があるため計算がちょっと大変ですが、解き方のパターンをおぼえてしまうとそれほど難しくはありませんよ。
- ラプラス変換によるRL直列回路の過渡現象の解き方
- ラプラス変換によるRL直列回路の過渡現象の解き方について解説しています。ラプラス変換を使ってRL直列回路の過渡現象を解いていますので、ラプラス変換を使った過渡現象の解き方の参考にしてみてください。
- ラプラス変換によるRC直列回路の過渡現象の解き方
- ラプラス変換によるRC直列回路の過渡現象の解き方について解説しています。ラプラス変換を使ってRC直列回路の過渡現象を解いていますので、ラプラス変換を使った過渡現象の解き方の参考にしてみてください。


