スポンサーリンク
ラプラス変換によるRC直列回路の過渡現象の解き方
※ページ内にPR・広告が含まれる場合があります。
次の図のように、抵抗 $R$[$\Omega$]、コンデンサ $C$[$\mathrm{F}$]、直流電源 $E$[$\mathrm{V}$]、スイッチ $\mathrm{S}$ からなるRC直列回路があるとします。(スイッチ $\mathrm{S}$ を入れる前のコンデンサ $C$ に蓄えられている電荷はゼロとします。(つまり、コンデンサの初期電荷はなく、$t=0$ で $q(t)=0$ ))
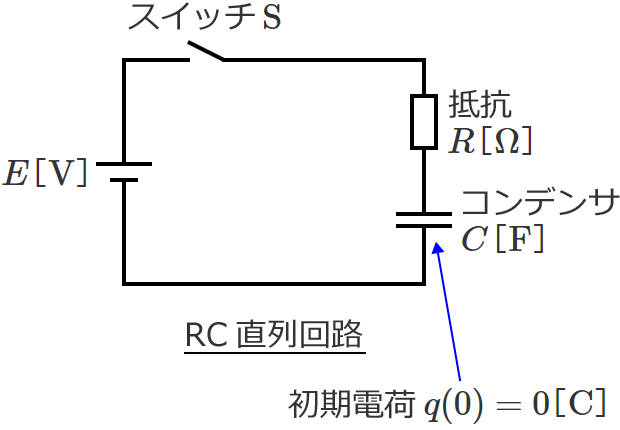
この回路のスイッチをONすると過渡現象が起こるため、スイッチをONすると回路に流れる電流やコンデンサに蓄えられる電荷は時間的に変化し、その後ある程度時間が経過すると一定値に落ち着きます。
このような時間的に変化する過渡現象の電流や電荷の求め方には、回路の回路方程式(微分や積分が含まれる)をたててその方程式をそのまま直接解いていく方法(変数分離法などを使って解いていく方法)の他に、ラプラス変換を使って解いていく方法があります。
このラプラス変換を使ってRC直列回路の過渡現象を解くときの手順は、おおよそ次のような手順になります。
ラプラス変換によるRC直列回路の過渡現象の解き方の手順
❶RC直列回路の回路方程式(微分や積分が含まれる)をたてる
❷❶の方程式をラプラス変換する(初期条件も考慮する)
❸❷でラプラス変換した式を整理する(例:電荷を求めるときは電荷 $Q(s)=$ … の式にする)
❹逆ラプラス変換をするために、❸の式を部分分数分解する
❺❹の式を逆ラプラス変換する
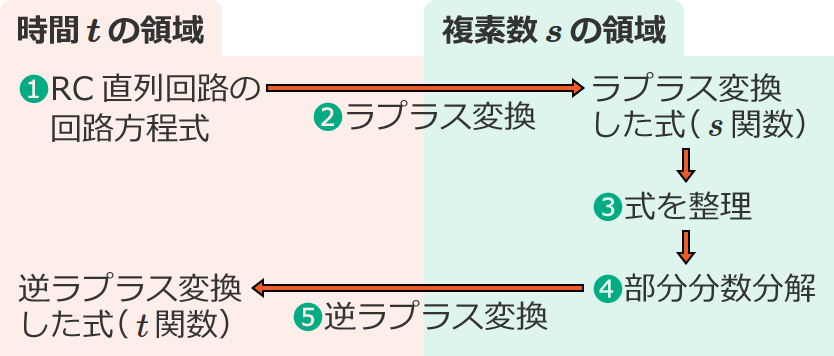
少し複雑に思えるかもしれませんが、ラプラス変換を使って過渡現象を解く場合はだいたいこのような手順になるので、解き方のパターンをおぼえてしまえばそれほど難しく感じなくなります。
また、ラプラス変換を使った計算方法の場合、微分方程式を直接解いていく計算方法よりも計算の手間が少なくなることが多いです。(部分分数分解の計算がちょっとめんどくさい場合もありますが。)
このページでは、RC直列回路の過渡現象をラプラス変換を使って解いていますので、ラプラス変換を使った過渡現象の解き方の参考にしてみてください。
変数分離法を使ったRC直列回路の過渡現象の解き方については、こちらのRC直列回路の過渡現象の解き方のページを参考にしてみてください。
スポンサーリンク
RC直列回路のコンデンサに蓄えられる電荷の求め方
では、ラプラス変換を使って、スイッチ $\mathrm{S}$ をONしたときのRC直列回路に蓄えられる電荷を求めてみます。
まず初めに、回路の回路方程式をたてます。
回路に流れる電流を $i(t)$[$\mathrm{A}$]とすると、抵抗 $R$ での電圧降下は $R\, i(t)$[$\mathrm{V}$]、コンデンサ $C$ での電圧降下は $\dfrac{1}{C}\displaystyle\int i(t)\, dt$[$\mathrm{V}$]なので、
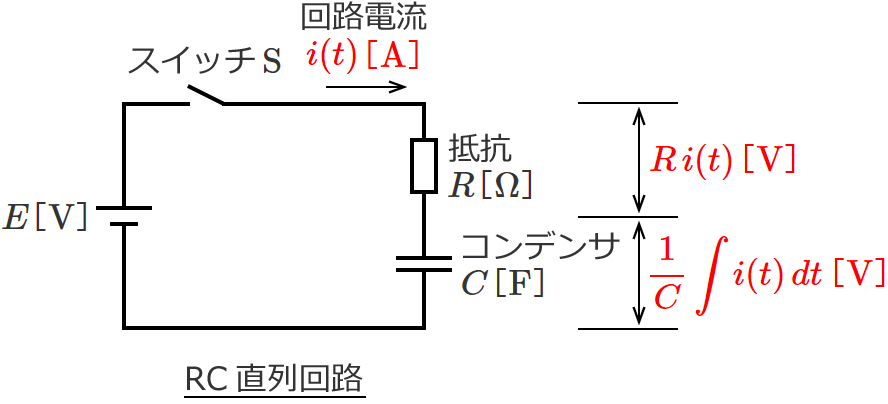
この回路にキルヒホッフの第二法則(電圧則)を適用すれば、回路方程式は次の①式(積分方程式)で与えられます。
$E=R\, i(t)+\dfrac{1}{C}\displaystyle\int i(t)\, dt$ …①
ここで、電流と電荷の関係は $i(t)=\dfrac{d\, q(t)}{dt}$ なので、これを①式に代入して電荷 $q(t)$ の式にします。すると、
$E=R\dfrac{d\, q(t)}{dt} +\dfrac{1}{C} q(t)$ …②
となり、この②式をラプラス変換すると、次の③式になります。
$\dfrac{E}{s} =R\left( s\, Q(s)-q(0)\right) +\dfrac{1}{C} Q(s)$ …③

ラプラス変換するときは、ラプラス変換の公式を利用します。ラプラス変換の公式については、こちらのラプラス変換の公式のページを参考にしてみてください。
③式中の $q(0)$ は初期条件( $t=0$ のときの電荷の値)なので、$q(0)=0$ とすると③式は次の④式になります。
$\dfrac{E}{s} =R\left( s\, Q(s)-0\right) +\dfrac{1}{C} Q(s)$
$\therefore \dfrac{E}{s} =s\, R\, Q(s)+\dfrac{1}{C} Q(s)$ …④
この④式を $Q(s)$ で整理すると、
$\left( s\, R+\dfrac{1}{C}\right) Q(s)=\dfrac{E}{s}$
$Q(s)=\dfrac{E}{s}\dfrac{1}{s\, R+\dfrac{1}{C}}$
$Q(s)=\dfrac{E}{s\left( s\, R+\dfrac{1}{C}\right)}$
右辺の分母と分子を $R$ で割ると、
$Q(s)=\dfrac{\dfrac{E}{R}}{s\left( s+\dfrac{1}{CR}\right)}$
$Q(s)=\dfrac{E}{R}\dfrac{1}{s\left( s+\dfrac{1}{CR}\right)}$ …⑤
となり、この⑤式を逆ラプラス変換すると $t$ 領域(時間 $t$ の領域)の関数 $q(t)$ を求めることができます。なので、⑤式を逆ラプラス変換するために、⑤式の右辺を部分分数分解します。
$\dfrac{E}{R}\dfrac{1}{s\left( s+\dfrac{1}{CR}\right)} =\dfrac{\alpha}{s} +\dfrac{\beta}{s+\dfrac{1}{CR}}$ …⑥ とおくと、
⑥式の右辺 $=\dfrac{\alpha}{s} +\dfrac{\beta}{s+\dfrac{1}{CR}}$
$=\dfrac{\alpha\left( s+\dfrac{1}{CR}\right) +\beta\, s}{s\left( s+\dfrac{1}{CR}\right)}$
$=\dfrac{\alpha\, s+\dfrac{\alpha}{CR} +\beta\, s}{s\left( s+\dfrac{1}{CR}\right)}$
$=\dfrac{(\alpha +\beta )s+\dfrac{\alpha}{CR}}{s\left( s+\dfrac{1}{CR}\right)}$ …⑦
この⑦と⑥式の左辺より、次の2つの式が成り立ちます。
$\left\{\begin{array}{l} \alpha +\beta =0 \quad\text{…⑧} \\ \dfrac{\alpha}{CR} =\dfrac{E}{R} \quad\text{…⑨} \end{array}\right.$
⑨式より、$\dfrac{\alpha}{C} =E$ なので、
$\therefore\alpha =CE$ …⑩
となります。⑩を⑧式に代入すると、$CE+\beta =0$ なので、
$\therefore\beta =-CE$ …⑪
となります。したがって、$Q(s)=\dfrac{E}{R}\dfrac{1}{s\left( s+\dfrac{1}{CR}\right)}$ は次のように部分分数分解できます。
$Q(s)=\dfrac{E}{R}\dfrac{1}{s\left( s+\dfrac{1}{CR}\right)}$
$=\dfrac{\alpha}{s} +\dfrac{\beta}{s+\dfrac{1}{CR}}$
$=\dfrac{CE}{s} +\dfrac{-CE}{s+\dfrac{1}{CR}}$ (⑩と⑪を代入)
$\therefore Q(s)=\dfrac{CE}{s} -\dfrac{CE}{s+\dfrac{1}{CR}}$ …⑫
$Q(s)$ を部分分数分解できたので、あとは⑫式を逆ラプラス変換するだけです。⑫式を逆ラプラス変換すると、
$q(t)=\mathcal{L}^{-1}\left[\, Q(s)\,\right]$
$=\mathcal{L}^{-1}\left[\,\dfrac{CE}{s}\right] +\mathcal{L}^{-1}\left[\, -\dfrac{CE}{s+\dfrac{1}{CR}}\right]$
$=CE\,\mathcal{L}^{-1}\left[\,\dfrac{1}{s}\,\right]$ $-CE\,\mathcal{L}^{-1}\left[\,\dfrac{1}{s+\dfrac{1}{CR}}\right]$
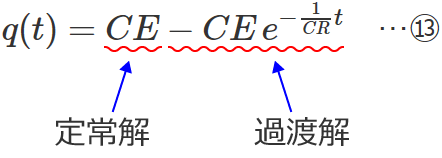
$=CE-CE\, e^{-\frac{1}{CR} t}$
となり、RC直列回路のコンデンサに蓄えられる電荷 $q(t)$ が求められました。
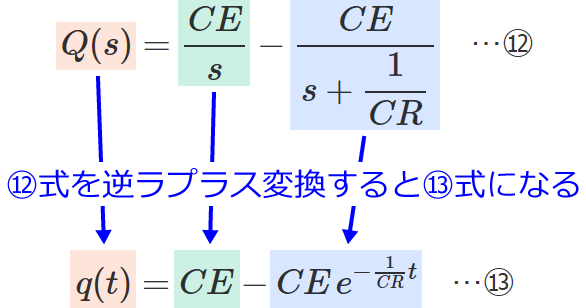
ちなみに、この⑬式の右辺の第1項を定常解、第2項を過渡解といいます。
部分分数分解の別のやり方
$\dfrac{E}{R}\dfrac{1}{s\left( s+\dfrac{1}{CR}\right)} =\dfrac{\alpha}{s} +\dfrac{\beta}{s+\dfrac{1}{CR}}$ …⑥ の部分分数分解で、$\alpha$ と $\beta$ を求める方法には次のような方法もあります。
$\alpha$ を求めるとき
⑥式の両辺に $s$ をかけて、
$\dfrac{E}{R}\dfrac{1}{s+\dfrac{1}{CR}} =\alpha +\dfrac{s\, \beta}{s+\dfrac{1}{CR}}$ (右辺第1項は $\alpha$ だけになる)
$s=0$ を代入すると、
$\dfrac{E}{R}\dfrac{1}{0+\dfrac{1}{CR}} =\alpha$ ($\beta$ が消える)
$\alpha =\dfrac{E}{R}\times CR=CE$
$\therefore\alpha =CE$ (これが $\alpha$ )
$\beta$ を求めるとき
⑥式の両辺に $s+\dfrac{1}{CR}$ をかけて、
$\dfrac{E}{R}\dfrac{1}{s} =\dfrac{\alpha}{s}\left( s+\dfrac{1}{CR}\right) +\beta$ (右辺第2項は $\beta$ だけになる)
$s=-\dfrac{1}{CR}$ を代入すると、
$\dfrac{E}{R}\dfrac{1}{-\dfrac{1}{CR}} =\beta$ ($\alpha$ が消える)
$\beta =\dfrac{E}{R}\times (-CR)=-CE$
$\therefore\beta =-CE$ (これが $\beta$ )
となり、ここで求めた $\alpha$ と $\beta$ は、さきほど求めた $\alpha$ と $\beta$ に一致します。
スポンサーリンク
スポンサーリンク
RC直列回路のコンデンサに蓄えられる電荷のグラフ
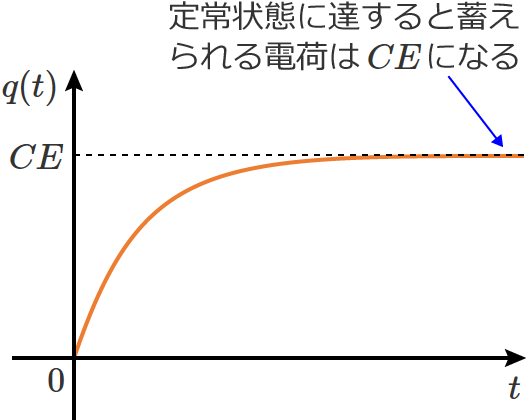
電荷 $q(t)$ のグラフを書いてみると、次のようなグラフになり、
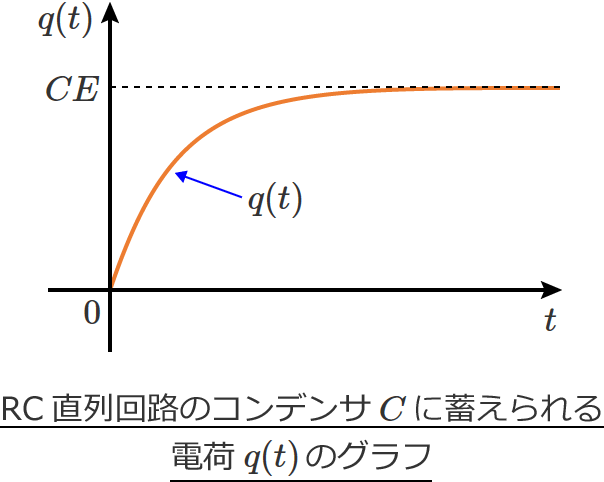
RC直列回路のコンデンサに蓄えられる電荷 $q(t)$ は時間がたつにつれて増加がゆるやかになり、ある程度時間が経過して定常状態に達すると、$q(t)=CE$ の一定値になります。
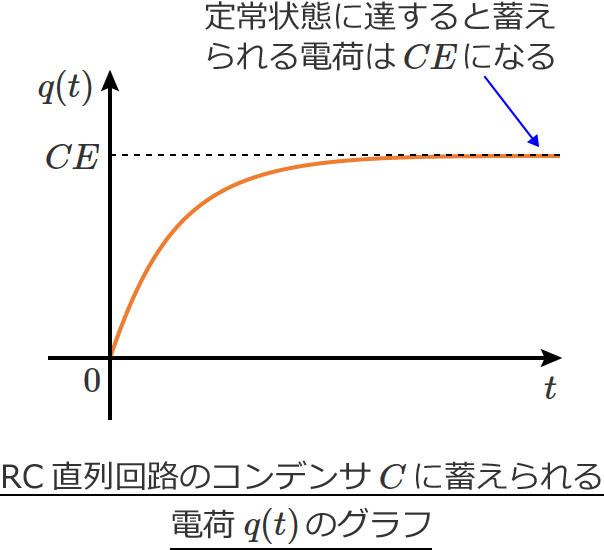
なお、RC直列回路の時定数 $\tau$ は、$\tau =CR$ になります。
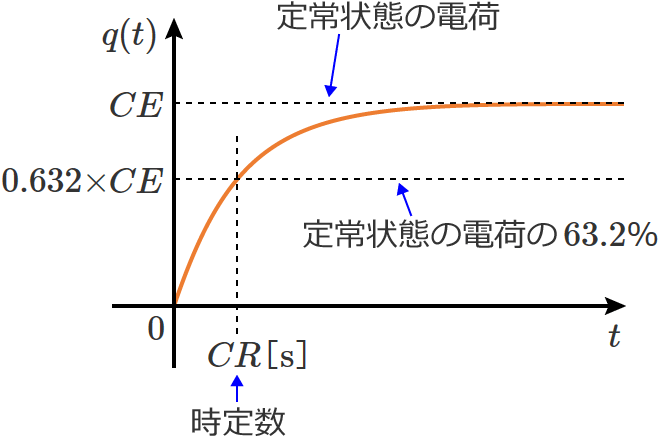
時定数は、過渡状態での変化の速さを表わす値です。時定数については、こちらの時定数のページを参考にしてみてください。
ちなみに、RC直列回路に流れる電流 $i(t)$ の式は、電荷 $q(t)$ の式(⑬式)を使って次のように求めることができます、よ!
電流と電荷の関係は $i(t)=\dfrac{d\, q(t)}{dt}$ なので、これに電荷 $q(t)$ を代入すると、
$i(t)=\dfrac{d\, q(t)}{dt}$
$=\dfrac{d}{dt}\left( CE-CE\, e^{-\frac{1}{CR} t}\right)$
$=-CE\,\dfrac{d}{dt} e^{-\frac{1}{CR} t}$
$=-CE\times\left( -\dfrac{1}{CR}\right) e^{-\frac{1}{CR} t}$
$=\dfrac{E}{R} e^{-\frac{1}{CR} t}$
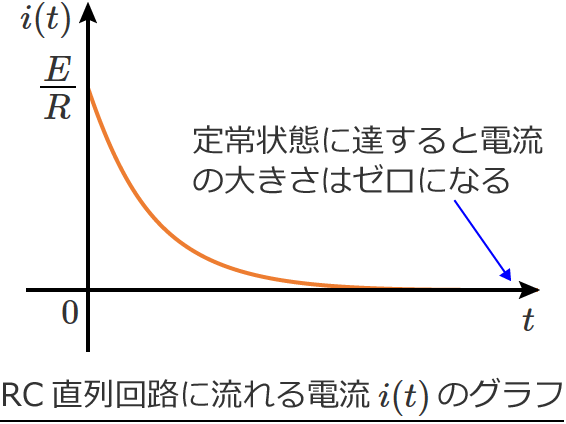
$\therefore i(t)=\dfrac{E}{R} e^{-\frac{1}{CR} t}$ (これがRC直列回路に流れる電流)
となり、RC直列回路に流れる電流 $i(t)$ が求められました。$i(t)$ は $q(t)$ を求めてしまえば、$q(t)$ を微分するだけなので簡単に求められます。
以上をまとめると、次のようになります。
ラプラス変換によるRC直列回路の過渡現象の解き方
❶RC直列回路の回路方程式(微分や積分が含まれる)をたてる
❷❶の方程式をラプラス変換する(初期条件も考慮する)
❸❷でラプラス変換した式を整理する(例:電荷を求めるときは電荷 $Q(s)=$ … の式にする)
❹逆ラプラス変換をするために、❸の式を部分分数分解する
❺❹の式を逆ラプラス変換する
RC直列回路のコンデンサに蓄えられる電荷の過渡現象の式
$q(t)=CE-CE\, e^{-\frac{1}{CR} t}$
RC直列回路のコンデンサに蓄えられる電荷の過渡現象のグラフ
RC直列回路の時定数
$\tau =CR$
スポンサーリンク
スポンサーリンク
微分方程式を直接解く過渡現象の解き方については、こちらのRC直列回路の過渡現象の解き方のページを参考にしてみてください。こちらのページでは、抵抗 $R$ の電圧、コンデンサ $C$ の電圧なども求めています。
ラプラス変換を使ったRL直列回路の過渡現象の解き方については、こちらのラプラス変換によるRL直列回路の過渡現象の解き方のページを参考にしてみてください。
そもそも過渡現象ってなんでしたっけ?という方は、こちらの過渡現象とはのページを参考にしてみてください。
ラプラス変換によるRL直列回路の過渡現象の解き方 ←BACK
NEXT→ 電気のお勉強のTOP
スポンサーリンク
ラプラス変換によるRC直列回路の過渡現象の解き方 関連ページ
- 過渡現象とは
- 過渡現象について解説しています。過渡現象とは、ある定常状態から別の定常状態に移るまでに起こる現象(電圧や電流などの時間的な変化)のことをいい、過渡現象は回路の状態が変化することによって起こります。
- 時定数
- 過渡現象の時定数について解説しています。時定数は、過渡状態での変化の速さを表わす量で、時定数が小さければ変化する速さは速くなり、時定数が大きければ変化する速さは遅くなります。
- 時定数の単位はなぜ時間s(秒)になるのか?
- 過渡現象の時定数の単位はなぜ時間s(秒)になるのか?について解説しています。時定数の単位が時間(s)になる過程も詳しく書いていますので、参考にしてみてください。
- RL直列回路の時定数(τ=L/R)の導出
- RL直列回路の時定数(τ=L/R)の導出方法について解説しています。RL直列回路の時定数は、電流のt=0における接線と定常状態の電流を表わす直線との交点の時間を算出すると求められます。
- RC直列回路の時定数(τ=CR)の導出
- RC直列回路の時定数(τ=CR)の導出方法について解説しています。RC直列回路の時定数は、電流のt=0における接線と定常状態の電流を表わす直線との交点の時間を算出すると求められます。
- RL直列回路の過渡現象の解き方
- RL直列回路の過渡現象の解き方について解説しています。過渡現象を解くためには微分方程式を解く必要があるため計算がちょっと大変ですが、解き方のパターンをおぼえてしまうとそれほど難しくはありませんよ。
- RC直列回路の過渡現象の解き方
- RC直列回路の過渡現象の解き方について解説しています。RC直列回路の過渡現象はRL直列回路よりもちょっとだけ計算が大変ですが、解き方のパターンは同じなので、おぼえてしまうとそれほど難しくはありませんよ。
- ラプラス変換によるRL直列回路の過渡現象の解き方
- ラプラス変換によるRL直列回路の過渡現象の解き方について解説しています。ラプラス変換を使ってRL直列回路の過渡現象を解いていますので、ラプラス変換を使った過渡現象の解き方の参考にしてみてください。


