�X�|���T�[�����N
�d���O��u���_�v����21�N�x ��5�̉ߋ���Ɖ��
���y�[�W����PR��L�����܂܂��ꍇ������܂��B
�d���O��u���_�v����21�N�x��5�̉ߋ���̉���ł��B
�d���O��u���_�v����21�N�x�i2009�N�x�j�@��5
�d���O��u���_�v�̕���21�N�x��5�iA���j�̖��ł��B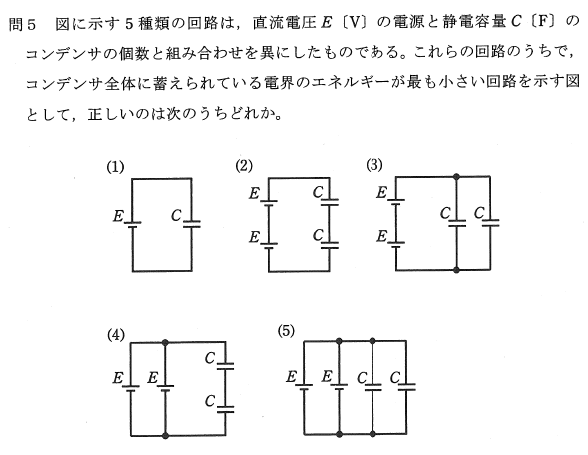
���̖����������߂̃|�C���g
���̖����������߂̃|�C���g�́A
- �����d��������܂��͕���ɐڑ����ꂽ�Ƃ��A���̓d���̓d���͂ǂ��Ȃ�́H
- �R���f���T������܂��͕���ɐڑ����ꂽ�Ƃ��̍����Ód�e�ʂ̌����͕�����܂����H
- �R���f���T�ɒ~������d�E�̃G�l���M�[�i�Ód�G�l���M�[�j�̌����͕�����܂����H
�ł��B
�X�|���T�[�����N
�X�|���T�[�����N
�d���O��u���_�v����21�N�x�i2009�N�x�j�@��5�iA���j�̉��
���̉ߋ���̓R���f���T�ɒ~���炦��d�E�̃G�l���M�[�i�Ód�G�l���M�[�j�Ɋւ�����ŁA�i1�j�`�i5�j�̉�H�̒��ŃR���f���T�S�̂ɒ~������d�E�̃G�l���M�[���ł��������̂͂ǂꂩ�H�@�Ƃ������ł��B
��蕶�����Ă݂�ƁA�u�R���f���T�S�̂ɒ~�����Ă���d�E�̃G�l���M�[���ł���������H�v�Ə����Ă��܂���ˁH
�R���f���T�S���Ə����Ă���̂ŁA�i2�j�`�i5�j�̃R���f���T�͂��ꂼ�ꍇ�����Ă��܂��āA���̍��������R���f���T�ɒ~������d�E�̃G�l���M�[�����߂āA�Ō�ɑ傫�����r��������ł��B
����ŁA���̖��ł͊e��H�̓d�E�̃G�l���M�[�����߂Ȃ���Ȃ�܂��A�d�E�̃G�l���M�[�����߂�����͕�����܂����H�@���ꂪ������Ȃ��ƁA�ǂ��ɂ������܂���B
�R���f���T�̐Ód�e�ʂ� $C$�m$\mathrm{F}$�n�A�R���f���T�ɂ�����d���� $E$�m$\mathrm{V}$�n�Ƃ���ƁA�d�E�̃G�l���M�[ $W$�m$\mathrm{J}$�n�́A
$W=\dfrac{1}{2} CE^2$�@�m$\mathrm{J}$�n�@�ł��ˁB
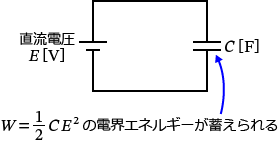
�ł́A�i1�j�`�i5�j�̉�H���ꂼ��̓d�E�̃G�l���M�[�����߂Ă݂܂��傤�B
�i1�j�̉�H�̃R���f���T�ɒ~������d�E�̃G�l���M�[
�i1�j�́A���̂悤�ȉ�H�}�ł��B
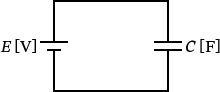
������āA�������̂܂�܂ł����܂��ˁI
�i1�j�̉�H�̃R���f���T�S�́i�ƌ����Ă�1�����Ȃ��j�ɒ~������d�E�̃G�l���M�[ $W_1$ �́A
$\therefore W_1=\dfrac{1}{2} CE^2$�@�m$\mathrm{J}$�n�@�c�@�@�ƂȂ�܂��B
����͉����l���Ȃ��Ă����̂ŁA����ȒP�ł��ˁB
�i2�j�̉�H�̃R���f���T�ɒ~������d�E�̃G�l���M�[
�i2�j�́A���̂悤�ȉ�H�}�ł��B
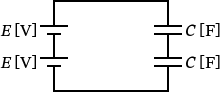
�i1�j�̉�H�}�Ƃ͈���āA�d����2�A�R���f���T��2�ɂȂ��Ă��܂��B
���̂悤�ȏꍇ�ɂ́A�ЂƂ܂��A�d�����ƃR���f���T���ŕ����čl���Ă݂܂��傤�B�܂��͓d��������B
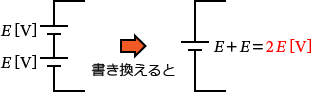
�d�����ɂ́A�d�� $E$�m$\mathrm{V}$�n�̓d����2����ɐڑ�����Ă��܂��B�Ȃ̂ŁA�d�����́A
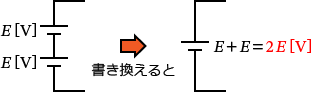
�Ə��������邱�Ƃ��ł��܂��ˁB����͗Ⴆ�A$1.5\,\mathrm{V}$ �̊��d�r2��ɐڑ�����Ɠd���� $1.5\times 2=3\,\mathrm{V}$ �ɂȂ�܂���ˁH�@����Ɠ������Ƃł��B
���́A�R���f���T���ł��B
�R���f���T���ɂ́A�Ód�e�� $C$�m$\mathrm{F}$�n�̃R���f���T��2����ɐڑ�����Ă��܂��B�Ȃ̂ŁA�R���f���T��2����ڑ��̂Ƃ��̍����Ód�e�ʂ̌������g���āA�R���f���T��1�ɍ������Ă��܂��܂��B����ƁA
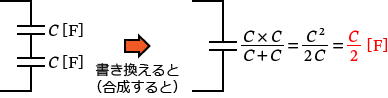
�Ə���������i��������j���Ƃ��ł��܂��ˁB�i�R���f���T��2����ڑ��̂Ƃ��ɂ́A�a���̐ςŋ��߂��܂��B�j
����ƈȏ���A�i2�j�̉�H�}�͎��̂悤�ɏ��������邱�Ƃ��ł��܂��B
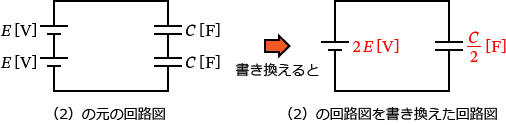
���Ƃ͉E�̉�H�}��d�E�̃G�l���M�[�̌����ɂ��Ă͂߂邾���Ȃ̂ŁA�i2�j�̉�H�̃R���f���T�S�̂ɒ~������d�E�̃G�l���M�[ $W_2$ �́A
$W_2=\dfrac{1}{2}\cdot\left(\dfrac{C}{2}\right)\cdot\left( 2E\right)^2$ $=\dfrac{1}{2}\times\dfrac{C}{2}\times 4E^2$ $=CE^2$
$\therefore W_2=CE^2$�@�m$\mathrm{J}$�n�@�c�A�@�ƂȂ�܂��B
�i3�j�̉�H�̃R���f���T�ɒ~������d�E�̃G�l���M�[
�i3�j�́A���̂悤�ȉ�H�}�ł��B
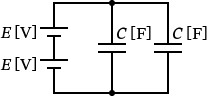
�i3�j�̉�H�́A�d����2����ڑ��A�R���f���T��2����ڑ��ɂȂ��Ă��܂��B������i2�j�̉�H�Ɠ����悤�ɓd�����ƃR���f���T���ŕ����čl���܂��傤�B
�d�����ɂ��Ắi2�j�̉�H�}�Ɠ����Ȃ̂ŁA����������Ǝ��̂悤�ɂȂ�܂��ˁB
�R���f���T���́A�Ód�e�� $C$�m$\mathrm{F}$�n�̃R���f���T��2����ɐڑ�����Ă��܂��B�Ȃ̂ŁA�R���f���T��2����ڑ��̂Ƃ��̍����Ód�e�ʂ̌������g���āA�R���f���T��1�ɍ������Ă��܂��܂��B����ƁA

�Ə���������i��������j���Ƃ��ł��܂��ˁB�i�R���f���T��2����ڑ��̂Ƃ��ɂ́A�������������ŋ��߂��܂��B�j
����ƈȏ���A�i3�j�̉�H�}�͎��̂悤�ɏ��������邱�Ƃ��ł��܂��B
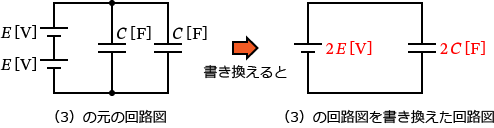
���Ƃ͉E�̉�H�}��d�E�̃G�l���M�[�̌����ɂ��Ă͂߂邾���Ȃ̂ŁA�i3�j�̉�H�̃R���f���T�S�̂ɒ~������d�E�̃G�l���M�[ $W_3$ �́A
$W_3=\dfrac{1}{2}\cdot\left( 2C\right)\cdot\left( 2E\right)^2$ $=\dfrac{1}{2}\times 2C\times 4E^2$ $=C\times 4E^2$ $=4CE^2$
$\therefore W_3=4CE^2$�@�m$\mathrm{J}$�n�@�c�B�@�ƂȂ�܂��B
�i4�j�̉�H�̃R���f���T�ɒ~������d�E�̃G�l���M�[
�i4�j�́A���̂悤�ȉ�H�}�ł��B
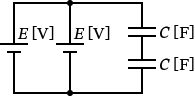
�i4�j�̉�H�́A�d����2����ڑ��A�R���f���T��2����ڑ��ɂȂ��Ă��܂��B����������悤�ɓd�����ƃR���f���T���ŕ����čl���܂��傤�B
�d�����́A�d�� $E$�m$\mathrm{V}$�n�̓d����2����ɐڑ�����Ă��܂��B�Ȃ̂œd�����́A

�Ə��������邱�Ƃ��ł��܂��B����͗Ⴆ�A$1.5\,\mathrm{V}$ �̊��d�r2�����ɐڑ�����Ɠd���͕ς�炸�ɂ��̂܂� $1.5\,\mathrm{V}$ �ɂȂ�܂���ˁH�@����Ɠ������Ƃł��B
�R���f���T���́A�Ód�e�� $C$�m$\mathrm{F}$�n�̃R���f���T��2����ɐڑ�����Ă��܂��B�Ȃ̂ŁA�i2�j�Ɠ����悤�ɃR���f���T��2����ڑ��̂Ƃ��̍����Ód�e�ʂ̌������g���āA�R���f���T��1�ɍ������Ă��܂��܂��B����ƁA
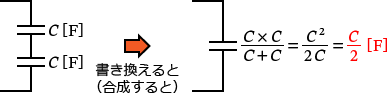
�Ə���������i��������j���Ƃ��ł��܂��ˁB
����ƈȏ���A�i4�j�̉�H�}�͎��̂悤�ɏ��������邱�Ƃ��ł��܂��B
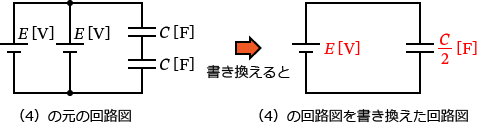
���Ƃ͉E�̉�H�}��d�E�̃G�l���M�[�̌����ɂ��Ă͂߂邾���Ȃ̂ŁA�i4�j�̉�H�̃R���f���T�S�̂ɒ~������d�E�̃G�l���M�[ $W_4$ �́A
$W_4=\dfrac{1}{2}\cdot\left(\dfrac{C}{2}\right)\cdot E^2=\dfrac{C}{4}\times E^2$ $=\dfrac{CE^2}{4}$
$\therefore W_4=\dfrac{1}{4} CE^2$�@�m$\mathrm{J}$�n�@�c�C�@�ƂȂ�܂��B
�i5�j�̉�H�̃R���f���T�ɒ~������d�E�̃G�l���M�[
�i5�j�́A���̂悤�ȉ�H�}�ł��B
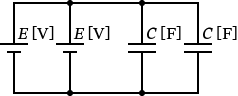
�i5�j�̉�H�́A�d����2����ڑ��A�R���f���T��2����ڑ��ɂȂ��Ă��܂��B
�d�����́A�d�� $E$�m$\mathrm{V}$�n�̓d����2����ɐڑ�����Ă���̂ŁA

�Ə��������邱�Ƃ��ł��܂��B�i4�j�Ɠ����ł��ˁB
�R���f���T���́A�Ód�e�� $C$�m$\mathrm{V}$�n�̃R���f���T��2����ɐڑ�����Ă��܂��B�Ȃ̂ŁA�i3�j�Ɠ����悤�ɃR���f���T��2����ڑ��̂Ƃ��̍����Ód�e�ʂ̌������g���āA�R���f���T��1�ɍ������Ă��܂��܂��B����ƁA

�Ə���������i��������j���Ƃ��ł��܂��ˁB
����ƈȏ���A�i5�j�̉�H�}�͎��̂悤�ɏ��������邱�Ƃ��ł��܂��B
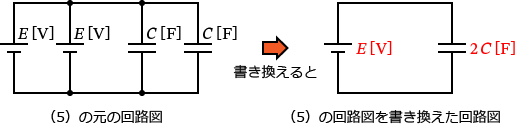
���Ƃ͉E�̉�H�}��d�E�̃G�l���M�[�̌����ɂ��Ă͂߂邾���Ȃ̂ŁA�i5�j�̉�H�̃R���f���T�S�̂ɒ~������d�E�̃G�l���M�[ $W_5$ �́A
$W_5=\dfrac{1}{2}\cdot\left( 2C\right)\cdot E^2=\dfrac{1}{2}\times 2C\times E^2$ $=C\times E^2$ $=CE^2$
$\therefore W_5=CE^2$�@�m$\mathrm{J}$�n�@�c�D�@�ƂȂ�܂��B
�ȏ�Łi1�j�`�i5�j�̉�H�̃R���f���T�S�̂ɒ~������d�E�̃G�l���M�[ $W_1$�A$W_2$�A$W_3$�A$W_4$�A$W_5$ �����߂��܂����B
����Ŗ��́A�d�E�̃G�l���M�[���ł���������H�͂ǂꂩ�H�Ȃ̂ŁA�@�`�D�̒��ň�ԏ��������̂����ɂȂ�܂��B�@�`�D����ׂĂ݂�ƁA
$W_1=\dfrac{1}{2} CE^2$�@�m$\mathrm{J}$�n�@�c�@
$W_2=CE^2$�@�m$\mathrm{J}$�n�@�c�A
$W_3=4CE^2$�@�m$\mathrm{J}$�n�@�c�B
$W_4=\dfrac{1}{4} CE^2$�@�m$\mathrm{J}$�n�@�c�C
$W_5=CE^2$�@�m$\mathrm{J}$�n�@�c�D
�ƂȂ�A���̒��ň�ԏ������̂� $W_4$ �Ȃ̂ŁA���́i4�j�ɂȂ�܂��B�@�E�E�E�i���j
���̖����������߂Ɏg��������
�R���f���T�ɒ~������d�E�̃G�l���M�[�i�Ód�G�l���M�[�j�̌����F$W=\dfrac{1}{2} CV^2$
�R���f���T2������ڑ��̂Ƃ��̍����Ód�e�ʂ̌����F$C=\dfrac{C_1C_2}{C_1+C_2}$
�R���f���T2������ڑ��̂Ƃ��̍����Ód�e�ʂ̌����F$C=C_1+C_2$
�d�E�̃G�l���M�[�ƐÓd�G�l���M�[�͈Ⴄ�́H
���̖�蕶�ł̓R���f���T�ɒ~������G�l���M�[���u�d�E�̃G�l���M�[�v�Ə����Ă��܂����A���̃G�l���M�[�́u�Ód�G�l���M�[�v�ƌ����Ƃ�������܂��B�܂�A�u�d�E�̃G�l���M�[�v�Ɓu�Ód�G�l���M�[�v�͓����Ӗ��ƍl���Ă����ł��B
���̖��̂悤�ɓd���O��̖��ł́A�I�����́i1�j�`�i5�j�܂ł��ׂČv�Z���ē��������悭�o�肳��܂��B�i1�j�`�i5�j�܂ł��ׂČv�Z����̂͑�ςł����A�u�߂�ǂ����`�I�v�Ǝv�킸�Ɉ��m���Ɍv�Z���Ă����悤�ɂ��܂��傤�B
�v�Z���Ă݂�ƁA���̃��x���Ƃ��Ă͂���Ȃɓ���Ȃ��A�ӊO�ɊȒP�Ɍv�Z�ł��Ă��܂���肾�����肷�邱�Ƃ������ł���B
�X�|���T�[�����N
�X�|���T�[�����N
�R���f���T�̍����Ód�e�ʂɂ��Ă悭������Ȃ����������Ód�e�ʂ̋��ߕ��i�v�Z���@�j�̃y�[�W���Q�l�ɂ��Ă݂Ă��������B�R���f���T�ɒ~������d�ׂɂ��Ă��R���f���T�̐Ód�e�ʂƓd�ׂ̌v�Z�̊�{�i����ڑ��ƕ���ڑ��j�̃y�[�W���Q�l�ɂȂ�Ǝv���܂��B
�������߂��d���O��̉ߋ����W�͂������A�d���O��̎Q�l���͂������A�d���O��p�̐��w�Q�l���͂������ŏЉ�Ă��܂��̂ŎQ�l�ɂ��Ă݂Ă��������B
�X�|���T�[�����N
�d���O��u���_�v����21�N�x ��5�̉ߋ���Ɖ���@�֘A�y�[�W
- �d���O��u���_�v����21�N�x ��1�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��1�̉ߋ���Ɖ���ł��B���̉ߋ���͓d���A�d�E�A�R���f���T�Ɋւ����{�I�Ȍ�����������Ή�������ł��B
- �d���O��u���_�v����21�N�x ��2�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��2�̉ߋ���Ɖ���ł��B���̉ߋ���͐Ód�E�Ɋւ����{�I�Ȓm���̐����₤���ł��B
- �d���O��u���_�v����21�N�x ��3�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��3�̉ߋ���Ɖ���ł��B���̉ߋ���̓R�C���̎������𐔂ƃR�C���ɒ~�����鎥�C�G�l���M�[�Ɋւ�����ł��B
- �d���O��u���_�v����21�N�x ��4�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��4�̉ߋ���Ɖ���ł��B���̉ߋ���͐�`�����ɗ����d���ɂ�����鎥�E�Ɋւ�����ł��B�d���O��ł悭�o�肳��₷���p�^�[���̖��ł��B
- �d���O��u���_�v����21�N�x ��6�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��6�̉ߋ���Ɖ���ł��B���̉ߋ���͒�R������ڑ��A����ڑ����ꂽ������H�̊�{�I�Ȗ��ŁA�^����ꂽ�d���E�d���̉�H���������R�l�����߂���ł��B�����ł̓L���q�z�b�t�̖@�����g���ĉ����Ă��܂��B
- �d���O��u���_�v����21�N�x ��7�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��7�̉ߋ���Ɖ���ł��B���̉ߋ���͒P��3�����𗬉�H�̌v�Z���ŁA3���ɗ����e���d���̑傫���̑召�W�����߂���ł��B�d�����Ɋe���ׂɗ����d�������߁A�L���q�z�b�t�̖@���i�d�����j��K�p���Ċe���d�������߂܂��B
- �d���O��u���_�v����21�N�x ��8�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��8�̉ߋ���Ɖ���ł��B���̉ߋ���͒P���𗬉�H�̌v�Z���ŁA�X�C�b�`S���J���Ă���Ƃ��ƕ��Ă���Ƃ��̂��ꂼ��̓d���̔�ƈʑ����̍������߂���ł��B�X�C�b�`S���J���Ă���Ƃ��ƕ��Ă���Ƃ��ŕ����Čv�Z���Ă����܂��B
- �d���O��u���_�v����21�N�x ��9�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��9�̉ߋ���Ɖ���ł��B���̉ߋ���͐����g�𗬓d���Ɋւ�����ŁA�d���̏u���l������l�ɂȂ�Ƃ��̎��������߂���ł��B�d�C�̖��ƌ��������A�قڐ��w�̖��ɋ߂��ł��B


