�X�|���T�[�����N
�d���O��u���_�v����21�N�x ��2�̉ߋ���Ɖ��
���y�[�W����PR��L�����܂܂��ꍇ������܂��B
�d���O��u���_�v����21�N�x��2�̉ߋ���̉���ł��B
�d���O��u���_�v����21�N�x�i2009�N�x�j�@��2
�d���O��u���_�v�̕���21�N�x��2�iA���j�̖��ł��B
���̖����������߂̃|�C���g
���̖����������߂̃|�C���g�́A
- �N�[�����̖@���ȂǓ_�d�ׂɊւ����{�I�Ȍ�����m���Ă��邩�H
- �d�C�͐���d�E�i�d��j�Ȃǂ̐Ód�E�Ɋւ����{�I�Ȃ��Ƃ�m���Ă��邩�H
�ł��B
�X�|���T�[�����N
�X�|���T�[�����N
�d���O��u���_�v����21�N�x�i2009�N�x�j�@��2�iA���j�̉��
�i1�j�N�[�����̖@���Ɋւ�����
��蕶�̋L�q�i1�j
��̏����ȑѓd�̂̊Ԃɓ����͂̑傫���́A���ꂼ��̑ѓd�̂̓d�C�ʂ̘a�ɔ�Ⴕ�A���̋�����2��ɔ���Ⴗ��B
�i1�j�́u��̏����ȑѓd�̂̊Ԃɓ����͂̑傫���́A�E�E�E�v�Ƃ������͂Ŏn�܂��Ă��āA����ɑ������͂ɂ́u�����ɔ��v�Ƃ��u�����ɔ����v�Ə����Ă���̂ŁA�N�[�����̖@���̌����ɂ��ď����Ă��镶�͂ł��邱�Ƃ�������܂��B
�Ȃ̂ŁA�����Ă��镶�͂��N�[�����̖@���̌����ƍ����Ă��邩�H����Ă��邩�H������������ł��B
�����Ă��镶�͂����̂܂��ŏ����Ă݂܂��傤�B
��̏����ȑѓd�̂̊Ԃɓ����͂̑傫���� $F$�A���ꂼ��̑ѓd�̂̓d�C�ʂ� $q_1$�A$q_2$�A��̑ѓd�̂̋����� $r$�A���萔�� $k$ �Ƃ���ƁA��蕶�ɏ�����Ă���Ӗ��̎��͎��̂悤�ɂȂ�܂��B
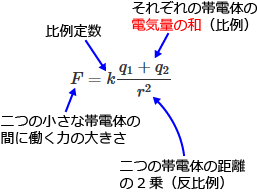
���̎��̓N�[�����̖@���̌����ɂȂ��Ă���ł��傤���H
�N�[�����̖@���̌����́A
$F=k\dfrac{q_1\times q_2}{r^2}$�@�ł���ˁH
��蕶�̈Ӗ��̎��ƃN�[�����̖@���̌���������ׂ�ƁA�E�ӂ̕��q������Ă��āA��蕶�̈Ӗ��̎��̕�����̓d�C�ʂ̘a�i�����Z�j�A�N�[�����̖@���̌����̕�����̓d�C�ʂ̐ρi�|���Z�j�ɂȂ��Ă��܂��B
�Ȃ̂ŁA���́i1�j�̕��͂͊Ԉ���Ă��邱�ƂɂȂ�܂��B
�i2�j�_�d�ׂ����d�E�Ɋւ�����
��蕶�̋L�q�i2�j
�_�d�ׂ����d�E�͓_�d�ׂ̓d�C�ʂɔ�Ⴕ�A�����ɔ���Ⴗ��B
�i2�j�́u�_�d�ׂ����d�E�́E�E�E�v�Ƃ������͂Ŏn�܂��Ă��āA����ɑ������͂ɂ́u�����ɔ��v�Ƃ��u�����ɔ����v�Ə����Ă���̂ŁA�_�d�ׂ����d�E�̌����ɂ��ď����Ă��镶�͂ł��邱�Ƃ�������܂��B
�Ȃ̂ŁA�����Ă��镶�͂��_�d�ׂ����d�E�̌����ƍ����Ă��邩�H����Ă��邩�H������������ł��B
�i1�j�Ɠ����悤�ɁA�����Ă��镶�͂����̂܂��ŏ����Ă݂܂��傤�B
�_�d�ׂ����d�E�� $E$�A�_�d�ׂ̓d�C�ʂ� $q$�A������ $r$�A���萔�� $k$ �Ƃ���ƁA��蕶�ɏ�����Ă���Ӗ��̎��͎��̂悤�ɂȂ�܂��B
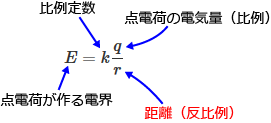
���̎��͓_�d�ׂ����d�E�̌����ɂȂ��Ă���ł��傤���H
�_�d�ׂ����d�E�̌����́A
$E=k\dfrac{q}{r^2}$�@�ł���ˁH
��蕶�̈Ӗ��̎��Ɠ_�d�ׂ����d�E�̌���������ׂ�ƁA�E�ӂ̕��ꂪ����Ă��āA��蕶�̈Ӗ��̎��̕���������1��ɔ�������A�_�d�ׂ����d�E�̌����̕���������2��ɔ�����ɂȂ��Ă��܂��B�i�ǂ���������ł����A1���2�悪�Ⴂ�܂��B�j
�Ȃ̂ŁA���́i2�j�̕��͂͊Ԉ���Ă��邱�ƂɂȂ�܂��B
�i3�j�d�C�͐��̐ڐ��̕����Ɠd�E�̕����Ɋւ�����
��蕶�̋L�q�i3�j
�d�C�͐���̔C�ӂ̓_�ł̐ڐ��̕����́A���̓_�̓d�E�̕����Ɉ�v����B
�i3�j�́u�d�C�͐��̐ڐ��̕����v���u�d�E�̕����v�ƈ�v���邩�H���Ȃ����H������������ł��B
�d�C�͐����ĉ��ł����H
�d�C�͐��̐ڐ��̕����Ɠd�E�̕������ē����ł����H�Ⴂ�܂����H
�݂����Ȗ��ł��B
���̂悤�Ȗ��̏ꍇ�́A���ۂɐ}�������Ċm�F���Ă݂�̂������ł���B
�ł͂܂��A���̓d�ׂƕ��̓d�ׂ���������āA�d�C�͐��������Ă݂܂��B����ƁA���̂悤�ɂȂ�܂��B
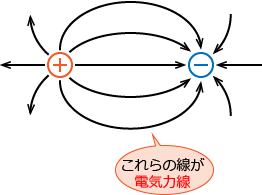
�d�C�͐��͐��̓d�ׂ���o�ĕ��̓d�ׂɌ��������ŁA�d�C�͐��͐��̓d�ׂ��琂���ɏo�ĕ��̓d�ׂɐ����ɓ���̂ŏ�̐}�̂悤�ɂȂ�܂��B
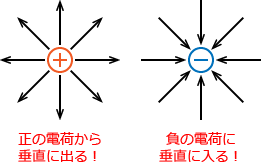
�d�C�͐����������̂ŁA���͓d�C�͐��̐ڐ��̕�����}�ɏ����Ă݂܂��B�ڐ��͐��ɐڂ�����Ȃ̂Ŏ��̐}�̂悤�ɂȂ�܂��B
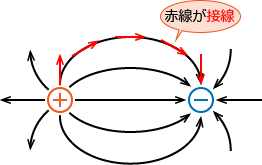
��̐}�ł͐ڐ��������Ă���̂łȂ�ł����A�ڐ���Z�������ƁA
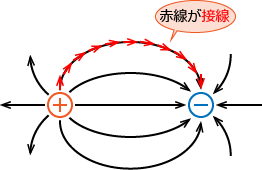
�ƂȂ��āA����ɖ������̂������Z�����āA�Ō�̂��Ƃ낾���ɖ��������Ɖ��̐}�̂悤�ɂȂ�܂��B�i�����Ă���Ӗ���������ƕ�����ɂ��������炲�߂�Ȃ����B�j
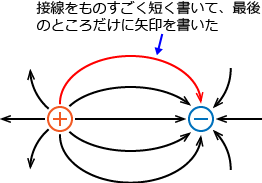
�Ȃ̂ŁA�u�d�C�͐��̐ڐ��̕����v���Ă����̂͋ɁX�Z���͈͂ōl����Ɓu�d�C�͐��̕����v�Ƃ������ƂȂ�ł��ˁB
����Ŗ�蕶�ɘb��߂��ƁA����i�d�C�͐��̐ڐ��̕����j���d�E�̕����Ɉ�v���邩�H�ł����A�d�E�̕������v���X����}�C�i�X�ɂȂ�̂ŁA�܂�u��v����v�ɂȂ�܂��B���������āA
�u�d�C�͐��̐ڐ������v�Ɓu�d�E�̕����v�͈�v�����@�c�i���j
�ƂȂ�A�i3�j�͐��������ƂɂȂ�܂��B
�i4�j���d�ʖʏ�̐��d�ׂɓ����N�[�����͂Ɋւ�����
��蕶�̋L�q�i4�j
���d�ʖʏ�̐��d�ׂɂ́A���̖ʂɉ����������ɐ��̃N�[�����͂������B
�i4�j���}�������čl���Ă݂܂��傤�B
���d�ׂ���u���ē��d�ʖʂ������Ă݂܂��B���d�ʖʂ͓d�ʂ��������ʂŁA�d�C�͐��Ɛ����ɂȂ�̂Ŏ��̐}�̂悤�ɂȂ�܂��B
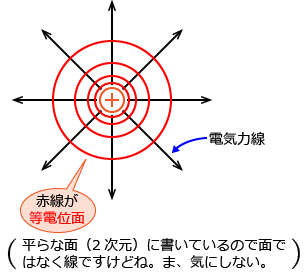
����Ŗ�蕶�i4�j�ɂ́u���d�ʖʏ�̐��d�ׂɂ́A���̖ʂɉ����������ɐ��̃N�[�����͂������B�v�Ə����Ă���܂����A���̈Ӗ��́A�u���d�ʖʏ�ɐ��d�ׂ�u�����瓙�d�ʖʂɉ����Đ��d�ׂ������B�v�Ƃ����Ӗ��ł��B�����}�ɏ����Ă݂�ƁA���̂悤�ɂȂ�܂��B
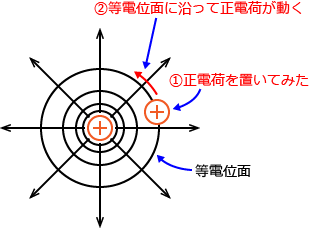
������ĈႢ�܂���ˁH
�}���S�`���S�`�����Ă���ƕ�����ɂ����̂ŁA���d�ׂ����̐}�ɂ��Ă݂܂��B

����ƁA���d�ׂ�������Ȃ̂ł����͂��݂��ɔ�����������ɓ����܂��B�����̐��d�ׂ͌Œ肳��ē����Ȃ��Ƃ���ƉE���̐��d�ׂ͎��̐}�̂悤�ɓ����܂���ˁH

�Ȃ̂ŁA��蕶�̋L�q�͊Ԉ���Ă��邱�ƂɂȂ�܂��B
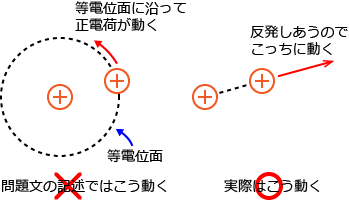
�i�d�ׂɓ����́i�N�[�����́j�̕����ɂ��Ă���������Əڂ����m�肽�������N�[�����̖@���̃y�[�W���Q�l�ɂ��Ă݂Ă��������B�j
�i5�j�Ód�e�ʁA�d�ɔԂ̓d�E�A�U�d���Ɋւ�����
��蕶�̋L�q�i5�j
�R���f���T�̓d�ɔԂɂ����ԂȂ��U�d�̂�����ƁA�Ód�e�ʂƓd�ɔԂ̓d�E�́A�U�d�̗̂U�d���ɔ�Ⴕ�đ��傷��B
�i5�j�̖�蕶�͓�ɕ����Ĉ���l���Ă����܂��傤�B
�R���f���T�̓d�ɔԂɂ����ԂȂ��U�d�̂�����ƁA�Ód�e�ʂ́A�U�d�̗̂U�d���ɔ�Ⴕ�đ��傷��A�Ȃ́H
����́A�R���f���T�̐Ód�e�ʂ̌�����������ΊȒP�ɕ�����܂��ˁB�R���f���T�̐Ód�e�ʂ̌����́A�R���f���T�̐Ód�e�ʂ� $C$�A�U�d�̗̂U�d���� $\varepsilon$�A�d�ɔʐς� $S$�A�d�ɔԊu�� $d$ �Ƃ���ƁA
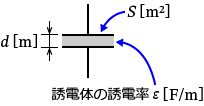
$C=\varepsilon\dfrac{S}{d}$�@�ɂȂ�܂��B
���̎����݂�ƁA�U�d�̗̂U�d�� $\varepsilon$ ���傫���Ȃ�ƐÓd�e�� $C$ ���傫���Ȃ�̂ŁA����́u���傷��v�Ő������ł��ˁB
�ł́A�������Ă݂܂��傤�B
�R���f���T�̓d�ɔԂɂ����ԂȂ��U�d�̂�����ƁA�d�ɔԂ̓d�E�́A�U�d�̗̂U�d���ɔ�Ⴕ�đ��傷��A�Ȃ́H
����́A�d�����x�Ɠd�E�̊W��\�킵�������ōl���Ă݂܂��傤�B
�d�����x�� $D$�A�U�d�̗̂U�d���� $\varepsilon$�A�d�ɔԂ̓d�E�� $E$ �Ƃ���ƁA
$D=\varepsilon\, E$�@�c�@�@�ł��ˁB
����Ň@���� $E=\cdots$ �ɒ����Ǝ��̎��ɂȂ�܂��B
$E=\dfrac{D}{\varepsilon}$
���̎����݂�ƁA�U�d�̗̂U�d�� $\varepsilon$ ���傫���Ȃ�Ɠd�ɔԂ̓d�E $E$ �͏������Ȃ�̂ŁA����́u���傷��v�͊Ԉ���Ă��邱�ƂɂȂ�܂��B
�i5�j�̖�蕶�́A�Ód�e�ʂɂ��Ă��������L�q�ł����A�d�ɔԂ̓d�E�ɂ��Ă��Ԉ�����L�q�ɂȂ��Ă���̂ŁA���́i5�j�͊Ԉ���Ă��邱�ƂɂȂ�܂��B
���̖��̂悤�ɁA�d���O��̐����₤���ł͕Е��͍����Ă��Ă��A�����Е��ɂ��Ă͊Ԉ���Ă���ꍇ������̂ŁA���������ۂ͋C��t����悤�ɂ��܂��傤�B
���̖����������߂Ɏg��������
�N�[�����̖@���̌����F$F=k\dfrac{q_1\, q_2}{r^2}$
�_�d�ׂ����d�E�̌����F$E=k\dfrac{q}{r^2}$
�R���f���T�̐Ód�e�ʂ̌����F$C=\varepsilon\dfrac{S}{d}$
�d�����x�Ɠd�E�̌����F$D=\varepsilon\, E$
���̖��ł��d�����x�̌������g���Ă��܂��B�d�����x�̌�����Y��Ă���l�������ł����A�d���O��̗��_�̖��������Ƃ��ɂ悭�g����̂ł��ڂ��Ă����悤�ɂ��܂��傤�B
�X�|���T�[�����N
�X�|���T�[�����N
�������߂��d���O��̉ߋ����W�͂������A�d���O��̎Q�l���͂������A�d���O��p�̐��w�Q�l���͂������ŏЉ�Ă��܂��̂ŎQ�l�ɂ��Ă݂Ă��������B
�X�|���T�[�����N
�d���O��u���_�v����21�N�x ��2�̉ߋ���Ɖ���@�֘A�y�[�W
- �d���O��u���_�v����21�N�x ��1�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��1�̉ߋ���Ɖ���ł��B���̉ߋ���͓d���A�d�E�A�R���f���T�Ɋւ����{�I�Ȍ�����������Ή�������ł��B
- �d���O��u���_�v����21�N�x ��3�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��3�̉ߋ���Ɖ���ł��B���̉ߋ���̓R�C���̎������𐔂ƃR�C���ɒ~�����鎥�C�G�l���M�[�Ɋւ�����ł��B
- �d���O��u���_�v����21�N�x ��4�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��4�̉ߋ���Ɖ���ł��B���̉ߋ���͐�`�����ɗ����d���ɂ�����鎥�E�Ɋւ�����ł��B�d���O��ł悭�o�肳��₷���p�^�[���̖��ł��B
- �d���O��u���_�v����21�N�x ��5�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��5�̉ߋ���Ɖ���ł��B���̉ߋ���̓R���f���T������E����ڑ��A�d��������E����ɐڑ�����Ă���Ƃ��̓d�E�̃G�l���M�[�i�Ód�G�l���M�[�j�����߂���ł��B
- �d���O��u���_�v����21�N�x ��6�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��6�̉ߋ���Ɖ���ł��B���̉ߋ���͒�R������ڑ��A����ڑ����ꂽ������H�̊�{�I�Ȗ��ŁA�^����ꂽ�d���E�d���̉�H���������R�l�����߂���ł��B�����ł̓L���q�z�b�t�̖@�����g���ĉ����Ă��܂��B
- �d���O��u���_�v����21�N�x ��7�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��7�̉ߋ���Ɖ���ł��B���̉ߋ���͒P��3�����𗬉�H�̌v�Z���ŁA3���ɗ����e���d���̑傫���̑召�W�����߂���ł��B�d�����Ɋe���ׂɗ����d�������߁A�L���q�z�b�t�̖@���i�d�����j��K�p���Ċe���d�������߂܂��B
- �d���O��u���_�v����21�N�x ��8�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��8�̉ߋ���Ɖ���ł��B���̉ߋ���͒P���𗬉�H�̌v�Z���ŁA�X�C�b�`S���J���Ă���Ƃ��ƕ��Ă���Ƃ��̂��ꂼ��̓d���̔�ƈʑ����̍������߂���ł��B�X�C�b�`S���J���Ă���Ƃ��ƕ��Ă���Ƃ��ŕ����Čv�Z���Ă����܂��B
- �d���O��u���_�v����21�N�x ��9�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��9�̉ߋ���Ɖ���ł��B���̉ߋ���͐����g�𗬓d���Ɋւ�����ŁA�d���̏u���l������l�ɂȂ�Ƃ��̎��������߂���ł��B�d�C�̖��ƌ��������A�قڐ��w�̖��ɋ߂��ł��B


