�X�|���T�[�����N
�d���O��u���_�v����21�N�x ��9�̉ߋ���Ɖ��
���y�[�W����PR��L�����܂܂��ꍇ������܂��B
�d���O��u���_�v����21�N�x��9�̉ߋ���̉���ł��B
�d���O��u���_�v����21�N�x�i2009�N�x�j�@��9
�d���O��u���_�v�̕���21�N�x��9�iA���j�̖��ł��B
���̖����������߂̃|�C���g
���̖����������߂̃|�C���g�́A
- �^����ꂽ�d���̎��̈Ӗ��͕�����܂����H�@�O���t�͏����܂����H
- $\sin$ �̕���������p�x�����߂��܂����H
- ��蕶�ɉ��́u���߂āv�Ə�����Ă���̂ł��傤���H
�ł��B
�X�|���T�[�����N
�X�|���T�[�����N
�d���O��u���_�v����21�N�x�i2009�N�x�j�@��9�iA���j�̉��
���̉ߋ���͐����g�𗬓d���ɂ��Ă̖��ŁA�d���̏u���l������l�i���̏ꍇ $4\,\mathrm{A}$�j�ɂȂ�Ƃ��̎��������߂���ł��B�d�C�̖��Ƃ��������A�قڐ��w�̖��ł��ˁB
�܂��A���̓d���̎��͂ǂ�Ȏ��Ȃ̂��H�@�l���Ă݂܂��傤�B
�����g�𗬓d�� $i$ �̎��i�u���l�̎��j�́A�ő�l�� $I_m$ �A�p���g���� $\omega$�A�ʑ��� $\theta$ �Ƃ���ƁA���̂悤�Ȏ��ŕ\�킳��܂���ˁH
$i=I_m\sin\left(\omega t+\theta\right)$�@�c�@
���̇@���Ɩ��ŗ^�����Ă���d���̎�������ׂĂ݂�ƁA���̂悤�ɑΉ����Ă��܂��B
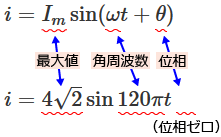
�Ȃ̂ŁA���ŗ^�����Ă���d���́A�ő�l�� $4\sqrt{2}$�A�p���g���� $120\pi$�i�u$\pi$�v���ăp�C�ł��j�A�ʑ��� $0$�i�[���j�̐����g�𗬓d���Ƃ������ƂɂȂ�܂��B
�ł́A�d���̃O���t�������Ă݂܂��傤�B�O���t�������Ă݂�Ǝ��̂悤�ɂȂ�܂��B
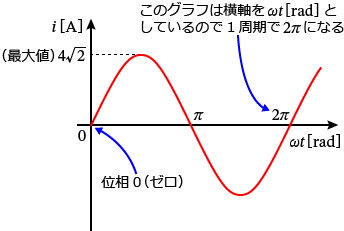
����Ŗ��́A�u$4\,\mathrm{A}$ �ɂȂ鎞���́H�v�Ȃ̂ŁA��̃O���t�œd���� $4\,\mathrm{A}$ �ɂȂ�Ƃ���̎���������������Ƃ������Ƃł��ˁB�O���t�� $4\,\mathrm{A}$ �̐��������Ă݂܂��傤�B
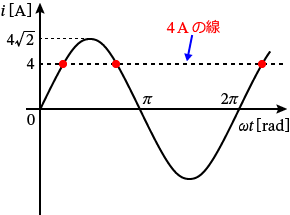
��������ƁA�d���� $4\,\mathrm{A}$ �ɂȂ�Ƃ��낪��̃O���t�̐Ԃ��ۂɂȂ�A���̐Ԃ��ۂ̂Ƃ���̎����� $4\,\mathrm{A}$ �ɂȂ鎞���ɂȂ�܂���ˁH
���̐Ԃ��ۂ̂Ƃ���̎��������߂�Γd���� $4\,\mathrm{A}$ �ɂȂ鎞�������߂��܂����A�����g�͓����g�`���J��Ԃ����̂ŁA���̐Ԃ��ۂ͂��`���Ɠ����悤�ɑ����Ă����܂��B
����ƁA���߂铚�������ς����肻���ł����A��蕶�ɂ́u���� $t=0$�m$\mathrm{s}$�n�ȍ~�ɏ��߂� $4\,\mathrm{A}$ �ɂȂ鎞���́H�v�Ə����Ă���̂ŁA���߂鎞���͏��߂̐Ԃ��ۂ̎��������Ƃ������ƂɂȂ�܂��B
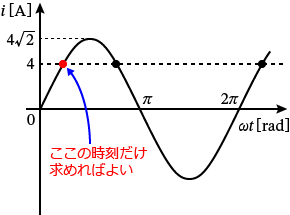
�ł́A���߂� $4\,\mathrm{A}$ �ɂȂ�Ƃ��̎��������߂Ă݂܂��傤�B���������߂邽�߂ɂ́A�^����ꂽ�d���̎��� $i=4\,\mathrm{A}$ �������Ď��� $t_1$ �����߂�����ł��B�d���̎��� $i=4\,\mathrm{A}$ ��������ƁA
$4=4\sqrt{2}\sin 120\pi t_1$
�ƂȂ�̂ŁA����� $t_1$ �ɂ��ĉ����܂��傤�B
$1=\sqrt{2}\sin 120\pi t_1$�@�A�@$\sin 120\pi t_1=\dfrac{1}{\sqrt{2}}$�@�A�@$120\pi t_1=\sin^{-1}\dfrac{1}{\sqrt{2}}$�@�c�A
$\sin\theta$ �� $\dfrac{1}{\sqrt{2}}$ �ɂȂ�̂́A$\dfrac{\pi}{4}$�A$\dfrac{3\pi}{4}$�A$\dfrac{9\pi}{4}$�A�c�ł����A��蕶�ɏ�����Ă�������u���߂āv���A�A���́A
$120\pi t_1=\dfrac{\pi}{4}$�@�ƂȂ�܂��B�v�Z�𑱂���ƁA
$t_1=\dfrac{\pi}{120\pi\times 4} =\dfrac{1}{120\times 4} =\dfrac{1}{480}$
$\therefore t_1=\dfrac{1}{480}$�@�m$\mathrm{s}$�n�@�c�i���j
�ƂȂ�A�����́i1�j�ɂȂ�܂��B
���̖����������߂Ɏg��������
�����g�𗬓d���̌����F$i=I_m\sin\left(\omega t+\theta\right)$
�O�p���̌����i$\sin$�j�F$\sin\theta =\dfrac{b}{c}$
�p�x�����߂�����i$\sin$�j�F$\theta =\sin^{-1}\dfrac{b}{c}$
�����g�𗬓d���̃O���t�ɂ���
���̃y�[�W�̉���̐����g�𗬓d���̃O���t�́A������ $\omega t$�m$\mathrm{rad}$�n�Ƃ��Ă��܂����A���������� $t$�m$\mathrm{s}$�n�Ƃ��ď������Ƃ��ł��܂��B
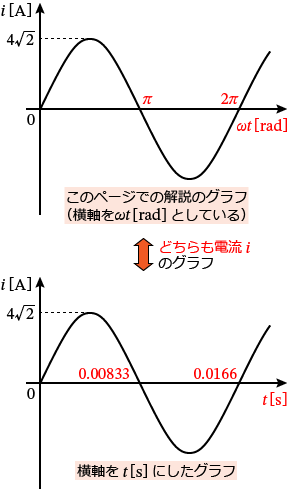
�������A�����̕����ʁi���W�A���i$\mathrm{rad}$�j���H�@�b���H�j���قȂ�̂ŁA�����̒l���قȂ邱�Ƃɒ��ӂ��܂��傤�B
���Ȃ݂ɁA1�����i$2\pi$�j�̂Ƃ�������Ԃɒ����ƁA
$120\pi t=2\pi$ ���A$t=\dfrac{2\pi}{120\pi} =\dfrac{1}{60} =0.0166\cdots$�m$\mathrm{s}$�n �ƂȂ�܂��B
���̓d���̎��̎��g���͉�Hz�H
���ŗ^�����Ă��鐳���g�𗬓d���̊p���g�� $\omega$ �͎����A$\omega =120\pi$ �ł��ˁB
����ƁA�p���g���Ǝ��g���̊W�� $\omega =2\pi f$ ���A$2\pi f=120\pi$ �Ȃ̂ŁA
$\therefore f=\dfrac{120\pi}{2\pi} =60$�@�m$\mathrm{Hz}$�n�@�ƂȂ�܂��B
�Ȃ̂ŁA���ŗ^�����Ă���d���́A�����{�̓d���̎��g�� $60\,\mathrm{Hz}$ �Ɠ����Ƃ������ƂɂȂ�܂��B
�����g�𗬂̎��ƃO���t�͐����g�𗬉�H���l����Ƃ��̊�{�Ȃ̂ŁA���̈Ӗ������ڂ��A�O���t��������悤�ɂ��Ă����܂��傤�B
�X�|���T�[�����N
�X�|���T�[�����N
�������߂��d���O��̉ߋ����W�͂������A�d���O��̎Q�l���͂������A�d���O��p�̐��w�Q�l���͂������ŏЉ�Ă��܂��̂ŎQ�l�ɂ��Ă݂Ă��������B
�X�|���T�[�����N
�d���O��u���_�v����21�N�x ��9�̉ߋ���Ɖ���@�֘A�y�[�W
- �d���O��u���_�v����21�N�x ��1�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��1�̉ߋ���Ɖ���ł��B���̉ߋ���͓d���A�d�E�A�R���f���T�Ɋւ����{�I�Ȍ�����������Ή�������ł��B
- �d���O��u���_�v����21�N�x ��2�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��2�̉ߋ���Ɖ���ł��B���̉ߋ���͐Ód�E�Ɋւ����{�I�Ȓm���̐����₤���ł��B
- �d���O��u���_�v����21�N�x ��3�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��3�̉ߋ���Ɖ���ł��B���̉ߋ���̓R�C���̎������𐔂ƃR�C���ɒ~�����鎥�C�G�l���M�[�Ɋւ�����ł��B
- �d���O��u���_�v����21�N�x ��4�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��4�̉ߋ���Ɖ���ł��B���̉ߋ���͐�`�����ɗ����d���ɂ�����鎥�E�Ɋւ�����ł��B�d���O��ł悭�o�肳��₷���p�^�[���̖��ł��B
- �d���O��u���_�v����21�N�x ��5�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��5�̉ߋ���Ɖ���ł��B���̉ߋ���̓R���f���T������E����ڑ��A�d��������E����ɐڑ�����Ă���Ƃ��̓d�E�̃G�l���M�[�i�Ód�G�l���M�[�j�����߂���ł��B
- �d���O��u���_�v����21�N�x ��6�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��6�̉ߋ���Ɖ���ł��B���̉ߋ���͒�R������ڑ��A����ڑ����ꂽ������H�̊�{�I�Ȗ��ŁA�^����ꂽ�d���E�d���̉�H���������R�l�����߂���ł��B�����ł̓L���q�z�b�t�̖@�����g���ĉ����Ă��܂��B
- �d���O��u���_�v����21�N�x ��7�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��7�̉ߋ���Ɖ���ł��B���̉ߋ���͒P��3�����𗬉�H�̌v�Z���ŁA3���ɗ����e���d���̑傫���̑召�W�����߂���ł��B�d�����Ɋe���ׂɗ����d�������߁A�L���q�z�b�t�̖@���i�d�����j��K�p���Ċe���d�������߂܂��B
- �d���O��u���_�v����21�N�x ��8�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��8�̉ߋ���Ɖ���ł��B���̉ߋ���͒P���𗬉�H�̌v�Z���ŁA�X�C�b�`S���J���Ă���Ƃ��ƕ��Ă���Ƃ��̂��ꂼ��̓d���̔�ƈʑ����̍������߂���ł��B�X�C�b�`S���J���Ă���Ƃ��ƕ��Ă���Ƃ��ŕ����Čv�Z���Ă����܂��B


