�X�|���T�[�����N
�d���O��u���_�v����21�N�x ��4�̉ߋ���Ɖ��
���y�[�W����PR��L�����܂܂��ꍇ������܂��B
�d���O��u���_�v����21�N�x��4�̉ߋ���̉���ł��B
�d���O��u���_�v����21�N�x�i2009�N�x�j�@��4
�d���O��u���_�v�̕���21�N�x��4�iA���j�̖��ł��B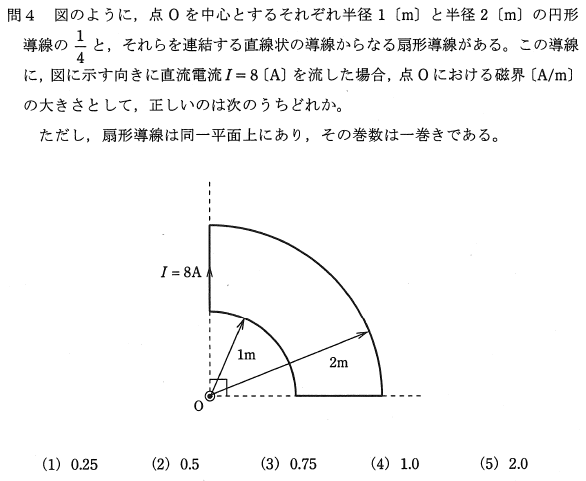
���̖����������߂̃|�C���g�ƃR�c
���̖����������߂̃|�C���g�ƃR�c�́A
- �d��������铱���̊e�������ɕ����čl���悤�I
- ������̓����̉�����̎��E�̑傫���͂ǂ��Ȃ�́H
- �d���Ǝ��E�Ɋւ����{�I�Ȍ����͕�����܂����H
- �~�`�R�C�������S�ȉ~�ɂȂ��Ă��Ȃ��ꍇ�A�~�̒��S�ɍ���鎥�E�̑傫���͂ǂ��Ȃ�́H
- ���E�̓x�N�g���Ȃ̂Ō���������܂���I
�ł��B
�X�|���T�[�����N
�X�|���T�[�����N
�d���O��u���_�v����21�N�x�i2009�N�x�j�@��4�iA���j�̉��
���̉ߋ���́A��`�����ɒ����d��������Ă���Ƃ��ɁA���̐�`�̒��S�i��`�����~�ʂ̒��S�j�ɍ���鎥�E�̑傫���͂����炩�H�@�Ƃ������ł��B
����Ȋ����̖��͓d���O��̗��_�ł悭�o�肳��Ă��܂����A�������͂ǂ̖����قړ����ł��B�Ȃ̂ŁA�������̗����K�����ڂ��Ă����悤�ɂ��܂��傤�B
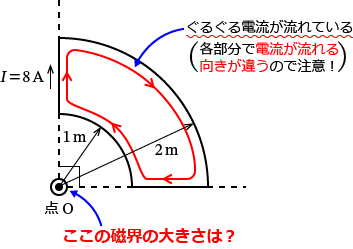
���̖��̉������Ƃ��ẮA��`������4�̕����ɕ����A���������ꂼ��̕����ɗ����d���ɂ��_ $\mathrm{O}$ �ɍ���鎥�E�����߁A�����̎��E�̃x�N�g���a�����߂�����ł��B
���Ȃ�������ɂ������͂ɂȂ��Ă܂��H�@�܂�A�����������Ƃł��B
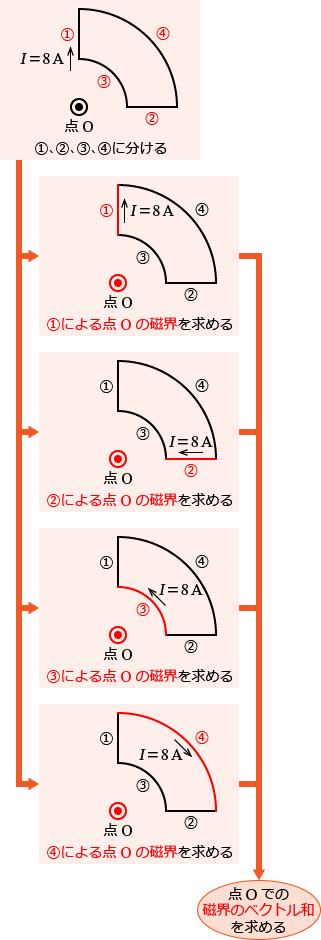
�@�A�A�A�B�A�C���ꂼ��Ɨ��ɍl���Čv�Z���Ă��������ł��B
�ł́A�@�̕����ɗ����d�����_ $\mathrm{O}$ �ɍ�鎥�E���狁�߂Ă݂܂��傤�B
�@�̕����ɗ����d�����_O�ɍ�鎥�E
�@�̕����Ɠ_ $\mathrm{O}$ �����̐}�������Ǝ��̂悤�ɂȂ�܂��B
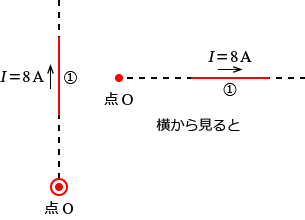
�@�Ɠ_ $\mathrm{O}$ �̈ʒu�W�́A����ʏ�ɂ����ć@�̐��������������Ƃ���ɓ_ $\mathrm{O}$ ������܂���ˁH
���̂悤�ȏꍇ�́A�@�̕����ɗ����d���ɂ���ē_ $\mathrm{O}$ �ɂ͎��E������܂���B�i���̗��R�̓r�I�E�T�o�[���̖@���ɂ������ł��܂����A�d���O��ł͂����܂ł̒m���͕K�v�Ȃ��ł���H�Ǝ��͏���Ɏv���̂ŁA�����ł͐����͏ȗ��B�j
�Ȃ̂ŁA�@�̕����ɗ����d�����_ $\mathrm{O}$ �ɍ�鎥�E�̑傫���� $H_1$ �Ƃ���ƁA
$\therefore H_1=0$�@�m$\mathrm{A/m}$�n�@�c�D�@�ƂȂ�܂��B
�A�̕����ɗ����d�����_O�ɍ�鎥�E
�A�̕����Ɠ_ $\mathrm{O}$ �����̐}�������Ǝ��̂悤�ɂȂ�܂��B
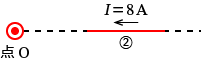
���̏ꍇ���@�Ɠ����悤�ɇA�Ɠ_ $\mathrm{O}$ �̈ʒu�W�́A����ʏ�ɂ����ćA�̕��������������Ƃ���ɓ_ $\mathrm{O}$ ������܂��B
�Ȃ̂Ň@�Ɠ��l�ɁA�A�̕����ɗ����d�����_ $\mathrm{O}$ �ɍ�鎥�E�̑傫���� $H_2$ �Ƃ���ƁA
$\therefore H_2=0$�@�m$\mathrm{A/m}$�n�@�c�E�@�ƂȂ�܂��B
�B�̕����ɗ����d�����_O�ɍ�鎥�E
�B�̕����Ɠ_ $\mathrm{O}$ �����̐}�������Ǝ��̂悤�ɂȂ�܂��B
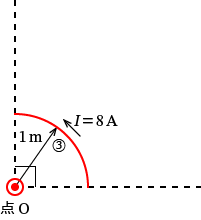
���̂悤�ɉ~�� $\dfrac{1}{4}$ �̉~�ʂƂ����~�̏ꍇ�ɂ́A������ƈ�������~�ɗ����d���ɂ�����鎥�E�����߁A$\dfrac{1}{4}$ �̉~�ʂ̏ꍇ�ɂ͂���� $\dfrac{1}{4}$�A���~�̏ꍇ�ɂ͂���� $\dfrac{1}{2}$ ���Ď��E�����߂܂��B
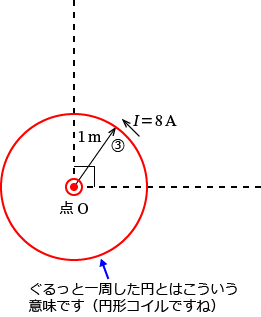
������ƈ�������~�ɗ����d���ɂ��_ $\mathrm{O}$ �ɍ���鎥�E�̑傫���� $H_{30}$ �Ƃ���ƁA�~�`�R�C���ɗ����d���ɂ��~�̒��S�̎��E�̌������A
$H_{30}=\dfrac{I}{2r} =\dfrac{8}{2\times 1} =\dfrac{8}{2} =4$�@�c�F
�B�̕����� $\dfrac{1}{4}$ �̉~�ʂȂ̂ŇF�� $\dfrac{1}{4}$ ���܂��B����ƁA���߂����B�̕����ɗ����d�����_ $\mathrm{O}$ �ɍ�鎥�E�̑傫�� $H_3$ �́A
$H_3=H_{30}\times\dfrac{1}{4} =4\times\dfrac{1}{4} =1$
$\therefore H_3=1$�@�m$\mathrm{A/m}$�n�@�c�G�@�ƂȂ�܂��B
�C�̕����ɗ����d�����_O�ɍ�鎥�E
�C�̕����Ɠ_ $\mathrm{O}$ �����̐}�������Ǝ��̂悤�ɂȂ�܂��B
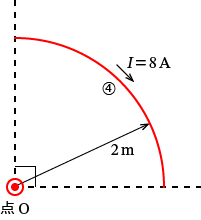
���̏ꍇ���B�Ɠ����悤�ɋ��߂܂��B
������ƈ�������~�ɗ����d���ɂ��_ $\mathrm{O}$ �ɍ���鎥�E�̑傫���� $H_{40}$ �Ƃ���ƁA�~�`�R�C���ɗ����d���ɂ��~�̒��S�̎��E�̌������A
$H_{40}=\dfrac{I}{2r} =\dfrac{8}{2\times 2} =\dfrac{8}{4} =2$�@�c�H
�C�̕����� $\dfrac{1}{4}$ �̉~�ʂȂ̂ŇH�� $\dfrac{1}{4}$ ���܂��B����ƁA���߂����C�̕����ɗ����d�����_ $\mathrm{O}$ �ɍ�鎥�E�̑傫�� $H_4$ �́A
$H_4=H_{40}\times\dfrac{1}{4} =2\times\dfrac{1}{4} =\dfrac{1}{2} =0.5$
$\therefore H_4=0.5$�@�m$\mathrm{A/m}$�n�@�c�I�@�ƂȂ�܂��B
�ȏ���A�@�A�A�A�B�A�C�̕����ɗ����d�����ꂼ�ꂪ�_ $\mathrm{O}$ �ɍ�鎥�E�̑傫�������߂�ꂽ�̂ŁA���Ƃ̓x�N�g���a�����߂邾���ł��B
�����ł͂��ꂼ��̎��E�����߂�Ƃ��Ɏ��E�́u�傫���v�ŋ��߂��̂ŁA�x�N�g���a�����߂邽�߂ɂ͌������l���Ȃ���Ȃ�܂���B
�@�ƇA�̕����̎��E�̑傫���͂Ƃ��Ƀ[���Ȃ̂ŁA�@�ƇA�ɂ��Ă͓��ɍl����K�v�͂Ȃ��A�l���Ȃ���Ȃ�Ȃ��͇̂B�ƇC�̕����ł��B
�x�N�g���̐����������ʂ̗�����\�����Ƃ���ƁA�B�̕����ɗ����d�����_ $\mathrm{O}$ �ɍ�鎥�E�̌����͉E�˂��̖@����莆�ʂ̗�����\�����ɂȂ�܂��ˁB
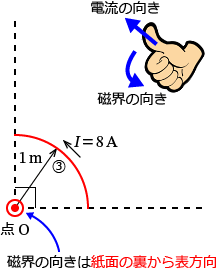
�܂�A���E $\boldsymbol{H_3}$ �̌����͐������i���ʂ̗�����\�����j�Ȃ̂ŇG���A
$\therefore \boldsymbol{H_3} =1$�@�m$\mathrm{A/m}$�n�@�c�J�@�ƂȂ�܂��B
���́A�C�̕����ɂ��Ăł��B
�C�̕����ɗ����d�����_ $\mathrm{O}$ �ɍ�鎥�E�̌����́A�E�˂��̖@����莆�ʂ̕\���痠�����ɂȂ�܂��B
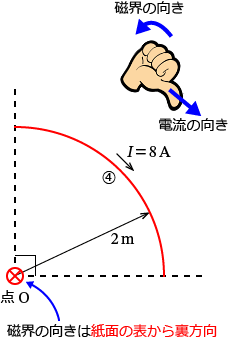
�Ȃ̂ŁA���E $\boldsymbol{H_4}$ �̌����͕������i���ʂ̕\���痠�����j�Ȃ̂ŇI���A
$\therefore \boldsymbol{H_4} =-0.5$�@�m$\mathrm{A/m}$�n�@�c�K�@�ƂȂ�܂��B�i$\boldsymbol{H_4}$ �͕������Ȃ̂Ń}�C�i�X�I�j
���Ƃ́A�J�ƇK�̃x�N�g���a�����߂�����ł��B
$\boldsymbol{H_3} +\boldsymbol{H_4} =1-0.5=0.5$
���������āA���߂�_ $\mathrm{O}$ �ɂ����鎥�E�̑傫���́A$0.5$�m$\mathrm{A/m}$�n�@�c�i���j�@�ƂȂ�܂��B
���̖����������߂Ɏg��������
�~�`�R�C���ɗ����d���ɂ��~�̒��S�̎��E�̌����F$H=\dfrac{I}{2r}$
�������ɂ���
���̃y�[�W�ł̉������́A���ꂼ��̎��E�̑傫�������߂Ă���Ō�ɂ��ꂼ��̎��E�̌����ɂ��čl���܂������A���߂���x�N�g���ōl���ĉ����Ă����Ă������ł���B
�������i�v�Z���@�j�͐F�X����̂ŁA�����ł��₷���Ƃ��A�ȒP���Ǝv���������ʼn����Ă����܂��傤�B
�E�˂��̖@���ɂ���
�E�˂��̖@���͓d���Ǝ��E�̌������l����Ƃ��̊�{�Ȃ̂ŁA�m���ɂ��ڂ��Ă����悤�ɂ��܂��傤�B�u���[��A�悭������Ȃ��I�v�Ƃ��������E�˂��̖@���̃y�[�W���Q�l�ɂ��Ă݂Ă��������B
�X�|���T�[�����N
�X�|���T�[�����N
�r�I�E�T�o�[���̖@���ɂ��Ă͂������ʼn�����Ă��܂��̂ŁA���E�̌����̓������Ȃǂ�����������͎Q�l�ɂ��Ă݂Ă��������B
�������߂��d���O��̉ߋ����W�͂������A�d���O��̎Q�l���͂������A�d���O��p�̐��w�Q�l���͂������ŏЉ�Ă��܂��̂ŎQ�l�ɂ��Ă݂Ă��������B
�X�|���T�[�����N
�d���O��u���_�v����21�N�x ��4�̉ߋ���Ɖ���@�֘A�y�[�W
- �d���O��u���_�v����21�N�x ��1�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��1�̉ߋ���Ɖ���ł��B���̉ߋ���͓d���A�d�E�A�R���f���T�Ɋւ����{�I�Ȍ�����������Ή�������ł��B
- �d���O��u���_�v����21�N�x ��2�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��2�̉ߋ���Ɖ���ł��B���̉ߋ���͐Ód�E�Ɋւ����{�I�Ȓm���̐����₤���ł��B
- �d���O��u���_�v����21�N�x ��3�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��3�̉ߋ���Ɖ���ł��B���̉ߋ���̓R�C���̎������𐔂ƃR�C���ɒ~�����鎥�C�G�l���M�[�Ɋւ�����ł��B
- �d���O��u���_�v����21�N�x ��5�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��5�̉ߋ���Ɖ���ł��B���̉ߋ���̓R���f���T������E����ڑ��A�d��������E����ɐڑ�����Ă���Ƃ��̓d�E�̃G�l���M�[�i�Ód�G�l���M�[�j�����߂���ł��B
- �d���O��u���_�v����21�N�x ��6�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��6�̉ߋ���Ɖ���ł��B���̉ߋ���͒�R������ڑ��A����ڑ����ꂽ������H�̊�{�I�Ȗ��ŁA�^����ꂽ�d���E�d���̉�H���������R�l�����߂���ł��B�����ł̓L���q�z�b�t�̖@�����g���ĉ����Ă��܂��B
- �d���O��u���_�v����21�N�x ��7�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��7�̉ߋ���Ɖ���ł��B���̉ߋ���͒P��3�����𗬉�H�̌v�Z���ŁA3���ɗ����e���d���̑傫���̑召�W�����߂���ł��B�d�����Ɋe���ׂɗ����d�������߁A�L���q�z�b�t�̖@���i�d�����j��K�p���Ċe���d�������߂܂��B
- �d���O��u���_�v����21�N�x ��8�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��8�̉ߋ���Ɖ���ł��B���̉ߋ���͒P���𗬉�H�̌v�Z���ŁA�X�C�b�`S���J���Ă���Ƃ��ƕ��Ă���Ƃ��̂��ꂼ��̓d���̔�ƈʑ����̍������߂���ł��B�X�C�b�`S���J���Ă���Ƃ��ƕ��Ă���Ƃ��ŕ����Čv�Z���Ă����܂��B
- �d���O��u���_�v����21�N�x ��9�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��9�̉ߋ���Ɖ���ł��B���̉ߋ���͐����g�𗬓d���Ɋւ�����ŁA�d���̏u���l������l�ɂȂ�Ƃ��̎��������߂���ł��B�d�C�̖��ƌ��������A�قڐ��w�̖��ɋ߂��ł��B


