�X�|���T�[�����N
�d���O��u���_�v����21�N�x ��6�̉ߋ���Ɖ��
���y�[�W����PR��L�����܂܂��ꍇ������܂��B
�d���O��u���_�v����21�N�x��6�̉ߋ���̉���ł��B
�d���O��u���_�v����21�N�x�i2009�N�x�j�@��6
�d���O��u���_�v�̕���21�N�x��6�iA���j�̖��ł��B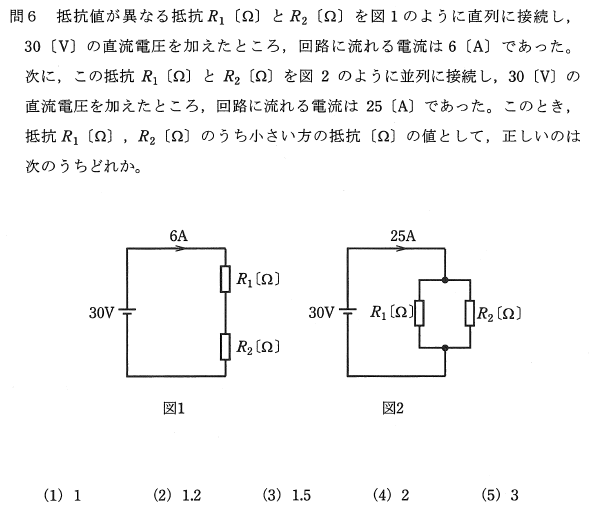
���̖����������߂̃|�C���g�ƃR�c
���̖����������߂̃|�C���g�ƃR�c�́A
- ������H�̌v�Z�����邽�߂̊�{�I�Ȗ@���i���̃y�[�W�ł̉������̏ꍇ�A�I�[���̖@���A�L���q�z�b�t�̖@���j�͕�����܂����H
- �������̉������͕�����܂����H
- ������H�̌v�Z������Ƃ��͕�����Ƃ��납�狁�߂Ă������I
�ł��B
�X�|���T�[�����N
�X�|���T�[�����N
�d���O��u���_�v����21�N�x�i2009�N�x�j�@��6�iA���j�̉��
���̉ߋ���͒�����H�ɂ��Ă̖��ŁA���ŗ^���炦���������疢�m���̒�R $R_1$�A$R_2$ �����߂���ł��B
������H�̌v�Z�Ɍ��炸�d�C��H�̌v�Z������Ƃ��ɂ́A�^����ꂽ�����i�������Ă�������j�Ɠd�C�̐F�X�Ȗ@�����g���āA������Ƃ��납�狁�߂Ă��������ł��B
�ł́A�^����ꂽ�����Ɠd�C�̖@�����g���Ē�R $R_1$ �� $R_2$ �����߂Ă݂܂��傤�I�@�܂��͈�ڂ̏����i�}1�j����ł��B
��蕶��ǂ�ł݂�ƁA
�u��R $R_1$�m$\Omega$�n�� $R_2$�m$\Omega$�n��}1�̂悤�ɒ���ɐڑ����A$30$�m$\mathrm{V}$�n�̒����d�����������Ƃ���A��H�ɗ����d���� $6$�m$\mathrm{A}$�n�ł������B�v
�Ə����Ă���܂��B
����Ő}1�͎��̂悤�ȉ�H�}�ł��ˁB
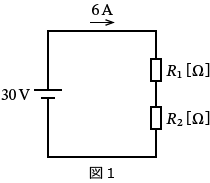
�}1�́A�u��R $R_1$ �� $R_2$ ������ɐڑ�����Ă��āA����� $30\,\mathrm{V}$ �̓d�������������H�� $6\,\mathrm{A}$ �̓d�������ꂽ�B�v�Ƃ����Ӗ��ł��ˁB�i���ꂪ�^����ꂽ�����ɂȂ�܂��B�j
�d�C��H�̌v�Z���@�ɂ͐F�X����A���̖����������������F�X����܂����A�����ł̓L���q�z�b�t�̖@�����g���ĉ����Ă݂悤�Ǝv���܂��B
���ƁA���̑O�ɃI�[���̖@�����g���Ē�R $R_1$ �� $R_2$ �ɂ�����d�� $V_1$�A$V_2$ �����߂Ă����܂��傤�B
��R $R_1$ �� $R_2$ �ɗ����d���͂ǂ���� $6\,\mathrm{A}$ �Ȃ̂ŁA�I�[���̖@�����A
��R $R_1$ �ɂ�����d�� $V_1$ �́A$V_1=6R_1$�m$\mathrm{V}$�n
��R $R_2$ �ɂ�����d�� $V_2$ �́A$V_2=6R_2$�m$\mathrm{V}$�n
�ɂȂ�܂��B
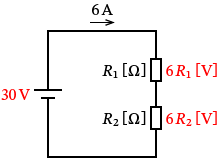
�Ȃ̂ŁA�L���q�z�b�t�̑��@���i�d�����j��K�p����ƁA
$30=6R_1+6R_2$
���ӂ� $6$ �Ŋ����āA
$\therefore R_1+R_2=5$�@�c�@�@�Ƃ�������������܂��B
�}1�ɂ��ẮA�����OK�ł��B
���͓�ڂ̏����i�}2�j�ɂ��Ăł��B
��蕶���܂��܂��ǂ�ł݂�ƁA
�u��R $R_1$�m$\Omega$�n�� $R_2$�m$\Omega$�n��}2�̂悤�ɕ���ɐڑ����A$30$�m$\mathrm{V}$�n�̒����d�����������Ƃ���A��H�ɗ����d���� $25$�m$\mathrm{A}$�n�ł������B�v
�Ə����Ă���܂��B
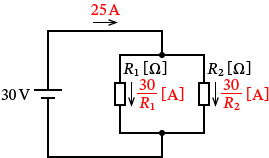
����Ő}2�͎��̂悤�ȉ�H�}�ł��ˁB
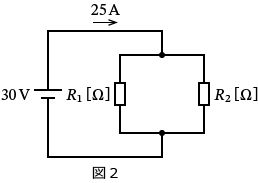
�}2�́A�u��R $R_1$ �� $R_2$ ������ڑ�����Ă��āA����� $30\,\mathrm{V}$ �̓d�������������H�� $25\,\mathrm{A}$ �̓d�������ꂽ�B�v�Ƃ����Ӗ��ł��ˁB�i���ꂪ�^����ꂽ�����ɂȂ�܂��B�j
�}2�ɂ��Ă��L���q�z�b�t�̖@�����g���܂����A���̑O�ɃI�[���̖@�����g���Ē�R $R_1$ �� $R_2$ �ɗ����d�� $I_1$�A$I_2$ �����߂Ă����܂��傤�B
��R $R_1$ �� $R_2$ �ɂ�����d���͂ǂ���� $30\,\mathrm{V}$ �Ȃ̂ŁA�I�[���̖@�����A
��R $R_1$ �ɗ����d�� $I_1$ �́A$I_1=\dfrac{30}{R_1}$�@�m$\mathrm{A}$�n
��R $R_2$ �ɗ����d�� $I_2$ �́A$I_2=\dfrac{30}{R_2}$�@�m$\mathrm{A}$�n
�ɂȂ�܂��B
�Ȃ̂ŁA�L���q�z�b�t�̑��@���i�d�����j��K�p����ƁA
$25=\dfrac{30}{R_1} +\dfrac{30}{R_2}$�@�A�@$5=\dfrac{6}{R_1} +\dfrac{6}{R_2}$�@�A�@$\dfrac{6R_2+6R_1}{R_1R_2} =5$
$\therefore 6R_1+6R_2=5R_1R_2$�@�c�A�@�Ƃ�������������܂��B
����ƁA�@���ƇA�������Ƃ��ł����̂ŁA�@���ƇA���̘A���������������Β�R $R_1$ �� $R_2$ �����߂邱�Ƃ��ł��܂��B
$\left\{\begin{array}{l} R_1+R_2=5 \quad\text{�c�@} \\ 6R_1+6R_2=5R_1R_2 \quad\text{�c�A} \end{array}\right.$
�@�����A$R_2=5-R_1$�@�c�B�@�Ȃ̂ŁA������A���ɑ�����܂��B
$6R_1+6\left( 5-R_1\right) =5R_1\left( 5-R_1\right)$
�����W�J���āA
$6R_1+30-6R_1=25R_1-5{R_1}^2$�@�A�@$30=25R_1-5{R_1}^2$
���ӂɑS�������Ă��� $\text{�E��} =0$ �̌`�ɂ���ƁA
$5{R_1}^2-25R_1+30=0$�@�A�@${R_1}^2-5R_1+6=0$�@�c�C
�����������������ƁA
$\left( R_1-2\right)\left( R_1-3\right) =0$�@�@���������āA
$\therefore R_1=2\,\Omega$�@�܂��́@$3\,\Omega$
��R $R_1$ �̒l��2���߂�ꂽ�̂ŁA���ꂼ��̂Ƃ��̒�R $R_2$ �̒l�����߂܂��B
�i�@�j$R_1=2\,\Omega$ �̂Ƃ�
$R_1=2$ ���B���ɑ�����܂��傤�B����ƁA
$R_2=5-2=3$
$\therefore R_2=3\,\Omega$
�i�A�j$R_1=3\,\Omega$ �̂Ƃ�
$R_1=3$ ���B���ɑ�����܂��傤�B����ƁA
$R_2=5-3=2$
$\therefore R_2=2\,\Omega$
���������āA���߂�ꂽ��R�̒l�̑g�����́A
��R $R_1=2\,\Omega$ �̂Ƃ���R $R_2=3\,\Omega$�@�܂��́A
��R $R_1=3\,\Omega$ �̂Ƃ���R $R_2=2\,\Omega$�@�ƂȂ�܂��B
���߂铚�͒�R $R_1$�m$\Omega$�n�A$R_2$�m$\Omega$�n�̂������������̒�R�m$\Omega$�n�̒l�Ȃ̂� $2\,\Omega$ �ƂȂ�A�i4�j�����ƂȂ�܂��B�@�c�i���j
���̖����������߂Ɏg��������
�I�[���̖@���̌����F$V=I\,R$�@�A�@$I=\dfrac{V}{R}$
�L���q�z�b�t�̖@���i�d�����j�̌����F$V=V_1+V_2$
�L���q�z�b�t�̖@���i�d�����j�̌����F$I=I_1+I_2$
�������̉��̋��ߕ�
��R $R_1$ �̒l�����߂�Ƃ��ɁA�����ł� $R_1$ �̓������i�C���j�������������ċ��߂܂������A�������̉��̌������g���ċ��߂Ă������ł��B
�������̉��̌����́A�������� $ax^2+bx+c=0$ �ŗ^����ꂽ�Ƃ��A
$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$�@�ł��ˁB
���Ȃ݂ɁA�C���i${R_1}^2-5R_1+6=0$�j�̉���������̉��̌������g���ċ��߂Ă݂�ƁA
$R_1$ $=\dfrac{-\left( -5\right)\pm\sqrt{\left( -5\right)^2 -4\times 1\times 6}}{2\times 1}$ $=\dfrac{5\pm\sqrt{25-24}}{2}$ $=\dfrac{5\pm\sqrt{1}}{2}$ $=\dfrac{5\pm 1}{2}$
$R_1=\dfrac{5+1}{2} =\dfrac{6}{2} =3$�@�@$\therefore R_1=3$
�܂��́A
$R_1=\dfrac{5-1}{2} =\dfrac{4}{2} =2$�@�@$\therefore R_1=2$�@�ƂȂ�܂��B
�������̉��̌����͂��ڂ��Ă����Ɖ����ƕ֗��Ȃ̂ŁA���ڂ��Ă��������������ł���B
�����ł̓I�[���̖@���ƃL���q�z�b�t�̖@�����g���ĉ����܂������A�}1�̒���ڑ����ꂽ��R�A�}2�̕���ڑ����ꂽ��R���ꂼ��̍�����R�����߂Ă�������Ă����v�Z���@������܂��B�F�X�Ȍv�Z���@�ʼn����Ă݂�Ǝ��̓A�b�v�ɂȂ���܂��̂ŁA���Ѓ`�������W���Ă݂܂��傤�I
�X�|���T�[�����N
�X�|���T�[�����N
�L���q�z�b�t�̖@���ɂ��Ă悭������Ȃ������L���q�z�b�t�̖@���̃y�[�W�A�I�[���̖@���ɂ��Ă悭������Ȃ������I�[���̖@���̃y�[�W���Q�l�ɂ��Ă݂Ă��������B������R�ɂ��ẮA�������������R�̃y�[�W���Q�l�ɂ��Ă݂Ă��������B�B
�������߂��d���O��̉ߋ����W�͂������A�d���O��̎Q�l���͂������A�d���O��p�̐��w�Q�l���͂������ŏЉ�Ă��܂��̂ŎQ�l�ɂ��Ă݂Ă��������B
�X�|���T�[�����N
�d���O��u���_�v����21�N�x ��6�̉ߋ���Ɖ���@�֘A�y�[�W
- �d���O��u���_�v����21�N�x ��1�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��1�̉ߋ���Ɖ���ł��B���̉ߋ���͓d���A�d�E�A�R���f���T�Ɋւ����{�I�Ȍ�����������Ή�������ł��B
- �d���O��u���_�v����21�N�x ��2�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��2�̉ߋ���Ɖ���ł��B���̉ߋ���͐Ód�E�Ɋւ����{�I�Ȓm���̐����₤���ł��B
- �d���O��u���_�v����21�N�x ��3�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��3�̉ߋ���Ɖ���ł��B���̉ߋ���̓R�C���̎������𐔂ƃR�C���ɒ~�����鎥�C�G�l���M�[�Ɋւ�����ł��B
- �d���O��u���_�v����21�N�x ��4�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��4�̉ߋ���Ɖ���ł��B���̉ߋ���͐�`�����ɗ����d���ɂ�����鎥�E�Ɋւ�����ł��B�d���O��ł悭�o�肳��₷���p�^�[���̖��ł��B
- �d���O��u���_�v����21�N�x ��5�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��5�̉ߋ���Ɖ���ł��B���̉ߋ���̓R���f���T������E����ڑ��A�d��������E����ɐڑ�����Ă���Ƃ��̓d�E�̃G�l���M�[�i�Ód�G�l���M�[�j�����߂���ł��B
- �d���O��u���_�v����21�N�x ��7�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��7�̉ߋ���Ɖ���ł��B���̉ߋ���͒P��3�����𗬉�H�̌v�Z���ŁA3���ɗ����e���d���̑傫���̑召�W�����߂���ł��B�d�����Ɋe���ׂɗ����d�������߁A�L���q�z�b�t�̖@���i�d�����j��K�p���Ċe���d�������߂܂��B
- �d���O��u���_�v����21�N�x ��8�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��8�̉ߋ���Ɖ���ł��B���̉ߋ���͒P���𗬉�H�̌v�Z���ŁA�X�C�b�`S���J���Ă���Ƃ��ƕ��Ă���Ƃ��̂��ꂼ��̓d���̔�ƈʑ����̍������߂���ł��B�X�C�b�`S���J���Ă���Ƃ��ƕ��Ă���Ƃ��ŕ����Čv�Z���Ă����܂��B
- �d���O��u���_�v����21�N�x ��9�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��9�̉ߋ���Ɖ���ł��B���̉ߋ���͐����g�𗬓d���Ɋւ�����ŁA�d���̏u���l������l�ɂȂ�Ƃ��̎��������߂���ł��B�d�C�̖��ƌ��������A�قڐ��w�̖��ɋ߂��ł��B


