電験三種「理論」平成21年度問1の過去問と解説

※ページ内にPR･広告が含まれる場合があります。

電験三種「理論」平成21年度問1の過去問の解説です。

電験三種「理論」平成21年度（2009年度）　問1

電験三種「理論」の平成21年度問1（A問題）の問題です。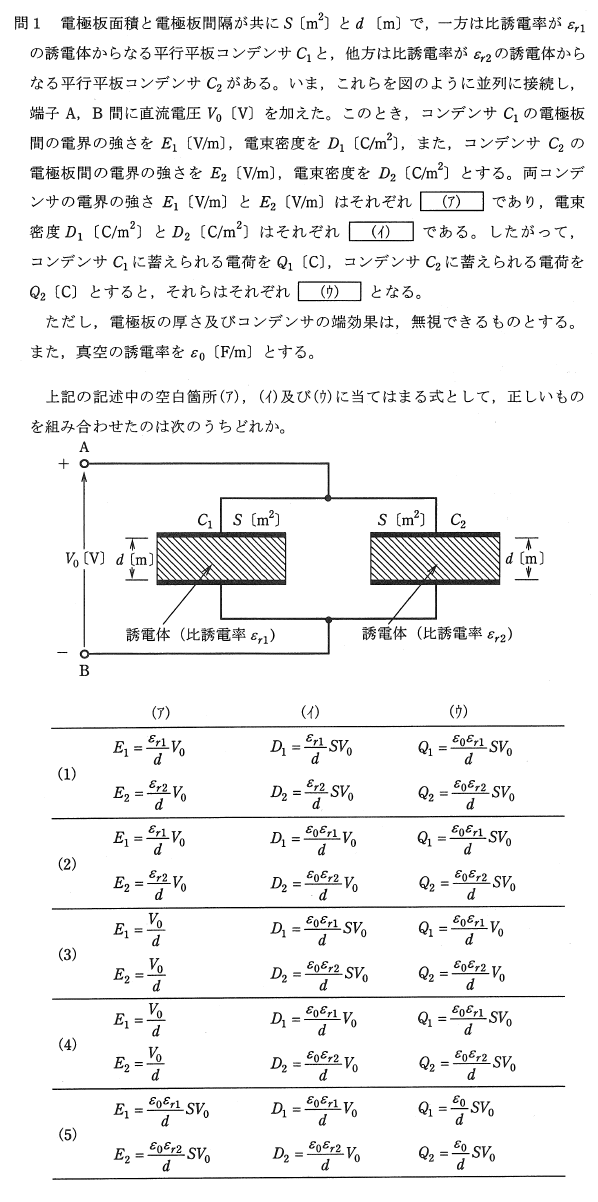
電験三種「理論」平成21年度（2009年度）問1の問題

この問題を解くためのポイント

この問題を解くためのポイントは、

コンデンサが電源に並列に接続されている。つまり、どちらのコンデンサにも同じ電源電圧がかかる。
電界の強さ、電束密度、コンデンサに関する基本的な公式を知っているか？

です。

ポイント1

ポイント1．は電気回路を考えるときのちょー基本なのですが、問題の回路図をみると抵抗ではなくコンデンサなので、たまに気付かない人もいます。（そんなことないか？）

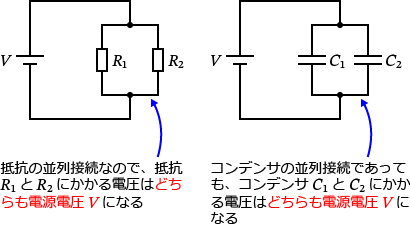
抵抗の並列回路とコンデンサの並列回路

上の左図は抵抗の並列接続回路ですが、抵抗の回路であれば「抵抗 $R_1$ と $R_2$ にかかる電圧はどちらも電源電圧 $V$ になる」というのは分かると思います。

一方、上の右図はコンデンサの並列接続回路です。コンデンサの並列接続回路でも抵抗の回路と同様に「コンデンサ $C_1$ と $C_2$ にかかる電圧はどちらも電源電圧 $V$」になります。

回路の素子（この場合、抵抗か？コンデンサか？）が違っていても素子にかかる電圧は同じということですね。

ポイント2

ポイント2．は電界の強さ、電束密度、コンデンサに関する基本的な公式を知っていればいいだけですが、電束密度の公式を忘れている人が多いです。
電束密度の公式・・・、忘れちゃったりしてないですか？

電験三種「理論」平成21年度（2009年度）　問1（A問題）の解説

（ア）電界の強さE1、E2を求める問題

（ア）は電界の強さ $E_1$、$E_2$ を求める問題で、電圧と電界の強さの関係を表わす公式が分かれば簡単に求められます。電圧と電界の強さの関係を表わす公式は、電圧を $V$、電界を $E$、コンデンサの電極板間隔を $d$ とすると、

$V=E\, d$　…①　ですね。

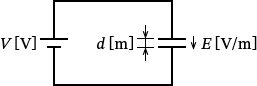
電圧と電界の関係

それで、「この問題を解くためのポイント」でも書きましたが、問題の回路図は電源にコンデンサ $C_1$ と $C_2$ が並列接続されているので、コンデンサ $C_1$ と $C_2$ にかかる電圧はどちらも電源電圧 $V_0$［$\mathrm{V}$］になります。

並列接続されたコンデンサにかかる電圧はどちらもV0［V］

それから、コンデンサの電極板間隔は、問題に書いてあるようにどちらのコンデンサも $d$［$\mathrm{m}$］ですね。

したがって、求めたい電界の強さ $E_1$ は、①の公式に電圧 $V_0$ とコンデンサの電極板間隔 $d$ をあてはめて、

$V_0=E_1\, d$

$\therefore E_1=\dfrac{V_0}{d}$　［$\mathrm{V/m}$］　…（答）

となります。

また、もう一つの求めたい電界の強さ $E_2$ も同じようにして求められ、

$V_0=E_2\, d$

$\therefore E_2=\dfrac{V_0}{d}$　［$\mathrm{V/m}$］　…（答）

となります。

（イ）電束密度D1、D2を求める問題

（イ）は電束密度 $D_1$、$D_2$ を求める問題で、電束密度と電界の強さの関係を表わす公式が分かれば求められます。

電束密度と電界の強さの関係を表わす公式は、電束密度を $D$、電界の強さを $E$、コンデンサの誘電体の誘電率を $\varepsilon$ とすると、

$D=\varepsilon\,E$　…②　です。

②の公式の電界の強さ $E$ は（ア）で求められているので、あとは誘電体の誘電率 $\varepsilon$ が分かれば電束密度 $D$ を求められます。

問題を見てみると、真空の誘電率は $\varepsilon_0$、コンデンサ $C_1$ の比誘電率は $\varepsilon_{r1}$、コンデンサ $C_2$ の比誘電率は $\varepsilon_{r2}$ と書いてあるので、コンデンサ $C_1$、$C_2$ の誘電体の誘電率をそれぞれ $\varepsilon_1$、$\varepsilon_2$ とすると、

$\varepsilon_1 =\varepsilon_0\cdot\varepsilon_{r1}$

$\varepsilon_2 =\varepsilon_0\cdot\varepsilon_{r2}$

となります。

したがって、コンデンサ $C_1$ の電束密度 $D_1$ は、

$D_1=\varepsilon_1\, E_1=\varepsilon_0\,\varepsilon_{r1}\cdot\dfrac{V_0}{d} =\dfrac{\varepsilon_0\,\varepsilon_{r1}}{d} V_0$

$\therefore D_1=\dfrac{\varepsilon_0\,\varepsilon_{r1}}{d} V_0$　［$\mathrm{C/m^2}$］　…（答）

となり、コンデンサ $C_2$ の電束密度 $D_2$ は、

$D_2=\varepsilon_2\, E_2=\varepsilon_0\,\varepsilon_{r2}\cdot\dfrac{V_0}{d} =\dfrac{\varepsilon_0\,\varepsilon_{r2}}{d} V_0$

$\therefore D_2=\dfrac{\varepsilon_0\,\varepsilon_{r2}}{d} V_0$　［$\mathrm{C/m^2}$］　…（答）

となります。

（ウ）コンデンサに蓄えられる電荷Q1、Q2を求める問題

（ウ）はコンデンサに蓄えられる電荷 $Q_1$、$Q_2$ を求める問題で、コンデンサに蓄えられる電荷と電圧の関係を表わす公式を使って求めていきます。

コンデンサに蓄えられる電荷と電圧の関係を表わす公式は、蓄えられる電荷を $Q$、コンデンサにかかる電圧を $V$、コンデンサの静電容量を $C$ とすると、

$Q=C\,V$　…③　です。

③式の電圧 $V$ は（ア）でも説明したようにコンデンサ $C_1$、$C_2$ ともに $V_0$ になるので、あとはコンデンサの静電容量が分かればいいですね。

コンデンサ $C_1$ と $C_2$ の静電容量をそれぞれ ${C_1}^\prime$、${C_2}^\prime$ とすると、コンデンサの静電容量の公式より、

${C_1}^\prime =\varepsilon_0\,\varepsilon_{r1}\cdot\dfrac{S}{d}$　、　${C_2}^\prime =\varepsilon_0\,\varepsilon_{r2}\cdot\dfrac{S}{d}$

となります。（コンデンサの静電容量の公式 $\left( C=\varepsilon\dfrac{S}{d}\right)$ に、$C_1$、$C_2$ それぞれの誘電率、電極板面積、電極板間隔をあてはめただけです。）

したがって、コンデンサ $C_1$ に蓄えられる電荷 $Q_1$ は、

$Q_1={C_1}^\prime\, V_0=\varepsilon_0\,\varepsilon_{r1}\cdot\dfrac{S}{d}\cdot V_0$ $=\dfrac{\varepsilon_0\,\varepsilon_{r1}}{d} S\, V_0$

$\therefore Q_1=\dfrac{\varepsilon_0\,\varepsilon_{r1}}{d} S\, V_0$　［$\mathrm{C}$］　…（答）

となり、コンデンサ $C_2$ に蓄えられる電荷 $Q_2$ は、

$Q_2={C_2}^\prime\, V_0=\varepsilon_0\,\varepsilon_{r2}\cdot\dfrac{S}{d}\cdot V_0$ $=\dfrac{\varepsilon_0\,\varepsilon_{r2}}{d} S\, V_0$

$\therefore Q_2=\dfrac{\varepsilon_0\,\varepsilon_{r2}}{d} S\, V_0$　［$\mathrm{C}$］　…（答）

となります。

以上で、（ア）、（イ）、（ウ）の答を求めることができました。

補足①

問題で与えられる誘電率について

この問題のように誘電体の誘電率を表わす量が「比誘電率」で与えられている場合には、誘電体の誘電率は「比誘電率」に「真空の誘電率」をかけたものになります。（誘電率＝比誘電率×真空の誘電率）

補足②

電界の強さと電界（用語）について

「電界の強さ」は、単に「電界」と言ったり、「電界強度」、「電界の大きさ」と言ったりもします。

この問題を解くために使った公式

電圧と電界の強さの公式：$V=E\, d$

電束密度と電界の強さの公式：$D=\varepsilon\, E$

誘電率の公式：$\varepsilon =\varepsilon_0\,\varepsilon_r$

電荷の公式：$Q=C\, V$

コンデンサの静電容量の公式：$C=\varepsilon_0\,\varepsilon_r\dfrac{S}{d}$

この問題のように電験三種の問題では、公式を知っているか？知らないか？で得点できる、できないが決まる問題も多くあるので、過去問題を解くときに使った公式は最低限おぼえておくようにしましょう。

コンデンサの直列接続と並列接続についてもうちょっと詳しく知りたい方は、こちらのコンデンサの静電容量と電荷の計算の基本（直列接続と並列接続）のページにまとめていますので参考にしてみてください。

おすすめの電験三種の過去問題集はこちら、電験三種の参考書はこちら、電験三種用の数学参考書はこちらで紹介していますので参考にしてみてください。

このページに掲載の問題は、（一財）電気技術者試験センターが作成した第三種電気主任技術者試験（電験三種）の問題です。

電験（電気主任技術者試験）のＴＯＰ　←BACK

NEXT→　電験三種「理論」平成21年度　問2の過去問と解説

電験三種「理論」平成21年度問1の過去問と解説　関連ページ

電験三種「理論」平成21年度問2の過去問と解説: 電験三種「理論」平成21年度（2009年度）問2の過去問と解説です。この過去問は静電界に関する基本的な知識の正誤を問う問題です。
電験三種「理論」平成21年度問3の過去問と解説: 電験三種「理論」平成21年度（2009年度）問3の過去問と解説です。この過去問はコイルの磁束鎖交数とコイルに蓄えられる磁気エネルギーに関する問題です。
電験三種「理論」平成21年度問4の過去問と解説: 電験三種「理論」平成21年度（2009年度）問4の過去問と解説です。この過去問は扇形導線に流れる電流により作られる磁界に関する問題です。電験三種でよく出題されやすいパターンの問題です。
電験三種「理論」平成21年度問5の過去問と解説: 電験三種「理論」平成21年度（2009年度）問5の過去問と解説です。この過去問はコンデンサが直列・並列接続、電源が直列・並列に接続されているときの電界のエネルギー（静電エネルギー）を求める問題です。
電験三種「理論」平成21年度問6の過去問と解説: 電験三種「理論」平成21年度（2009年度）問6の過去問と解説です。この過去問は抵抗が直列接続、並列接続された直流回路の基本的な問題で、与えられた電圧・電流の回路条件から抵抗値を求める問題です。ここではキルヒホッフの法則を使って解いています。
電験三種「理論」平成21年度問7の過去問と解説: 電験三種「理論」平成21年度（2009年度）問7の過去問と解説です。この過去問は単相3線式交流回路の計算問題で、3線に流れる各線電流の大きさの大小関係を求める問題です。電源毎に各負荷に流れる電流を求め、キルヒホッフの法則（電流則）を適用して各線電流を求めます。
電験三種「理論」平成21年度問8の過去問と解説: 電験三種「理論」平成21年度（2009年度）問8の過去問と解説です。この過去問は単相交流回路の計算問題で、スイッチSが開いているときと閉じているときのそれぞれの電流の比と位相差の差を求める問題です。スイッチSが開いているときと閉じているときで分けて計算していきます。
電験三種「理論」平成21年度問9の過去問と解説: 電験三種「理論」平成21年度（2009年度）問9の過去問と解説です。この過去問は正弦波交流電流に関する問題で、電流の瞬時値がある値になるときの時刻を求める問題です。電気の問題と言うよりも、ほぼ数学の問題に近いです。

電験三種｜理論｜平成21年度問1の過去問と解説