�X�|���T�[�����N
�d���O��u���_�v����21�N�x ��8�̉ߋ���Ɖ��
���y�[�W����PR��L�����܂܂��ꍇ������܂��B
�d���O��u���_�v����21�N�x��8�̉ߋ���̉���ł��B
�d���O��u���_�v����21�N�x�i2009�N�x�j�@��8
�d���O��u���_�v�̕���21�N�x��8�iA���j�̖��ł��B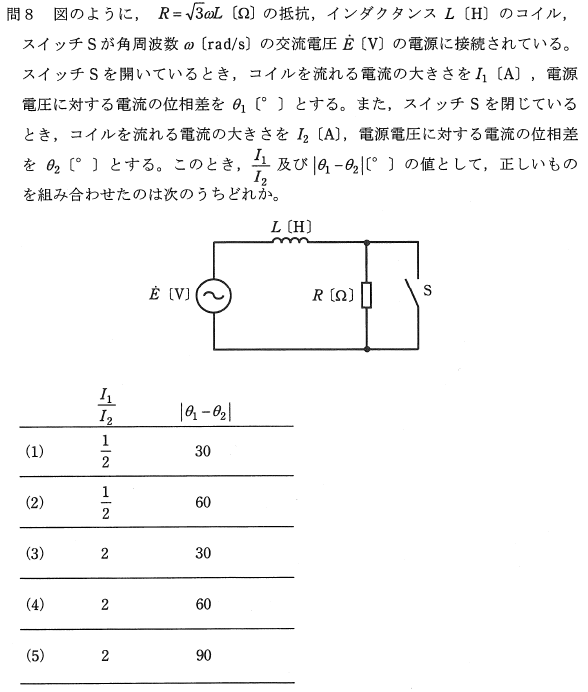
���̖����������߂̃|�C���g�ƃR�c
���̖����������߂̃|�C���g�ƃR�c�́A
- �X�C�b�` $\mathrm{S}$ ���J���Ă���Ƃ��ƕ��Ă���Ƃ��ŕ����čl���悤�I
- �P���𗬉�H�̌v�Z���@�͕�����܂����H
- ��R���Z�������ƒ�R�ɂ͓d��������Ȃ��I�i��R�͖����̂Ɠ����j
- �d���̔�����߂�Ƃ��͕���ƕ��q���ԈႦ�Ȃ��悤�ɂ��悤�I
�ł��B
�X�|���T�[�����N
�X�|���T�[�����N
�d���O��u���_�v����21�N�x�i2009�N�x�j�@��8�iA���j�̉��
���̉ߋ���͒P���𗬉�H�̖��ŁA�X�C�b�` $\mathrm{S}$ ���J���Ă���Ƃ��ƕ��Ă���Ƃ��̂��ꂼ��̓d���̔�ƈʑ����̍������߂���ł��B
�ł́A�X�C�b�` $\mathrm{S}$ ���J���Ă���Ƃ�����v�Z���Ă����܂��傤�B
�X�C�b�`S���J���Ă���Ƃ�
�X�C�b�` $\mathrm{S}$ ���J���Ă���Ƃ��̉�H�}�́A���̂悤�ɂȂ�܂��ˁB�i���āA���̉�H�}���̂܂�܂ł��B�j
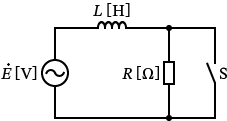
�X�C�b�` $\mathrm{S}$ ���J���Ă���̂ŁA���̉�H�͎��̂悤��RL�����H�Ƃ������ƂɂȂ�܂��B
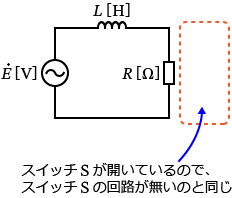
����Ŗ�蕶������ƁA�u�R�C���𗬂��d���̑傫���� $I_1$�v�Ə����Ă���̂ŁA$I_1$ �͂܂�A��H�S�̂ɗ����d���ɂȂ�܂��B
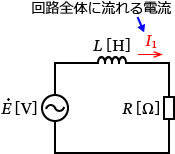
�Ȃ̂ŁA�d�� $I_1$ �����߂邽�߂ɂ́A��H�̍����C���s�[�_���X $\dot{Z_1}$ �����߂āA�I�[���̖@�����g�������ł��ˁB
���̉�H��RL�����H�œd���̊p���g���� $\omega$ �Ȃ̂ŁA��H�̍����C���s�[�_���X $\dot{Z_1}$ �́A
$\dot{Z_1} =R+j\omega L=\sqrt{3}\,\omega L+j\omega L$�@�i$\because R=\sqrt{3}\,\omega L$�j
$\therefore \dot{Z_1} =\sqrt{3}\,\omega L+j\omega L$�@�m$\Omega$�n�@�ƂȂ�܂��B
���Ƃ̓I�[���̖@�����g���ēd�� $\dot{I_1}$ ���v�Z����ƁA
$\dot{I_1} =\dfrac{\dot{E}}{\dot{Z_1}} =\dfrac{\dot{E}}{\sqrt{3}\,\omega L+j\omega L}$ $=\dfrac{1}{\omega L}\left(\dfrac{1}{\sqrt{3} +j}\right)\dot{E}$ $=\dfrac{1}{\omega L}\left\{\dfrac{\sqrt{3} -j}{\left(\sqrt{3} +j\right)\left(\sqrt{3} -j\right)}\right\}\dot{E}$
$=\dfrac{1}{\omega L}\left(\dfrac{\sqrt{3} -j}{3+1}\right)\dot{E}$ $=\left(\dfrac{\sqrt{3} -j}{4\,\omega L}\right)\dot{E}$ $=\left(\dfrac{\sqrt{3}}{4\,\omega L} -j\dfrac{1}{4\,\omega L}\right)\dot{E}$
$\therefore \dot{I_1} =\left(\dfrac{\sqrt{3}}{4\,\omega L} -j\dfrac{1}{4\,\omega L}\right)\dot{E}$�@�m$\mathrm{A}$�n�@�c�@�@�ƂȂ�܂��B
�d�� $\dot{I_1}$ �̎������߂�ꂽ�̂ŁA�d���d�� $\dot{E}$ �̑傫���� $E$ �Ƃ��ēd�� $\dot{I_1}$ �̑傫�� $I_1$ �����߂܂��B
$I_1=|\dot{I_1} |$ $=\sqrt{\left(\dfrac{\sqrt{3}}{4\,\omega L}\right)^2 +\left(\dfrac{1}{4\,\omega L}\right)^2}\cdot E$ $=\sqrt{\dfrac{3+1}{\left( 4\,\omega L\right)^2}}\cdot E$ $=\sqrt{\dfrac{4}{\left( 4\omega L\right)^2}}\cdot E$ $=\dfrac{2E}{4\,\omega L}$ $=\dfrac{E}{2\,\omega L}$
$\therefore I_1=\dfrac{E}{2\,\omega L}$�@�m$\mathrm{A}$�n�@�c�A
���́A�@�����d���d�� $\dot{E}$ �ɑ���d�� $\dot{I_1}$ �̈ʑ��� $\theta_1$ �� $\tan$ ���g���ċ��߂܂��B�i�d���̔� $\dfrac{I_1}{I_2}$ �ɂ��ẮA�d�� $I_2$ �̎����v�Z���Ă��狁�߂܂��B�j
$\tan\theta_1 =\dfrac{-\dfrac{1}{4\,\omega L}}{\dfrac{\sqrt{3}}{4\,\omega L}} =\dfrac{-1}{\sqrt{3}}$
$\theta_1 =\tan^{-1}\left(\dfrac{-1}{\sqrt{3}}\right) =-30^\circ$
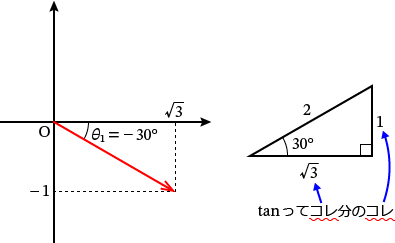
$\therefore \theta_1 =-30^\circ$�@�c�B�@�ƂȂ�܂��B
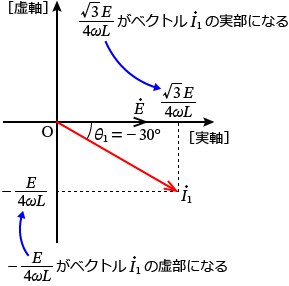
���Ȃ݂ɁA�@���̓d���d�� $\dot{E}$ �Ɠd�� $\dot{I_1}$ �̃x�N�g���}���A�d�� $\dot{E}$ ����ɂ��ď����Ǝ��̂悤�ɂȂ�܂��B�i$E$ �̓x�N�g�� $\dot{E}$ �̑傫����\�킵�܂��B�j
�X�C�b�`S�����Ă���Ƃ�
�X�C�b�` $\mathrm{S}$ �����Ă���Ƃ��̉�H�}�́A���̂悤�ɂȂ�܂��ˁB
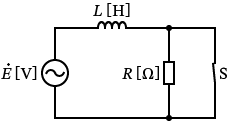
�X�C�b�` $\mathrm{S}$ �����Ă���̂ŁA��R $R$ �͒Z������Ă��邱�ƂɂȂ�܂��B�Ȃ̂ŁA��R $R$ �ɂ͓d��������Ȃ��̂ŁA���̉�H�͎��̂悤�ɃR�C�� $L$ �����̉�H�ɂȂ�܂��B
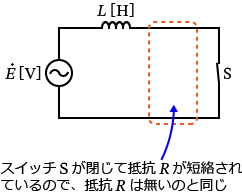
�ł́A�d�� $\dot{I_1}$ �Ɠ����悤�ɁA�I�[���̖@�����g���ēd�� $\dot{I_2}$ ���v�Z���Ă݂܂��傤�B
$\dot{I_2} =\dfrac{\dot{E}}{j\omega L} =\dfrac{1}{j\omega L}\dot{E} =\dfrac{j}{j\times j\omega L}\dot{E}$ $=-j\dfrac{1}{\omega L}\dot{E}$
$\therefore \dot{I_2} =-j\dfrac{1}{\omega L}\dot{E}$�@�m$\mathrm{A}$�n�@�c�C�@�ƂȂ�܂��B
�d�� $\dot{I_2}$ �̎������߂�ꂽ�̂ŁA�d���d�� $\dot{E}$ �̑傫���� $E$ �Ƃ��ēd�� $\dot{I_2}$ �̑傫�� $I_2$ �����߂܂��B
$I_2=|\dot{I_2} |=\sqrt{0^2+\left(\dfrac{1}{\omega L}\right)^2}\cdot E$ $=\sqrt{\dfrac{1}{\left(\omega L\right)^2}}\cdot E$ $=\dfrac{E}{\omega L}$
$\therefore I_2=\dfrac{E}{\omega L}$�@�m$\mathrm{A}$�n�@�c�D
���́A�C�����d���d�� $\dot{E}$ �ɑ���d�� $\dot{I_2}$ �̈ʑ��� $\theta_2$ �� $\tan$ ���g���ċ��߂܂��B
$\tan\theta_2 =\dfrac{-\dfrac{E}{\omega L}}{0} =-\infty$�@�i$\because$�[�����̂Ȃ�Ƃ��i�Ȃ�Ƃ����[���j�͖�����ɂȂ�܂��B�j
$\theta_2 =\tan^{-1}\left( -\infty\right) =-90^\circ$
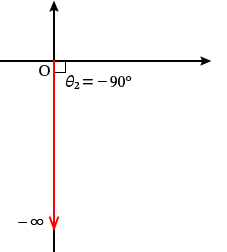
$\therefore \theta_2 =-90^\circ$�@�c�E�@�ƂȂ�܂��B
���Ȃ݂ɁA�C���̓d���d�� $\dot{E}$ �Ɠd�� $\dot{I_2}$ �̃x�N�g���}���A�d�� $\dot{E}$ ����ɂ��ď����Ǝ��̂悤�ɂȂ�܂��B
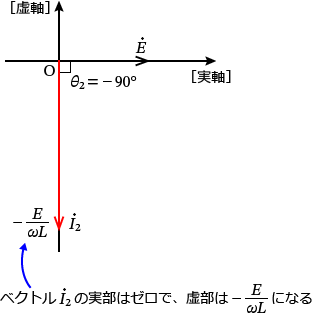
�ȏ�œd�� $I_1$ �� $I_2$ �̑傫���ƁA�ʑ��� $\theta_1$ �� $\theta_2$ �����߂�ꂽ�̂ŁA�Ō�ɓd���̔� $\dfrac{I_1}{I_2}$ �ƈʑ����̍� $|\theta_1 -\theta_2 |$ �����߂�ΏI���ł��B
�A�A�D���d���̔� $\dfrac{I_1}{I_2}$ �́A
$\dfrac{I_1}{I_2} =\dfrac{\dfrac{E}{2\,\omega L}}{\dfrac{E}{\omega L}} =\dfrac{1}{2}$
$\therefore \dfrac{I_1}{I_2} =\dfrac{1}{2}$�@�c�i���j
�B�A�E���ʑ����̍� $|\theta_1 -\theta_2 |$ �́A
$|\theta_1 -\theta_2 | =|-30^\circ -\left( -90^\circ\right) |$ $=|-30^\circ +90^\circ |$ $=|60^\circ |$ $=60^\circ$
$\therefore |\theta_1 -\theta_2 |=60^\circ$�@�c�i���j
�ƂȂ�A�i2�j�������ɂȂ�܂��B
���̖����������߂Ɏg��������
�I�[���̖@���̌����F$\dot{I} =\dfrac{\dot{E}}{\dot{Z}}$
RL�����H�̃C���s�[�_���X�̌����F$\dot{Z} =R+j\omega L$
�O�p���̌����i$\tan$�j�F$\tan\theta =\dfrac{b}{a}$
�p�x�����߂�����i$\tan$�j�F$\theta =\tan^{-1}\dfrac{b}{a}$
�x�N�g���̑傫���̌����F$|\dot{r} |=\sqrt{a^2+b^2}$
�𗬉�H�̌v�Z�ł͋����P�ʁu$j$�v���悭�g���܂����A���̋����P�ʁu$j$�v�����Ƃ������͂����������܂��B
�d���O��̖��ł́A�u�����P�ʁu$j$�v���悷��Ɓu-1�v�ɂȂ�v�Ƃ�����{�������ڂ��Ă����قƂ�ǂ̌v�Z���͉����܂��̂ŁA���܂���ӎ��������Ȃ��悤�ɂ��܂��傤�B�����ΊȒP�ł��B
�܂��A�d���O��̖��ł́A���̖��̂悤�ɔ�����߂��肪�o�肳��邱�Ƃ�����܂��B���߂��̕���ƕ��q���ԈႤ�ƁA�Ԉ�����I������I��ł��܂����Ƃ�����̂ŋC��t���܂��傤�I
���Ȃ݂ɂ��̖��̏ꍇ�A$I_1$ �� $I_2$ �� $\dfrac{I_2}{I_1}$ �Ƌ��߂Ă��܂��ƑI�����́i4�j��I��ł��܂��s�����ɂȂ��Ă��܂��܂���B
�X�|���T�[�����N
�X�|���T�[�����N
�������߂��d���O��̉ߋ����W�͂������A�d���O��̎Q�l���͂������A�d���O��p�̐��w�Q�l���͂������ŏЉ�Ă��܂��̂ŎQ�l�ɂ��Ă݂Ă��������B
�X�|���T�[�����N
�d���O��u���_�v����21�N�x ��8�̉ߋ���Ɖ���@�֘A�y�[�W
- �d���O��u���_�v����21�N�x ��1�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��1�̉ߋ���Ɖ���ł��B���̉ߋ���͓d���A�d�E�A�R���f���T�Ɋւ����{�I�Ȍ�����������Ή�������ł��B
- �d���O��u���_�v����21�N�x ��2�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��2�̉ߋ���Ɖ���ł��B���̉ߋ���͐Ód�E�Ɋւ����{�I�Ȓm���̐����₤���ł��B
- �d���O��u���_�v����21�N�x ��3�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��3�̉ߋ���Ɖ���ł��B���̉ߋ���̓R�C���̎������𐔂ƃR�C���ɒ~�����鎥�C�G�l���M�[�Ɋւ�����ł��B
- �d���O��u���_�v����21�N�x ��4�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��4�̉ߋ���Ɖ���ł��B���̉ߋ���͐�`�����ɗ����d���ɂ�����鎥�E�Ɋւ�����ł��B�d���O��ł悭�o�肳��₷���p�^�[���̖��ł��B
- �d���O��u���_�v����21�N�x ��5�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��5�̉ߋ���Ɖ���ł��B���̉ߋ���̓R���f���T������E����ڑ��A�d��������E����ɐڑ�����Ă���Ƃ��̓d�E�̃G�l���M�[�i�Ód�G�l���M�[�j�����߂���ł��B
- �d���O��u���_�v����21�N�x ��6�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��6�̉ߋ���Ɖ���ł��B���̉ߋ���͒�R������ڑ��A����ڑ����ꂽ������H�̊�{�I�Ȗ��ŁA�^����ꂽ�d���E�d���̉�H���������R�l�����߂���ł��B�����ł̓L���q�z�b�t�̖@�����g���ĉ����Ă��܂��B
- �d���O��u���_�v����21�N�x ��7�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��7�̉ߋ���Ɖ���ł��B���̉ߋ���͒P��3�����𗬉�H�̌v�Z���ŁA3���ɗ����e���d���̑傫���̑召�W�����߂���ł��B�d�����Ɋe���ׂɗ����d�������߁A�L���q�z�b�t�̖@���i�d�����j��K�p���Ċe���d�������߂܂��B
- �d���O��u���_�v����21�N�x ��9�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��9�̉ߋ���Ɖ���ł��B���̉ߋ���͐����g�𗬓d���Ɋւ�����ŁA�d���̏u���l������l�ɂȂ�Ƃ��̎��������߂���ł��B�d�C�̖��ƌ��������A�قڐ��w�̖��ɋ߂��ł��B


