�X�|���T�[�����N
�d���O��u���_�v����21�N�x ��7�̉ߋ���Ɖ��
���y�[�W����PR��L�����܂܂��ꍇ������܂��B
�d���O��u���_�v����21�N�x��7�̉ߋ���̉���ł��B
�d���O��u���_�v����21�N�x�i2009�N�x�j�@��7
�d���O��u���_�v�̕���21�N�x��7�iA���j�̖��ł��B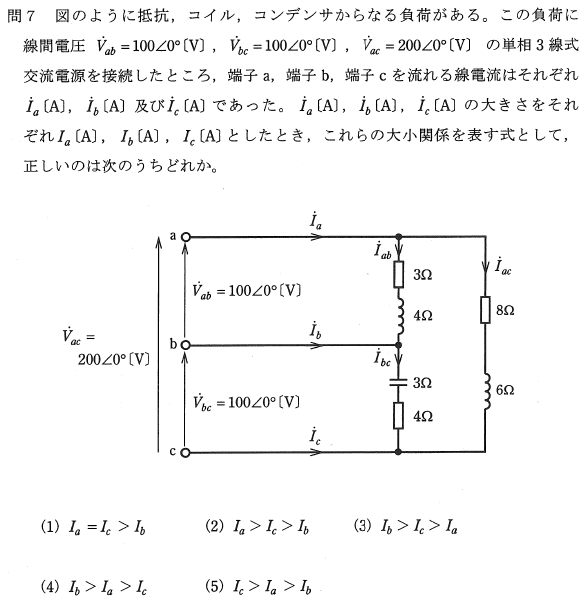
���̖����������߂̃|�C���g�ƃR�c
���̖����������߂̃|�C���g�ƃR�c�́A
- �d�����ɕ����čl���悤�I
- ���f�`���ɂ��P���𗬉�H�̌v�Z���@�͕�����܂����H
- �d�����ɕ�������H�œd�����v�Z������A�L���q�z�b�t�̖@���i�d�����j�Ŋe���d�������߂悤�I
�ł��B
�X�|���T�[�����N
�X�|���T�[�����N
�d���O��u���_�v����21�N�x�i2009�N�x�j�@��7�iA���j�̉��
���̉ߋ���͒P��3�����𗬉�H�Ɋւ���v�Z���ŁA3���ɗ����e���d�������߂���ł��B
���߂�̂�3���ɗ����e���d�� $I_a$�A$I_b$�A$I_c$ �̑召�W�ł����A���̖��͑召�W���l���Ă��������A�f���Ɋe���d�� $I_a$�A$I_b$�A$I_c$ ���v�Z���Ă��܂������������ł��B
�d���O��̗��_�̎����͂Ƃɂ������Ԃ�����Ȃ��̂ł����A�������ɂ��ꂱ��l����������ʂɌv�Z���Ă��܂����������ʓI�ɑ���������ꍇ���悭����܂��B
�ł́A�������̉���ł��B
���ƁA���̑O�ɁA���̖��̓d���ɂ��ĊȒP�ɐ������܂��B
���̖��̉�H�͒P��3�����ŁA�d���d���͂��ꂼ��A
$\dot{V_{ab}} =100\angle 0^\circ$�@�m$\mathrm{V}$�n
$\dot{V_{bc}} =100\angle 0^\circ$�@�m$\mathrm{V}$�n
$\dot{V_{ac}} =200\angle 0^\circ$�@�m$\mathrm{V}$�n
�ł��ˁB�����̓d���d���͂ǂ������d����\�킵�Ă��邩������܂����H
�Ⴆ�� $\dot{V_{ab}}$ �̏ꍇ�A
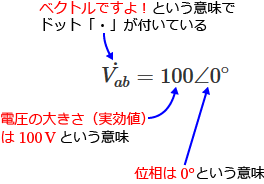
�Ƃ����Ӗ��ɂȂ�܂��B
�Ȃ̂ŁA���ꂼ��̓d���̓d������̃O���t��ɏ����Ǝ��̂悤�ɂȂ�܂��B
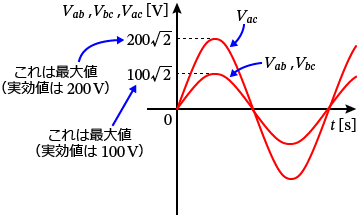
�ǂ̓d���d�����ʑ��� $0^\circ$ �ŁA$\dot{V_{ab}}$ �� $\dot{V_{bc}}$ �̎����l�� $100\,\mathrm{V}$�A$\dot{V_{ac}}$ �̎����l�� $200\,\mathrm{V}$ �Ȃ̂ŁA���̂悤�ȓd���g�`�i�O���t�j�ɂȂ�܂��B
�d���ɂ��Ă͕��������Ǝv���̂ŁA����ł͖{��́u3���ɗ����e���d���v�����߂Ă݂܂��傤�B
�e���d�������߂邽�߂ɂ͊e�d���ɂ��e���ׂɗ����d�� $\dot{I_{ab}}$�A$\dot{I_{bc}}$�A$\dot{I_{ac}}$ �����߂�K�v������A�e���ׂɗ����d�������߂�Ƃ��ɂ͊e���ׂ̕������ɍl���Ă��������ł��B�܂�A
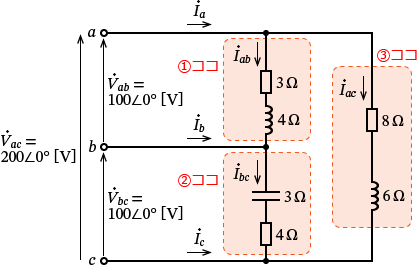
�ƁA�@�A�A�A�B��3�ӏ��ɕ����Ă��ꂼ��v�Z���Ă����܂��B
�ł́A�@�̕����ɗ����d�� $\dot{I_{ab}}$ ���珇�ԂɌv�Z���Ă݂܂��傤�I
�@�̕����ɗ����d��Iab�̌v�Z
�@�̕��������l����ƁA���̂悤�ȉ�H�ɂȂ�܂��B
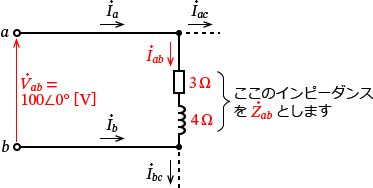
���̉�H�́A�C���s�[�_���X $\dot{Z_{ab}} =3+j\,4$ �� $\dot{V_{ab}} =100\angle 0^\circ$ �̓d�����������Ă��āA$\dot{V_{ab}}$ �ɂ��$\dot{Z_{ab}}$ �ɗ����d���� $\dot{I_{ab}}$ �ł��B�Ƃ����Ӗ��ł��ˁB
�Ȃ̂ŁA���̉�H�ɃI�[���̖@����K�p����ƁA�d�� $\dot{I_{ab}}$ �͎��̂悤�ɂȂ�܂��B
$\dot{I_{ab}} =\dfrac{\dot{V_{ab}}}{\dot{Z_{ab}}} =\dfrac{100}{3+j\,4}$�@�i$\because \dot{V_{ab}}$ �̈ʑ��� $0^\circ$ �Ȃ̂ŁA$\dot{V_{ab}} =100$ �ƂȂ�܂��B�j
$\therefore \dot{I_{ab}} =\dfrac{100}{3+j\,4}$�@�m$\mathrm{A}$�n�@�c�C
$\dot{I_{ab}}$ �����߂�ꂽ�̂ŁA���͇A�̕����ɗ����d�� $\dot{I_{bc}}$ ���v�Z���܂��B
�A�̕����ɗ����d��Ibc�̌v�Z
�A�̕��������l����ƁA���̂悤�ȉ�H�ɂȂ�܂��B
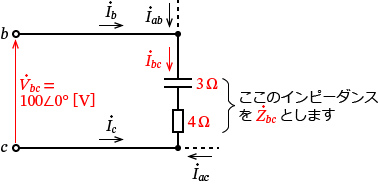
���̉�H�́A�C���s�[�_���X $\dot{Z_{bc}} =4-j\,3$ �� $\dot{V_{bc}} =100\angle 0^\circ$ �̓d�����������Ă��āA$\dot{V_{bc}}$ �ɂ��$\dot{Z_{bc}}$ �ɗ����d���� $\dot{I_{bc}}$ �ł��B�Ƃ����Ӗ��ł��ˁB
�Ȃ̂ŁA���̉�H�ɃI�[���̖@����K�p����ƁA�d�� $\dot{I_{bc}}$ �͎��̂悤�ɂȂ�܂��B
$\dot{I_{bc}} =\dfrac{\dot{V_{bc}}}{\dot{Z_{bc}}} =\dfrac{100}{4-j\,3}$�@�i$\because \dot{V_{bc}}$ �̈ʑ��� $0^\circ$ �Ȃ̂ŁA$\dot{V_{bc}} =100$ �ƂȂ�܂��B�j
$\therefore \dot{I_{bc}} =\dfrac{100}{4-j\,3}$�@�m$\mathrm{A}$�n�@�c�D
$\dot{I_{bc}}$ �����߂�ꂽ�̂ŁA���͇B�̕����ɗ����d�� $\dot{I_{ac}}$ ���v�Z���܂��B
�B�̕����ɗ����d��Iac�̌v�Z
�B�̕��������l����ƁA���̂悤�ȉ�H�ɂȂ�܂��B
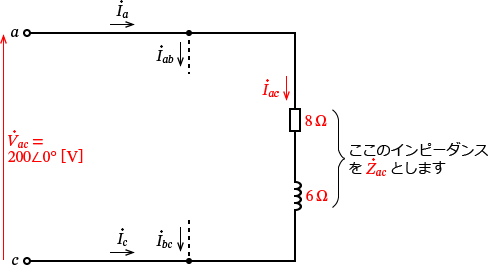
���̉�H�́A�C���s�[�_���X $\dot{Z_{ac}} =8+j\,6$ �� $\dot{V_{ac}} =200\angle 0^\circ$ �̓d�����������Ă��āA$\dot{V_{ac}}$ �ɂ��$\dot{Z_{ac}}$ �ɗ����d���� $\dot{I_{ac}}$ �ł��B�Ƃ����Ӗ��ł��ˁB
�Ȃ̂ŁA���̉�H�ɃI�[���̖@����K�p����ƁA�d�� $\dot{I_{ac}}$ �͎��̂悤�ɂȂ�܂��B
$\dot{I_{ac}} =\dfrac{\dot{V_{ac}}}{\dot{Z_{ac}}} =\dfrac{200}{8+j\,6}$�@�i$\because \dot{V_{ac}}$ �̈ʑ��� $0^\circ$ �Ȃ̂ŁA$\dot{V_{ac}} =200$ �ƂȂ�܂��B�j
$\therefore \dot{I_{ac}} =\dfrac{200}{8+j\,6}$�@�m$\mathrm{A}$�n�@�c�E
�ȏ�C�`�E���e���ׂɗ����d�������߂�ꂽ�̂ŁA���ɁA�C�`�E�ƃL���q�z�b�t�̖@���i�d�����j���g���āA3���ɗ����e���d���̑傫�� $I_a$�A$I_b$�A$I_c$ �����߂܂��B
���d��Ia�̑傫���̌v�Z
���d�� $\dot{I_a}$ �����ꍞ�ގ��̐}�̐Ԋۂ̐ڑ��_�ɒ��ڂ��܂��傤�B
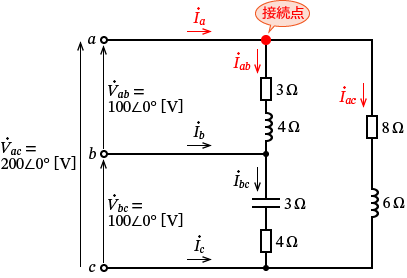
���̐Ԋۂ̐ڑ��_�ɂ͓d�� $\dot{I_a}$ �����ꍞ��ŁA�ڑ��_����d�� $\dot{I_{ab}}$ �� $\dot{I_{ac}}$ ���o�Ă����܂��B
�Ȃ̂ŁA���̐Ԋۂ̐ڑ��_�ɃL���q�z�b�t�̖@���i�d�����j��K�p����ƁA
$\dot{I_a} =\dot{I_{ab}} +\dot{I_{ac}}$�@�c�F�@�����藧���܂��B
�F���ɐ�قNj��߂��C�ƇE�������܂��B����ƁA
$\dot{I_a} =\dot{I_{ab}} +\dot{I_{ac}} =\dfrac{100}{3+j\,4} +\dfrac{200}{8+j\,6}$ $=\dfrac{100\left( 8+j\,6\right) +200\left( 3+j\,4\right)}{\left( 3+j\,4\right)\left( 8+j\,6\right)}$
$=\dfrac{800+j\,600+600+j\,800}{24+j\,18+j\,32-24}$ $=\dfrac{1400+j\,1400}{j\,50}$ $=\dfrac{28+j\,28}{j}$
$=\dfrac{j\,28+j\times j\,28}{j\times j} =\dfrac{j\,28-28}{-1}$ $=28-j\,28$
$\therefore \dot{I_a} =28-j\,28$�@�m$\mathrm{A}$�n�@�c�G
�G�̐�Βl���v�Z���đ傫�������߂܂��傤�B
$|\dot{I_a} |=I_a=\sqrt{28^2+28^2} =\sqrt{2\times 28^2}$ $=28\sqrt{2}$
$\therefore I_a=28\sqrt{2}$�@�m$\mathrm{A}$�n�@�c�H
����Ő��d�� $\dot{I_a}$ �̑傫�� $I_a$ �����߂��܂����B���́A���d�� $I_b$ �̌v�Z�ł��B
���d��Ib�̑傫���̌v�Z
���d�� $\dot{I_b}$ �����ꍞ�ގ��̐}�̐Ԋۂ̐ڑ��_�ɒ��ڂ��܂��傤�B
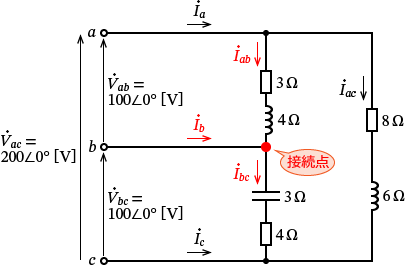
���̐Ԋۂ̐ڑ��_�ɂ͓d�� $\dot{I_b}$ �� $\dot{I_{ab}}$ �����ꍞ��ŁA�ڑ��_����d�� $\dot{I_{bc}}$ ���o�Ă����܂��B
�Ȃ̂ŁA���̐Ԋۂ̐ڑ��_�ɃL���q�z�b�t�̖@���i�d�����j��K�p����ƁA
$\dot{I_b} +\dot{I_{ab}} =\dot{I_{bc}}$�@�A�@$\dot{I_b} =\dot{I_{bc}} -\dot{I_{ab}}$�@�c�I�@�����藧���܂��B
�I���ɐ�قNj��߂��C�ƇD�������܂��B����ƁA
$\dot{I_b} =\dot{I_{bc}} -\dot{I_{ab}} =\dfrac{100}{4-j\,3} -\dfrac{100}{3+j\,4}$ $=\dfrac{100\left( 3+j\,4 \right) -100\left( 4-j\,3 \right)}{\left( 4-j\,3 \right)\left( 3+j\, 4\right)}$
$=\dfrac{300+j\,400-400+j\,300}{12+j\,16-j\,9+12}$ $=\dfrac{-100+j\,700}{24+j\,7}$ $=\dfrac{\left( -100+j\,700 \right)\left( 24-j\,7 \right)}{\left( 24+j\,7 \right)\left( 24-j\,7 \right)}$
$=\dfrac{-2400+j\,700+j\,16800+4900}{576+49}$ $=\dfrac{2500+j\,17500}{625}$ $=\dfrac{100+j\,700}{25}$ $=4+j\,28$
$\therefore \dot{I_b} =4+j\,28$�@�m$\mathrm{A}$�n�@�c�J
�J�̐�Βl���v�Z���đ傫�������߂܂��傤�B
$|\dot{I_b} |=I_b=\sqrt{4^2+28^2} =\sqrt{16+784}$ $=\sqrt{800}$ $=10\sqrt{8}$ $=10\times 2\sqrt{2}$ $=20\sqrt{2}$
$\therefore I_b=20\sqrt{2}$�@�m$\mathrm{A}$�n�@�c�K
����Ő��d�� $\dot{I_b}$ �̑傫�� $I_b$ �����߂��܂����B���́A���d�� $I_c$ �̌v�Z�ł��B
���d��Ic�̑傫���̌v�Z
���d�� $\dot{I_c}$ �����ꍞ�ގ��̐}�̐Ԋۂ̐ڑ��_�ɒ��ڂ��܂��傤�B
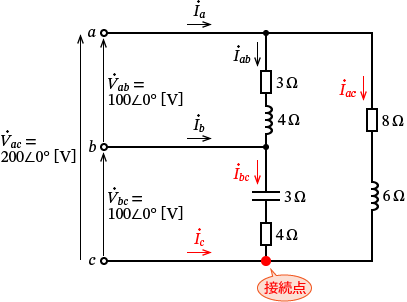
���̐Ԋۂ̐ڑ��_�ɂ͓d�� $\dot{I_c}$ �� $\dot{I_{bc}}$ �� $\dot{I_{ac}}$ �����ꍞ��ŁA�ڑ��_����o�Ă����d���͂���܂���B
�Ȃ̂ŁA���̐Ԋۂ̐ڑ��_�ɃL���q�z�b�t�̖@���i�d�����j��K�p����ƁA
$\dot{I_c} +\dot{I_{bc}} +\dot{I_{ac}} =0$�@�A�@$\dot{I_c} =-\dot{I_{bc}} -\dot{I_{ac}}$�@�c�L�@�����藧���܂��B
�L���ɐ�قNj��߂��D�ƇE�������܂��B����ƁA
$\dot{I_c} =-\dot{I_{bc}} -\dot{I_{ac}}$ $=-\dfrac{100}{4-j\,3} -\dfrac{200}{8+j\,6}$ $=-\left(\dfrac{100}{4-j\,3} +\dfrac{200}{8+j\,6}\right)$
$=-\dfrac{100\left( 8+j\,6\right) +200\left( 4-j\,3 \right)}{\left( 4-j\,3\right)\left( 8+j\,6\right)}$ $=-\dfrac{800+j\,600+800-j\,600}{32+j\,24-j\,24+18}$
$=-\dfrac{1600}{50} =-32$
$\therefore \dot{I_c} =-32$�@�m$\mathrm{A}$�n�@�c�M
���������āA$\dot{I_c}$ �̑傫�� $I_c$ �́A
$\therefore I_c=32$�@�m$\mathrm{A}$�n�@�c�N
����Ő��d�� $\dot{I_c}$ �̑傫�� $I_c$ �����߂��܂����B
�ȏ�Ŋe���d���̑傫�� $I_a$�A$I_b$�A$I_c$ �����߂�ꂽ�̂ŁA���Ƃ͂����̑召�W�����߂邾���ł��ˁB�H�A�K�A�N���A
$I_a=28\sqrt{2}\fallingdotseq 39.6$
$I_b=20\sqrt{2}\fallingdotseq 28.3$
$I_c=32.0$
�Ȃ̂ŋ��߂铚�́A�i2�j�� $I_a\gt I_c\gt I_b$�@�c�i���j�@�ɂȂ�܂��B
���̖����������߂Ɏg��������
�I�[���̖@���̌����F$\dot{I} =\dfrac{\dot{V}}{\dot{Z}}$
RL�����H�̃C���s�[�_���X�̌����F$\dot{Z} =R+jX$
RC�����H�̃C���s�[�_���X�̌����F$\dot{Z} =R-jX$
�L���q�z�b�t�̖@���i�d�����j�̌����F$\dot{I} =\dot{I_1} +\dot{I_2}$
�x�N�g���̑傫���̌����F$|\dot{r} |=\sqrt{a^2+b^2}$
�𗬉�H�̌v�Z�ł͋����P�ʁu$j$�v���悭�g���܂����A���̋����P�ʁu$j$�v�����Ƃ������͂����������܂��B
�d���O��̖��ł́A�u�����P�ʁu$j$�v��2�悷��Ɓu$-1$�v�ɂȂ�v�Ƃ�����{�������ڂ��Ă����قƂ�ǂ̌v�Z���͉����܂��̂ŁA���܂���ӎ��������Ȃ��悤�ɂ��܂��傤�B�����ΊȒP�ł��B
�X�|���T�[�����N
�X�|���T�[�����N
���̖��ł��L���q�z�b�t�̖@�����g���Ă��܂����A�L���q�z�b�t�̖@���͉�H�v�Z�̊�{�Ȃ̂ŕK���g����悤�ɂ��Ă����܂��傤�B�L���q�z�b�t�̖@���ɂ��Ă悭������Ȃ������L���q�z�b�t�̖@���̃y�[�W���Q�l�ɂ��Ă݂Ă��������B
�������߂��d���O��̉ߋ����W�͂������A�d���O��̎Q�l���͂������A�d���O��p�̐��w�Q�l���͂������ŏЉ�Ă��܂��̂ŎQ�l�ɂ��Ă݂Ă��������B
�X�|���T�[�����N
�d���O��u���_�v����21�N�x ��7�̉ߋ���Ɖ���@�֘A�y�[�W
- �d���O��u���_�v����21�N�x ��1�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��1�̉ߋ���Ɖ���ł��B���̉ߋ���͓d���A�d�E�A�R���f���T�Ɋւ����{�I�Ȍ�����������Ή�������ł��B
- �d���O��u���_�v����21�N�x ��2�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��2�̉ߋ���Ɖ���ł��B���̉ߋ���͐Ód�E�Ɋւ����{�I�Ȓm���̐����₤���ł��B
- �d���O��u���_�v����21�N�x ��3�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��3�̉ߋ���Ɖ���ł��B���̉ߋ���̓R�C���̎������𐔂ƃR�C���ɒ~�����鎥�C�G�l���M�[�Ɋւ�����ł��B
- �d���O��u���_�v����21�N�x ��4�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��4�̉ߋ���Ɖ���ł��B���̉ߋ���͐�`�����ɗ����d���ɂ�����鎥�E�Ɋւ�����ł��B�d���O��ł悭�o�肳��₷���p�^�[���̖��ł��B
- �d���O��u���_�v����21�N�x ��5�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��5�̉ߋ���Ɖ���ł��B���̉ߋ���̓R���f���T������E����ڑ��A�d��������E����ɐڑ�����Ă���Ƃ��̓d�E�̃G�l���M�[�i�Ód�G�l���M�[�j�����߂���ł��B
- �d���O��u���_�v����21�N�x ��6�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��6�̉ߋ���Ɖ���ł��B���̉ߋ���͒�R������ڑ��A����ڑ����ꂽ������H�̊�{�I�Ȗ��ŁA�^����ꂽ�d���E�d���̉�H���������R�l�����߂���ł��B�����ł̓L���q�z�b�t�̖@�����g���ĉ����Ă��܂��B
- �d���O��u���_�v����21�N�x ��8�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��8�̉ߋ���Ɖ���ł��B���̉ߋ���͒P���𗬉�H�̌v�Z���ŁA�X�C�b�`S���J���Ă���Ƃ��ƕ��Ă���Ƃ��̂��ꂼ��̓d���̔�ƈʑ����̍������߂���ł��B�X�C�b�`S���J���Ă���Ƃ��ƕ��Ă���Ƃ��ŕ����Čv�Z���Ă����܂��B
- �d���O��u���_�v����21�N�x ��9�̉ߋ���Ɖ��
- �d���O��u���_�v����21�N�x�i2009�N�x�j��9�̉ߋ���Ɖ���ł��B���̉ߋ���͐����g�𗬓d���Ɋւ�����ŁA�d���̏u���l������l�ɂȂ�Ƃ��̎��������߂���ł��B�d�C�̖��ƌ��������A�قڐ��w�̖��ɋ߂��ł��B


