第二種電気工事士学科試験の4択クイズ幹線の太さを決める根拠となる電流の最小値

※ページ内にPR･広告が含まれる場合があります。

第二種電気工事士学科試験で出題されている幹線の太さを決める根拠となる電流の最小値について4択クイズ（一問一答）にしてみました。

選択肢の中から答えを選ぶと解説も表示されるようになっているので、ちょっとした練習問題としても使えるんじゃないかなと思います。

スマホでもできるので（たぶん）、休憩時間やちょっと時間があいたときなど、スキマ時間にポチポチやってみるのもいいかもです。

選択肢の中に計算式と計算結果も書いていますので、紙と鉛筆を準備してわざわざ手計算をしなくてもいいようになっています。なので、外出先などでもポチポチさくさく進められるんじゃないかと思います。

また、このページの4択クイズをやってみて、

ぜんぜん分かんない！

というときは、こちらの幹線の太さを決める根拠となる電流の最小値（電技解釈第148条）のページを一度読んでみてからやってみてください。

一度読んでからなら、そこそこいけると思います。

幹線の太さを決める根拠となる電流の最小値の4択クイズ

問題1

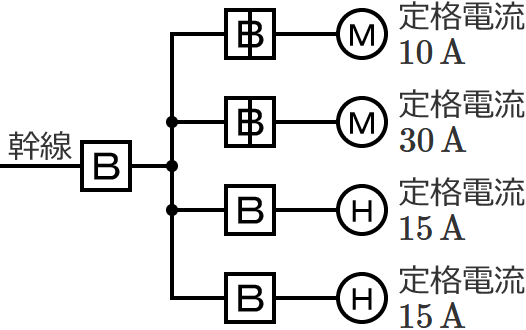
図のように、三相の電動機と電熱器が低圧屋内幹線に接続されている場合、幹線の太さを決める根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］は？　ただし、需要率は $\boldsymbol{100\,\%}$ とする。
なお、選択肢中の $\boldsymbol{I_M}$ は電動機の定格電流の合計［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_H}$ は電熱器（その他の負荷）の定格電流の合計［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_W}$ は求める幹線の太さを決める根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］です。

問題1の配線図

$\boldsymbol{I_M=10+30=40}$
$\boldsymbol{I_H=15+15=30}$
$\boldsymbol{I_W=I_M+I_H}$
$\boldsymbol{=40+30=\color{#f33}{70}}$
$\boldsymbol{I_M=10+30=40}$
$\boldsymbol{I_H=15+15=30}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 40+30=\color{#f33}{74}}$
$\boldsymbol{I_M=10+30=40}$
$\boldsymbol{I_H=15+15=30}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 40+30=\color{#f33}{80}}$
$\boldsymbol{I_M=10}$
$\boldsymbol{I_H=30+15+15=60}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 10+60=\color{#f33}{72.5}}$

正解！

はずれ！

解説

正解は、$\boldsymbol{80}$です。
幹線には定格電流 $10\,\mathrm{A}$ の電動機が $1$ 台、定格電流 $30\,\mathrm{A}$ の電動機が $1$ 台接続されているので、電動機の定格電流の合計 $I_M$ は、$I_M=10+30=\color{#f33}{40}\,\mathrm{A}$ になります。
幹線には定格電流 $15\,\mathrm{A}$ の電熱器が $2$ 台接続されているので、電熱器（その他の負荷）の定格電流の合計 $I_H$ は、$I_H=15+15=\color{#f33}{30}\,\mathrm{A}$ になります。

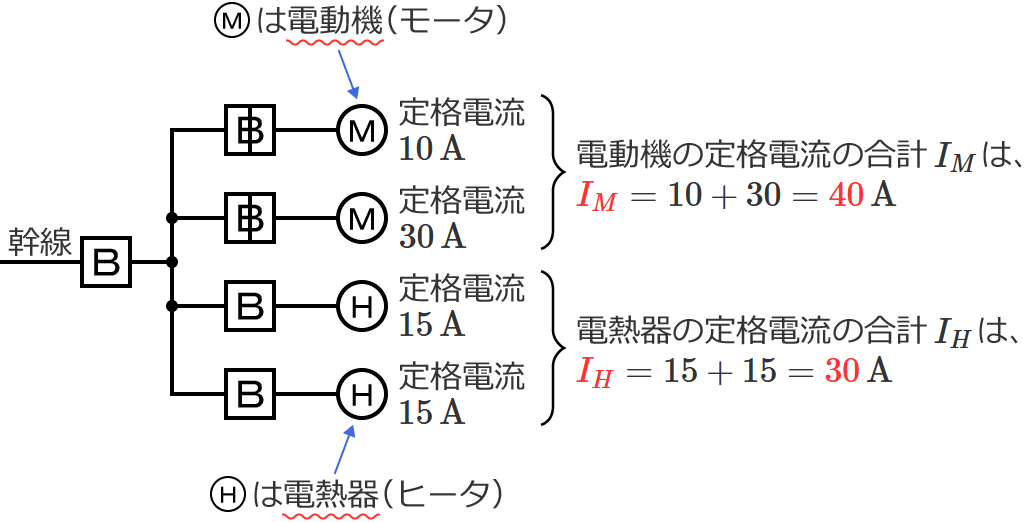
問題1の電動機と電熱器それぞれの定格電流の合計

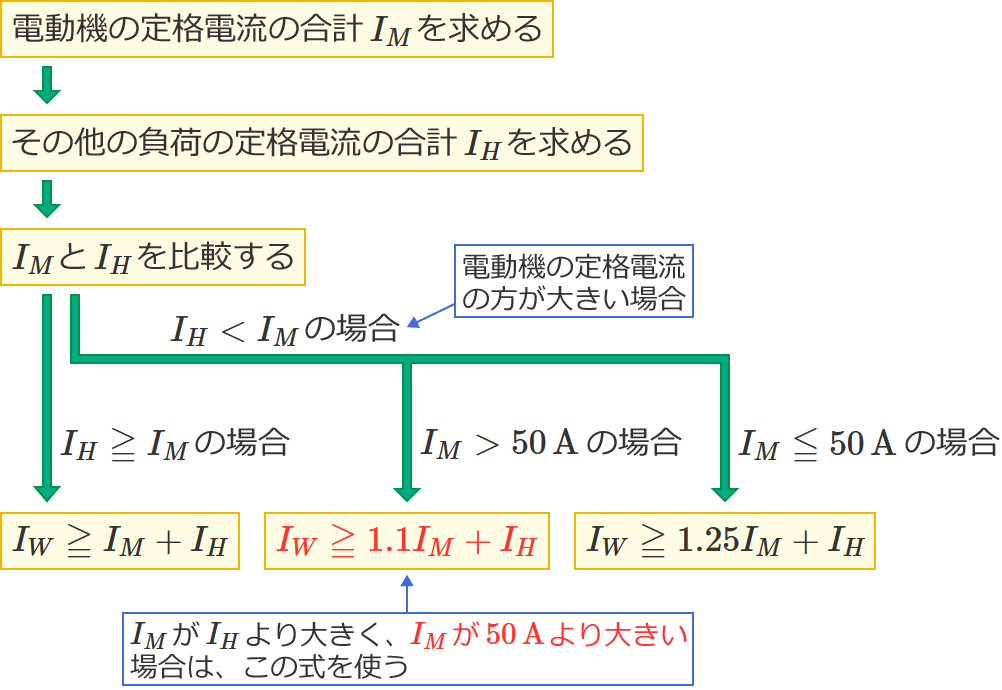
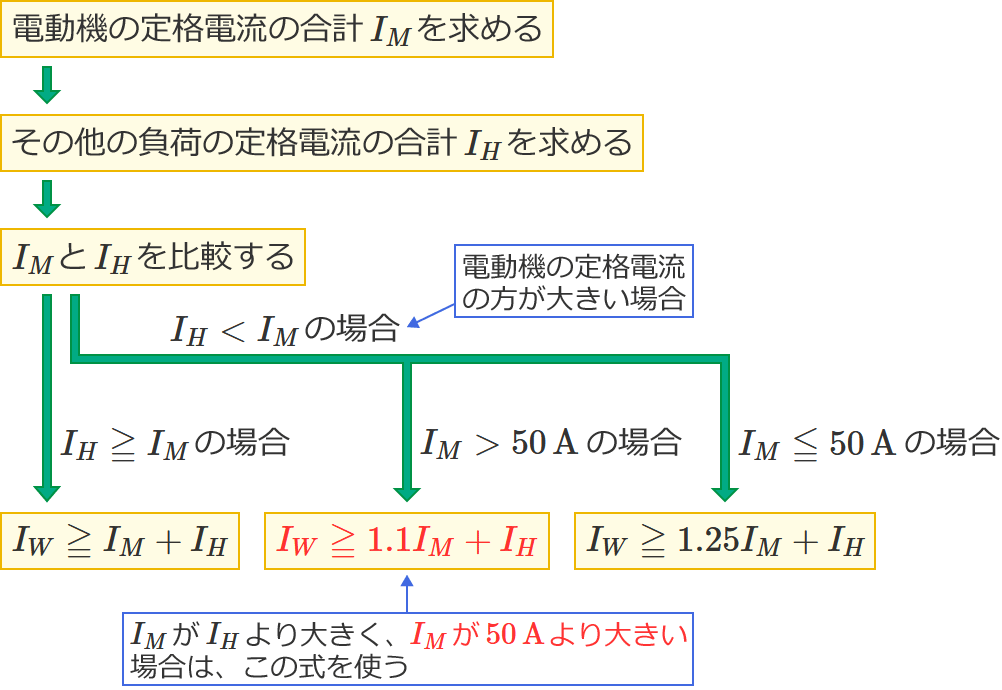
$I_M$ と $I_H$ を比較すると $I_M$ の方が大きく、$I_M$ は $50\,\mathrm{A}$ 以下なので、幹線の太さを決める根拠となる電流の最小値を求める式は $I_W=1.25I_M+I_H$ になります。
この式にぞれぞれの値を代入すると、$I_W=1.25I_M+I_H$ $=1.25\times 40+30$ $=50+30$ $=\color{#f33}{80}$ となるので、求める幹線の太さを決める根拠となる電流の最小値は $\color{#f33}{80}\,\mathrm{A}$ になります。

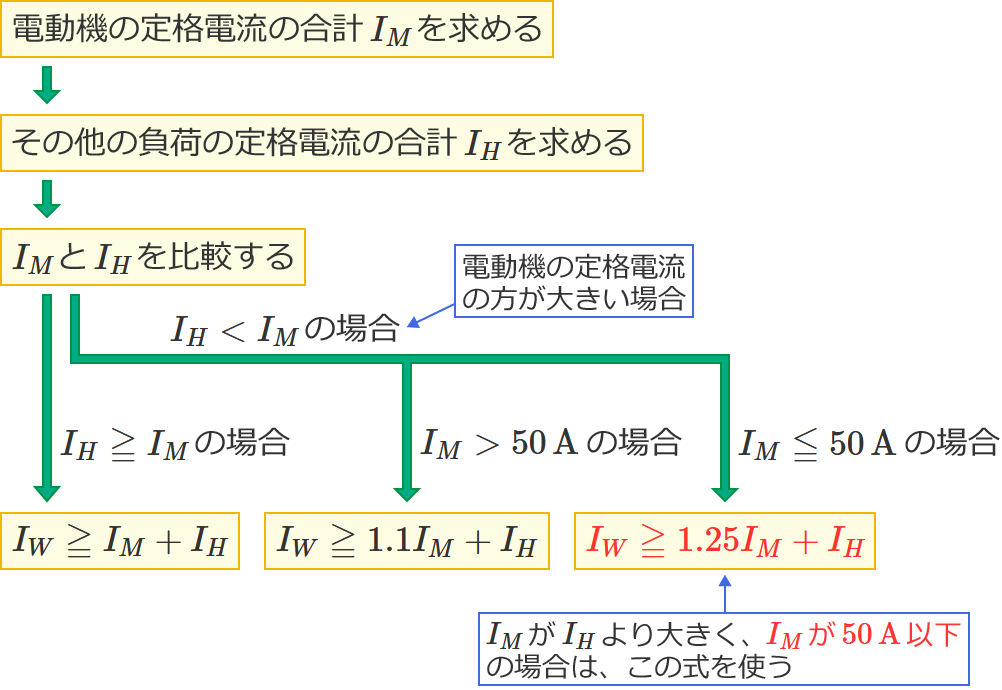
問題1の幹線の太さを決める根拠となる電流の最小値を求める手順

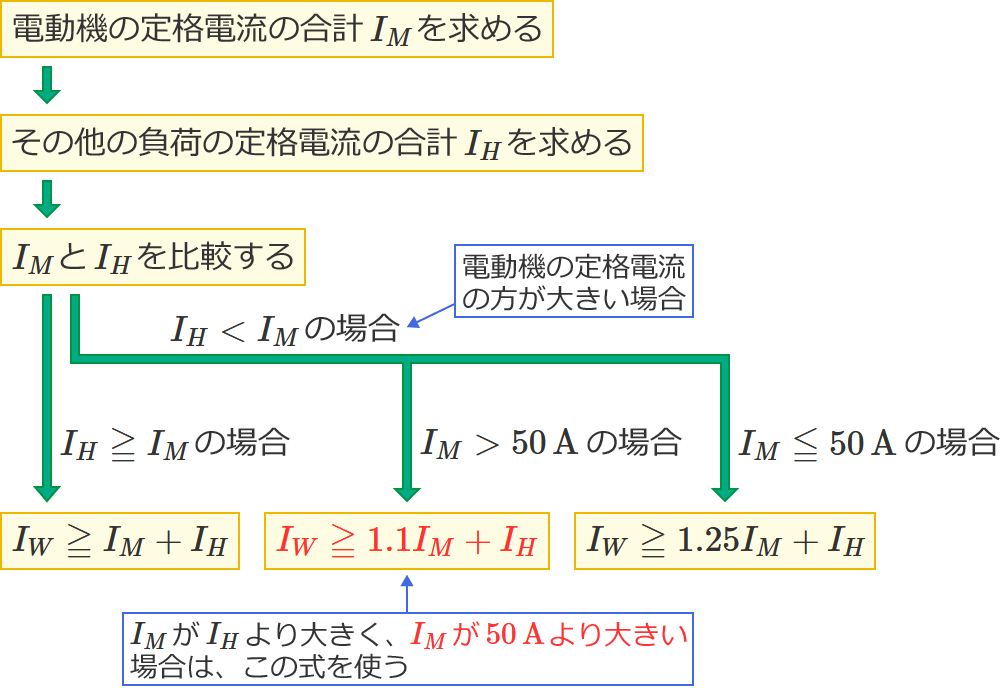
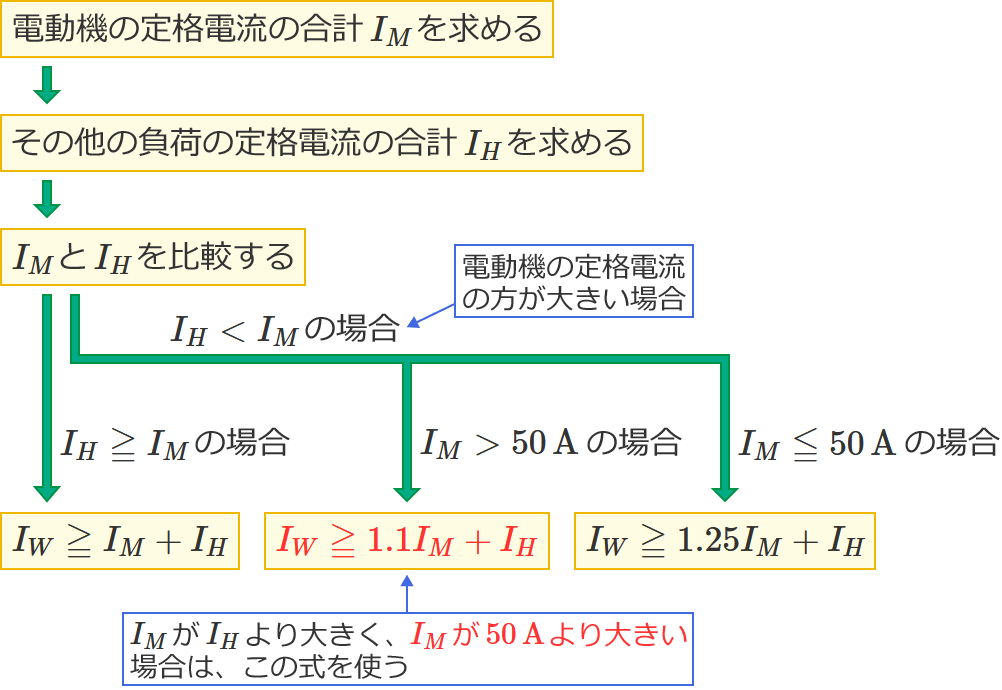
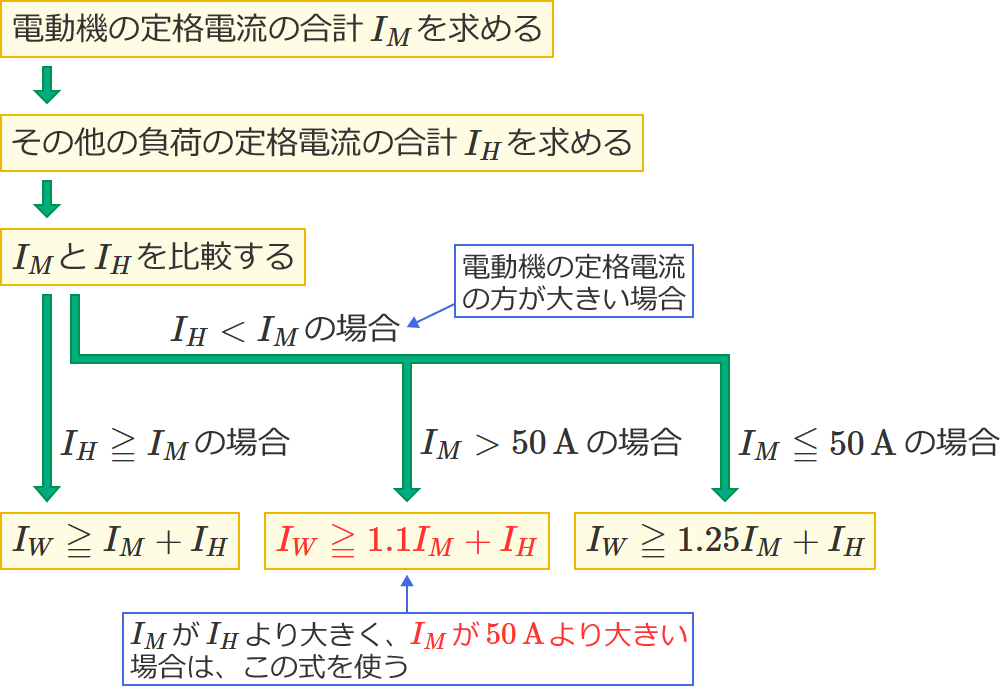
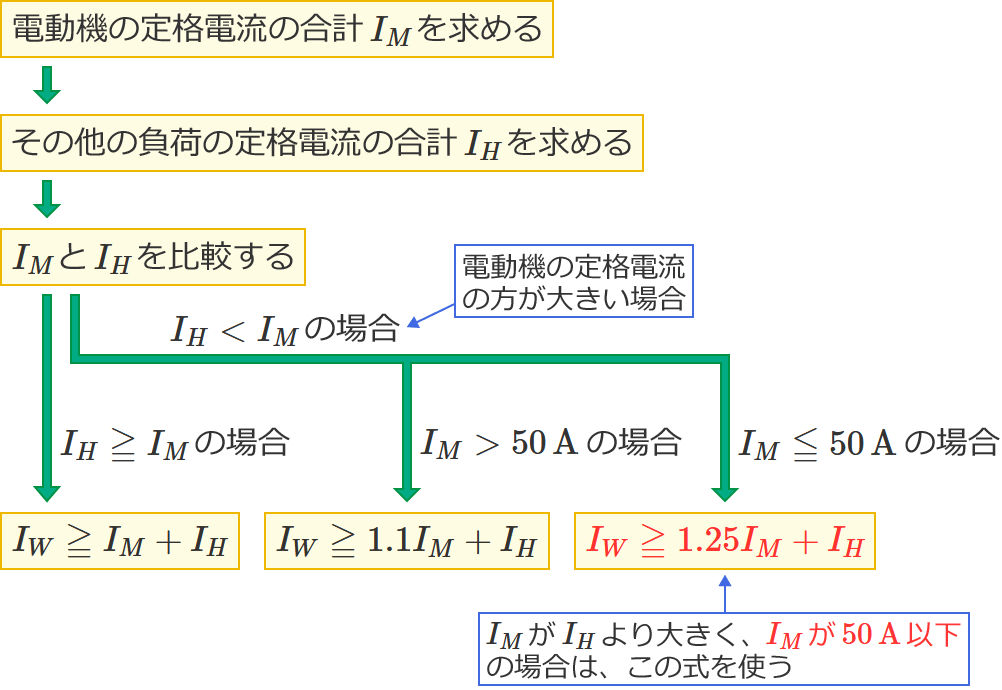
この問題1のような問題で、幹線の太さを決める根拠となる電流の最小値を求める式を選ぶときは、次の2つがポイントになります。

$I_M$ と $I_H$ の大小関係
$I_M$ が $I_H$ より大きい場合は、$I_M$ が $50\,\mathrm{A}$ より大きいか？ $50\,\mathrm{A}$ 以下か？

特に、$I_M$ が $I_H$ より大きい場合は、$I_M$ が $50\,\mathrm{A}$ より大きいか $50\,\mathrm{A}$ 以下かで使う式が異なるので気を付けましょう！（ $I_M$ が $50\,\mathrm{A}$ より大きいときは $I_M$ を $1.1$ 倍する。$I_M$ が $50\,\mathrm{A}$ 以下のときは $I_M$ を $1.25$ 倍する。）

問題2

定格電流 $\boldsymbol{10\,\mathrm{A}}$ の電動機 $\boldsymbol{5}$ 台が接続された単相2線式の低圧屋内幹線がある。この幹線の太さを決定する電流の最小値［$\boldsymbol{\mathrm{A}}$］は？　ただし、需要率は $\boldsymbol{80\,\%}$ とする。
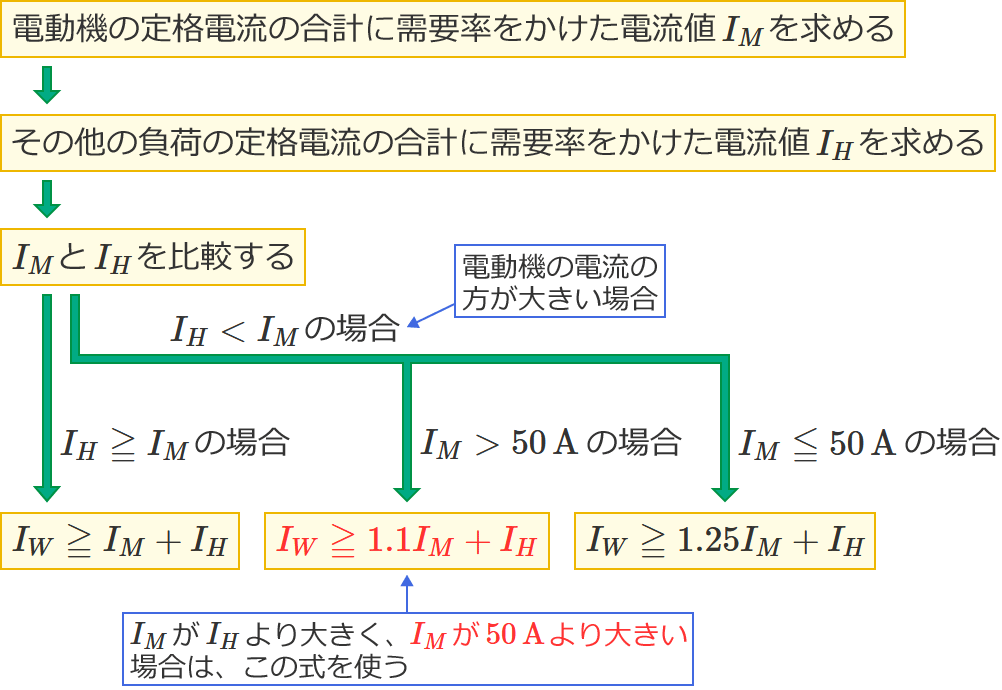
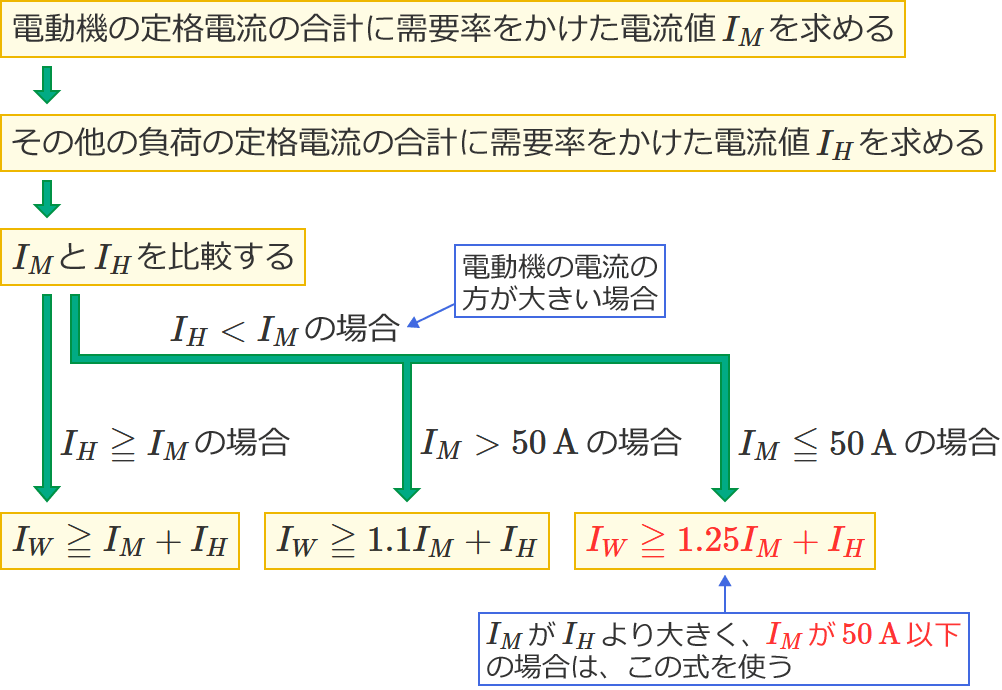
なお、選択肢中の $\boldsymbol{I_M}$ は電動機の定格電流の合計に需要率をかけた電流値［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_H}$ はその他の負荷（電熱器など）の定格電流の合計に需要率をかけた電流値［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_W}$ は求める幹線の太さを決定する電流の最小値［$\boldsymbol{\mathrm{A}}$］です。

$\boldsymbol{I_M=10\times 5\times 0.8=40}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=I_M+I_H}$
$\boldsymbol{=40+0=\color{#f33}{40}}$
$\boldsymbol{I_M=10\times 5\times 0.8=40}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 40+0=\color{#f33}{44}}$
$\boldsymbol{I_M=10\times 5\times 0.8=40}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 40+0=\color{#f33}{50}}$
$\boldsymbol{I_M=10\times 5=50}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 50+0=\color{#f33}{62.5}}$

正解！

はずれ！

解説

正解は、$\boldsymbol{50}$です。
幹線には定格電流 $10\,\mathrm{A}$ の電動機が $5$ 台接続されていて、需要率が $80\,\%$ なので、電動機の定格電流の合計に需要率をかけた電流値 $I_M$ は、$I_M=10\times 5\times 0.8=\color{#f33}{40}\,\mathrm{A}$ になります。
幹線にはその他の負荷（電熱器など）は接続されていないので、その他の負荷の定格電流の合計に需要率をかけた電流値 $I_H$ は、$I_H=\color{#f33}{0}\,\mathrm{A}$ になります。
$I_M$ と $I_H$ を比較すると $I_M$ の方が大きく、$I_M$ は $50\,\mathrm{A}$ 以下なので、幹線の太さを決定する電流の最小値を求める式は $I_W=1.25I_M+I_H$ になります。
この式にぞれぞれの値を代入すると、$I_W=1.25I_M+I_H$ $=1.25\times 40+0$ $=50+0$ $=\color{#f33}{50}$ となるので、求める幹線の太さを決定する電流の最小値は $\color{#f33}{50}\,\mathrm{A}$ になります。

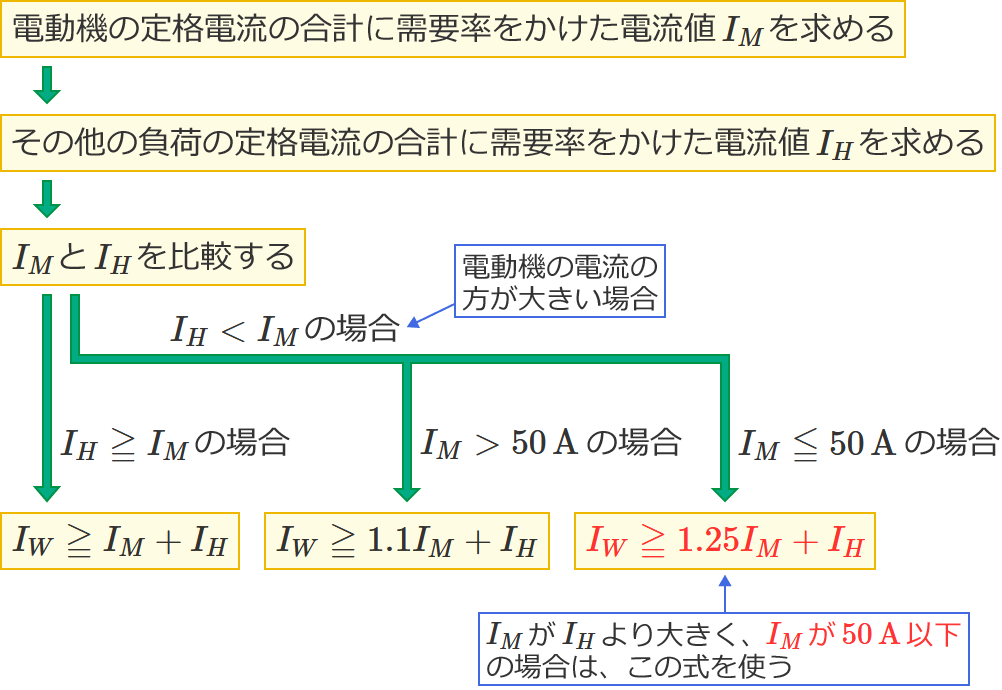
問題2の幹線の太さを決定する電流の最小値を求める手順

この問題2のように、問題文に $100\,\%$ 以外の需要率が示されている場合は、「電動機の定格電流の合計」および「その他の負荷の定格電流の合計」に需要率をかけて、その需要率をかけた値をそれぞれ $I_M$ 、$I_H$ として解いていきます。なお、需要率をかけるときは、例えばこの問題のように需要率が「 $80\,\%$ 」の場合には、$80$ を $100$ で割った「 $0.8$ 」をかけます。

問題3

定格電流 $\boldsymbol{12\,\mathrm{A}}$ の電動機 $\boldsymbol{5}$ 台が接続された単相2線式の低圧屋内幹線がある。この幹線の太さを決定するための根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］は？　ただし、需要率は $\boldsymbol{80\,\%}$ とする。
なお、選択肢中の $\boldsymbol{I_M}$ は電動機の定格電流の合計に需要率をかけた電流値［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_H}$ はその他の負荷（電熱器など）の定格電流の合計に需要率をかけた電流値［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_W}$ は求める幹線の太さを決定するための根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］です。

$\boldsymbol{I_M=12\times 5=60}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 60+0=\color{#f33}{75}}$
$\boldsymbol{I_M=12\times 5\times 0.8=48}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 48+0=\color{#f33}{60}}$
$\boldsymbol{I_M=12\times 5\times 0.6=36}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 36+0=\color{#f33}{39.6}}$
$\boldsymbol{I_M=12\times 5\times 0.4=24}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 24+0=\color{#f33}{26.4}}$

正解！

はずれ！

解説

正解は、$\boldsymbol{60}$です。
幹線には定格電流 $12\,\mathrm{A}$ の電動機が $5$ 台接続されていて、需要率が $80\,\%$ なので、電動機の定格電流の合計に需要率をかけた電流値 $I_M$ は、$I_M=12\times 5\times 0.8=\color{#f33}{48}\,\mathrm{A}$ になります。
幹線にはその他の負荷（電熱器など）は接続されていないので、その他の負荷の定格電流の合計に需要率をかけた電流値 $I_H$ は、$I_H=\color{#f33}{0}\,\mathrm{A}$ になります。
$I_M$ と $I_H$ を比較すると $I_M$ の方が大きく、$I_M$ は $50\,\mathrm{A}$ 以下なので、幹線の太さを決定するための根拠となる電流の最小値を求める式は $I_W=1.25I_M+I_H$ になります。
この式にぞれぞれの値を代入すると、$I_W=1.25I_M+I_H$ $=1.25\times 48+0$ $=60+0$ $=\color{#f33}{60}$ となるので、求める幹線の太さを決定するための根拠となる電流の最小値は $\color{#f33}{60}\,\mathrm{A}$ になります。

問題3の幹線の太さを決定するための根拠となる電流の最小値を求める手順

問題4

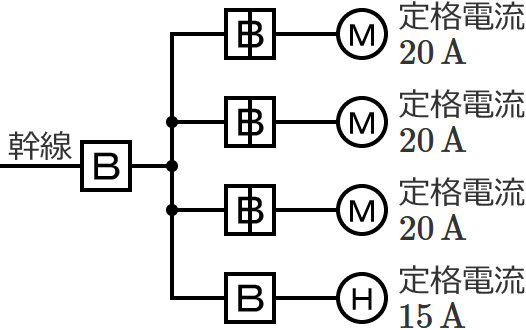
問題4の配線図

$\boldsymbol{I_M=20+20+20=60}$
$\boldsymbol{I_H=15}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 60+15=\color{#f33}{81}}$
$\boldsymbol{I_M=20+20=40}$
$\boldsymbol{I_H=20+15=35}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 40+35=\color{#f33}{79}}$
$\boldsymbol{I_M=20+20+20=60}$
$\boldsymbol{I_H=15}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 60+15=\color{#f33}{90}}$
$\boldsymbol{I_M=20+20=40}$
$\boldsymbol{I_H=20+15=35}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 40+35=\color{#f33}{85}}$

正解！

はずれ！

解説

正解は、$\boldsymbol{81}$です。
幹線には定格電流 $20\,\mathrm{A}$ の電動機が $3$ 台接続されているので、電動機の定格電流の合計 $I_M$ は、$I_M=20+20+20=\color{#f33}{60}\,\mathrm{A}$ になります。
幹線には定格電流 $15\,\mathrm{A}$ の電熱器が $1$ 台接続されているので、電熱器（その他の負荷）の定格電流の合計 $I_H$ は、$I_H=\color{#f33}{15}\,\mathrm{A}$ になります。

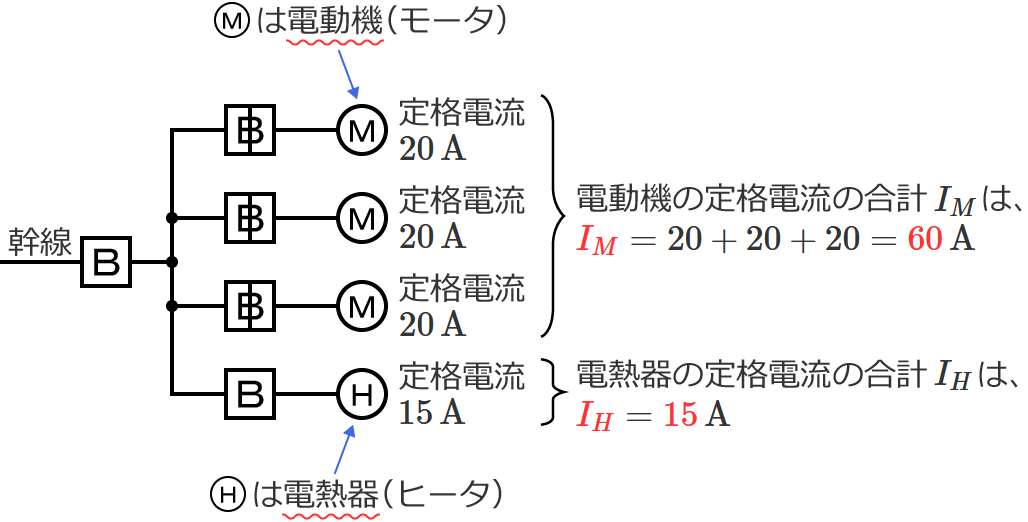
問題4の電動機と電熱器それぞれの定格電流の合計

$I_M$ と $I_H$ を比較すると $I_M$ の方が大きく、$I_M$ は $50\,\mathrm{A}$ より大きいので、幹線の太さを決める根拠となる電流の最小値を求める式は $I_W=1.1I_M+I_H$ になります。
この式にぞれぞれの値を代入すると、$I_W=1.1I_M+I_H$ $=1.1\times 60+15$ $=66+15$ $=\color{#f33}{81}$ となるので、求める幹線の太さを決める根拠となる電流の最小値は $\color{#f33}{81}\,\mathrm{A}$ になります。

問題4の幹線の太さを決める根拠となる電流の最小値を求める手順

問題5

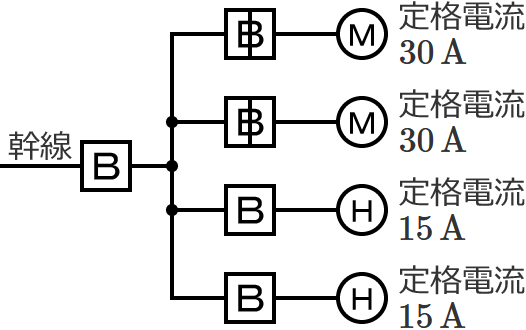
図のように、三相電動機と三相電熱器が低圧屋内幹線に接続されている場合、幹線の太さを決める根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］は？　ただし、需要率は $\boldsymbol{100\,\%}$ とする。
なお、選択肢中の $\boldsymbol{I_M}$ は電動機の定格電流の合計［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_H}$ は電熱器（その他の負荷）の定格電流の合計［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_W}$ は求める幹線の太さを決める根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］です。

問題5の配線図

$\boldsymbol{I_M=30+30=60}$
$\boldsymbol{I_H=15+15=30}$
$\boldsymbol{I_W=I_M+I_H}$
$\boldsymbol{=60+30=\color{#f33}{90}}$
$\boldsymbol{I_M=30+30=60}$
$\boldsymbol{I_H=15+15=30}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 60+30=\color{#f33}{96}}$
$\boldsymbol{I_M=30+30=60}$
$\boldsymbol{I_H=15+15=30}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 60+30=\color{#f33}{105}}$
$\boldsymbol{I_M=30+15=45}$
$\boldsymbol{I_H=15}$
$\boldsymbol{I_W=I_M+I_H}$
$\boldsymbol{=45+15=\color{#f33}{60}}$

正解！

はずれ！

解説

正解は、$\boldsymbol{96}$です。
幹線には定格電流 $30\,\mathrm{A}$ の電動機が $2$ 台接続されているので、電動機の定格電流の合計 $I_M$ は、$I_M=30+30=\color{#f33}{60}\,\mathrm{A}$ になります。
幹線には定格電流 $15\,\mathrm{A}$ の電熱器が $2$ 台接続されているので、電熱器（その他の負荷）の定格電流の合計 $I_H$ は、$I_H=15+15=\color{#f33}{30}\,\mathrm{A}$ になります。

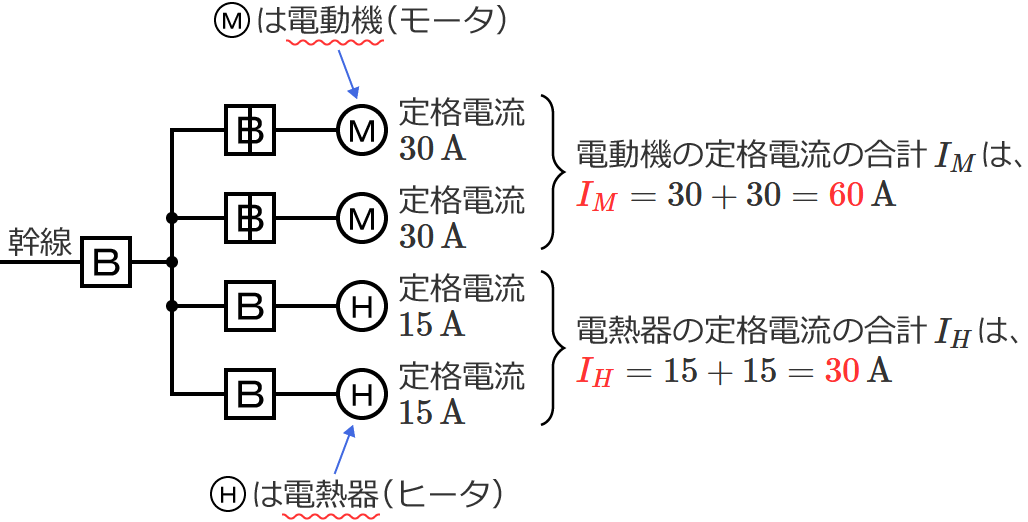
問題5の電動機と電熱器それぞれの定格電流の合計

$I_M$ と $I_H$ を比較すると $I_M$ の方が大きく、$I_M$ は $50\,\mathrm{A}$ より大きいので、幹線の太さを決める根拠となる電流の最小値を求める式は $I_W=1.1I_M+I_H$ になります。
この式にぞれぞれの値を代入すると、$I_W=1.1I_M+I_H$ $=1.1\times 60+30$ $=66+30$ $=\color{#f33}{96}$ となるので、求める幹線の太さを決める根拠となる電流の最小値は $\color{#f33}{96}\,\mathrm{A}$ になります。

問題5の幹線の太さを決める根拠となる電流の最小値を求める手順

問題6

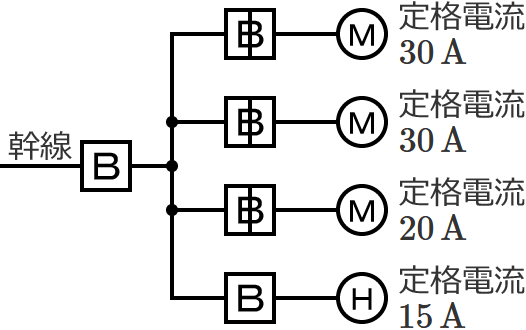
問題6の配線図

$\boldsymbol{I_M=30}$
$\boldsymbol{I_H=15}$
$\boldsymbol{I_W=I_M+I_H}$
$\boldsymbol{=30+15=\color{#f33}{45}}$
$\boldsymbol{I_M=30+30+20=80}$
$\boldsymbol{I_H=15}$
$\boldsymbol{I_W=I_M+I_H}$
$\boldsymbol{=80+15=\color{#f33}{95}}$
$\boldsymbol{I_M=30+30+20=80}$
$\boldsymbol{I_H=15}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 80+15=\color{#f33}{103}}$
$\boldsymbol{I_M=30+30+20=80}$
$\boldsymbol{I_H=15}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 80+15=\color{#f33}{115}}$

正解！

はずれ！

解説

正解は、$\boldsymbol{103}$です。
幹線には定格電流 $30\,\mathrm{A}$ の電動機が $2$ 台、定格電流 $20\,\mathrm{A}$ の電動機が $1$ 台接続されているので、電動機の定格電流の合計 $I_M$ は、$I_M=30+30+20=\color{#f33}{80}\,\mathrm{A}$ になります。
幹線には定格電流 $15\,\mathrm{A}$ の電熱器が $1$ 台接続されているので、電熱器（その他の負荷）の定格電流の合計 $I_H$ は、$I_H=\color{#f33}{15}\,\mathrm{A}$ になります。

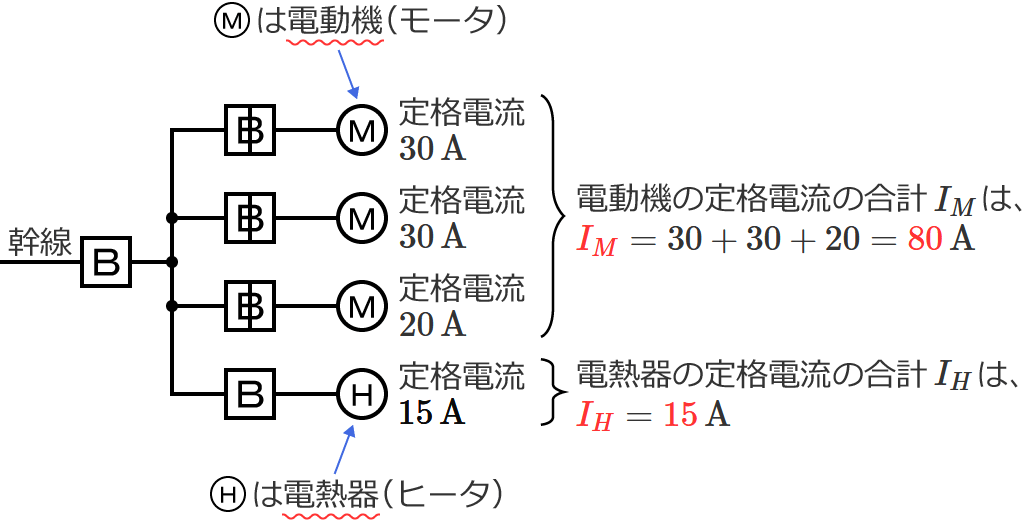
問題6の電動機と電熱器それぞれの定格電流の合計

$I_M$ と $I_H$ を比較すると $I_M$ の方が大きく、$I_M$ は $50\,\mathrm{A}$ より大きいので、幹線の太さを決める根拠となる電流の最小値を求める式は $I_W=1.1I_M+I_H$ になります。
この式にぞれぞれの値を代入すると、$I_W=1.1I_M+I_H$ $=1.1\times 80+15$ $=88+15$ $=\color{#f33}{103}$ となるので、求める幹線の太さを決める根拠となる電流の最小値は $\color{#f33}{103}\,\mathrm{A}$ になります。

問題6の幹線の太さを決める根拠となる電流の最小値を求める手順

問題7

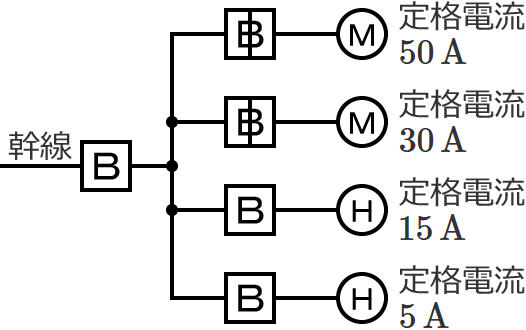
問題7の配線図

$\boldsymbol{I_M=50+30=80}$
$\boldsymbol{I_H=15+5=20}$
$\boldsymbol{I_W=I_M+I_H}$
$\boldsymbol{=80+20=\color{#f33}{100}}$
$\boldsymbol{I_M=50+30=80}$
$\boldsymbol{I_H=15+5=20}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 80+20=\color{#f33}{108}}$
$\boldsymbol{I_M=50+30=80}$
$\boldsymbol{I_H=15+5=20}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 80+20=\color{#f33}{120}}$
$\boldsymbol{I_M=50}$
$\boldsymbol{I_H=15}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 50+15=\color{#f33}{77.5}}$

正解！

はずれ！

解説

正解は、$\boldsymbol{108}$です。
幹線には定格電流 $50\,\mathrm{A}$ の電動機が $1$ 台、定格電流 $30\,\mathrm{A}$ の電動機が $1$ 台接続されているので、電動機の定格電流の合計 $I_M$ は、$I_M=50+30=\color{#f33}{80}\,\mathrm{A}$ になります。
幹線には定格電流 $15\,\mathrm{A}$ の電熱器が $1$ 台、定格電流 $5\,\mathrm{A}$ の電熱器が $1$ 台接続されているので、電熱器（その他の負荷）の定格電流の合計 $I_H$ は、$I_H=15+5=\color{#f33}{20}\,\mathrm{A}$ になります。

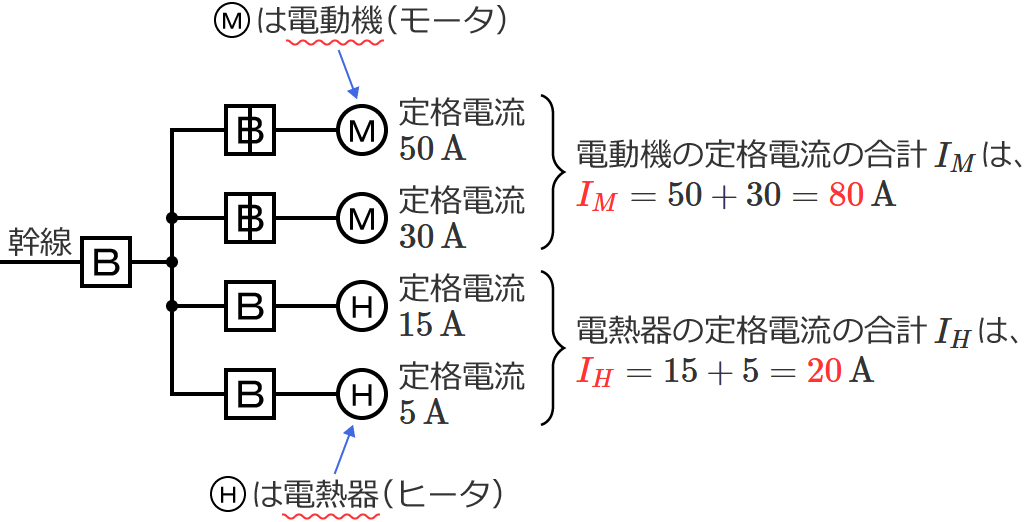
問題7の電動機と電熱器それぞれの定格電流の合計

$I_M$ と $I_H$ を比較すると $I_M$ の方が大きく、$I_M$ は $50\,\mathrm{A}$ より大きいので、幹線の太さを決める根拠となる電流の最小値を求める式は $I_W=1.1I_M+I_H$ になります。
この式にぞれぞれの値を代入すると、$I_W=1.1I_M+I_H$ $=1.1\times 80+20$ $=88+20$ $=\color{#f33}{108}$ となるので、求める幹線の太さを決める根拠となる電流の最小値は $\color{#f33}{108}\,\mathrm{A}$ になります。

問題7の幹線の太さを決める根拠となる電流の最小値を求める手順

問題8

定格電流 $\boldsymbol{10\,\mathrm{A}}$ の電動機 $\boldsymbol{10}$ 台が接続された単相2線式の低圧屋内幹線がある。この幹線の太さを決定する電流の最小値［$\boldsymbol{\mathrm{A}}$］は？　ただし、需要率は $\boldsymbol{80\,\%}$ とする。
なお、選択肢中の $\boldsymbol{I_M}$ は電動機の定格電流の合計に需要率をかけた電流値［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_H}$ はその他の負荷（電熱器など）の定格電流の合計に需要率をかけた電流値［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_W}$ は求める幹線の太さを決定する電流の最小値［$\boldsymbol{\mathrm{A}}$］です。

$\boldsymbol{I_M=10\times 10\times 0.2=20}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 20+0=\color{#f33}{25}}$
$\boldsymbol{I_M=10\times 10\times 0.8=80}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 80+0=\color{#f33}{100}}$
$\boldsymbol{I_M=10\times 10\times 0.2=20}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 20+0=\color{#f33}{22}}$
$\boldsymbol{I_M=10\times 10\times 0.8=80}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 80+0=\color{#f33}{88}}$

正解！

はずれ！

解説

正解は、$\boldsymbol{88}$です。
幹線には定格電流 $10\,\mathrm{A}$ の電動機が $10$ 台接続されていて、需要率が $80\,\%$ なので、電動機の定格電流の合計に需要率をかけた電流値 $I_M$ は、$I_M=10\times 10\times 0.8=\color{#f33}{80}\,\mathrm{A}$ になります。
幹線にはその他の負荷（電熱器など）は接続されていないので、その他の負荷の定格電流の合計に需要率をかけた電流値 $I_H$ は、$I_H=\color{#f33}{0}\,\mathrm{A}$ になります。
$I_M$ と $I_H$ を比較すると $I_M$ の方が大きく、$I_M$ は $50\,\mathrm{A}$ より大きいので、幹線の太さを決定する電流の最小値を求める式は $I_W=1.1I_M+I_H$ になります。
この式にぞれぞれの値を代入すると、$I_W=1.1I_M+I_H$ $=1.1\times 80+0$ $=88+0$ $=\color{#f33}{88}$ となるので、求める幹線の太さを決定する電流の最小値は $\color{#f33}{88}\,\mathrm{A}$ になります。

問題8の幹線の太さを決定する電流の最小値を求める手順

問題9

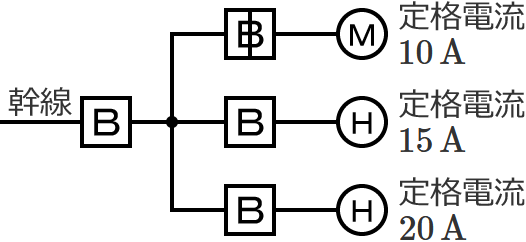
問題9の配線図

$\boldsymbol{I_M=10}$
$\boldsymbol{I_H=15+20=35}$
$\boldsymbol{I_W=I_M+I_H}$
$\boldsymbol{=10+35=\color{#f33}{45}}$
$\boldsymbol{I_M=10}$
$\boldsymbol{I_H=15+20=35}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 10+35=\color{#f33}{46}}$
$\boldsymbol{I_M=10}$
$\boldsymbol{I_H=15+20=35}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 10+35=\color{#f33}{47.5}}$
$\boldsymbol{I_M=15+20=35}$
$\boldsymbol{I_H=10}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 35+10=\color{#f33}{48.5}}$

正解！

はずれ！

解説

正解は、$\boldsymbol{45}$です。
幹線には定格電流 $10\,\mathrm{A}$ の電動機が $1$ 台接続されているので、電動機の定格電流の合計 $I_M$ は、$I_M=\color{#f33}{10}\,\mathrm{A}$ になります。
幹線には定格電流 $15\,\mathrm{A}$ の電熱器が $1$ 台、定格電流 $20\,\mathrm{A}$ の電熱器が $1$ 台接続されているので、電熱器（その他の負荷）の定格電流の合計 $I_H$ は、$I_H=15+20=\color{#f33}{35}\,\mathrm{A}$ になります。

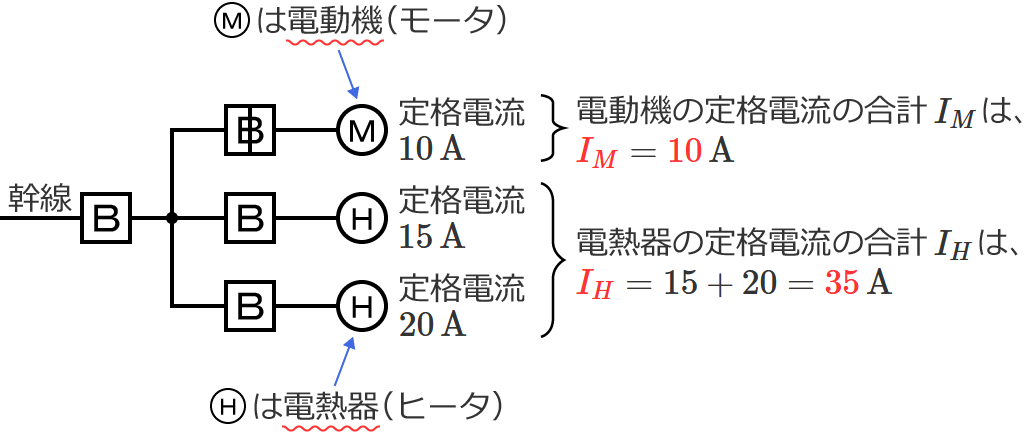
問題9の電動機と電熱器それぞれの定格電流の合計

$I_M$ と $I_H$ を比較すると $I_M$ が $I_H$ 以下なので、幹線の太さを決める根拠となる電流の最小値を求める式は $I_W=I_M+I_H$ になります。
この式にぞれぞれの値を代入すると、$I_W=I_M+I_H$ $=10+35$ $=\color{#f33}{45}$ となるので、求める幹線の太さを決める根拠となる電流の最小値は $\color{#f33}{45}\,\mathrm{A}$ になります。

問題9の幹線の太さを決める根拠となる電流の最小値を求める手順

問題10

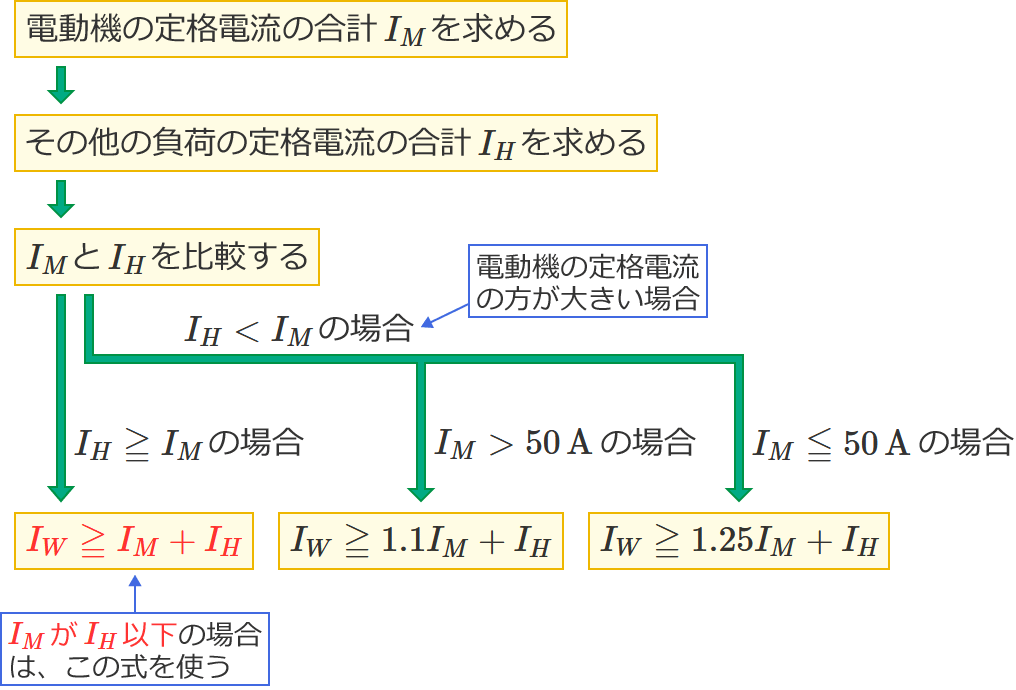
図のように、三相電動機と三相電熱器が幹線に接続されている場合、幹線の太さを決める根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］は？　ただし、需要率は $\boldsymbol{100\,\%}$ とする。
なお、選択肢中の $\boldsymbol{I_M}$ は電動機の定格電流の合計［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_H}$ は電熱器（その他の負荷）の定格電流の合計［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_W}$ は求める幹線の太さを決める根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］です。

問題10の配線図

$\boldsymbol{I_M=10+10=20}$
$\boldsymbol{I_H=20+20=40}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 20+40=\color{#f33}{65}}$
$\boldsymbol{I_M=20+20=40}$
$\boldsymbol{I_H=10+10=20}$
$\boldsymbol{I_W=I_M+I_H}$
$\boldsymbol{=40+20=\color{#f33}{60}}$
$\boldsymbol{I_M=20+20=40}$
$\boldsymbol{I_H=10+10=20}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 40+20=\color{#f33}{64}}$
$\boldsymbol{I_M=20+20=40}$
$\boldsymbol{I_H=10+10=20}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 40+20=\color{#f33}{70}}$

正解！

はずれ！

解説

正解は、$\boldsymbol{70}$です。
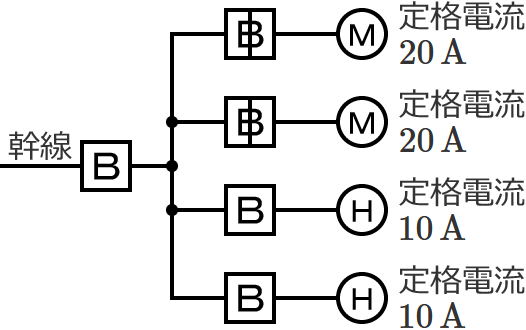
幹線には定格電流 $20\,\mathrm{A}$ の電動機が $2$ 台接続されているので、電動機の定格電流の合計 $I_M$ は、$I_M=20+20=\color{#f33}{40}\,\mathrm{A}$ になります。
幹線には定格電流 $10\,\mathrm{A}$ の電熱器が $2$ 台接続されているので、電熱器（その他の負荷）の定格電流の合計 $I_H$ は、$I_H=10+10=\color{#f33}{20}\,\mathrm{A}$ になります。

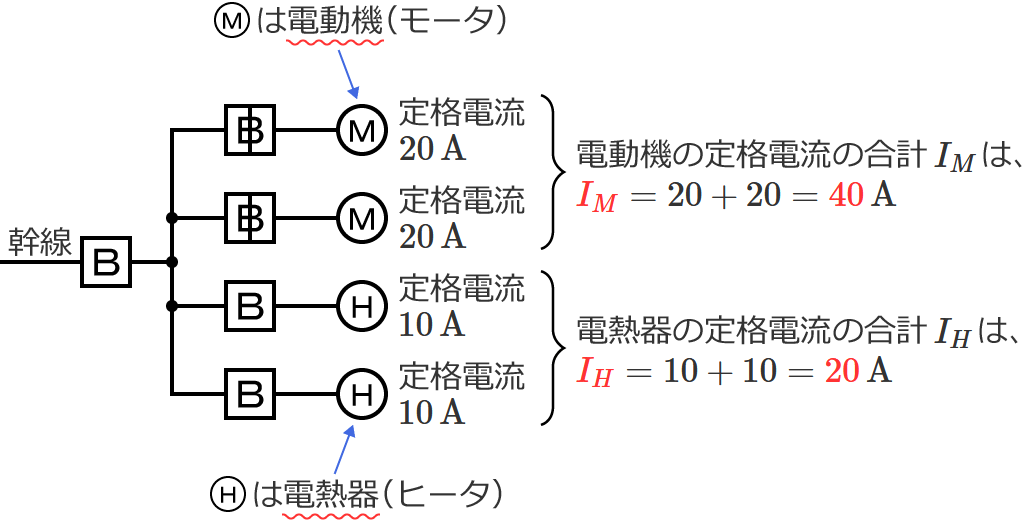
問題10の電動機と電熱器それぞれの定格電流の合計

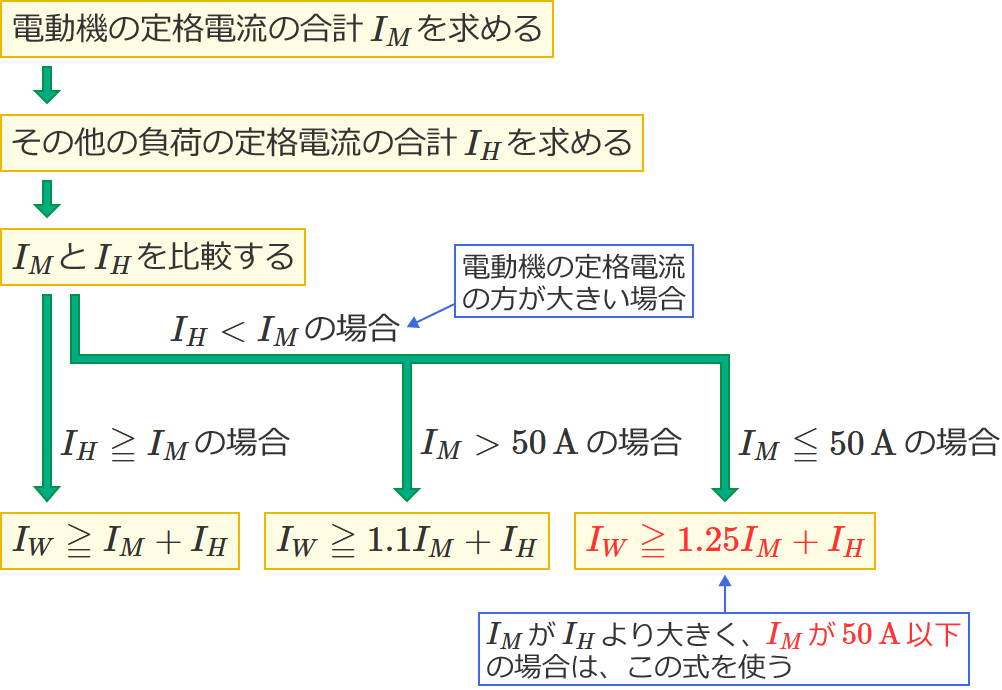
$I_M$ と $I_H$ を比較すると $I_M$ の方が大きく、$I_M$ は $50\,\mathrm{A}$ 以下なので、幹線の太さを決める根拠となる電流の最小値を求める式は $I_W=1.25I_M+I_H$ になります。
この式にぞれぞれの値を代入すると、$I_W=1.25I_M+I_H$ $=1.25\times 40+20$ $=50+20$ $=\color{#f33}{70}$ となるので、求める幹線の太さを決める根拠となる電流の最小値は $\color{#f33}{70}\,\mathrm{A}$ になります。

問題10の幹線の太さを決める根拠となる電流の最小値を求める手順

問題11

定格電流がそれぞれ $\boldsymbol{20\,\mathrm{A}}$ および $\boldsymbol{8\,\mathrm{A}}$ の電動機各 $\boldsymbol{1}$ 台を接続した低圧屋内幹線がある。この幹線の太さを決める根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］は？　ただし、需要率は $\boldsymbol{100\,\%}$ とする。
なお、選択肢中の $\boldsymbol{I_M}$ は電動機の定格電流の合計［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_H}$ はその他の負荷（電熱器など）の定格電流の合計［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_W}$ は求める幹線の太さを決める根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］です。

$\boldsymbol{I_M=20}$
$\boldsymbol{I_H=8}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 20+8=\color{#f33}{33}}$
$\boldsymbol{I_M=8}$
$\boldsymbol{I_H=20}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 8+20=\color{#f33}{30}}$
$\boldsymbol{I_M=0}$
$\boldsymbol{I_H=20+8=28}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 0+28=\color{#f33}{28}}$
$\boldsymbol{I_M=20+8=28}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 28+0=\color{#f33}{35}}$

正解！

はずれ！

解説

正解は、$\boldsymbol{35}$です。
幹線には定格電流 $20\,\mathrm{A}$ の電動機が $1$ 台、定格電流 $8\,\mathrm{A}$ の電動機が $1$ 台接続されているので、電動機の定格電流の合計 $I_M$ は、$I_M=20+8=\color{#f33}{28}\,\mathrm{A}$ になります。
幹線にはその他の負荷（電熱器など）は接続されていないので、その他の負荷の定格電流の合計 $I_H$ は、$I_H=\color{#f33}{0}\,\mathrm{A}$ になります。
$I_M$ と $I_H$ を比較すると $I_M$ の方が大きく、$I_M$ は $50\,\mathrm{A}$ 以下なので、幹線の太さを決める根拠となる電流の最小値を求める式は $I_W=1.25I_M+I_H$ になります。
この式にぞれぞれの値を代入すると、$I_W=1.25I_M+I_H$ $=1.25\times 28+0$ $=35+0$ $=\color{#f33}{35}$ となるので、求める幹線の太さを決める根拠となる電流の最小値は $\color{#f33}{35}\,\mathrm{A}$ になります。

問題11の幹線の太さを決める根拠となる電流の最小値を求める手順

問題12

定格電流 $\boldsymbol{8\,\mathrm{A}}$ の電動機 $\boldsymbol{8}$ 台に1回線の低圧屋内幹線で電力を供給する場合、その幹線の太さを決める根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］は？　ただし、需要率は $\boldsymbol{75\,\%}$ とする。
なお、選択肢中の $\boldsymbol{I_M}$ は電動機の定格電流の合計に需要率をかけた電流値［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_H}$ はその他の負荷（電熱器など）の定格電流の合計に需要率をかけた電流値［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_W}$ は求める幹線の太さを決める根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］です。

$\boldsymbol{I_M=8\times 8\times 0.25=16}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 16+0=\color{#f33}{20}}$
$\boldsymbol{I_M=8\times 8\times 0.75=48}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 48+0=\color{#f33}{60}}$
$\boldsymbol{I_M=8\times 8\times 0.25=16}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=I_M+I_H}$
$\boldsymbol{=16+0=\color{#f33}{16}}$
$\boldsymbol{I_M=8\times 8\times 0.75=48}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=I_M+I_H}$
$\boldsymbol{=48+0=\color{#f33}{48}}$

正解！

はずれ！

解説

正解は、$\boldsymbol{60}$です。
幹線には定格電流 $8\,\mathrm{A}$ の電動機が $8$ 台接続されていて、需要率が $75\,\%$ なので、電動機の定格電流の合計に需要率をかけた電流値 $I_M$ は、$I_M=8\times 8\times 0.75=\color{#f33}{48}\,\mathrm{A}$ になります。
幹線にはその他の負荷（電熱器など）は接続されていないので、その他の負荷の定格電流の合計に需要率をかけた電流値 $I_H$ は、$I_H=\color{#f33}{0}\,\mathrm{A}$ になります。
$I_M$ と $I_H$ を比較すると $I_M$ の方が大きく、$I_M$ は $50\,\mathrm{A}$ 以下なので、幹線の太さを決める根拠となる電流の最小値を求める式は $I_W=1.25I_M+I_H$ になります。
この式にぞれぞれの値を代入すると、$I_W=1.25I_M+I_H$ $=1.25\times 48+0$ $=60+0$ $=\color{#f33}{60}$ となるので、求める幹線の太さを決める根拠となる電流の最小値は $\color{#f33}{60}\,\mathrm{A}$ になります。

問題12の幹線の太さを決める根拠となる電流の最小値を求める手順

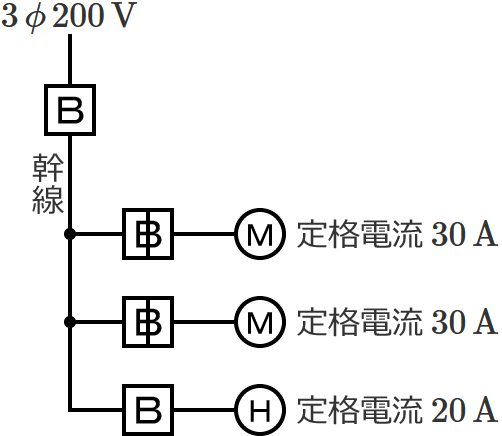
問題13

図のような電動機と電熱器に電力を供給する低圧屋内幹線がある。この幹線の電線の太さを決める根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］は？　ただし、需要率は $\boldsymbol{100\,\%}$ とする。
なお、選択肢中の $\boldsymbol{I_M}$ は電動機の定格電流の合計［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_H}$ は電熱器（その他の負荷）の定格電流の合計［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_W}$ は求める幹線の電線の太さを決める根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］です。

問題13の配線図

$\boldsymbol{I_M=30+30=60}$
$\boldsymbol{I_H=20}$
$\boldsymbol{I_W=I_M+I_H}$
$\boldsymbol{=60+20=\color{#f33}{80}}$
$\boldsymbol{I_M=30+30=60}$
$\boldsymbol{I_H=20}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 60+20=\color{#f33}{86}}$
$\boldsymbol{I_M=30+30=60}$
$\boldsymbol{I_H=20}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 60+20=\color{#f33}{95}}$
$\boldsymbol{I_M=30+30+20=80}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 80+0=\color{#f33}{100}}$

正解！

はずれ！

解説

正解は、$\boldsymbol{86}$です。
幹線には定格電流 $30\,\mathrm{A}$ の電動機が $2$ 台接続されているので、電動機の定格電流の合計 $I_M$ は、$I_M=30+30=\color{#f33}{60}\,\mathrm{A}$ になります。
幹線には定格電流 $20\,\mathrm{A}$ の電熱器が $1$ 台接続されているので、電熱器（その他の負荷）の定格電流の合計 $I_H$ は、$I_H=\color{#f33}{20}\,\mathrm{A}$ になります。

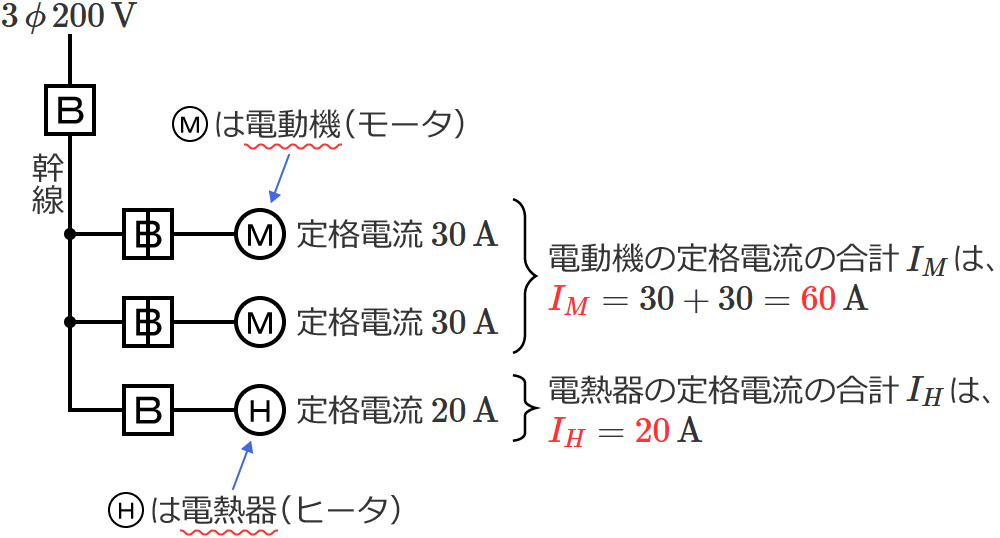
問題13の電動機と電熱器それぞれの定格電流の合計

$I_M$ と $I_H$ を比較すると $I_M$ の方が大きく、$I_M$ は $50\,\mathrm{A}$ より大きいので、幹線の電線の太さを決める根拠となる電流の最小値を求める式は $I_W=1.1I_M+I_H$ になります。
この式にぞれぞれの値を代入すると、$I_W=1.1I_M+I_H$ $=1.1\times 60+20$ $=66+20$ $=\color{#f33}{86}$ となるので、求める幹線の電線の太さを決める根拠となる電流の最小値は $\color{#f33}{86}\,\mathrm{A}$ になります。

問題13の幹線の電線の太さを決める根拠となる電流の最小値を求める手順

問題14

定格電流 $\boldsymbol{20\,\mathrm{A}}$ の電動機 $\boldsymbol{2}$ 台と定格電流 $\boldsymbol{30\,\mathrm{A}}$ の電動機 $\boldsymbol{1}$ 台に1つの低圧屋内幹線で電力を供給する場合、その幹線の太さを決める根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］は？　ただし、需要率は $\boldsymbol{100\,\%}$ とする。
なお、選択肢中の $\boldsymbol{I_M}$ は電動機の定格電流の合計［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_H}$ はその他の負荷（電熱器など）の定格電流の合計［$\boldsymbol{\mathrm{A}}$］、$\boldsymbol{I_W}$ は求める幹線の太さを決める根拠となる電流の最小値［$\boldsymbol{\mathrm{A}}$］です。

$\boldsymbol{I_M=20\times 2+30=70}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=I_M+I_H}$
$\boldsymbol{=70+0=\color{#f33}{70}}$
$\boldsymbol{I_M=20\times 2=40}$
$\boldsymbol{I_H=30}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 40+30=\color{#f33}{74}}$
$\boldsymbol{I_M=20\times 2+30=70}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.1I_M+I_H}$
$\boldsymbol{=1.1\times 70+0=\color{#f33}{77}}$
$\boldsymbol{I_M=20\times 2+30=70}$
$\boldsymbol{I_H=0}$
$\boldsymbol{I_W=1.25I_M+I_H}$
$\boldsymbol{=1.25\times 70+0=\color{#f33}{87.5}}$

正解！

はずれ！

解説

正解は、$\boldsymbol{77}$です。
幹線には定格電流 $20\,\mathrm{A}$ の電動機が $2$ 台、定格電流 $30\,\mathrm{A}$ の電動機が $1$ 台接続されているので、電動機の定格電流の合計 $I_M$ は、$I_M=20\times 2+30=\color{#f33}{70}\,\mathrm{A}$ になります。
幹線にはその他の負荷（電熱器など）は接続されていないので、その他の負荷の定格電流の合計 $I_H$ は、$I_H=\color{#f33}{0}\,\mathrm{A}$ になります。
$I_M$ と $I_H$ を比較すると $I_M$ の方が大きく、$I_M$ は $50\,\mathrm{A}$ より大きいので、幹線の太さを決める根拠となる電流の最小値を求める式は $I_W=1.1I_M+I_H$ になります。
この式にぞれぞれの値を代入すると、$I_W=1.1I_M+I_H$ $=1.1\times 70+0$ $=77+0$ $=\color{#f33}{77}$ となるので、求める幹線の太さを決める根拠となる電流の最小値は $\color{#f33}{77}\,\mathrm{A}$ になります。

問題14の幹線の太さを決める根拠となる電流の最小値を求める手順

第二種電気工事士学科試験の4択クイズのまとめページ（一覧）はこちら
⇒　第二種電気工事士学科試験の4択クイズ

2024年版第二種電気工事士試験学科試験過去問題集

－佐藤共史・著　技術評論社－

過去10年分の過去問題と詳しい解説を掲載している過去問題集です。学科試験で出題される内容の要点をまとめた「学科試験の要点まとめ」も掲載！
2024年度の学科試験対策におすすめです！

アマゾンで見る

楽天で見る

ヤフーショッピングで見る

このページの問題文には、（一財）電気技術者試験センターが作成した第二種電気工事士学科試験の試験問題から一部抜粋した文章を使用しています。

第二種電気工事士学科試験の4択クイズ電線の許容電流　←BACK

NEXT→　第二種電気工事士学科試験の4択クイズ分岐回路の開閉器および過電流遮断器の施設

第二種電気工事士学科試験の4択クイズ幹線の太さを決める根拠となる電流の最小値　関連ページ

4択クイズ鑑別スイッチ: 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「スイッチ」についての4択クイズです。
4択クイズ鑑別コンセント: 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「コンセント」についての4択クイズです。
4択クイズ鑑別遮断器と開閉器: 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「遮断器と開閉器」についての4択クイズです。
4択クイズ鑑別照明器具: 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「照明器具」についての4択クイズです。
4択クイズ鑑別電線管工事で使う材料: 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「電線管工事で使う材料」についての4択クイズです。
4択クイズ鑑別電線・ケーブルと電線を接続する材料: 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「電線・ケーブルと電線を接続する材料」についての4択クイズです。
4択クイズ鑑別その他の機器・器具・材料: 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「その他の機器・器具・材料」についての4択クイズです。
4択クイズ鑑別電気工事で使う工具: 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「電気工事で使う工具」についての4択クイズです。
4択クイズ鑑別測定器: 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「測定器」についての4択クイズです。
4択クイズ接地工事: 第二種電気工事士学科試験で出題されている「接地工事」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズケーブル工事: 第二種電気工事士学科試験で出題されている「ケーブル工事」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ地中埋設工事: 第二種電気工事士学科試験で出題されている「地中埋設工事」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ金属管工事: 第二種電気工事士学科試験で出題されている「金属管工事」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ金属可とう電線管工事: 第二種電気工事士学科試験で出題されている「金属可とう電線管工事」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ合成樹脂管工事: 第二種電気工事士学科試験で出題されている「合成樹脂管工事」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ金属線ぴ工事: 第二種電気工事士学科試験で出題されている「金属線ぴ工事」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ金属・フロア・ライティングダクト工事: 第二種電気工事士学科試験で出題されている「金属ダクト工事、フロアダクト工事、ライティングダクト工事」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズネオン放電灯工事: 第二種電気工事士学科試験で出題されている「ネオン放電灯工事」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズショウウィンドー・ショウケース内工事: 第二種電気工事士学科試験で出題されている「ショウウィンドー・ショウケース内工事」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ小勢力回路の工事: 第二種電気工事士学科試験で出題されている「小勢力回路の工事」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ低圧屋内配線工事と施工できる場所: 第二種電気工事士学科試験で出題されている「低圧屋内配線工事と施工できる場所」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ特殊な場所の工事と施工できる場所: 第二種電気工事士学科試験で出題されている「特殊な場所の工事と施工できる場所」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ三相誘導電動機のスターデルタ始動法: 第二種電気工事士学科試験で出題されている「三相誘導電動機のスターデルタ始動法」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ三相誘導電動機を逆回転させる方法: 第二種電気工事士学科試験で出題されている「三相誘導電動機を逆回転させる方法」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ三相誘導電動機の力率改善: 第二種電気工事士学科試験で出題されている「三相誘導電動機の力率改善」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ計器に表示されている記号: 第二種電気工事士学科試験で出題されている「計器に表示されている記号」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ電圧、電流、電力、力率の測定回路: 第二種電気工事士学科試験で出題されている「電圧、電流、電力、力率の測定回路」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズクランプ形の電流計による電流の測定: 第二種電気工事士学科試験で出題されている「クランプ形の電流計による電流の測定」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ接地抵抗計と接地抵抗の測定方法: 第二種電気工事士学科試験で出題されている「接地抵抗計と接地抵抗の測定方法」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ絶縁抵抗計と絶縁抵抗の測定: 第二種電気工事士学科試験で出題されている「絶縁抵抗計と絶縁抵抗の測定」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ回路計（テスタ）: 第二種電気工事士学科試験で出題されている「回路計（テスタ）」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ検電器: 第二種電気工事士学科試験で出題されている「検電器」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ竣工検査: 第二種電気工事士学科試験で出題されている「竣工検査」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ電気設備技術基準・解釈: 第二種電気工事士学科試験で出題されている「電気設備技術基準・解釈」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ電気事業法: 第二種電気工事士学科試験で出題されている「電気事業法」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ電気工事士法: 第二種電気工事士学科試験で出題されている「電気工事士法」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ電気工事業法: 第二種電気工事士学科試験で出題されている「電気工事業法（電気工事業の業務の適正化に関する法律）」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ電気用品安全法: 第二種電気工事士学科試験で出題されている「電気用品安全法」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ電線の許容電流: 第二種電気工事士学科試験で出題されている「電線の許容電流」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ分岐回路の開閉器および過電流遮断器の施設: 第二種電気工事士学科試験で出題されている「分岐回路の開閉器および過電流遮断器の施設」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ配線の図記号: 第二種電気工事士学科試験で出題されている「配線の図記号」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ絶縁電線・ケーブルの記号: 第二種電気工事士学科試験で出題されている「絶縁電線・ケーブルの記号」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ電線管・ダクトの記号: 第二種電気工事士学科試験で出題されている「電線管・ダクトの記号」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズスイッチの図記号: 第二種電気工事士学科試験で出題されている「スイッチの図記号」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズコンセントの図記号: 第二種電気工事士学科試験で出題されている「コンセントの図記号」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ遮断器と開閉器の図記号: 第二種電気工事士学科試験で出題されている「遮断器と開閉器の図記号」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ照明器具の図記号: 第二種電気工事士学科試験で出題されている「照明器具の図記号」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ電気機器・計器の図記号: 第二種電気工事士学科試験で出題されている「電気機器・計器の図記号」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズボックスなどその他の図記号: 第二種電気工事士学科試験で出題されている「ボックスなどその他の図記号」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズコンセントの刃受の形状（極配置）: 第二種電気工事士学科試験で出題されている「コンセントの刃受の形状（極配置）」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ最少電線本数（心線数）: 第二種電気工事士学科試験で出題されている「最少電線本数（心線数）」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ配線工事に必要なケーブル: 第二種電気工事士学科試験で出題されている「配線工事に必要なケーブル」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズ差込形コネクタの種類と最少個数の組合せ: 第二種電気工事士学科試験で出題されている「使用する差込形コネクタの種類と最少個数の組合せ」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズリングスリーブの種類と最少個数の組合せ: 第二種電気工事士学科試験で出題されている「使用するリングスリーブの種類と最少個数の組合せ」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
4択クイズリングスリーブの種類、個数、刻印の組合せ: 第二種電気工事士学科試験で出題されている「使用するリングスリーブの種類、個数および刻印の組合せ」について4択クイズ（一問一答）にしてみました。スマホでもできるので（たぶん）、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。

第二種電気工事士｜学科試験対策｜4択クイズ｜幹線の太さを決める根拠となる電流の最小値