スポンサーリンク
幹線の太さを決める根拠となる電流の最小値(電技解釈第148条)
※ページ内にPR・広告が含まれる場合があります。
幹線の太さを決める根拠となる電流の最小値を求める問題は、第二種電気工事士学科試験でよく出題されています。
幹線について
まず初めに、幹線について説明します。
幹線とは、いろいろな負荷に電力(電気)を供給するための大元の配線と考えておけばいいです。例えば、次の図のようなイメージです。
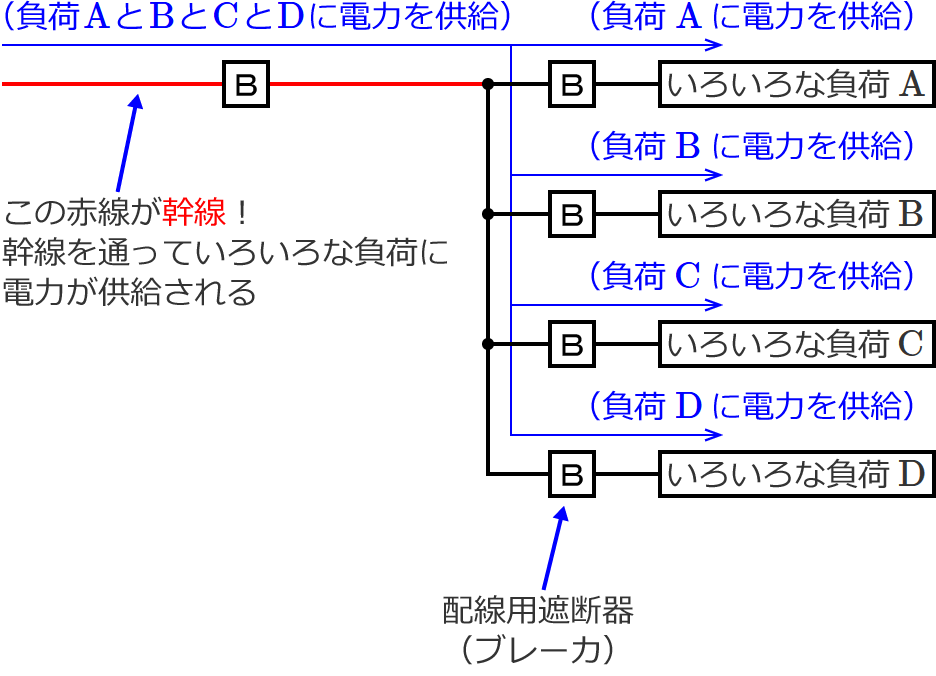
上図をみると、図の赤色の配線を通っていろいろな負荷 $\mathrm{A}$、$\mathrm{B}$、$\mathrm{C}$、$\mathrm{D}$ に電力が供給されていますが、この大元の配線(赤色の線で書いてあるところ)のことを幹線といいます。
この幹線には負荷 $\mathrm{A}$、$\mathrm{B}$、$\mathrm{C}$、$\mathrm{D}$ に供給する分の電流が流れるので、
幹線には大きな電流が流れる
場合があります。
電力・電力量・発熱量のページの発熱量のところで解説したように、電流が流れると抵抗(この場合、配線)に熱が発生し、抵抗が大きければ大きいほど、また、電流が大きければ大きいほど発生する熱も大きくなります。
したがって、大きな電流が流れる場合がある幹線の太さを細くすると、幹線(配線)からの発熱が大きくなって、安全に電気(電流)を流せなくなる場合があります。なので、幹線に電流がどのくらい流れるかを計算し、その値から幹線の太さを決める必要があるんです。
電線の太さが細くなればなるほど電線の抵抗は大きくなり、電線の太さが太くなればなるほど電線の抵抗は小さくなります。電線の太さと電線の抵抗の関係については、こちらの電線の抵抗のページを参考にしてみてください。
スポンサーリンク
スポンサーリンク
幹線の太さを決める根拠となる電流の最小値の求め方
それでは本題で、幹線の太さを決める根拠となる電流の最小値の求め方について説明します。
次のように、幹線があって、その幹線に次のような4つの負荷が接続されているとします。

上図の負荷 $\mathrm{M_1}$ と $\mathrm{M_2}$ は「電動機など始動電流が大きい負荷」、$\mathrm{H_1}$ と $\mathrm{H_2}$ は「その他の負荷(=始動電流が大きくない負荷)」です。
ここで、「始動電流が大きい」とか「始動電流が大きくない」という言葉がでてきましたが、始動電流が大きい負荷というのは負荷に電源が入ったときに、
瞬間的にドーンと大きな電流が流れる負荷
のことで、その代表的なものが電動機になります。
第二種電気工事士学科試験では、
「始動電流が大きい負荷」= 電動機
「始動電流が大きくない負荷(その他の負荷)」= 電動機以外(電熱器など)
とおぼえておけばいいと思います。
それで、幹線の太さを決める根拠となる電流の最小値の求め方ですが、説明のために各負荷の定格電流、幹線の許容電流などを次のように定義します。
$I_W$:幹線の太さを決める許容電流(これが求める電流の最小値)
$I_{M1}$:電動機など始動電流が大きい負荷 $\mathrm{M_1}$ の定格電流
$I_{M2}$:電動機など始動電流が大きい負荷 $\mathrm{M_2}$ の定格電流
$I_M$:電動機など始動電流が大きい負荷の定格電流の合計(この場合、$I_{M1}$ と $I_{M2}$ を足した値)
$I_{H1}$:始動電流が大きくない負荷 $\mathrm{H_1}$ の定格電流
$I_{H2}$:始動電流が大きくない負荷 $\mathrm{H_2}$ の定格電流
$I_H$:始動電流が大きくない負荷の定格電流の合計(この場合、$I_{H1}$ と $I_{H2}$ を足した値)
イメージしやすいように図で書くと次のようになります。
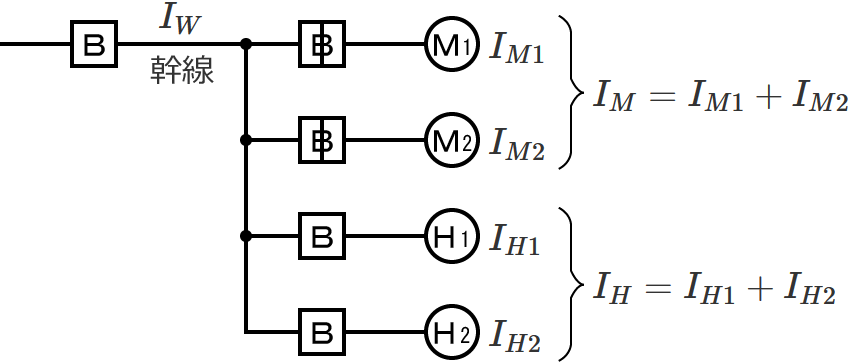
すると、幹線の太さを決める根拠となる電流の最小値を求める手順は、次のようになります。
手順①
電動機など始動電流が大きい負荷の定格電流の合計 $I_M$ 、始動電流が大きくない負荷(その他の負荷)の定格電流の合計 $I_H$ をそれぞれ求めます。(この場合は、$I_M=I_{M1}+I_{M2}$ 、$I_H=I_{H1}+I_{H2}$ )
手順②
手順①で求めた $I_H$ と $I_M$ を比較し、$I_H\geqq I_M$ の場合は手順③へ、$I_H\lt I_M$ の場合は手順④へ。
手順③
$I_H\geqq I_M$ の場合は、次の式で幹線の太さを決める根拠となる電流の最小値を求めます。
$\therefore I_W\geqq I_M+I_H$ ($I_M$ と $I_H$ を足すだけ)
手順④
$I_H\lt I_M$ の場合は、次の($\mathrm{A}$)式または($\mathrm{B}$)式で幹線の太さを決める根拠となる電流の最小値を求めます。($I_M\gt 50\,\mathrm{A}$ のときは($\mathrm{A}$)式を使い、$I_M\leqq 50\,\mathrm{A}$ のときは($\mathrm{B}$)式を使う。)
$I_H\lt I_M$ で、$I_M\gt 50\,\mathrm{A}$ のとき、
$\therefore I_W\geqq 1.1\times I_M+I_H$ …($\mathrm{A}$) ($I_M$ を $1.1$ 倍して $I_H$ を足す)
$I_H\lt I_M$ で、$I_M\leqq 50\,\mathrm{A}$ のとき、
$\therefore I_W\geqq 1.25\times I_M+I_H$ …($\mathrm{B}$) ($I_M$ を $1.25$ 倍して $I_H$ を足す)
$I_H\lt I_M$ の場合は、$I_M$ の大きさで式を使い分けるのでちょっとめんどうですね…。
幹線の太さを決める根拠となる電流の最小値を求める手順を図にまとめると、次のようになります。幹線の太さを決める根拠となる電流の最小値を求める問題は、この図をおぼえておけば大丈夫です!(たぶん)

需要率をかける
問題に示されている需要率が $100\,\%$ ではない場合には、それぞれの定格電流に需要率をかけ、その値を使って計算します。(例:需要率が $80\,\%$ の場合は、それぞれの定格電流に $0.8$ をかけます。)
以上が、幹線の太さを決める根拠となる電流の最小値の求め方になります。
スポンサーリンク
スポンサーリンク
このページを読んだら、4択クイズをやってみよう!
幹線の太さを決める根拠となる電流の最小値の4択クイズはこちら ⇒ 第二種電気工事士学科試験の4択クイズ 幹線の太さを決める根拠となる電流の最小値
配線用遮断器の動作時間(電技解釈第33条) ←BACK
スポンサーリンク
幹線の太さを決める根拠となる電流の最小値(電技解釈第148条) 関連ページ
- 電線の許容電流(電技解釈第146条)
- 第二種電気工事士学科試験の「配線設計」分野で出題される電線の許容電流について、解き方のポイントをまとめています。電線の許容電流(電技解釈第146条)に関する問題はほぼ毎年(毎回)出題されますので、ここで解き方のポイントをおさえておきましょう。
- 配線用遮断器の動作時間(電技解釈第33条)
- 第二種電気工事士学科試験の「配線設計」分野で出題される配線用遮断器の動作時間についてまとめています。配線用遮断器の動作時間(電技解釈第33条)に関する問題は学科試験でときどき出題されるのでおぼえておくようにしましょう。
- 分岐回路の開閉器および過電流遮断器の施設(電技解釈第149条)
- 第二種電気工事士学科試験で出題される「分岐回路の開閉器および過電流遮断器の施設」についてまとめています。分岐回路の開閉器と過電流遮断器はどの位置(箇所)に施設しなければならないかは、電技解釈第149条で規定されています。第二種電気工事士の学科試験でも度々出題される範囲ですので、しっかりとおぼえておきましょう。
- 分岐回路の電線の太さと接続できるコンセント(電技解釈第149条)
- 第二種電気工事士学科試験で出題される「分岐回路の電線の太さと接続できるコンセント」についてまとめています。分岐回路を保護する過電流遮断器または配線用遮断器の定格電流、電線の太さにより接続できるコンセントの定格電流が決まります。


